不同参照系里的功能关系

孙梦家

(景德镇一中，江西 景德镇 333000)

功能关系是中学物理乃至整个普通物理学中非常重要的关系。不论功还是能都和物体的运动有关，而物体的运动又和参照系的选取有关，那么功和能与参照系的选取有什么样的关系?

1 问题提出

某人在以速度v行驶的大船上先后以速率u(相对于船)向船头和船尾方向投出质量m的球。试问，在两次投球中，他做的功是否相同?

解1:以地面为参照系，向船头投球时，球的动能的增量为:

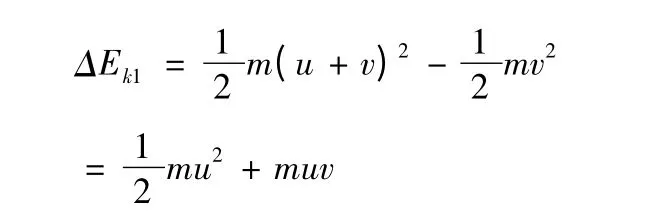
向船尾投球时，球的动能的增量为:

可见，两次投球动能的增量不同，根据动能定理，两次投球时人做的功也不同。

解2:以船为参照系，两次投球中动能的增量为:

所以，两次投球动能的增量相同，根据动能定理两次投球人做的功也相同。这里，某人所做的功是将人消耗的生物能转化为机械能。按生活常识可知，在两次投球中，人所消耗的生物能应相同，而上面的两种解法的结果却不同，而计算似乎都合理，问题出在哪里呢?实质问题也就是，不同的参照系里的功能关系，即动能定理是否都成立，是否都一样?

2 以地面为参照系研究

原题解法一的结果与实验结果相违背，那么错在哪里呢?问题出在当我们投球的时候，由于质点系(人、船、球组成)的动量守恒，轮船的速度也将发生改变，这变化导致轮船的动能改变，而船的动能改变也应该计算到投球时做的功中去。

在第一种情况下，球向前投，人、球与船组成的质点系的动量守恒即:

式中v'是球投出后船的速度，m是球的质量，M是人和船的质量:

此时球的速度为:

投球时做的功，应为人、球和船的动能之和，即:

在(4)式中前一个方括号为球的动能增量，后一个括号中为人和船的动能增量。

如果人和船的质量远大于球的质量，即时，

在第二种情况下，球向后投时人做的功的计算与上面相似，将u改为－u即可，由(5)式可得:

这结果与第一种情况相同。

通过以上的计算，使我们注意到:投球后，船的速度v'变化为(2)式所示，在M≫m的前提下，只就速度而言，可以略去这一项，即可以认为船的速度不变，但就动能而言，因为要乘上M这一项，它引起人与船的动能变化是相当大的，故不能略去。

3 以轮船为参照系研究

我们注意到，上面的讨论中以地面为参照系的情况下，虽然向前和向后投球人做的功相同，但计算结果与原题解法二给出的结果却不相同，这又是为什么呢?从上面的分析中，我们看到投球后，轮船的速度要改变，从v变为v'，这样它相对地面就不再是匀速直线运动，也就是说，不再是一个惯性参照系，而在非惯性参照系中，要计入惯性力做功，动能定理才能成立。我们可以选取人、轮船与球的质心为参照系。因为质心以不变的速度v做匀速直线运动。如果船的质量M远大于球的质量m，人、轮船与球的质心近似为人、船的质心。选质心参照系就是近似选人、轮船为参照系。所以以相对于船速度为u投球，不论是向前还是向后，所做的功都是近似成立条件是M≫m，这样结果就与上面以地面为参照系求出的结果一样了。如果不满足M≫m的条件，就不能选人、轮船为参照系，而应严格地选地面或质心参照系来计算投球时做的功。

4 不同参照系中的功和能

4.1 动能定理

若以地面为参照系:设有一质点m，受力F作用，在力的方向上移动了一段距离S，v0是质点的初速度，v是质点的末速度。

现在以另一个惯性参照系来观察这个质点的运动，比如是在地面上以速度u匀速运动的汽车，以汽车为参照系。在汽车参照系中质点m的位移S'，由伽利略变换S'=s－ut。质点的初末动能分别为

在质心系中:

在质心系中人向前和向后投球时所做的功:

可见在不同惯性系中动能定理都是成立的。但是，在不同惯性系中动能的变化及力所做的功可以不同，因为在不同参照系的位移也可以不同。

4.2 质心参考系

根据柯尼希定理，质点系对惯性系的动能等于质点系对质心系的动能与质心对惯性系的动能之和。

设有m1，m2有组成的系统，m1，m2对地面参照系的速度分别为v1和v2，两速度在同一直线上，则质心的速度:

设E'k为质点系在质心系中的动能，Ek为质点系对惯性系的动能，Ekc为质心对惯性系的动能:

通过比较可知，在地面参照系中和质心系中人所做的功是一样的。