矩形油藏多段压裂水平井不稳态压力分析
王晓冬,罗万静,侯晓春,王军磊
(1. 中国地质大学(北京);2. 中国石油勘探开发研究院)
矩形油藏多段压裂水平井不稳态压力分析
王晓冬1,罗万静1,侯晓春1,王军磊2
(1. 中国地质大学(北京);2. 中国石油勘探开发研究院)
通过确定导流能力影响函数,给出了有限导流垂直裂缝井不稳定渗流的新解析解。再利用叠加原理得到了带有多条有限导流垂直裂缝的压裂水平井不稳定压力分布。计算结果表明,理想模式下渗流方式发生的顺序是早期双线性流动→早期线性流动→中期径向流动→中期线性流动→晚期拟稳态流动;均匀分布等导流裂缝缝长的不均匀性主要影响早期双线性流动和线性流动阶段的转换时期,加快中期径向流动的出现;等长等导流裂缝分布的不对称性主要影响中期线性流动阶段,不对称性越强,受矩形地层各条边界的影响越明显;等长均布裂缝导流能力的强弱主要影响早期双线性流动和线性流动阶段,导流能力的差异使得早期双线性流动持续时间变短而线性流动持续时间相对增加;等长等导流均布裂缝条数增加,储集层整体压力降落加快,中期径向流段持续时间变短而中期线性流段延长,而裂缝长度相对增加,中期径向流段持续时间变短而中期线性流段可能不出现,说明压裂水平井具分段改善渗流方式的特点。图8参19
多段压裂水平井;有限导流垂直裂缝;不稳态压力分析;流动段;矩形油藏
0 引言
压裂水平井通过选择性地分段建立水力裂缝,将近井筒地层中的渗流方式由平面径向流动改变为平面线性流动,由此提高开采过程中地层能量的利用率,扩大动用面积。随着压裂工艺的进步,压裂水平井在中国开采致密油气方面应用前景广泛[1-4]。
压裂水平井的动态分析难点主要在于合理描述多裂缝间的相互干扰以及与地层流动相耦合的横切裂缝(Transverse Fracture)导流影响。在多裂缝干扰方面,Larsen和Hegre[5-6]首先给出了三维无界地层中带有多条圆形有限导流裂缝的压裂水平井不稳态渗流解析解,结果只是比较好地展现了系统早、中期阶段的渗流特征;Guo和Evans[7]给出了一种平面无界地层中带有多条无限导流等长垂直裂缝的压裂水平井不稳态渗流实时域解析解,由于边部裂缝和内部裂缝控制的泄流面积不同,其直接叠加的解式不很严格;Horne和Temeng[8]虽然改进了Guo和Evans模型对缝间干扰考虑的不足,但依然没有考虑裂缝导流的影响。在裂缝导流影响方面,Chen和Raghavan[9]在Laplace变换域中给出了平面无界地层中带有多条有限导流均匀分布垂直裂缝的压裂水平井不稳态渗流解析解,由于采用边界元方法求解有限导流裂缝模型,当裂缝条数比较多时计算速度不佳;Al-Kobaisi和Ozkan等[10]建立了一种解析-数值混合网格模型(用解析解表述地层渗流,用差分模型描述裂缝流动),Valkó和Amini[11]提出了一种DVS(Distributed Volumetric Sources)方法,采用数值离散法描述裂缝导流的影响,较为复杂;Brown和Ozkan等人[12]以及Stalgorova和Mattar[13]将有限导流垂直裂缝之三线性流动模型用于多段压裂水平井动态分析中,虽然能够避免数值求解裂缝流动模型,却不能得到中期径向流动特征。
综上所述,多裂缝间相互干扰问题可通过多井叠加原理解决,而横切裂缝导流和聚流的影响问题,主要有4种处理方式:①采用无限导流假设,不考虑裂缝导流影响,只是附加聚流表皮;②采用经典的边界元方法求解有限导流裂缝的耦合积分方程,再附加聚流表皮;③采用有限差分或者DVS等数值方法求解有限导流裂缝的耦合积分方程;④采用三线性流动模型。
本文采用多井叠加原理解决多裂缝间相互干扰问题,对于横切裂缝导流影响问题则给出一种新的解决方法,即在无限导流垂直裂缝模型上叠加导流能力影响函数并辅以聚流表皮模型,给出了导流能力影响函数的解析解,并计算了定井流量条件下压裂水平井的压力动态特征。
1 单一有限导流垂直裂缝压力分布
在长为xe、宽为ye、高为h(油层厚度)的箱形封闭均质地层中有一压裂水平井(见图1)。首先考察在某位置处产生一条板状横切垂直裂缝情形(见图1中第1条裂缝),裂缝的高度等于储集层厚度。若裂缝产出微可压缩牛顿流体(流量为qref),则地层中产生不稳态Darcy渗流。将裂缝中的流动分解为线性流动和径向流动2部分,其导流影响可以用普通垂直裂缝井模型再附加聚流表皮来表述[14]。
定义无量纲压力、无量纲时间、无量纲导流能力和裂缝无量纲生产指数为:
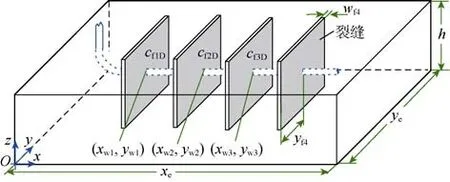
图1 压裂水平井示意图
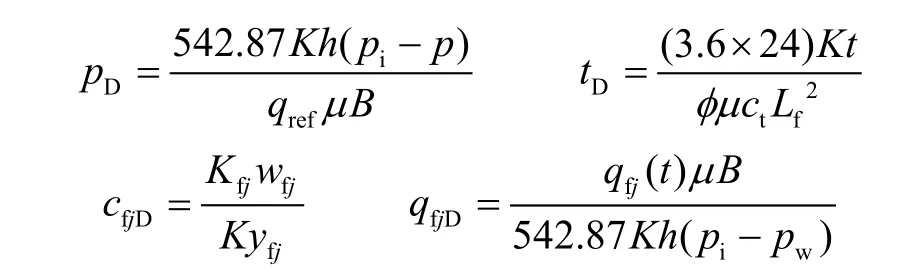
其他无量纲量为:
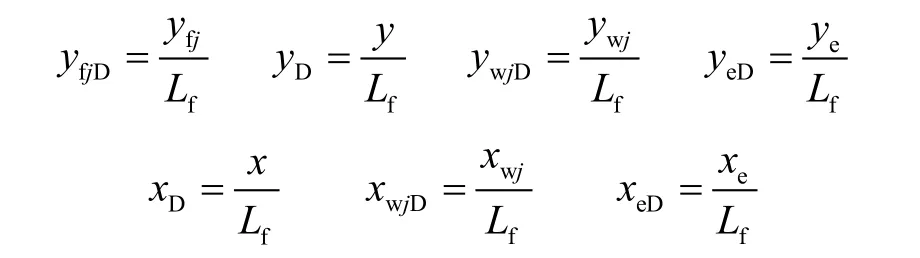
对于单一无限导流垂直裂缝情形,通过Green函数求解和Laplace变换,其压力分布为[15]:
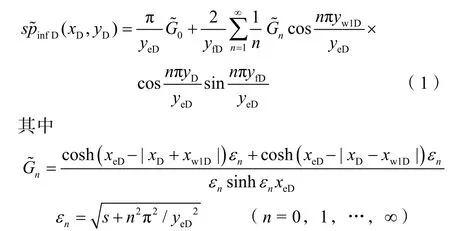
上式中s为Laplace变量,上标“~”为Laplace变换量。对于单一有限导流垂直裂缝情形,压力分布可以写为:
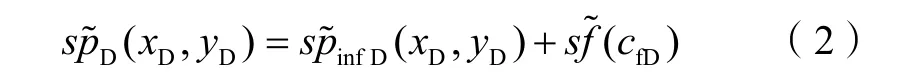
基于Riley等[16]的结果,本文提出导流能力影响函数f (cfD)为:
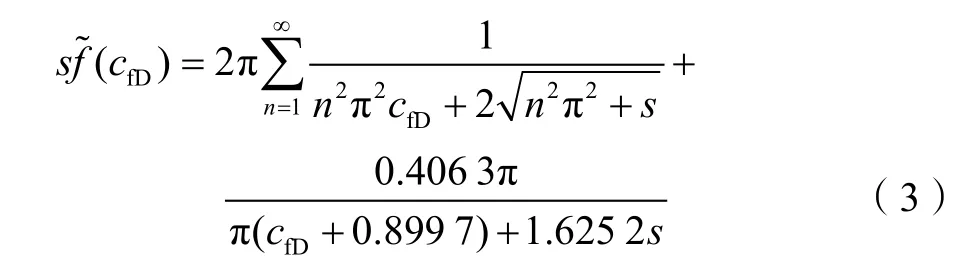
Cinco-Ley等[17]采用有限差分、Cinco-Ley和Meng[18]采用边界元方法数值计算裂缝导流模型得到有限导流裂缝的井底压力,本文则通过(2)式得到相应结果,对比结果见图2。
图2表明,采用(2)式计算垂直裂缝导流的影响完全可行,这一结果比Cossio等人[19]的分区分形近似模型要简单实用。显然,利用(2)式计算压裂水平井的横切裂缝问题还需要加入聚流表皮因子Sc[14]:
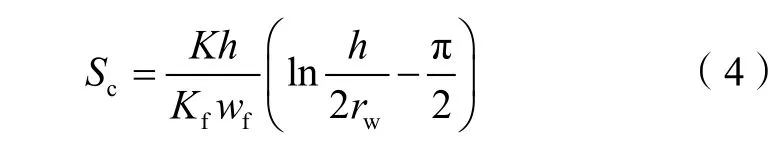
由(4)式可见,对于给定的储集层,聚流表皮的影响与裂缝导流能力(Kfwf)成反比关系。对于给定的裂缝,聚流表皮因子是常值,它只产生附加压降,不影响流动期表现特征。
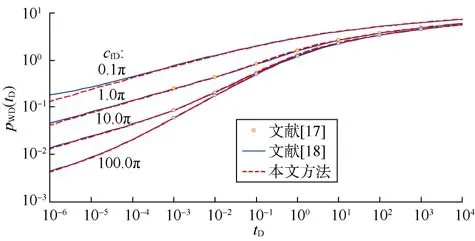
图2 有限导流垂直裂缝无量纲井底压力计算对比
2 多段压裂水平井不稳态渗流模型
若分段压裂水平井产生N条裂缝,当N条裂缝同时工作,在储集层任意位置处产生的无量纲压降等于单个裂缝独自工作产生的无量纲压降之代数和。由于每条裂缝的总流量是时间的函数,根据Duhamel褶积,在Laplace变换域中有:
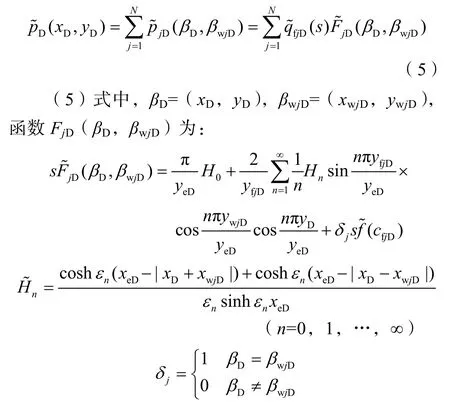
若井定流量生产,忽略沿水平井筒压力损失,每条裂缝的流压近似相同,且等于井底流压,则有如下线性方程组:
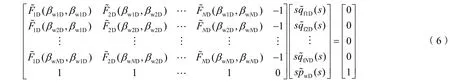
求解(6)式,可以同时得到井定流量生产情形下每条裂缝瞬时流量和井底压力,以下主要讨论井底压力表现特征。
3 压力动态特征
压裂水平井不稳态压力特征的主要影响因素有裂缝条数、位置分布、长度分布以及导流能力。由于影响因素较多,本文首先建立一种理想模式(泄流区中心位置布置等长均布等导流裂缝模型),然后相对改变单因素进行计算和对比分析,以便把握各个参数的影响特征。
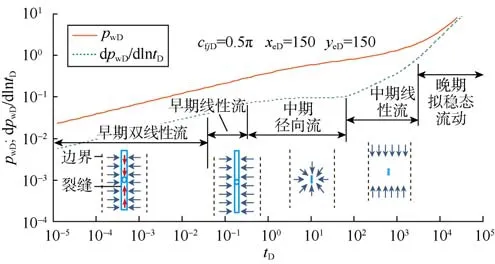
图3 对称均匀分布5条等长等导流裂缝压裂水平井井底压力和压力导数曲线
3.1 对称均匀分布5条等长等导流裂缝
裂缝对称均匀等长分布为一种理想模式,即处于中心地带的N条裂缝等长均匀分布,具有相同导流能力的各条裂缝(包括边部裂缝)占有相同的子泄流面积(子泄流面积等于总泄流面积的1/N)。由于2条裂缝间产生分流线,井底压力表现将与相应的单条裂缝行为一致(单条裂缝位于各自占据的泄流面积内,流量为井流量的1/N)。这一特例与Guo和Evans[7]的解析解式一致,反映了多段压裂水平井压力诊断曲线的基本特征(见图3),渗流方式发生的顺序是:早期双线性流动(裂缝+近井地层)→早期线性流动(近井地层)→中期径向流动(地层)→中期线性流动(远井地层)→晚期拟稳态流动(封闭边界影响)。受裂缝导流能力和相对位置等影响,某些情况下部分流动方式的特征可能不明显。
3.2 对称均匀分布5条不等长等导流裂缝
若裂缝分布均匀,但各裂缝长度不等,其井底压力表现形态见图4。对比等长情形(见图4模型1)可知,裂缝长度的不均匀性主要影响早期双线性流动和线性流动的转换时期,加快中期径向流动的出现,而对中期线性流动和晚期拟稳态流动影响较弱。
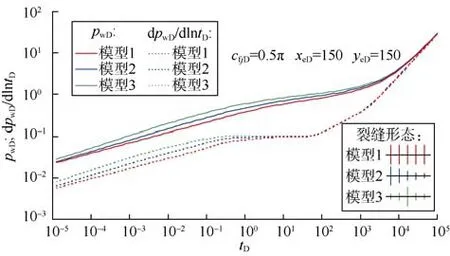
图4 对称均匀分布5条不等长等导流裂缝压裂水平井井底压力和压力导数曲线
3.3 不对称均匀分布5条等长等导流裂缝
若等长裂缝分布不对称,其井底压力表现形态见图5。图5表明,等长裂缝分布的不对称性主要影响中期线性流动阶段,类似于偏心的单条垂直裂缝情形,对比等长情形(见图5模型1)可知,随着裂缝分布不对称性增强,矩形地层各条边界的影响有可能分期而至,有可能掩盖中期径向流动而直接出现半径向流或者中期线性流动,最后归结为拟稳态流动。
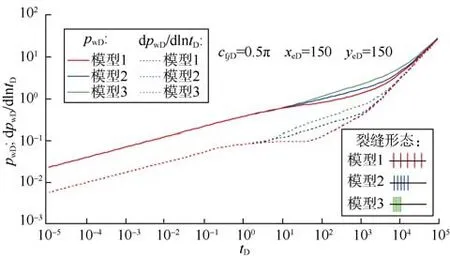
图5 不对称均匀分布5条等长等导流裂缝压裂水平井井底压力和压力导数曲线
3.4 对称均匀分布多条等长等导流裂缝
若对称等长均布裂缝条数增加,其井底压力表现形态见图6。图6表明,等长均布裂缝条数主要影响早期双线性流动、线性流动和中期径向流动阶段。与单条裂缝情形(见图6模型1)相比,裂缝条数的增加将使储集层整体压力降落加快,无量纲压力变小,压力导数水平段(中期径向流段)下降至0.5/N位置,中期径向流段持续时间变短而中期线性流段增长,体现了压裂水平井分段改善渗流方式的特点,能够提高开采过程中地层能量的利用率。
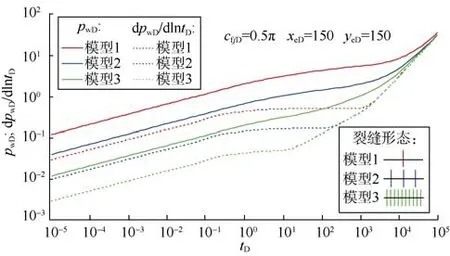
图6 对称均匀分布多条等长等导流裂缝压裂水平井井底压力和压力导数曲线
3.5 对称均匀分布5条等长不等导流裂缝
若等长均布裂缝导流能力各有差异,其井底压力表现形态见图7。图7表明,等长均布裂缝导流能力差异主要影响前期双线性流动和线性流动阶段,与导流能力一致情形(见图7模型1)相比,导流能力的差异使得早期双线性流动过早转化为线性流动,即双线性流动持续时间变短而线性流动持续时间增加。
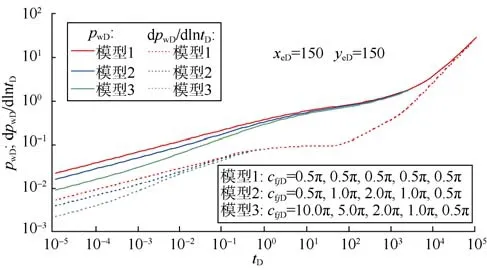
图7 对称均匀分布等长5条不等导流裂缝压裂水平井井底压力和压力导数曲线
3.6 对称均匀分布5条等导流裂缝长度变化
若等长均布、等导流裂缝长度增加,其井底压力表现形态见图8。图8表明,裂缝长度增加,等效于矩形储集层垂直于裂缝方向(y方向)的边界缩小,主要影响中期径向流动阶段持续时间、中期线性流段持续时间和晚期拟稳态流动出现时间,比较而言,长裂缝使得储集层中早期双线性流、线性流动段相对加长,而中期径向流段持续时间变短,甚至于出现短暂中期径向流动而不出现中期线性流动,这也体现了压裂水平井分段改善渗流方式的特点。
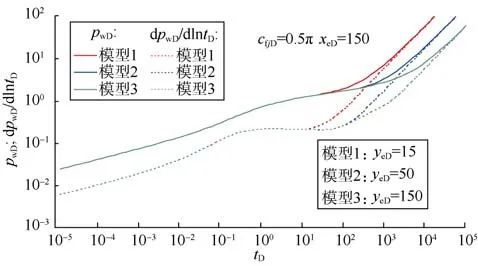
图8 对称均匀分布5条等导流裂缝长度变化压裂水平井井底压力和压力导数曲线
由于本文给出的是Laplace变换解,根据Duhamel褶积很容易得到考虑井筒存储和表皮效应的不稳定试井压力诊断曲线,井筒存储效应主要使早期的双线性流动和线性流动阶段滞后出现,而早期压力和压力导数产生单位斜率直线段,限于篇幅,本文不再赘述。
4 结论
多段压裂水平井压力动态分析的主要难点在于合理描述多裂缝间的相互干扰以及与地层流动相耦合的横切裂缝导流和聚流影响。基于前人数学模型的特点和不足,提出无限导流垂直裂缝模型叠加导流能力影响函数的新方法,给出了导流能力影响函数的解析解,计算对比表明,本文方法便捷准确。
建立了矩形地层中心地带多条等长均匀分布、等导流裂缝理想模式,每条裂缝占有相同的子泄流面积;在理想模式下,生产井的井底压力表现与相应的单条裂缝行为一致,指明了不稳定渗流过程中渗流方式发生的次序和井底压力导数特征。
与理想模式相比,均匀分布、等导流裂缝的缝长的参差不齐,主要影响井底压力早期双线性流动和线性流动阶段的转换时期,加快中期径向流动的出现;而等长、等导流裂缝分布的不对称性主要影响中期线性流动阶段,不均匀性越强,受矩形地层各条边界的影响越明显,有可能掩盖中期径向流动而直接出现半径向流或者中期线性流动等;等长均布裂缝导流能力的强弱主要影响早期双线性流动和线性流动阶段,导流能力的差异使得早期双线性流动过早转化为线性流动,即双线性流动持续时间变短而线性流动持续时间相对增加。
若等长、等导流均布裂缝条数增加,将使得储集层整体压力降落加快,中期径向流段持续时间变短而中期线性流动段延长;若等长、等导流均布裂缝之裂缝长度相对增加,中期径向流段持续时间变短而中期线性流动段可能不出现,体现了压裂水平井分段改善渗流方式的特点。
本文旨在阐述不稳态压力的流动期特征,由于给出的是Laplace变换解式,用于指导不稳定试井分析,结果很容易扩展得到包含井筒存储效应和表皮效应的压力诊断曲线。
符号注释:
x、y——平面坐标;wf——填砂裂缝宽度,m;yf——裂缝半长,m;p——压力,MPa;pi——地层静压,MPa;pw——井底流压,MPa;K——地层渗透率,μm2;Kf——填砂裂缝渗透率,μm2;h——储集层厚度,m;μ——流体黏度,mPa·s;B——流体体积系数,m3/m3;φ——储集层孔隙度,f;t——延续时间,d;ct——综合压缩系数,MPa-1;Lf——特征长度,m,可取所有水力裂缝中的最大半长;cf——裂缝导流能力,10-3μm2·cm;qref——特征流量,m3/d;qf——裂缝流量,m3/d;xwj——第j条裂缝横坐标位置,m;ywj——第j条裂缝纵坐标位置,m;xe——储集层横向边界,m;ye——储集层纵向边界,m;pinfD——单一无限导流垂直裂缝无量纲压力分布;n——求和中的枚举变量;Sc——聚流表皮因子,无量纲;rw——井筒半径,m;N——总裂缝条数。下标:D——无量纲;j——裂缝序号。
[1] 何东博, 贾爱林, 冀光, 等. 苏里格大型致密砂岩气田开发井型井网技术[J]. 石油勘探与开发, 2013, 40(1): 79-89.
He Dongbo, Jia Ailin, Ji Guang, et al. Well type and pattern optimization technology for large scale tight sand gas, Sulige gas field[J]. Petroleum Exploration and Development, 2013, 40(1): 79-89.
[2] 侯向前, 卢拥军, 方波, 等. 非常规储集层低碳烃无水压裂液[J].石油勘探与开发, 2013, 40(5): 601-605.
Hou Xiangqian, Lu Yongjun, Fang Bo, et al. Waterless fracturing fluid with low carbon hydrocarbon as base fluid for unconventional reservoirs[J]. Petroleum Exploration and Development, 2013, 40(5): 601-605.
[3] 黄昌武. 页岩油气压裂理论方法和技术体系初步形成[J]. 石油勘探与开发, 2012, 39(4): 443.
Huang Changwu. Theoretical methodology and technical system for shale reservoir fracturing[J]. Petroleum Exploration and Development, 2012, 39(4): 443.
[4] 马新华, 贾爱林, 谭健, 等. 中国致密砂岩气开发工程技术与实践[J]. 石油勘探与开发, 2012, 39(5): 572-579.
Ma Xinhua, Jia Ailin, Tan Jian, et al. Tight sand gas development technologies and practices in China[J]. Petroleum Exploration and Development, 2012, 39(5): 572-579.
[5] Larsen L, Hegre T M. Pressure-transient behavior of horizontal wells with finite-conductivity vertical fractures[R]. SPE 22076, 1991.
[6] Larsen L, Hegre T M. Pressure transient analysis of multifractured horizontal wells[R]. SPE 28389, 1994.
[7] Guo G, Evans R D. Pressure-transient behavior and inflow performance of horizontal wells intersecting discrete fractures[R]. SPE 26446, 1993.
[8] Horne R N, Temeng K O. Relative productivities and pressure transient modeling of horizontal wells with multiple fractures[R]. SPE 29891, 1995.
[9] Chen C C, Raghavan R. A multi-fractured horizontal well in a rectangular drainage region[R]. SPE 37072, 1996.
[10] Al-Kobaisi M, Ozkan E, Kazemi H. A hybrid numerical/analytical model of finite-conductivity vertical fracture intercepted by a horizontal well[R]. SPE 92040, 2006.
[11] Valkó P P, Amini S. The method of distributed volumetric sources for calculating the transient and pseudosteady-state productivity of complex well-fracture configurations[R]. SPE 106279, 2007.
[12] Brown M, Ozkan E, Raghavan R. Practical solutions for pressure transient responses of fractured horizontal wells in unconventional reservoirs[R]. SPE 125043, 2009.
[13] Stalgorova E, Mattar L. Practical analytical model to simulate production of horizontal wells with branch fractures[R]. SPE 162515-MS, 2012.
[14] Mukherjee H, Economies M J. A parametric comparison of horizontal and vertical well performance[R]. SPE 18303, 1991.
[15] Ozkan E, Raghavan R. New solutions for well-test-analysis problems: part 1: Analytical considerations[R]. SPE 18615, 1991.
[16] Riley M F, Brigham W E, Horne R N. Analytical solutions for elliptical finite-conductivity fractures[R]. SPE 22656, 1991.
[17] Cinco-Ley H, Samaniego V F, Dominguez A N. Transient pressure behavior for a well with a finite-conductivity vertical fracture[R]. SPE 6014, 1976.
[18] Cinco-Ley H, Meng H Z. Pressure transient analysis of wells with finite conductivity vertical fractures in double porosity reservoirs[R]. SPE 18172-MS, 1988.
[19] Cossio M, Moridis G J, Blasingame T A. A semi-analytic solution for flow in finite-conductivity vertical fractures using fractal theory[R]. SPE 153715, 2012.
Transient pressure analysis of multiple-fractured horizontal wells in boxed reservoirs
Wang Xiaodong1, Luo Wanjing1, Hou Xiaochun1, Wang Junlei2
(1. China University of Geosciences, Beijing 100083, China; 2. PetroChina Research Institute of Petroleum Exploration & Development, Beijing 100083, China)
A new analytical solution of fluid unsteady flow was presented for wells with finite-conductivity vertical fractures by determining impact functions of fracture conductivity. Based on the new solution, the transient pressure distribution of a fractured horizontal well with multiple finite-conductivity vertical fractures was obtained using the principle of superposition. Calculation results show the pressure transient behavior of fractured horizontal wells under the condition of constant bottom rate. In the ideal fracture arrangement, flow patterns occur in the order of early bilinear flow → early linear flow → middle radial flow → middle linear flow→ late pseudo steady state. Uneven length of fractures with equal conductivity and uniform arrangement may affect the transform of early linear flows from earlier bilinear flows and the premature birth of middle radial flows. Nonuniform arrangement of fractures with even length and equal conductivity may influence middle radial flows. Different conductivity of fractures with equal length and uniform arrangement shortens the period of bilinear flows and lengthens the linear flows. Increase in the number of fractures with even length, equal conductivity and uniform arrangement accelerates pressure drops in the reservoir, shortens the period of middle radial flows and lengthens the middle linear flows. Increase in length of all fractures shortens the period of middle radial flows and may result in absence of radial flows. It is demonstrated that the horizontal well with multiple vertical fractures may improve fluid flow patterns.
multiple-fractured horizontal well; vertical fracture with finite conductivity; transient pressure analysis; flow regimes; boxed reservoir
TE355.6; 357.14
A
王晓冬(1963-),男,黑龙江延寿人,中国地质大学(北京)能源学院教授,博士生导师,主要从事油藏工程、油气渗流力学、储集层建模与油藏数值模拟等方面的教学和科研工作。地址:北京市海淀区学院路29号,中国地质大学(北京)能源学院,邮政编码:100083。E-mail:wxd_cug@cugb.edu.cn
2013-08-20
2013-12-30
(编辑 郭海莉 绘图 刘方方)
1000-0747(2014)01-0074-05
10.11698/PED.2014.01.09
国家科技重大专项(2011ZX05013-002;2011ZX05009-004)

