泰勒公式在高等数学解题中的使用技巧

莫庆美

(贺州学院理学院，广西贺州 542899)

泰勒公式在高等数学解题中的使用技巧

莫庆美

(贺州学院理学院，广西贺州 542899)

泰勒公式是高等数学这门课程中的一个重要公式，它是微分学的基本理论。本文通过泰勒公式在求极限、微分方程求解、广义积分和级数敛散性的判别、高阶导数的计算等方面的应用，拓宽了泰勒公式的应用范围，展现了泰勒公式在高等数学中的重要地位，拓广了高等数学问题的解题方法及技巧。

泰勒公式；极限；微分方程；敛散性；高阶导数

泰勒公式是高等数学中的一个重要公式,也是求解高等数学问题的一个重要工具。然而，在高等数学教材中，一般只讲泰勒公式和几个常用函数的麦克劳林公式，对其在解题中的应用很少介绍。对某些未定式的极限来说，运用泰勒公式比使用洛比达法则更方便。泰勒公式对某些微分方程求解、广义积分和级数敛散性的判别、高阶导数的计算等方面也都有很大的作用。本文通过典型例题，讨论泰勒公式在高等数学解题中的使用技巧。

1 求函数的极限

在求某些分式或者复杂的复合函数的极限时，利用泰勒公式的带皮亚诺型余项把其中的某些项展开，可以较为容易解决。

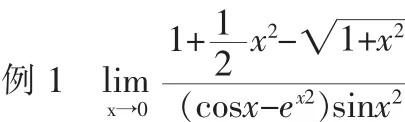
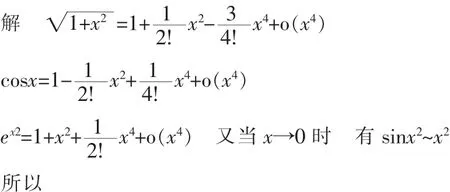
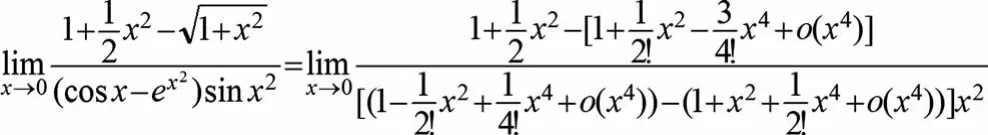
从例1可以看出，利用泰勒展开式代替某些函数时，要考虑分子分母无穷小的阶数，并配合等价无穷小的性质来求极限。

2 求微分方程的解

例2解微分方程xy″-（x+m）y′+my=0(m为自然数)

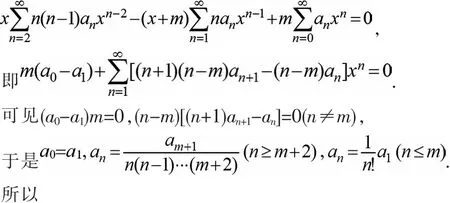
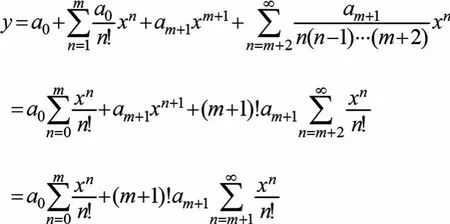
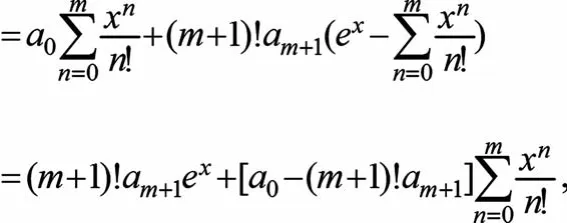
即原方程的通解为

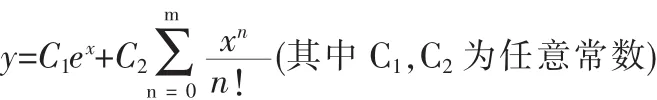
3 判断级数的敛散性

有些复杂的级数用常规的方法很难判别其敛散性，我们可以考虑将其展开成泰勒级数，再进行判定，往往会把问题变得简单。

分析直接通过通项去判断级数是正项级数还是非正项级数比较困难。因而不能直接给出判断级数敛散性的方法。但是我们注意到所给级数通项中的lnn+1=ln（1+1

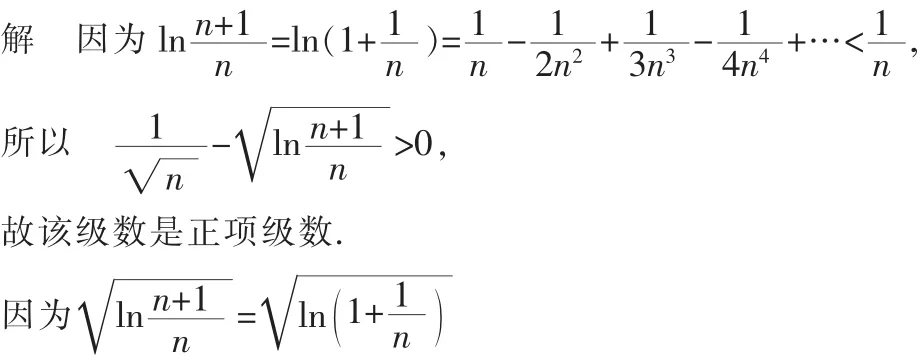
4 判断广义积分的敛散性

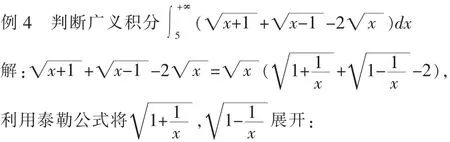
5 求高阶导数在某些点的数值

例设f（x）=x10arctanx，求f（0）（0）

由此可得f（x）的泰勒展开式

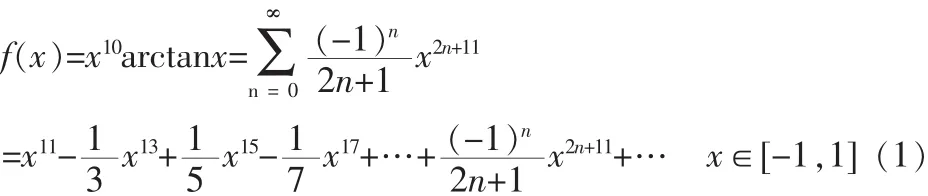
又f（x）在x=0处的麦克劳林展开式为

比较（1）和（2）式中的系数得：

6 结束语

通过上面的几个例子，可以看出利用泰勒公式求解某些函数的极限、求解微分方程、广义积分和级数敛散性的判别、高阶导数的计算具有简洁、方便的作用，从而准确、高效地解决一些数学问题。泰勒公式在五个方面的应用，为解决高等数学问题拓展了思路，从中可以看出泰勒公式在解题中的妙用，对学习和教学都大有脾益。

[1]蔡燧林．常微分方程[M]．杭州：浙江大学出版社，2002．

[2]同济大学数学系．高等数学[M]．北京：高等教育出版社，2007.

[3]华东师范大学数学系．数学分析（3版）[M]．北京：高等教育出版社，2001．

[4]陈丽．泰勒公式的应用[J]．廊坊师范学院学报（自然科学）版，2009，9(2)：20―23．

O171

A

1003-5168(2014)04-0198-02

莫庆美（1963—）,女，汉族，专业副教授，研究方向：高等数学教育教学理论。