奇异双调和方程无穷多解的存在性

戴 琛

(苏州高等幼儿师范学校，江苏苏州 215008)

奇异双调和方程无穷多解的存在性

戴 琛

(苏州高等幼儿师范学校，江苏苏州 215008)

本文利用集中紧性原理和变分方程对奇异双调和方程进行研究，通过截断技术和分析技巧得到了该问题无穷多个解的存在性。

双调和方程；集中紧性原理；变分方法

本文研究如下的奇异双调和方程：

(1)

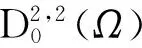
自从Briezis和Nirenberg所做的经典工作以后[1]，带有临界的椭圆方程被众多学者所研究[2-4].当s=0时，文献[2]研究了带有临界指数的椭圆方程非平凡解的存在性和多解性，但没有给出解的性质；文献[3]利用变分方法研究一类带有奇异的临界椭圆问题的无穷多解的存在性；文献[4]研究带有p-Laplacian算子方程多解的存在性.随着对临界问题研究的不断深入，文献[5]利用一种新的对称山路引理获得了无穷多解的存在性，并给出了这些解的性质.但是对于问题(1)的研究还没有此类结果，为此本文将利用文献[5]所建立的对称山路引理获得问题(1)无穷多个解的存在性，并给出解的性质.

问题(1)对应的变分泛函为

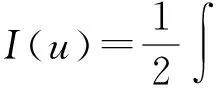
(2)

定理1 假设f(x,u)满足下列条件：

(H1)f(x,u)∈C(Ω×R,R),f(x,-u)=-f(x,u)，对任意的u∈R；

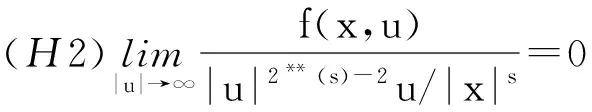
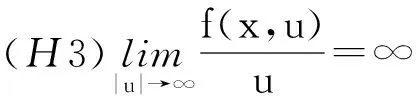
则问题(1)有一列非平凡解{un}且un→0，n→∞.

注2 如果在定理1中没有对称性条件，可利用本文中的方法得到至少一个非平凡解的存在性.本文的主要难点在于两个方面：第一个是嵌入失去紧性条件所带来的困难，我们将利用集中紧性原理[7]来克服这个困难；第二，本文中的非线性项是强不定的，致使对称的山路引理不能直接应用上去，为此我们将利用截断的方法来克服这个困难.

注3 由条件(H1)和(H2)可知

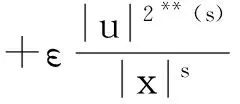
(3)

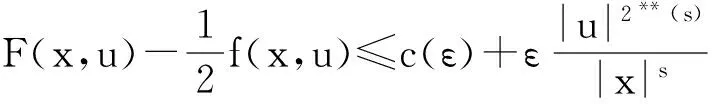
(4)

为了证明定理，首先给出如下的紧性定理，该定理的证明可以利用集中紧性原理[7]证明.

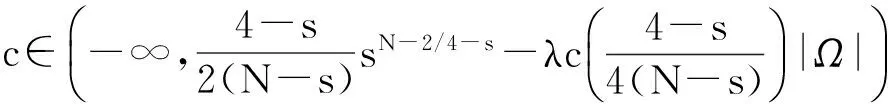
设X是一个Banach空间，记∑={A⊂X{0}：A是闭的并且关于原点戏称}.若A∈∑，定义亏格γ(A)为γ(A)=inf{m∈N,∃φ∈C(A,Rm{0})，-φ(x)=φ(-x)}.如果对任意的m∈N不存在如上定义的φ，那么约定γ(A)=+∞.令∑k为X中所有的闭对称子集A的全体，使得0∉A并且∑k≥0.

下面对称的山路引理来自于Kajikiya[5].

引理5 设E是一个无限维空间，I∈C1(E，R).如果下面的条件成立：

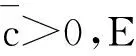
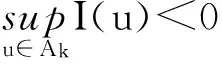
则有下面的(R1)或(R2)成立：

(R1)存在序列{uk}，使得I′(uk)=0，I(uk)<0，并且{uk}趋近于零.

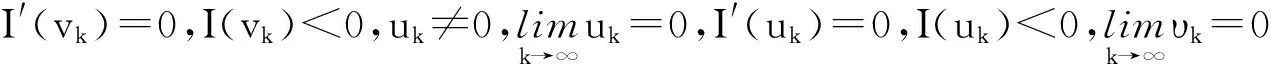
为了得到无穷多个解的存在性，需要下面的一些引理.在定理1的假设下，利用Sobolev不等式可得I(u)≥A‖u‖2-B‖u‖2**(s)-λC，其中A，B，C是某些正的常数.

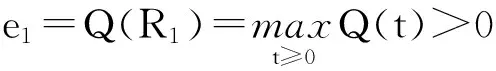
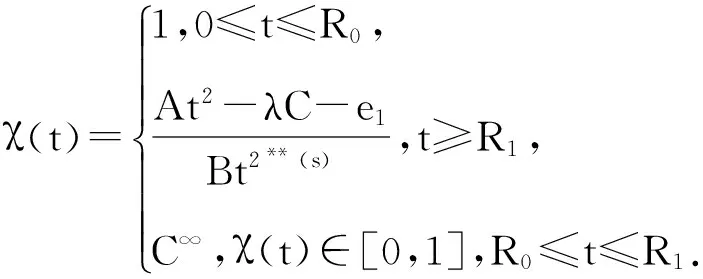
则令φ(u)=χ(‖u‖)，并考虑泛函I(u)的扰动为

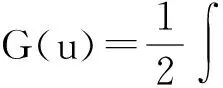
(5)

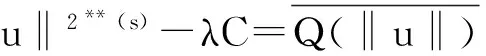
引理6 设G(u)由式(5)所给.则

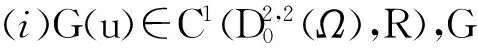
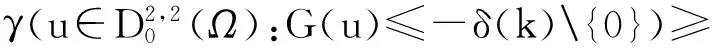
定理1的证明：

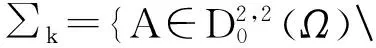
[1]H.Brezis,L.Nirenberg.Positive solutions of nonlinear elliptic equations involving critical exponents[J]. Commun.Pure Appl.Math.，1983(34):437-477.

[2]J.G.Azorero,I.P.Alonso.Multiplicity of solutions for elliptic problems with critical exponent or with a nonsymmetric term[J].Trans.Am.Math.Soc.，1991(323):877-895.

[3]X.M.He,W.M.Zou.Infinitely many arbitrarily small solutions for sigular elliptic problems with critical Sobolev-Hardy exponents[J].Proc.Edinburgh Math.Society,2009(52):97-108.

[4]N.Ghoussoub,C.Yuan.Multiple solutions for quasi-linear PDEs involving the critical Sobolev and Hardy exponents[J].Trans.Am.Math.Soc.,2000(352):5703-5743.

[5]R.Kajikiya.A critical-point theorem related to the symmetric mountain-pass lemma and its applications to elliptic equations[J].J.Funct.Analysis,2005(225):352-370.

[6]P.H.Rabinowitz.Minimax methods in critical-point theory with applications to differential equations,CBME Regional Conference Series in Mathematics[M].American Mathematical Society, Providence,RI,1986.

[7]P.L.Lions.The concentration-compactness principle in the caculus of variation:the limit case[J].I,Rev.Mat. Ibero.,1985(1):45-120.

Existence of Infinitely Many Solutions for Biharmonic Equation with Singular Potential

DAI Chen

(Suzhou Higher Infant Normal School, Suzhou Jiangsu 215008, China)

In this paper, by using variational method and concentration-compactness principle, infinitely many solutions are obtained for a class of biharmonic equation with singular potential.

biharmonic equation; concentration-compactness principle; variational method

2014-08-20

戴 琛(1980- )，女，江苏苏州人，苏州高等幼儿师范学校讲师，从事应用数学研究。

O175

A

2095-7602(2014)06-0001-03