锚节点稀疏环境下蒙特--卡罗盒定位算法*

刘 宏， 张子扬， 魏浩鹏

(江西理工大学 电气工程与自动化学院，江西 赣州 341000)

锚节点稀疏环境下蒙特
--卡罗盒定位算法*

刘 宏， 张子扬， 魏浩鹏

(江西理工大学 电气工程与自动化学院，江西 赣州 341000)

提出一种适用于锚节点稀疏环境下的蒙特—卡罗盒定位(SDANMCB)算法。算法在定位过程中将定位精度高的节点转换为虚拟锚节点来辅助其他待定位节点进行定位；同时根据采样箱的面积和附近锚节点数量调整定位所需要的样本数；滤波后根据样本的后验分布调整样本权重。仿真结果表明：算法在定位精度、采样效率上都有明显提升,并且在锚节点密度较低时定位效果有较大改善。

无线传感器网络； 锚节点； 蒙特—卡罗； 采样优化

0 引 言

在无线传感器网络(WSNs)的实际应用中，节点经常处于移动的状态，网络内节点之间约束关系不断地发生变化,如何在移动WSNs中实现节点高效、高精度定位是WSNs的研究热点之一[1]。

对于节点的移动性研究,Hu L等人将移动机器人定位中广泛应用的蒙特—卡罗定位 (Monte-Carlo localization，MCL)改进成适用于WSNs的定位方法[2]，但当锚节点密度较低时，算法的采样效率会大幅下降；之后有学者提出的蒙特—卡罗盒 (Monte-Carlo boxed，MCB)算法[3]在采样时期引入锚节点信息来锁定采样区域，以期提升采样的效率；文献[4]引入运动轨迹模型来优化采样区，对样本的权值进行优化，通过曲线拟合优化节点的采集区域，减少了采样次数，使得定位准确性有所提升。但是算法需要节点前3个时刻位置数据，导致内存空间扩大；文献[5]根据节点测距信息的误差会使节点的通信半径很难一致这一问题，通过将DV-Hop和MCL结合多跳方式来解决这一问题。但由于网络中节点时刻移动着，因此,多跳会降低定位精度；文献[6]考虑到待定位节点周围的锚节点数量并不相同，而这种差异性最终会导致节点的定位精度不同，针对这一现象提出一种基于临时锚节点的蒙特—卡罗定位方法,通过虚拟锚节点来辅助待定位节点进行定位。相较于MCB算法，该算法对节点的定位精度有所提升。

针对上述问题，本文提出一种适用于锚节点稀疏环境下的蒙特—卡罗盒(SDANMCB)定位算法，在定位中通过阈值选出定位精度好的节点来辅助其他节点定位，实现节点间的相互优化。根据采样箱面积和锚节点数量调整定位所需样本数；在粒子滤波阶段后，根据样本后验分布调整样本权重，进一步提升节点定位精度。

1 SDANMCB定位算法介绍

SDANMCB定位算法基本思想是：在采样阶段，同样考虑到不可能所有节点周围分布着一定数量的锚节点，可以将已定位二跳内邻居节点设置为虚拟锚节点来辅助定位，间接提升网络内锚节点密度；同时引进扩张系数，通过适当放大虚拟锚节点的通信距离，减小虚拟锚节点自身定位误差带来的影响。通过采样面积的大小调整所需样本数；通过离子滤波条件过滤无效样本。最后在位置估计时根据样本值与虚拟锚节点之间的距离来设置相应的权值，通过计算出待定位节点的参考位置。具体如下：

首先选择定位精度较高的移动节点为虚拟锚节点：网络内待定位节点根据2跳范围内的锚节点数量i、锚盒子面积Aachorbox来判断是否满足成为虚拟锚节点的条件，阈值可根据式(1)计算确定

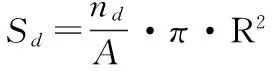
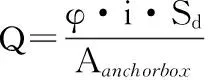
(1)

式中 nd为全网络内锚节点数量，R为节点通信半径，A为整个检测区域面积，Sd为锚节点密度，φ为样本优化因子。若待定位节点计算的Q值小于阈值1时，暂不定位，当待定位节点的Q值大于阈值1时，采用MCB算法进行定位，并将其设定为虚拟锚节点。当全网络内满足Q值的节点完成定位后，其余未达到Q值的待定位节点再进行定位。由于已定位的节点做为虚拟锚节点存在定位误差，因此,需将虚拟锚节点的通信距离适度扩张，引入扩张系数q，使其坐标更接近节点真实位置。q值根据式(2)确定

q=αAanchorbox/iR2,

(2)

式中 α为样本校正因子，优化q值的选取。选定虚拟锚节点后，再对其他节点定位。

1.1 采样阶段

待定位节点根据收到的锚节点和虚拟锚节点信息通过式(3)确定其锚盒子

i=1,2,…,n,

(3)

式中 xi,yi为节点收到的虚拟锚节点和锚节点Si的坐标，当Si为1跳锚节点时，g=1，h=0；Si为一跳虚拟锚节点时，g=1，h=1；当Si是2跳锚节点时，g=2，h=0；Si为二跳虚拟锚节点时，g=2，h=1。将锚盒子结合节点在lt时刻的位置根据式(4)构建采样盒

(4)

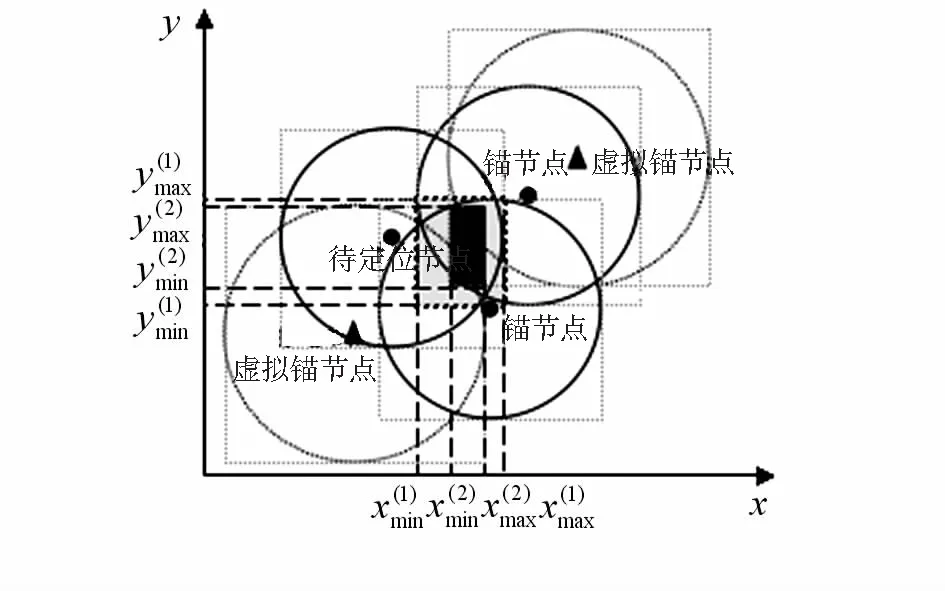
图1 SDANMCB定位算法采样区域Fig 1 Sampling area of SDANMCB localization algorithm

在MCL和MCB以及其他改进算法中，均是采集固定的样本数N个，但多数情况下，由于节点通信范围内锚节点数目不同其采样区域也不同。当节点周围锚节点数量较多，其采样区域减小，在这种情形下，可采集少量样本数即可得出精确的定位值，而不必因为N值未到，重复采样，浪费节点耗能。在此，可根据式(5)确定采样数

(5)

1.2 滤波阶段

根据粒子滤波条件去除无效的样本点。如式(6)所示

filter(lA)=(∀s1∈S1,d(lA,s1)≤R)∩

(∀c1∈C1,d(lA,c1)≤R+q)∩

(∀s2∈S2,R

(∀c2∈C2,R+q

(6)

式中 S1,S2为节点的1跳和2跳锚节点集合，C1，C2为代表节点的1跳和2跳虚拟锚节点集合，d(lA,s1)为样本lA与1跳锚节点s1之间的距离，d(lA,c1)为样本点lA与1跳虚拟锚节点c1之间的距离,d(lA,s2)表示样本点lA与2跳锚节点s2之间的距离，d(lA,c2)表示样本点lA与2跳虚拟锚节点c2之间的距离。

滤波阶段后若达不到所需采样数Nf，则重复采样和滤波步骤，直至达到采样数。

1.3 位置估计

获得满足定位要求的样本数后，对节点lA的位置进行计算。在本算法中，由于适当增加了虚拟锚节点的通信距离，因此，在位置估计时可将待定位节点根据与虚拟锚节点的距离赋予不同的权值，如图2所示：l1,l2为待定位节点，c为C1集合内的虚拟锚节点，由图可知l1在c的通信半径R内，而l2在c的通信半径R与R+q之间，l1相较l2更符合真实后验分布，由此l1所占样本权重比例高于l2。以此推理，当c为C2集合内的虚拟锚节点时，后验分布区间变换为2R与2R+q之间。

图2 样本与虚拟信标节点距离示意图Fig 2 Diagram of distance between sample and virtual beacon nodes

(7)

通过各参考值及其对应权重，便可计算出待定位节点 的参考位置。

2 仿真实验与分析

选用MCL-simulater[2]作为仿真工具，节点随机分布在500m×500m区域内, 区域内不包含任何障碍物，节点总数320个,锚节点数量32个， 节点传输模型为理想的圆，DOI=0，其通信半径R均为50m,校正因子(φ，α，ε)=(1,1,1)，采样数N=50，节点在运动速率[0,vmax]内按照随机路点运动模型(randomwaypointmodel，RWP)[7]运动，vmas=50m/s定位周期为1s。对MCL,MCB,SDANMCB定位算法进行20次仿真求平均值。

由图3看出，在整个时间段内，SDANMCB定位算法相较于MCL，MCB算法锚节点密度定位精度提升了23 %以上。由图4可看出,当Sd小于1时，本算法定位精度大大超过MCL和MCB算法，随着锚节点密度提高，算法定位误差减小，本算法由于虚拟锚节点数量的增加，其定位误差仍比MCL和MCB算法误差小。图5表明:当节点运动速度很慢时，本文算法定位精度比MCL和MCB算法有较明显的提高，随着节点运动速度的增大，定位误差增加，但本文算法定位误差仍比MCB，MCL算法低。图6中MCL，MCB，SDANMCB三种算法40s内平均采样次数分别为260,204,122，SDANMCB算法采样次数相较于MCL,MCB算法大幅降低。

图3 定位精度随时间变化图Fig 3 Diagram of change of localization precision with time

图4 定位精度随锚节点密度变化图Fig 4 Diagram of change of localization precision with anchor node density

图5 定位精度随节点运动速度变化图Fig 5 Diagram of change of localization precision with node moving speed

3 结 论

本文提出了一种适用于SDANMCB定位算法。仿真结果表明:SDANMCB定位算法与MCL，MCB算法相比，定位精度明显提升，采样次数有效降低，同时在锚节点密度较低时定位效果有较大改善，满足WSNs低功耗运行的要求。

图6 采样次数随时间变化图Fig 6 Diagram of change of sampling frequency with time

[1] Erol-Kantarci M, Mouftah H T, Oktug S.A survey of architectures and localization techniques for underwater acoustic sensor networks[J].Communications Surveys & Tutorials, IEEE, 2011, 13(3):487-502.

[2] Hu L, Evans D.Localization for mobile sensor networks[C]∥Proceedings of the 10th annual International Conference on Mobile Computing and Networking,ACM, 2004: 45-57.

[3] Baggio A,Langendoen K.Monte-Carlo localization for mobile wire-

less sensor networks[J].Ad Hoc Networks,2008,6(5):718-733.

[4] 孙 燕, 尚军亮, 刘三阳.基于采样优化的蒙特—卡罗移动节点定位算法[J].系统工程与电子技术, 2010,32(9):2001-2004.

[5] Yi J, Yang S, Cha H.Multi-hop-based Monte-Carlo localization for mobile sensor networks[C]∥2007 4th Annual IEEE Communications Society Conference on Sensor, Mesh and Ad Hoc Communications and Networks, SECON’07,IEEE, 2007:162-171.

[6] 梅 举, 陈 涤, 辛 玲.基于蒙特—卡洛方法的移动传感网节点定位优化算法[J].传感技术学报, 2013, 26(5):689-694.

[7] Harri J, Filali F, Bonnet C.Mobility models for vehicular Ad Hoc networks: A survey and taxonomy[J].Communications Surveys & Tutorials, IEEE, 2009, 11(4): 19-41.

Monte-Carlo boxed localization algorithm for sparse anchor nodes environment*

LIU Hong, ZHANG Zi-yang, WEI Hao-peng

(School of Electrical Engineering and Automation, Jiangxi University of Science and Technology,Ganzhou 341000, China)

Propose a sparse distributed anchor node Monte-Carlo boxed(SDANMCB) localization algorithm,which transfer node with high positioning precision to virtual anchor node to assist other nodes for localization;according to area of sampling box and neighbour anchor node amounts to adjust sample numbers needed for positioning;after filtering,adjust weight of samples according to posterior distribution of sample.Simulation results show this algorithm has obvious improvement in localization precision, sampling efficiency,and in low anchor node density,localization effect has great improvement.

wireless sensor networks(WSNs);anchor node;Monte-Carlo;sampling optimization

10.13873/J.1000—9787(2014)08—0131—03

2014—05—28

国家自然科学基金资助项目(61163063)

TP 393

A

1000—9787(2014)08—0131—03

刘 宏(1968-),男，江西萍乡人,教授，硕士生导师,主要研究方向为无线传感器网络。