一种快速逼近方法在施工测量中的应用研究
陈 涛,蒋茂利
(中国水电顾问集团中南勘测设计研究院有限公司,湖南长沙 410014)
一种快速逼近方法在施工测量中的应用研究
陈 涛∗,蒋茂利
(中国水电顾问集团中南勘测设计研究院有限公司,湖南长沙 410014)
基于对以复杂参考曲线为基础的建(构)筑物的施工测量计算方法的通用性和提高计算精度的目的,通过分别对常规方程和参数方程适用性的理论推导、结合工程实践并编制通用计算器程序,基本得到了所有的以复杂参考曲线为基础的建(构)筑物的施工测量计算的通用方法和计算程序。
快速逼近;施工测量;曲线平行线;计算原理;缓和曲线
1 问题的提出
施工测量的任务是将图纸上设计的建(构)筑物的平面位置和高程,按设计要求、以一定的精度在实地标定出来,作为施工的依据。很多工程上设计时使用了很复杂的曲线,在施工过程中,需要现场准确、快速地测量放样出设计曲线和(或)设计曲线的平行线(距离保持不变的两条曲线)以及该点沿设计曲线至曲线起点的长度,这给现场施工测量放样计算工作带来相当大的难度,因此研究一种通用性强、计算速度快、计算精度高的计算方法非常重要而且必要,不但可以提高工作效益,并且减少重复研究曲线的浪费和产生错误的可能。
2 计算原理及程序模板
2.1 普通方程
(1)垂距及垂足坐标计算
对于以参考曲线为基准的建(构)筑物以归化法进行施工测量放样时,必须先计算出测量点至参考曲线的垂距,再在垂直于参考曲线的断面上进行相关的计算就可以将需要的点放样到实地;测量点至参考曲线的垂足到该参考曲线初始起点的长度根据工程情况来确定是否需要计算。目前,大家一般是根据参考曲线的几何特征进行垂距计算,但当参考曲线方程很复杂,其几何特征不明显,也不能直接用公式表示的,就无法完成施工测量放样的严密计算工作。
如图1所示,设计曲线方程为y=f(x),曲线起点A0(X0,Y0),在欲放样点的附近任意测定一点A(X, Y),由坐标反算有曲线初始起点A0至测量点A的方位角α和距离S0,即:


图1 普通方程计算原理图
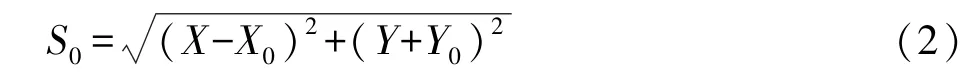
对于式(1)在使用时需要判断象限。
先对曲线求导后,曲线在起点A0处的切线方位角为:
α0=tan-1[f′(X0)]
则测量点到曲线初始起点切线的垂距(符号为左负、右正)为:
V0=S0sin(α-α0)
测量点与初始起点连线至切线的投影(符号有正、负)为:

判断T0的绝对值是否大于一个给定的值(一般取0.001 m),如果满足要求就将初始起点更换为点1#(X1,Y1),新起点坐标可按下式计算:

式(4)中T0最好取A0和切线的垂线与曲线的交点间的X差值,但为了避免复杂的方程解算(有的甚至无法用公式表达),可以根据实际曲线的情况取值,通常按式(3)中计算T0比较适合,只是循环会增加1次~2次。
更换起点后重复以上步骤(一般循环1次~5次的T0绝对值能达到0.001 m范围内),其流程如图2所示,直至不满足要求时就可得到垂足的坐标点n#(Xn,Yn),则测量点至曲线的垂距为Vn,也可以根据式(2)计算点A与垂足点n#间的距离,但要注意正、负号和方向。
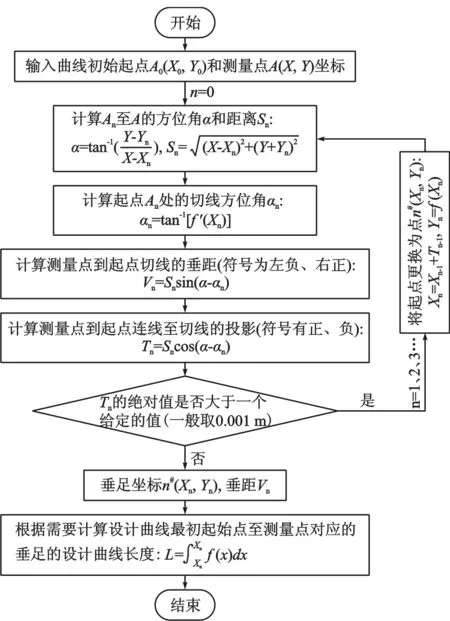
图2 垂足及垂距计算流程图
(2)曲线长度(桩号)计算
通常需要计算的曲线长度是设计曲线最初起始点至测量点对应的垂足的设计曲线长度。对于普通的曲线方程,采用对坐标的曲线积分的计算法计算,即:
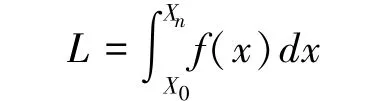
(3)程序模板
目前,在现场施工放样时主要采用的计算工具是Casio计算器,在此以Casio-fx4800计算器为编程平台,测量点至曲线的垂距及垂足坐标计算程序模板如下:
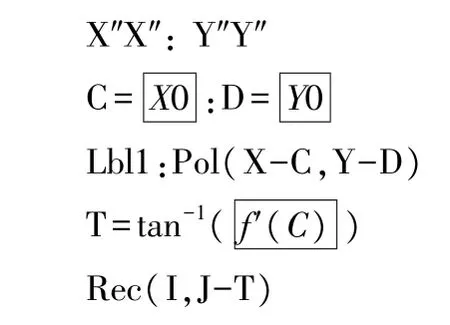

上述程序中加框加黑的函数(f(C)、f′(C))、变量(X0、Y0)和常量(0.001)分别根据设计曲线函数、选用的坐标系和放样精度的需要来确定;最后一行为显示测量点至曲线的垂距J和垂足坐标(C,D)。
2.2 参数方程
(1)垂距及垂足坐标计算
此处的参数方程是指不能用普通方程形式表示的参数方程,在此以常用的缓和曲线为例介绍参数方程的计算原理,由文献[2]有缓和曲线的方程为:

式(5)、式(6)中:(X,Y)为缓和曲线上一点的坐标,该点至缓和曲线起点(ZH点)长度为l;l0为完全缓和曲线长度;R为缓和曲线直缓点处的曲率半径。
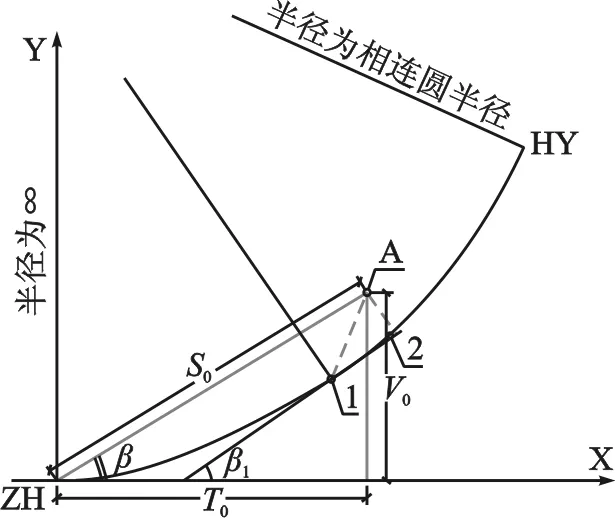
图3 缓和曲线计算原理图
如图3所示,建立以直缓点ZH为原点,过ZH的缓和曲线切线为X轴、ZH点上缓和曲线的半径为Y轴的直角坐标系,则曲线初始起点A0(X0,Y0)=(0, 0),初始起点切角β0=0。
在欲放样点的附近任意测定一点A(X,Y),由坐标反算有:
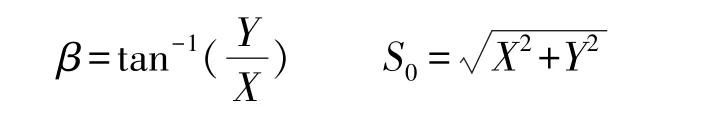
测量点到曲线起点切线的垂距(符号为左负、右正)为:V0=S0sin(β)
测量点与起始点连线至切线的投影(符号有正、负)为:T0=S0cos(β)
判断T0的绝对值是否大于一个给定的值(一般取0.001 m)如果满足要求就将起点更换为点1#(X1, Y1),新起点坐标由式(5)、式(6)有:
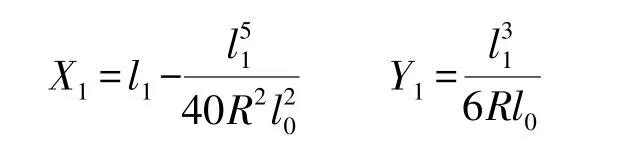
l1为缓和曲线上点1#至缓和曲线起点的曲线长,取T0。
缓和曲线上点1#的切角由文献[2]有:

更换起始点后重复以上步骤(一般循环1次~5次T0的绝对值能达到0.001 m范围内),与2.1基本相似,在此不在叙述,直至不满足要求时就可得到垂足的坐标点n#(Xn,Yn),则测量点至曲线的垂距为Vn、曲线长度ln。
(2)曲线长度(桩号)计算
对于缓和曲线的曲线长度计算,就是上述的ln,而对于其他参数方程根据其具体特性确定,在此无法穷举。
(3)程序模板
同样以Casio-fx4800计算器为编程平台,测量点至缓和曲线的垂距及垂足坐标计算程序模板如下:
X″X″:Y″Y″

以上方法既能适用于圆曲线配置对称缓和曲线的计算,也适用于配置不对称缓和曲线及卵形线的计算。对于不完整的缓和曲线(即连接两个半径不等的圆曲线的缓和曲线),在建立坐标系时要恢复成完整的缓和曲线(即连接直线和圆曲线的缓和曲线)按以上的方法建立坐标系,初始起点取不完整的缓和曲线的起点在刚建立的坐标系中的坐标。
3 结 语
本文讨论的这种快速逼近方法在满足曲线连续、在计算范围内连续可导等条件时,适用范围极其广泛。就线形而言,基本适用于所有线形,如直线、圆曲线、椭圆曲线、抛物线、指数方程曲线、对数方程曲线、缓和曲线等;就工程建筑物而言,基本适用于所有以线形为基础的建筑物,如公路、铁路、重力坝、双曲拱坝、泄洪孔洞的过流面等。
对复杂曲线施工测量放样进行了总结和研究基础上,通过实际工程的实践,这种快速逼近方法在设计曲线满足一定条件时,简化了每次遇到复杂曲线需要重新研究算法的过程,尤其适合能进行简单编程的计算工具编制一个程序能解决所有满足一定条件的所有曲线的施工测量放样的计算。所以基本上所有的施工测量放样计算程序核心只需要一个程序,之后的所有计算均在对应的断面上(包括水平断面和竖直断面)计算即可,这就使得对于施工测量放样计算通用程序的编制只需要完成相关参数的编制便可实现。
[1] 宁津生,陈俊勇,李德仁等.测绘学概论(第二版)[M].武汉:武汉大学出版社,2004.
[2] 李青岳,陈永奇.工程测量学(第二版)[M].北京:测绘出版社,1995.
[3] 同济大学数学教研室.高等数学(第三版)[M].北京:高等教育出版社,1994.
[4] DL/T 5173-2012.水电水利工程施工测量规范[S].
[5] 朱方生,李大美,李素贞.计算方法[M].武汉:武汉大学出版社,2003.
Application of a Fast Approximation Method in Construction Survey
Chen Tao,Jiang Maoli
(China’s Hydropower Consulting Group Zhongnan Survey Design and Research Institute Co.,Ltd,Changsha 410014,China)
Based on the complex reference curve based built(structure)method to calculate the construction survey of building universal and to improve the accuracy of calculation purposes,and compiled by theoretical derivation,the normal equation and parametric equation in combination with the engineering practice of general applicability of the calculator program,get all the complex reference curve the basis of building(structure)the construction survey of building a general calculation method and program.
rapid approximation;construction survey;the parallel to the curve;calculation principle;transition curve
2014—03—27
陈涛(1976—),男,高级工程师,主要从事施工测量、安全监测及管理。

