探究时间常量的公式与含义

郑 金

(凌源市职教中心 辽宁 朝阳 122500)

时间常量是高等学校教材如电子线路、电工基础和电磁学中与暂态电路密切相关的一个比较重要的物理量.暂态电路的充电或放电过程属于瞬态过程，而时间常量是瞬态过程的一个特征量，不同的瞬态过程具有不同的时间常量公式.下面按3种情况举例分析.

1 在线性力作用下的物体做变速直线运动过程的时间常量

包括两种情形，一是物体受恒定动力和线性阻力共同作用的变加速直线运动过程；二是物体只受线性阻力作用的变减速直线运动过程，都为瞬态过程.而线性力是指与速度成正比的力f=kv.

【例1】如图1所示，光滑U型金属导轨PQMN水平固定在竖直向下的匀强磁场中，磁感应强度为B，导轨的宽度为l，QM之间接有阻值为R的电阻，其余部分电阻不计.一质量为m，电阻也为R的金属棒ab放在导轨上，给棒一个水平向右的初速度v0使之开始滑行，最后停在导轨上.由以上条件，在此过程中可求出的物理量有[1]

图1

A.在电阻R上产生的焦耳热

B.通过电阻R的总电荷量

C.ab棒的运动位移

D.ab棒的运动时间

解析[2]：由能量守恒定律可知焦耳热为

金属棒所受合外力为安培力

F=Bli

电流随时间而变化，则安培力对时间的平均值为

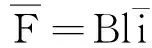
由动量定理有

可得总电荷量为

电路中的电流为

金属棒受到的安培力为

令

则安培力的冲量为

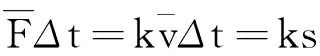
因此由动量定理有

-ks=0-mv0

所以位移为

故答案为选项A，B，C.

那么“选项D”为什么不可求？下面进行分析.

由牛顿第二定律列微分方程为

可变形为常系数线性微分方程的标准形式

稳态速度为v=0，利用瞬态过程的结论[3]可得速度与时间的关系式为

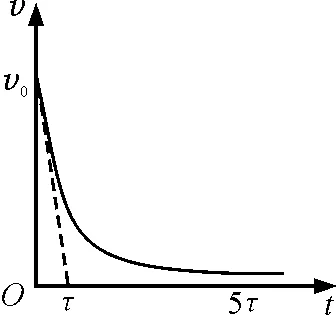
图2

利用积分公式

可知图像与坐标轴在区间[0,t]上围成图形的面积为

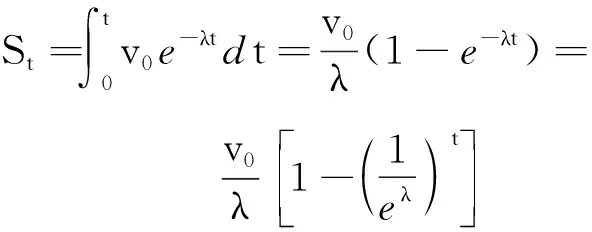
(1)

因此在全区间的最大面积为

这表明，按指数规律递减的速度图像的面积即位移等于速度初始值与时间常量之积.

在数学上，运动时间趋于无穷大，但运动位移却为有限值.这与无穷递减等比数列的和相似，如

虽然项数无限，但其和为定值1[2].

对于

由等比数列前n项和公式可知

(2)

可见式(1)、(2)相似，都为递减指数函数，因此只有当自变量无限大时，和才为有限值.由于关系式中的时间变量在数学上为无穷大，所以不可求.

2 暂态电路充电和放电过程的时间常量

2.1 RL暂态电路

【例2】如图3所示为RL串联电路，电阻R与纯电感线圈串联，线圈的自感系数为L，直流电源内电阻不计，那么当闭合开关的瞬时，电路中的电流将如何变化呢[4]？

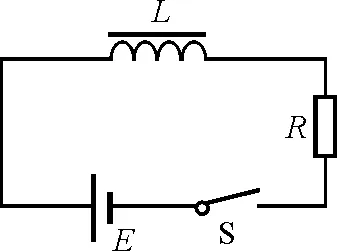
图3

解析：当开关S闭合后，由于电路中的电流从无到有，突然增大，则线圈产生自感电动势为

它将阻碍线圈中电流的增大，使电流不能立刻达到最大值，而是经历一定的时间才能达到最大值，所以电流的变化过程是瞬态过程.由基尔霍夫电压定律列出回路电压方程为

E-UR-UL=0

即

变为标准形式

i=i+(i

对函数关系式取导数并将t=0代入，可得过图像起点切线的斜率为

表明图像的切线与渐近线交点的横坐标为τ，等于时间常量.

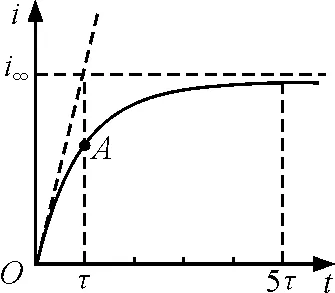
图4

对于指数函数

x=x+(x0-x

若x=0，则有

如高中的断电自感实验，在断开电源之后，通过线圈的感应电流变化规律为

其中

可见，放电电流随着时间变化的关系为单调递减，其图像与图2相似.从数学角度来看，断电后感应电流持续的时间无限长；而在实际上，经过时间5τ时，感应电流i=0.006 7i0，一般就可以认为电流已减弱为零了，即感应时间也是有限的，所以物理上把这一过程称之为暂态过程[1].

对于指数函数

x=x+(x0-x

若

x0-x=b>0

则

x=x

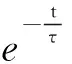
表明图像起点的切线与渐近线交点的横坐标为时间常量τ.

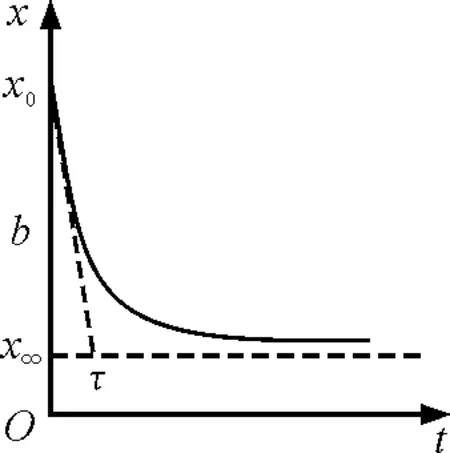
图5

所以，瞬态过程的变量随时间呈指数规律变化的图像是以x=x=f()为渐近线的指数曲线，指数曲线起点的切线与渐近线交点的横坐标为时间常量τ.若从变化率的角度而言，则初始变化率等于变化量的最大值与时间常量之比.

如图4中的A点，当t=τ时，有

则iA=0.63i.这表明，时间常量是表示瞬态过程的变量已经变化了总量(瞬态过程变化量的最大值)的63%所经历的时间[4].

由于最大变化量x，x0或b=x0-x是一定的，则时间常量τ越小，指数曲线就越陡直，变量的变化就越快；反之，时间常量τ越大，指数曲线就越平缓，变量的变化就越慢.因此时间常量是反映瞬态过程变化快慢的物理量.

以上几方面是暂态电路时间常量的含义，也是瞬态过程中时间常量的含义.

2.2 RC暂态电路

【例3】如图6所示的闪光灯电路中，电源的电动势为E，电容器的电容为C，当闪光灯两端电压达到击穿电压U时，闪光灯才有电流通过并发光，正常工作时，闪光灯周期性短暂闪光，求电容器两端的电压uC如何变化.试画出uC-t图像[5].

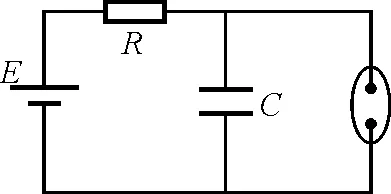
图6

解析：(1)在电容器充电过程中，闪光灯相当于开路，电容器与电阻R串联，组成RC串联电路.

已知电容器电压的初始值为u0=0，当瞬时值为uC时，电容器中增加的电荷量为q=CuC，则充电电流为

对RC串联电路由闭合电路的欧姆定律有E=iR+uC.即

这是关于uC的一阶常系数微分方程.由此可知电压稳态值为u=E，时间常量为τ=RC，而电容器电压的初始值为u0=0，利用瞬态过程的结论可知电容器两端电压随时间的变化规律为

表明在充电过程中电容器两端电压随时间按指数规律变化.

那么电压的最大值和最小值分别是多少呢？下面通过图像来说明.

闪光灯与电容器并联，其两端电压等于电容器两端电压.在RC串联电路充电过程中，当电容器两端电压升高到一定值U2时，闪光灯开始导通，相当于开关闭合，电容器开始放电，因此电压的最大值为U2.

当闪光灯导通时，电容器开始放电，相当于整个电路有两个电源，但由于导通电阻r比分压电阻R小得多，因此可近似认为电阻R起断路作用，将电源E与电容器隔离，那么电容器与闪光灯组成rC串联电路，在闪光灯中产生放电电流，即

则由闭合电路的欧姆定律有uC=ir，即

可知时间常量为τ=rC，而放电初始电压为U2，所以电容器两端电压随时间的变化规律为

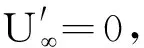
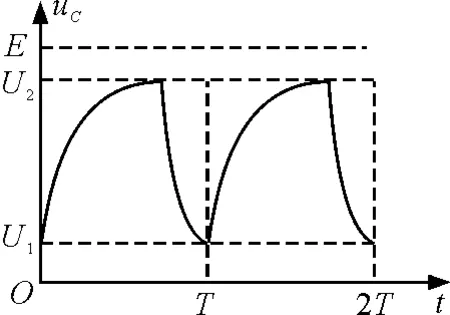
图7

3 原子核衰变过程的时间常量

【例4】放射性强度定义为放射性物质在单位时间内发生衰变的原子核的数目，由统计规律可知，当原子核数目足够大时，在衰变过程中，放射性强度跟当时存在的原子核数目成正比，其比例常数用λ表示，称为衰变常量.天然铷由稳定同位素85Rb(占72.15%)和放射性同位素87Rb(占27.85%)组成，具有放射性，已知RbCl的分子量为120.92，由阿伏伽德罗常数可推出1 g的RbCl含有87Rb的初始原子核数N0.若实验测得质量为1 g的RbCl的放射性强度是I0，试求87Rb在衰变过程中的衰变常量λ,时间常量τ,半衰期T和平均寿命t0(都用N0和I0表示)[6].

解析：设某时刻未衰变的放射性原子核总数为N，在很短时间dt内，原子核的变化量为dN，因衰变时原子核数目减少，则增量dN为负值，带上负号为正值，故原子核数变化率应为

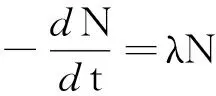
可得关于变量N的一阶常系数线性微分方程为

可知稳态值为f()=0，时间常量等于衰变常量的倒数.

设初始值为f(0)=N0，利用瞬态过程的结论可知微分方程的解为

这就是原子核剩余量N随时间t变化的关系即衰变规律的表达式，称为衰变定律[7]，图像如图8所示.

图8

放射性强度即放射性原子核数目的变化率为

即I0=λN0.已知实验测得质量为1 g的RbCl的放射性强度是I0，只有其中的87Rb具有放射性，因此87Rb的初始放射性强度是I0.而1 g的RbCl含有87Rb的初始原子核数N0，所以87Rb在衰变过程中的衰变常量为

那么时间常量为

每经过一个半衰期的时间，原子核数量衰变一半，则剩余量为

可得87Rb的半衰期为

从衰变图像可知，对于一定数量的原子核，在整个衰变过程中，有的一开始就衰变了，存在的时间为零，则其寿命为零；有的经过时间为τ时发生衰变，存在的时间为τ，则其寿命为τ；有的很久才衰变，存在的时间很长，则寿命很长；有极少数的经过无限长的时间发生衰变，则寿命为无限长.把各原子核衰变前存在时间的平均值，即放射性元素组成物质的原子核寿命的平均值，称为放射性元素的平均寿命[7].从物理量的角度而言，对一个研究对象的过程量取平均值没有意义，但这里的时间是各原子核对应的时间，因此可以取平均值，即为整个衰变过程中各原子核存在时间的平均值.

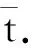
在图8中，递减指数图像与坐标轴围成图形的面积为S=N0τ，而矩形面积为S=N0t0，由二者相等可得时间的平均值为t0=τ，所以原子核的平均寿命在数值上等于衰变过程的时间常量，即

虽然衰变时间为无穷大，但图像面积却为定值，即原子核衰减图像的面积等于初始值与时间常量之积.

以上几方面是原子核衰变过程时间常量的含义.

由图2和图5可知，指数曲线与纵轴和渐近线围成图形的面积，等于变化量的最大值与时间常量之积，而且过曲线起点的切线平分该面积，这是指数瞬态过程时间常量的含义.

参考文献

1 钱爱华.运动时间是无限还是有限.物理通报，2013(1):128

2 丁广华.运动时间为什么不可求？物理教师，2012(3)：59

3 郑金.利用结论巧解“甲虫和橡胶带”问题.物理通报，2012(4):61

4 周绍敏.电工基础(第三版).北京：高等教育出版社，2005.82，133

5 何勇军.例谈含电感与电容类电路问题的解题策略.中学物理，2012(1)：59

6 罗维治.新编物理奥林匹克教程.长沙：湖南师范大学出版社，2001.530

7 曹良腾.对原子核衰变的小议.物理教学，1992(11):34