小波变换在多层复合材料的超声波检测中的应用

朱建峰，郭伟剑，刘俊邦，华鹏翔

(武汉军械士官学校，武汉430075)

小波变换在多层复合材料的超声波检测中的应用

朱建峰，郭伟剑，刘俊邦，华鹏翔

(武汉军械士官学校，武汉430075)

针对多层复合材料深层界面脱粘检测中回波信号信噪比低和难以分辨的难题，将小波变换引入到回波信号的超声波检测中来;分析了小波变换及多分辨率分析的理论依据，针对回波信号首先进行小波去噪，然后提取小波变换后各频段的信号能量作为特征，为缺陷分析及识别提供依据;实验结果表明:小波阈值去噪算法的改进方案明显要比单纯的硬阈值和软阈值方法降噪效果好，信号分析方法并可有效提取信号的特征，并将缺陷识别、定位。

多层复合材料;小波变换;超声波检测;阈值去噪;特征提取

超声波检测技术因其具有快速准确、易于控制、无损伤等特点，近几年来成为国内外应用最广、发展最快的一种无损检测技术。当检测对象为多层复合材料时(本文以固体火箭发动机为例)，由于各层材料的声阻抗严重失配，使得经深层缺陷返回的超声波回波信号非常微弱，而且各层缺陷信息叠加在一起，使得深层界面脱粘检测变得非常困难，不能用传统的滤波和模型进行处理，给缺陷识别和信号处理带来了极大的困难。

经研究采用小波变换可以从复杂的回波信号中提取缺陷信号，这是因为小波变换在超声波检测中具有以下两方面的功能:小波变换可以将回波信号中大量的噪声滤掉，从而消除噪声的影响;小波变换能有效地提取出缺陷信号及其特征。

1 小波变换及多分辨率分析

小波变换是一种时间——尺度(时间——频率)分析方法，具有多分辨率分析的特点，在时频域都具有表征信号局部特征的能力，所以被称为分析信号的显微镜。

设L2(R)指R上平方可积函数构成的函数空间，如果ψ (t)∈L2(R)，其傅里叶变换为^ψ(ω)满足容许性条件，如式(1)所示:

即Cψ有界，则称ψ为一个基小波或母小波。定义下式(2):

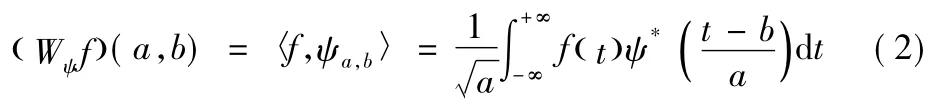
为关于基小波ψ的连续小波变换。式(2)中，ψ*(t)为小波函数ψ的共轭，f(t)为用于变换的信号，a为尺度因子(伸缩因子)，b为平移因子。

在实际问题的数值计算中常采用离散形式，即离散小波变换(DWT)。DWT可以通过离散化伸缩因子a和平移因子b来得到。通常取a=am0，b=nb0am0，m，n∈Z，相应的离散小波变换如式(3)所示:

多分辨率分析(MRA)是用小波函数的二进伸缩和平移表示函数这一思想的更加抽象、复杂的表现形式，它形成了构造正交小波基的一个框架。实际中采用Mallat算法即信号的塔式多分辨率分析分解与重构的快速算法，它是在多分辨率分析的基础上提出的。

若Sk是信号S的离散采样数据，Sk=cA0，k，则信号S的小波分解公式为式(4):

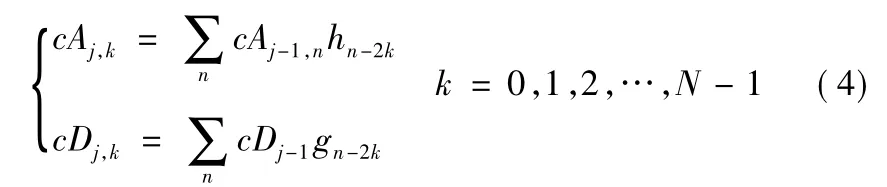
小波变换的重构过程是分解过程的逆运算，相应的重构公式为式(5):

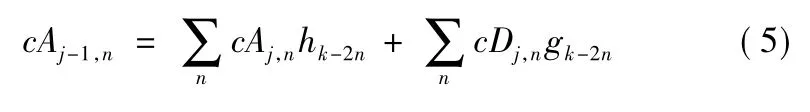
2 小波变换在超声信号去噪中的应用

采样的超声波回波信号中含有大量的噪声，若不能对信号进行有效地去噪处理，将会导致缺陷判定的困难。采用小波降噪算法能有效地降低噪声干扰，利于下一步提取有用的缺陷信号。对信号连续做几次小波分解后，原始信号所对应的各尺度上的小波系数在某些特定的点的位置有较大的值，而在其他大部分位置的值都比较小;对于白噪声信号，它在每一尺度上所对应的小波系数是均匀的，并随尺度的增加，系数的幅值有所减小。因此，经小波分解后，信号的小波系数幅值要大于噪声的信号幅值，于是可以选取一个合适的λ作为阈值，当小波系数的幅值大于阈值λ时，认为这主要是由真实信号引起的，从而保留该系数;当小波系数的幅值小于阈值λ时，认为这主要是由噪声引起的，将该系数赋零值，从而实现了信噪的分离。在信号的去噪过程中，阈值的选取和量化是非常关键的，可以说，直接影响消噪的效果。因此，在应用时，应根据具体情况决定阈值的选取方法和量化规则。

传统的硬阈值和软阈值两种处理方法虽然得到了广泛的应用，并取得了不错的效果，但它们本身都还存在一定缺陷:硬阈值处理方法由于收缩函数的不连续性，会使估计得到的信号产生附加振荡;软阈值处理方法的连续性较好，但估计得到的小波系数与实际的小波系数总是存在恒定的偏差λ，这将在一定程度上影响重构信号与真实信号的逼近程度，从而造成不可避免的误差。因此，本文采用了软、硬阈值折衷法的阈值估计方法，能有效弥补硬阈值和软阈值的不足。

软、硬阈值折衷法如式(6)所示

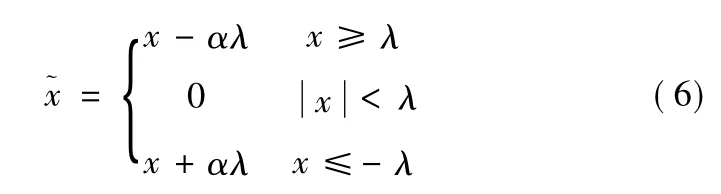
α(0≤α≤1)为调整系数，它可以提高阈值选取的灵活性，在实验时能够达到更好的滤波效果。α因子的大小决定了消噪后信号的信噪比，α越大，信号失真越多，振荡越小;α越小，信号失真越少，振荡越厉害。分解尺度的大小也对消噪后信号的信噪比有着很大的影响，分解尺度过小，不能将噪声同信号完全分离，分解尺度过大，则会造成较大的信号失真。过大、过小的α因子和分解尺度都会导致信噪比的降低，必须选取合适的α因子及分解尺度。

为了比较不同阈值降噪方法的降噪效果，采用信噪比和对均方误差作为评价标准。信噪比的公式为式(7)

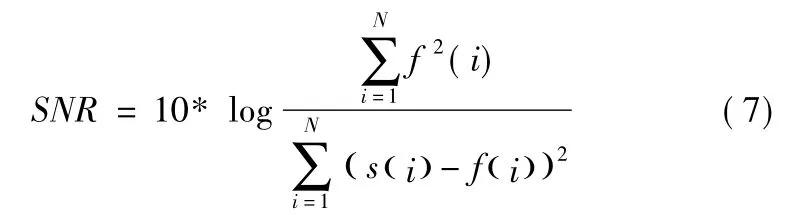
相对均方误差的公式为式(8)

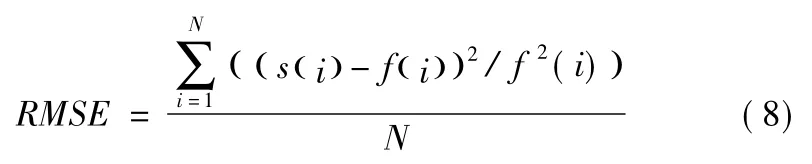
式(7)、式(8)中:f(i)为原始信号;s(i)为含噪信号;N为信号长度。

对一段超声波回波信号加随机噪声后分别利用硬阈值法、软阈值法和软、硬阈值折衷法做了降噪仿真实验，经多次实验比较后，实验最终确定选用db3小波，分解尺度为4， α因子取为0.78，阈值选择实验结果如图1所示。3种不同方法降噪前后信噪比和相对均方误差如表1所示。

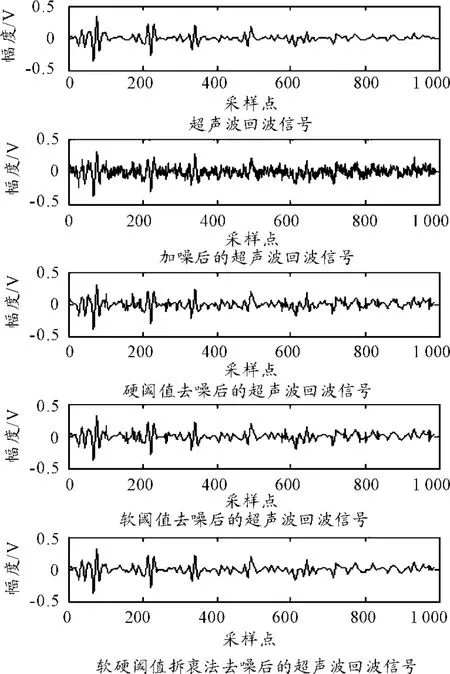
图1 3种阈值降噪实验结果

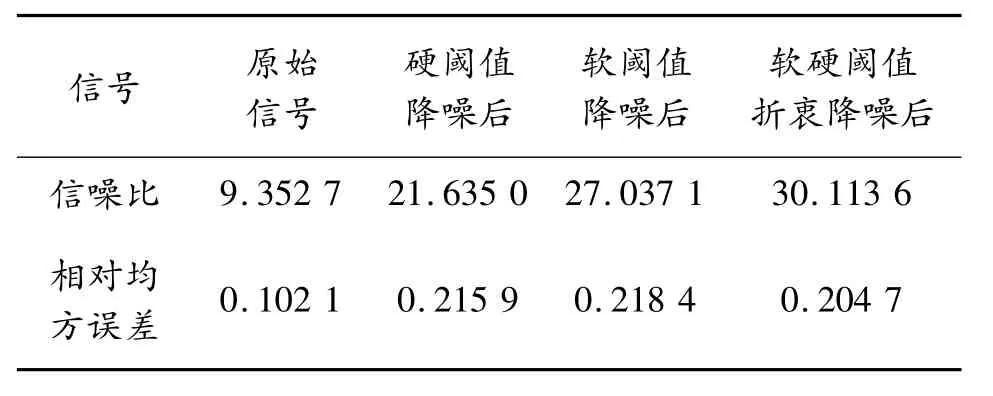
表1 3种方法去噪结果

分析图1以及表1可以发现，硬阈值方法处理后的缺陷信号失真最小，但是信号振荡比较剧烈，这在一定程度上降低了信噪比，也不利于对缺陷信号做出判断;软阈值方法处理后的信号比较光滑，振荡很小，但缺陷失真较大，这也影响了信噪比的提高，对于利用缺陷信号来判断材料缺陷的尺寸、位置、类型等信息也十分不利。而利用本文的软、硬阈值折衷法对含噪信号进行消噪处理，有效地改进了软、硬阈值去噪法的缺点，获得了更好的去噪效果和更高的信噪比增益。

3 小波变换在超声信号特征提取中的应用

由于回波信号十分微弱且混有大量干扰信号，若想确定深层界面的反射信号，必须采用信号处理的方法实现，采用小波多分辨率分析的方法提取深层界面信号。由于连续小波变换会带来较多的冗余信息，且小波函数的选取对变换的结果影响很大，所以采用离散小波变换，利用变换后各频段信号能量的差异来进行深层界面信号的分析和特征提取。

固体火箭发动机外壳材料为30铬锰硅(30CrMnSiA)合金钢，隔热涂料的主要成分为:有机硅树脂、白云母粉、三氧化二铬。纵波在钢和复合材料中的声速分别为5 900 m/s、2 200 m/s;声阻抗分别为4.66×106g·cm－2·s－1、3.63× 105g·cm－2·s－1。

超声波垂直入射时，当粘接情况良好时，相当于超声波经壳体直接进入绝热层，壳体与绝热层之间反射率如式(9):

式(9)中:Z绝为绝热层的声阻抗;Z壳为壳体材料的声阻抗。

当存在脱粘时，相当于超声波经壳体射入空气，壳体与空气之间反射率为式(10):

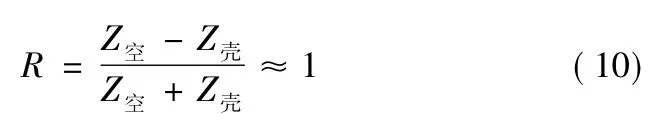
式(10)中，Z空为空气的声阻抗。

当存在脱粘的情况时，超声波反射率接近于1，透射率趋于0，几乎完全被反射。而当粘接良好时，超声波反射率约为86%，约有14%的能量进入下一层介质。超声波在其他层的传播规律也是如此。所以，可以通过超声波透射或反射的声波能量来分析各个界面的粘接情况。

对超声波回波信号f(t)进行小波分解，得到分解后的序列Sj(j=1，2，…)，则各频率段能量Ej及信号总能量E分别为式(11)、式(12)所示:

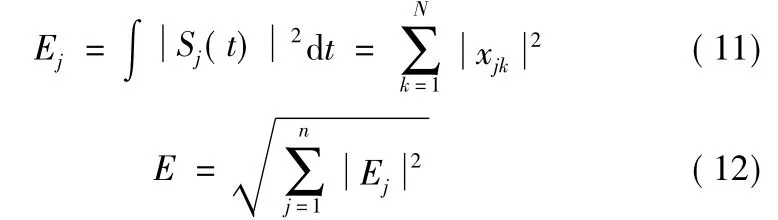
式(11)中:xjk(j=1，2，…，n;k=1，2，…，N)表示重构后信号Sj的离散点幅值;n为小波分解层数;N为重构后信号Sj的长度。

图2中所示为时域中检测的回波信号，无法判断各层的具体粘接情况，因此采用小波变换对信号进行分解，然后计算各层重构后的能量，从而提取出信号的特征，实验中选用db3小波，对信号进行6层分解。

各层的能力值如表2所示。表2中，E0代表回波信号傅里叶变换后的信号，E1～E6代表小波分解后各个频段的能量。从表2中可以看出，无脱粘信号与第一层脱粘信号较容易分辨，而无脱粘信号与第二层脱粘信号的能量则相差很小。

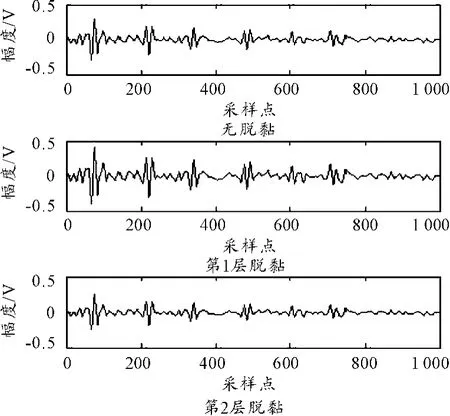
图2 3种阈值降噪实验结果

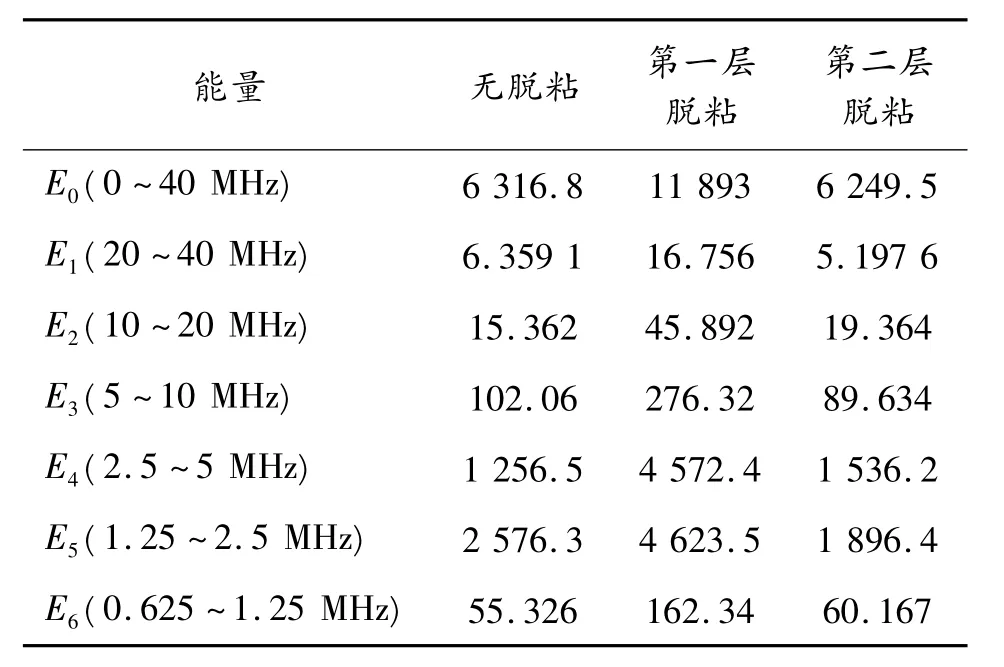
表2 3种状态下各频带的能量

由于检测仪的采样频率为80 MHz，根据采样原理，理论上采集到的信号最高频率为40 MHz。在实验中，采用的是中心频率为2.5 MHz的超声直探头，所以回波信号应主要分布在以探头中心频率为中心的频带范围之内，有用的信号能量为E4和E5。从各层能量表中可以看出，超声波回波信号也主要分布在d4、d5的频带中。这也与前面信号在各个分解频带内的分布规律一致。仔细对比E4和E5可以看出，无脱粘情况下，相当于超声波检测信号在钢层和两层复合材料中传播，由于复合材料对超声波的衰减较大，且衰减系数与频率有密切关系，频率越高，衰减越快，所以E4要比E5下降得快。第一层脱粘情况下，相当于超声波只在钢层中传播，所以E4和E5相差不大。第二层脱粘情况下，相当于超声波在钢层和第一层复合材料中传播，所以E4要比E5下降稍快，但两者差距要比无脱粘情况下小。

可以根据各频段内能量的差异对信号的特征进行提取，提取出来的特征可用来识别多层界面的脱粘缺陷，并用于定位缺陷的位置。

4 结论

根据超声波回波信号的特点，将小波变换技术引入到了超声波信号的处理中。首先介绍了小波变换的基本原理，然后论述了小波变换在超声波信号检测中的作用:信号去噪和信号特征提取，并对小波基函数、分解层数和去噪方法的选择进行了理论研究与实验验证。实验结果表明:小波变换技术可以有效地从被噪声淹没的信号中将超声波有用信号提取出来。小波分析，在超声波信号检测中具有极大的优越性。

［1］罗雄彪，陈铁群.超声无损检测的发展趋势［J］.无损检测，2004(3):21－23.

［2］NOWACKIK.Possibility of determining steel grain size using ultrasonic waves［J］.METALURGIJA，2009，48(2): 113－115.

［3］李树钰.改进的小波阈值去噪法及其在MATLAB中的仿真［J］.噪声与振动控制，2010(1):121－123.

［4］隋玉堂，杨兴根.火箭发动机界面脱粘分析及检测新方法［J］.飞航导弹，2001(1):43－46.

［5］王亚，吕新华，王海峰.一种改进的小波阈值降噪方法及Matlab实现［J］.微计算机信息，2006，22(2－3):259－261.

［6］潘明海，李雅倩，齐雪莲.一种改进的小波阈值去噪法［J］.无线电工程，2006，36(5):30－32.

(责任编辑周江川)

Application of W avelet Transform in Ultrasonic Detect in M ultilayer Com posite Materials

ZHU Jian－feng，GUOWei－jian，LIU Jun－bang，HUA Peng－xiang
(Wuhan Ordnance N.C.O Academy of PLA，Wuhan 430075，China)

Aiming at the problem of low signal－to－noise and serious overlap of the echo signals from multilayer compositematerials deep－seated interface non－felt detection，the wavelet transform method was introduced to ultrasonic detection of echo signals.Theory ofwavelet transform andmulti－resolution analysiswas analyzed，aiming at echo signals，wavelet de－noising firstly，than the energy which were extracted from detection echoes in different frequency range after wavelet transform.The results show that the improved method ofwavelet de－noising threshold is better than traditional threshold strategy in de－noising，the signals analysismethod is effective for the extraction of signal information and it also can identify and locate defects.

multilayer compositematerials;wavelet transform;ultrasonic detect;de－noising threshold;information extract

:A

1006－0707(2014)07－0067－04

format:ZHU Jian－feng，GUOWei－jian，LIU Jun－bang，et al.Application of Wavelet Transform in Ultrasonic Detect in Multilayer Composite Materials［J］.Journal of Sichuan Ordnance，2014(7):67－70.

本文引用格式:朱建峰，郭伟剑，刘俊邦，等.小波变换在多层复合材料的超声波检测中的应用［J］.四川兵工学报，2014(7):67－70.

10.11809/scbgxb2014.07.020

2013－10－10

国家自然科学基金项目(50805145)。

朱建峰(1986—)，男，硕士研究生，主要从事现代测试技术及仪器研究。

TP274.2