非惯性系下旋转压电层合悬臂梁的动力学建模及控制

张 娟， 舒亚锋， 刘自强， 白 斌， 杨未柱

(西北工业大学 力学与土木建筑学院， 陕西 西安 710129)

0 引言

旋转柔性悬臂梁的动力学建模和振动控制在航天器、机器人及高速旋转机构等工程领域具有独特的理论和应用价值.很多工程结构可以理想化为旋转悬臂梁，比如空间机械臂、空间太阳能帆板、大型空间天线等.许多学者如Yoo H H[1]、洪嘉振、刘锦阳[2]、和兴锁[3]等建立了旋转柔性悬臂梁动力学模型，在刚-柔耦合建模理论方面已比较成熟.

近20年来，随着智能材料的兴起，利用智能材料 抑制航天器上柔性部件的振动[4-7]，是解决空间机械臂末端振动问题的有效方法之一.Crawely[8]研究了梁与压电片之间的作用力，开辟了以压电陶瓷材料作为作动器的振动主动控制结构的研究，之后新的研究成果不断出现.但是以往的研究大都是片式作动器[9]，并且携带压电传感器，是一种反馈主动控制[10]方法，这种控制系统比较复杂，而且具有时滞性.而使用平铺压电层的智能梁进行振动主动控制的研究是近年来的热门话题.本文模型不需压电传感器，对做旋转运动的柔性悬臂梁[11,12]，在梁表面平铺压电层作为作动器，利用有限元法进行RPLCB模型的动力学建模，并设计一种逆动力学控制方法[13]对梁的末端振动进行振动控制.

1 旋转压电层合悬臂梁的动力学建模

(1)

下层压电层的压电方程为：

(2)

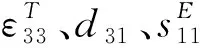
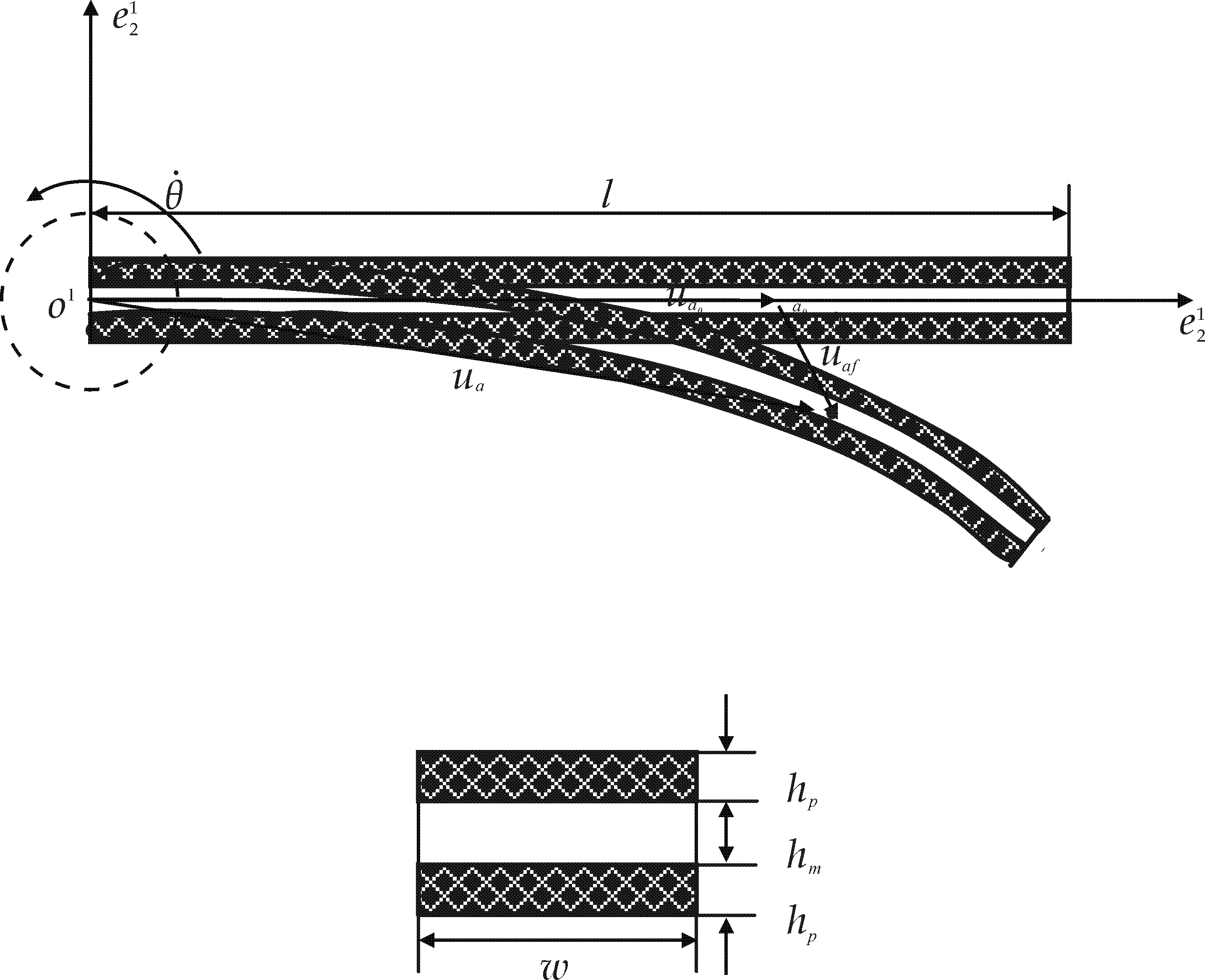
图1 RPLCB梁模型

根据Hamilton原理可得

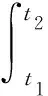
(3)

势能包括两部分：基体的弹性势能和上下两层压电片的应变能(包括弹性势能和电能)，其中Up1(t)、Up2(t)分别表示上下两层压电片的应变能.

(4)

结合(1)式，可求得e单元的应变能

(5)

其中k为梁的弯曲曲率，忽略剪切效应.

同理可求得

(6)

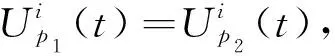
(7)

在压电层极化表面施加交变电压U(t)=hpE3时，则压电层合悬臂梁上形成变化的电场E3，由于压电效应，梁会发生弯曲变形产生弯矩Me(t)：

Me(t)=

(8)

其中，Ep为压电陶瓷的杨氏模量，

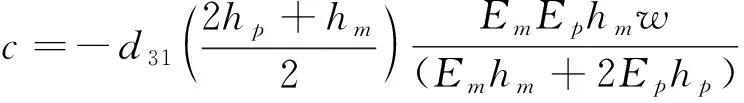
(9)

上式中ψ是形函数N1、N2对x的偏导数.则外力对应的广义力为

(10)

在惯性系下的动能矩阵表达式为

(11)

其中Ne,1、Ne,2为单元形函数,对于压电平面柔性梁，不计分布外力(包括重力)，其动力学方程为

(12)

其中，

(13)

(14)

(15)

(16)

(17)

2 算例及仿真分析

2.1 RPLCB梁端点的响应特性

本文旋转梁旋转角速度变化规律

(18)

物理参数为：弹性模量E=6.895 2×1010N/m2，密度ρ=2.766×103kg/m3，长度l=8 m，w=0.01 m,hm=0.005 m,hp=0.001 m;惯量矩IZZ=2.9×10-10m4，横截面积A=7×10-5m2，加速时间为T=15 s,取Ω1=2 rad/s，Ω2=4 rad/s.本文的压电陶瓷用PZT-5H ,基体材料选用45#钢，参数[14]如表1所示.

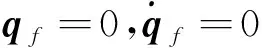
图2给出了两种稳定转速下的RPLCB梁末端浮点坐标系下的横向变形位移.从图中看出，在高转速下，计算结果有发散趋势，这是由系统非线性引起的.

从图3可知，由于梁旋转时离心力的存在，使梁始终处于伸长状态.但是与图2所示的横向位移相比，轴向变形是10-5量级，可以忽略.因此将只对梁的横向变形位移进行控制.

图4是梁端点在浮点坐标系下的横向加速度响应.在初始阶段4 s之前，加速度一直增大，在4.5 s后，逐渐处于平稳状态.

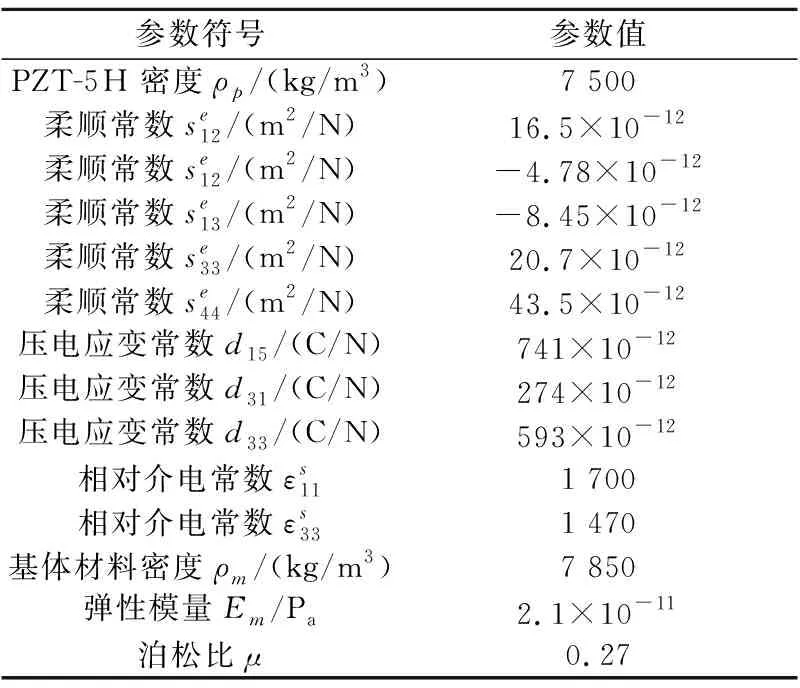
表1 PZT-5H与基体材料参数

图2 梁端点浮点坐标系下的横向变形位移方向)

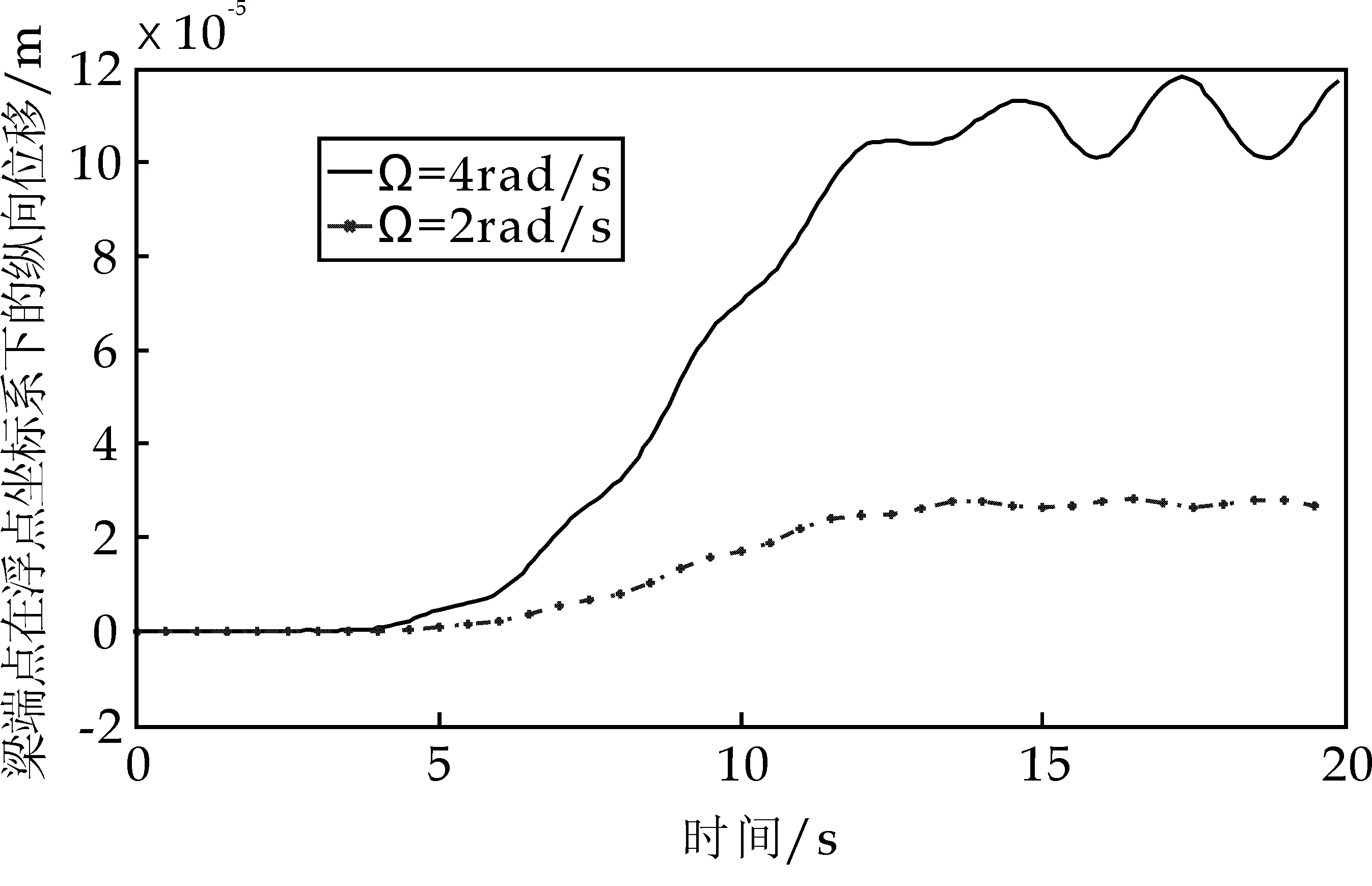
图3 梁端点浮点坐标系下的轴向变形位移方向)

图4 梁端点浮点坐标系下的加速度

2.2 控制电压计算算例

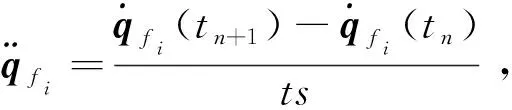
设控制律为ζ(t)，控制后的位移为Y=ζ(t)·X,本文目标是梁在浮点系下的位移最小，约束是方程的解收敛，即可求出控制电压.令ζ(t)=0.5时，

(19)

将式(13)求得的Qqfi代入式(10)中，可得弯矩Mei(t)，代入式(9)，可得控制电压U(t).

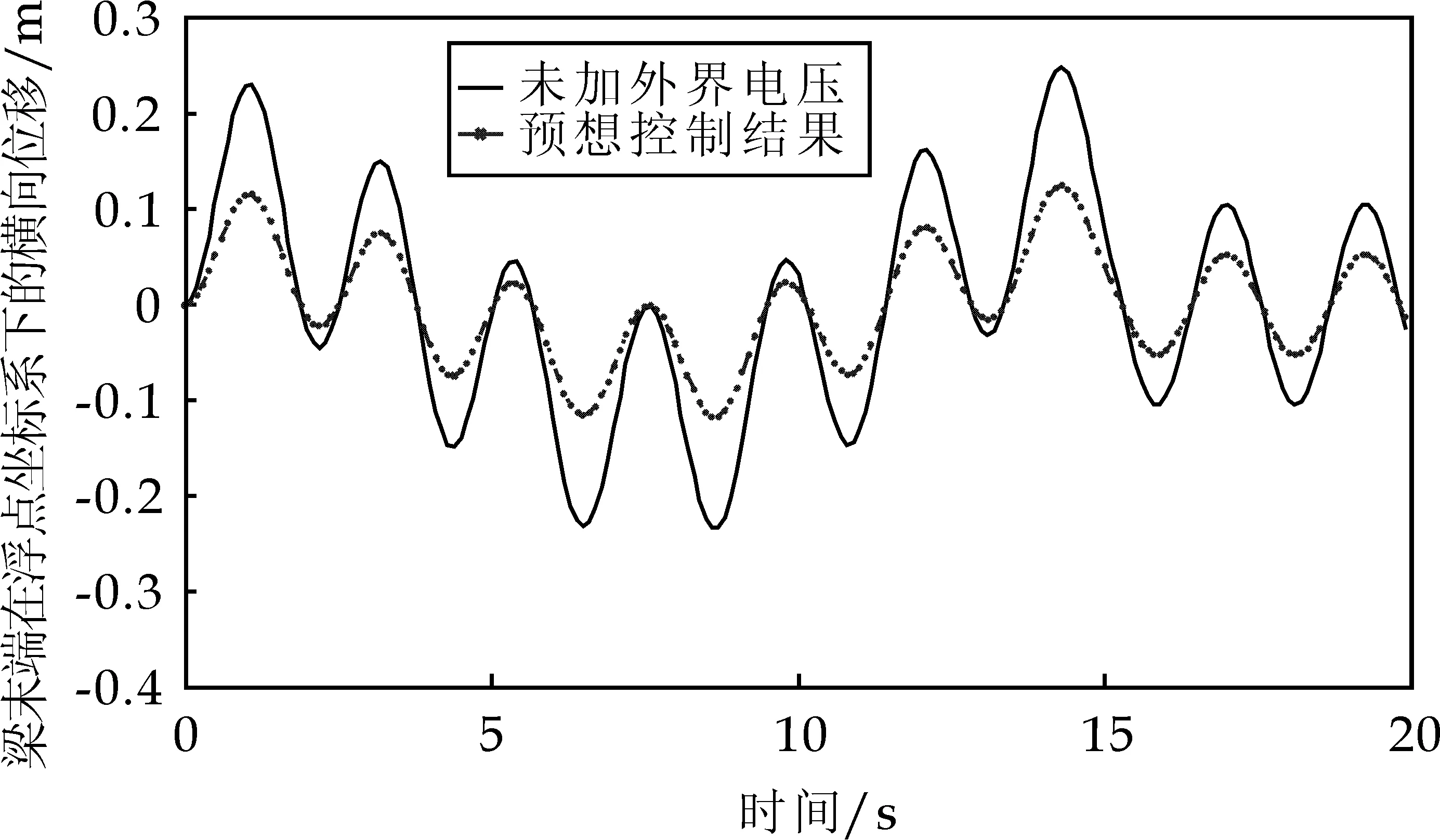
图5 梁端点横向位移的预想控制前后对比图

设预想使得末端横向位移振幅衰减为50%，根据图5所示的预想控制结果逆推出控制电压如图6所示，从图中可以看到电压随时间变化的稳定性，从而说明此逆动力学控制方法可以得到理想的控制电压.

但是把控制电压施加到结构上得到的梁末端位移与预想控制结果的对比，才能验证所求得控制电压是否有效.因此下一步将证明控制电压的有效性.(这里取衰减率为一常数0.5，得到了控制电压，实际中可取不同衰减率，求解控制电压.)

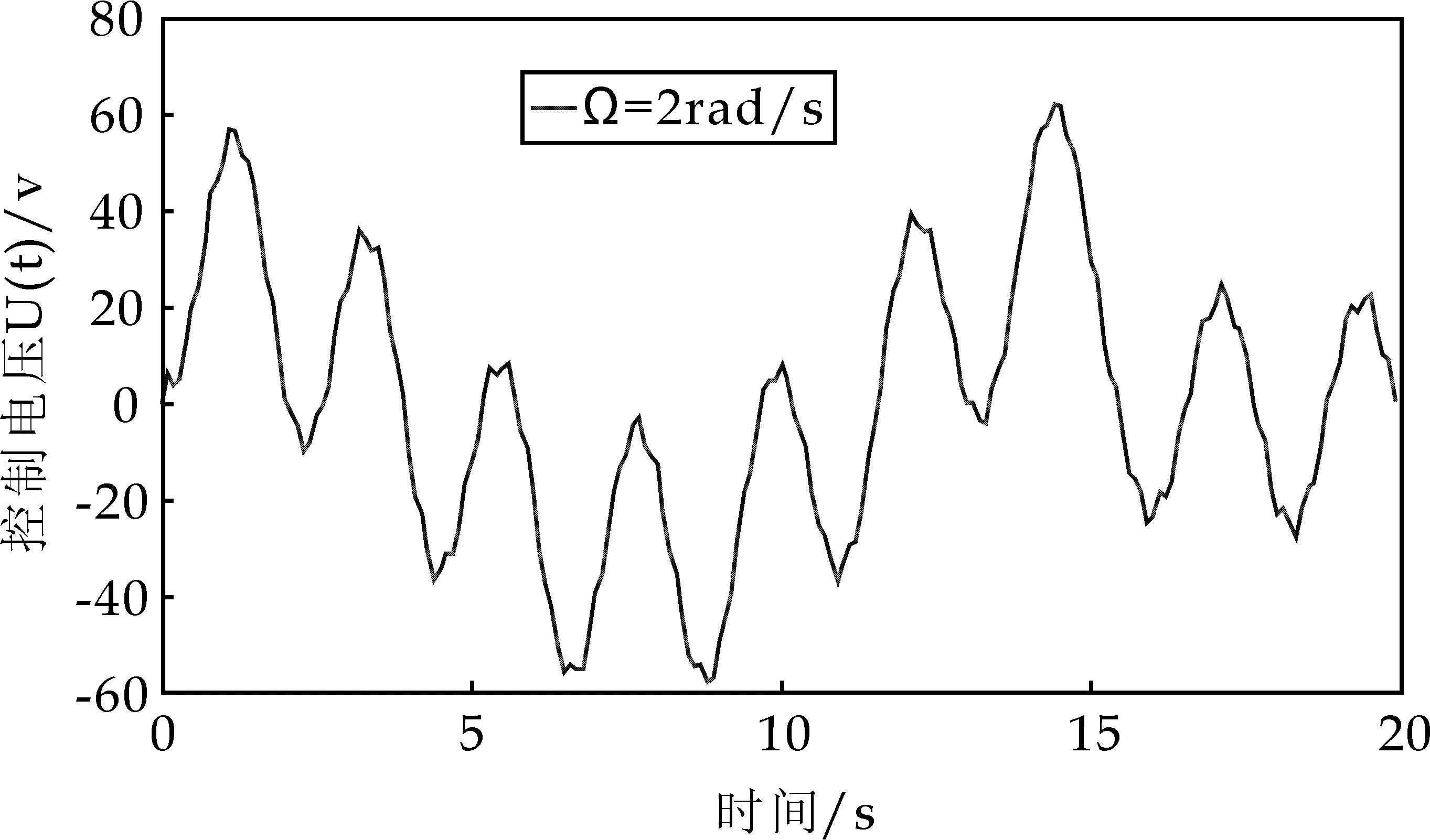
图6 控制电压时程曲线

2.3 控制电压的验证

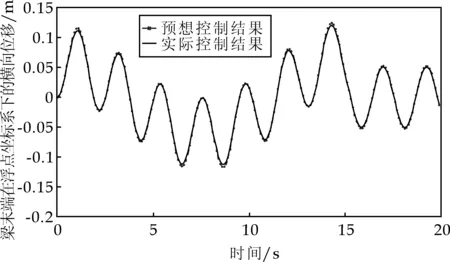
图7 实际与预想结果对比

为了该控制电压的有效性及动力学模型的正确性，将所求的控制电压回代动力学模型(12)，可得实际梁末端横向位移与预想结果的对比，如图7所示，误差为3.3%，从而可得知此逆动力学控制方法的正确可行性，并且验证了本文所得RPLCB梁模型的正确性.该压电智能结构只用平铺压电层来作为作动器，而没有传感器，同样实现了较好的控制效果，这也是一种结构的优化.

3 结束语

本文针对做旋转运动的柔性悬臂梁[9]，在梁表面平铺压电层作为作动器，建立一种柔性旋转压电层合悬臂梁模型.利用有限元法进行柔性RPLCB梁的机电耦合动力学建模，并仿真算出梁末端的响应.然后取一梁末端位移的预想衰减率，根据预想控制结果求出控制电压，即逆动力学控制方法.再把求出的控制电压回代动力学方程与预想控制结果对比，验证了该逆动力学控制方法正确性.所得结论如下：

(1)通过有限元法，考虑了压电层电场效应，建立了做大范围旋转运动平铺压电层柔性悬臂梁的一次耦合动力学模型.

(2)对动力学模型进行求解，得到该RPLCB梁上任意一点在非惯性系下，所取时间点上的位移的数值解.对两个稳定转速下的梁末端位移、速度、加速度进行仿真分析，发现转速高的情况下，数值稳定性小，这是由系统非线性导致的.

(3)通常对柔性梁的主动控制是一种闭环控制系统，是以压电传感器来把感应信号作为控制函数，使得作动器获得控制电压.这样的系统复杂而且存在时滞性.鉴于此，本文是先得到RPLCB梁的响应特性，然后根据预想控制结果逆求解出控制电压，施加给结构，就可以得到理想的控制结果，即一种逆动力学开环控制方法，省去了传感器，控制效果能达到预期效果，为压电智能梁设计提供了一种参考方法.

[1] Yoo H H,Ryan R R,Scott R A.Dynamics of flexible beams undergoing overall motions[J].Journal of Sound and Vibration,1995,181(2):261-278.

[2] 刘锦阳,洪嘉振.刚-柔耦合动力学系统的建模理论研究[J].力学学报.2002,34(3):408-415.

[3] 邓峰岩,和兴锁,李 亮,等.计及变形耦合项的平面柔性梁动力学建模及频率分析[J].振动工程学报,2006,19(1):75-80.

[4] 董兴建，孟 光.压电悬臂梁的动力学建模与主动控制[J].振动与冲击，2005,24(6):54-64.

[5] 钟美法.压电层合板的有限元分析及其精细振动控制算法的研究[D].西安：西北工业大学，2010.

[6] 姚林晓.旋转柔性智能结构分析与振动控制研究[D].西安：西北工业大学，2007.

[7] W J Manning,A R Plummer,M C Levesely.Vibration control of a flexible beam with integrated actuators and sensors[J].Smart Mater,Struct,2000,9:932-939.

[8] Crawley E F,Luis J.Use of piezoelectric actuator as elements of intelligent structures[J].Aiaa Journal,1987,25(10):1 373 -1 385.

[9] Zhang Juan,Shu Yafeng,Bai Bin.Dynamic modeling on smart flexible beam with large overall planar motion[J].Applied Mechanics and Materials,2013,387:147-153.

[10] 吴大方,刘安成,麦汉超,等.压电智能柔性梁振动主动控制研究[J].北京航空航天大学学报,2004,30(2):160-163.

[11] 方建士,章定国.旋转悬臂梁的刚柔耦合动力学建模与频率分析[J].计算力学学报,2012,29(3):333-338.

[12] J Chung,Yoo H H.Dynamic analysis of a rotating cantilever beam by using the finite method[J].Journal of Sound and Vibration,2002,249(1):147-164.

[13] 陆佑方.柔性多体系统动力学[M].北京:高等教育出版社,1996.

[14] 王矜奉，苏文斌，王春明,等.压电振动理论及应用[M].北京：科学出版社，2011.

[15] 杨 辉.刚-柔耦合动力学系统的建模理论与实验研究[D].上海:上海交通大学,2002.

[16] 刘炳妹，刘立山.二阶方程组解的存在唯一性[J].工程数学学报,2007,24(4),757-761.