基于遗传算法的弧面凸轮特征曲线优化及三维建模

田晓蕊, 曹巨江, 王波波

(1.陕西科技大学 设计与艺术学院, 陕西 西安 710021； 2.陕西科技大学 机电工程学院， 陕西 西安 710021)

0 引言

凸轮机构因其具有传动、导向和控制等功能，广泛用于包装、轻纺、印刷、食品、汽车等行业自动机械中.作为自动机械核心部件的凸轮机构必须具有优良的凸轮曲线，凸轮曲线的优良与否直接影响凸轮机构的精度、效率和寿命[1].

弧面凸轮主要用于各种需要高速传动或分度的自动机械中.该机构类似于蜗轮蜗杆装置，相当于蜗杆的凸轮装置在相当行星轮的周边上，输出轴较大.它将蜗轮蜗杆的摩擦副传动改为滚动副传动，由于减少了摩擦传动引起的能量消耗和磨损，所以大大提高了传动效率.弧面凸轮还具有体积小、重量轻、传动效率高、寿命长等特点，故在高速高精度及高效率场合得到广泛应用.

然而弧面凸轮的轮廓曲线属于不可展曲面，利用传统的图解法很难将其作出.一些学者提出一些利用实测凸轮轮廓线进行反求的方法.例如应用拉格朗日五点数值微分法，利用测绘到的极坐标反求出凸轮机构从动件的运动规律；利用三次样条差值的方法；利用B样条反求从动件运动规律.以上文献对凸轮的反求研究主要集中在样条曲线插值或拟合上.插值即要求曲线通过所有的测试点，拟合只需反映数据的趋势，并不需要经过各个测试点，常用的拟合方法有多项式拟合、最小二乘、样条函数拟合.该类拟合问题最终可以转化为非线性最小二乘求解问题.利用多元函数下山单纯行法、多元函数变尺度法、多元函数共轭梯度法、L-M型方法、G-N迭代或拟牛顿方法都可以解决此类问题.该类算法是在需要搜索空间中一个初始点按照某一确定的规则不断地寻找下一个迭代点.由于充分利用了问题本身提供的信息，此类算法具有一定的针对性，搜索速度快、局部寻优能力强，然而这类算法容易陷入局部极小值，找到的结果可能并不是问题的全局最优解[2].

本文提出一种基于遗传算法的弧面凸轮特征曲线反求优化方法，并在已知从动件运动规律的基础上利用三维软件UG对弧面凸轮进行了三维建模，更加直观地反映了二维不能表现的特征.该方法不失一般性，可以在其他凸轮曲线的设计中得到应用.

1 弧面凸轮特征曲线

目前创造的数十种特性优秀的凸轮曲线，将其恰当组合能满足各种场合的要求.凸轮从动件的运动规律(特征曲线)常用的有修正正弦曲线、修正梯形曲线和修正等速曲线等.其中简谐梯形运动规律曲线兼有简谐运动规律在两端连续及梯形运动规律最大加速度低的优点，被很多场合采用.当取不同的值时，可得到修正梯形、修正正弦和修正等速等多种运动规律曲线.故简谐梯形通用凸轮曲线的优劣主要反映在无量纲时间的选取和设计是否满足实际需要.

本文选取从动件运动规律为简谐梯形通用运动规律曲线，该曲线是在修正等加速运动规律曲线的两端各加上一段简谐曲线作为过渡，以无因次时间为横轴，无因次加速度为纵轴，如图(1)所示,加速度的表达式如下[3-7].

图1 简谐梯形通用曲线

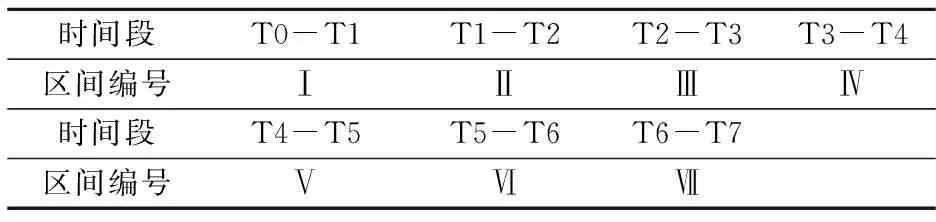
时间段T0-T1T1-T2T2-T3T3-T4区间编号ⅠⅡⅢⅣ时间段T4-T5T5-T6T6-T7区间编号ⅤⅥⅦ

将其运动规律划分七个区间:

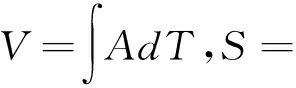
2 基于遗传算法的特征曲线反求优化

2.1 遗传算法原理

遗传算法是以自然选择和遗传理论作为理论基础，以“适者生存，优胜劣汰”为原则，仿照生物进化过程与机制求解问题的自组织与自适应的人工智能技术.该方法主要特点是对结构对象进行直接操作，不存在求导和函数连续性的限定；具有内在的隐并行性和更好的全局寻优能力；采用概率化的寻优方法，采用简单的编码技术来表示各种复杂的结构，并通过对一组编码进行简单的遗传操作和优胜劣汰的自然选择来自适应地指导学习和确定搜索的方向，不需要确定规则.由于这种用种群的方式组织搜索，能够同时搜索解空间的多个域，特别适合大规模并行计算.该方法被人们广泛的应用于组合优化、机器学习、信号处理、自适应控制和人工生命等领域[8-11].

2.2 遗传算法的运算流程

遗传算法模拟了自然选择和遗传中发生的复制、交叉和变异等现象，从一个初始种群出发，通过随机选择、交叉和变异操作，产生一群更适应环境的个体，是群体进化到搜索空间中越来越好的区域，这样一代代的不断的繁衍进化，最后收敛到一群更适应环境的个体，求得问题的最优解.执行的流程图如图2所示.

图2 遗传算法执行流程

2.3 基于遗传算法的特征曲线优化

遗传算法的这些优点可以应用在对凸轮曲线的反求优化中，具体操作步骤如下：

Step1:编码

因为Ti∈[0,1],T0=0,T7=1,因此将T1,T2,T3,T4,T5,T6作为独立的随机变量，它们中每一个Ti为一个基因片段，这些基因片段的一个组合为一条染色体.

Step2:初始群体的生成

遗传算法的初始种群为随机生成，首先随机生成N个串结构数据,随机生成N个个体作为初始群体P(0)开始迭代.设置进化代数计数器t=O；设置最大进化代数T；N∈[10,1 000],N∈N*[12].

Step3:适应度值评价检测

Step4:选择

将选择算子作用于群体,根据适应度函数值的大小排序,选取适应度高的个体进行下一步的操作.

Step5:交叉

将交叉算子作用于群体,交叉操作以交叉概率随机选取群体中的个体，并在随机生成的位置进行交叉.交叉概率ai控制着交叉操作被使用的频度.较大的交叉概率可增强遗传算法开辟新的搜索区域的能力,但高性能的模式遭到破坏的可能性增大;若交叉概率太低,遗传算法搜索可能陷入迟钝状态.一般取值从0.25到1.00之间.

Step6:变异

变异在遗传算法中属于辅助性的搜索操作,它的主要目的是维持解群体的多样性.通常取变异概率Pm为0.001左右.

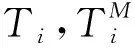
Step7：

由选择策略选出种群规模大小构成下一代种群，令k=k+1转向步骤3.

2.4 实例分析

要求设计的凸轮曲线经过表2中的点，其中T表示无因次时间，S表示无因次位移.并且要求满足特性要求：[Am]=4,858；[Vm]≤1.823；加速段较减速段短.

求：T0,T1,T2,T3,T4,T5,T6,T7

表2 设计要求的点的坐标

优化问题三要素为决策变量、目标函数和约束条件.

为了问题的求解简单，应当尽可能减少决策变量的个数，且要求这些变量彼此是相互独立的.在本问题中可以将无量纲时间Ti看做一个向量，用矩阵表示为T=(T0,T1,T2,T3,T4,T5,T6,T7)T作为优化变量，根据实际情况选取八个全部Ti或其中多个Ti作为决策变量，当给这些变量赋值时，每一组值都是该优化问题的一组解.

约束条件指对变量间需遵循的限制条件，即目标函数的可行域.约束条件不是任意的，是根据工程实际的限制条件，约束条件一般为边界约束和性能约束，表达式一般有等式约束和非等式约束，具体形式如下：

gi≥0,i=1,2,3,…,n.

当不等式约束为这种情况是两边乘以-1，统一取gi≤0形式.

目标函数是所关心的目标与相关因素的函数关系，通常是某一问题需要最优(最大或最小)的那个目标函数的表达式，是决策变量的函数，它是评价设计方案优劣的标准，本问题可以抽象的记做f(T).在选取目标函数的时候可以是单目标函数,也可以是多目标函数，具体问题时可以选取体积、质量、效率、可靠性、承载能力、成本作为优化目标，也可以选择系统的动态响应如速度、加速度(最大加速度)或加速度均方根值等动载荷，噪声、模态柔度、模态阻尼比等动态性能作为优化目标.由于在凸轮机构优化时，大部分是非线性规划，故此处采用非线性规划方法求解.遗传算法在解决此类非线性问题中较其他方法有优越性.

根据上述的遗传算法操作步骤，选取初始种群p(0)=12，迭代步数终止于600步，交叉概率取0.65，变异概率为0.001.随机变量为T=(T1,T2,T3,T4,T5,T6)T，由要求可知等式约束：Am-4.858=0.

不等式约束为：

以固定点的理论位移和期望位移之间的差值的平方和最小值为适应度函数具体建模如下：

fit(f(T))=

图3为经过遗传算法优化求得的弧面凸轮特征曲线图，表3为最终优化得到的数值.

图3 优化曲线图

时间或特征优化取值T10.063 5T20.332 1T30.498 9T40.511T50.702 1T60.934 2Am4.858Vm1.816 5

由图表可知，该弧面凸轮特征曲线的最大加速度为4.858；最大速度为1.816 5在要求的[Am]<1.823范围之内，并且可以看出加速段开始于T=0，结束于T=0.48时，减速段开始于T=0.51，结束于T=1时，加速段较减速段小.设计的特征曲线满足设计要求.

将表2中得到的T1,T2,T3,T4,T5,T6值以及T0=0,T7=1代入加速度A的表达式中即可得到加速度曲线，分别积分一次、两次得到速度曲线和位移曲线.具体代入及积分过程在这里不再赘述.

3 基于UG的三维建模[13-15]

UG NX软件具有强大的参数化建模功能以及曲面造型功能.弧面凸轮的理论廓面属于直纹面，可将直纹面参数化，在UG中完成其参数化三维建模.以下对建模过程作以简述.

(1)在三维UG软件，利用上文得到弧面凸轮特征曲线和参数表达式，生成样条曲线如图4所示.

图4 弧面凸轮曲线图

(2)利用直纹面及弧面凸轮廓面相关理论及UG的曲面造型工具，得到弧面凸轮工作廓面如图5所示.

图5 弧面凸轮工作廓面图

(3)绘制凸轮基体草图，利用回转命令完成凸轮基体造型，通过缝合以及求和命令，得到完整的弧面凸轮三维模型如图6所示.

图6 弧面凸轮三维图

(4)建立转盘模型如图7所示.(一般实际弧面凸轮机构中从动件滚子数量不超过12个，此处仅为转盘构造说明.)

图7 弧面凸轮转盘图

(5)最后进行装配，得到完整的弧面凸轮机构如图8所示，也可以利用该模型进行仿真，验证上文得到的结果.

图8 弧面凸轮机构装配图

4 结束语

本文提出一种利用遗传算法的优点有效的解决了弧面凸轮曲面不可展时的设计方法.在该种方法中由优化目标函数转化来的适应度函数的选取十分重要，适应度函数的选取直接反应了设计的目标，强调的是注重哪个方面的因素.为了全面的展现弧面凸轮的特征，本文根据上述方法得到的结果利用UG建立了弧面凸轮的三维模型，得到了工程需要的结果.后面可进一步研究动态的仿真，不同

适应度函数对最终结果的影响.该方法可以用来设计其他凸轮曲线，很值得进一步研究.

[1] 彭国勋,肖正扬.自动机械的凸轮机构设计[M].北京：机械工业出版社，1990.

[2] 董正平，傅燕明.印刷机械中凸轮机构的反求设计[J].机械设计与研究，2003，19(4):72-75.

[3] 杨玉琥,姚燕安，张 策，等.跃度连续的通用简谐梯形组合凸轮曲线的参数优化[J].大连轻工业学院学报,1995，14(3)：42-45.

[4] 张高峰，杨世平，陈华章．弧面分度凸轮机构的研究与展望[J]．机械传动，2003，27(3)：1-4.

[5] 刘言松，贺 炜，唐学飞，等．弧面分度凸轮三维实体模型的建立[J]．组合机床与自动化加工技术，2004(6)：36-37.

[6] 杨 玮，曹巨江．复杂弧面凸轮曲率和应力分析及其CAD[J].机械设计与制造，2002，31(2)：11-13.

[7] 陶学恒，王其超，肖止扬．弧面分度凸轮机构的运动几何特性分析[J].机械设计，1997(10)：21-23 .

[8] 王富民，张 扬，田社平.遗传算法与惩罚函数法在机械优化设计中的应用[J].中国计量学院学报，2004,15(4)：290-293.

[9] 张聚梅,王洪伦.基于遗传算法和模拟退火算法的B样条曲线拟合[J].计算机科学与工程,2011，33(3),191-193 .

[10] 孙增圻.智能控制理论与技术[M].北京：清华大学出版社,1997.

[11] 樊重俊，王浣尘．遗传算法的改进与应用[J]．上海交通大学学报，1998，32(12)：128-131.

[12] 何大阔，王福利．遗传算法初始种群与操作参数的均匀设计[J].东北大学学报(自然科学版)，2005,26(9)：828-831.

[13] 白雪峰，尚 锐，李生元，等.基于UG的弧面分度凸轮逆向CAD/CAM研究[J].辽宁工业大学学报，2009，29(6):399-402.

[14] 曹巨江，李龙刚，吕凯归，等.基于UG NX6.0的弧面分度凸轮三维实体建模与仿真加工[J].机械设计与制造，2011(1):169-171.

[15] 刘加利，王好臣，李玉胜，等.直纹面在弧面凸轮设计中的应用[J].山东理工大学学报(自然科学版)，2006,20(5):60-63.