GPS/GLONASS组合精密单点定位

刘站科，付文举，黄观文，李 昕

(1.武汉大学测绘学院，湖北武汉 430079；2.国家测绘地理信息局第一大地测量队，陕西西安710054；3.长安大学地质工程与测绘学院，陕西西安 710054；4.国家测绘地理信息局第一地理信息制图院，陕西西安 710054)

GPS/GLONASS组合精密单点定位

刘站科1，2，付文举3，黄观文3，李 昕4

(1.武汉大学测绘学院，湖北武汉 430079；2.国家测绘地理信息局第一大地测量队，陕西西安710054；3.长安大学地质工程与测绘学院，陕西西安 710054；4.国家测绘地理信息局第一地理信息制图院，陕西西安 710054)

为了改善传统GPS/GLONASS组合精密单点定位的法方程，推导出一种基于等价消参法的融合法方程。该融合法方程是由GPS系统的法方程和GLONASS系统的法方程进行消除参数叠加得到，既易于实现GPS/GLONASS系统组合单点定位，也便于进行单系统定位的切换。理论证明，基于等价消参法的融合法方程和传统的组合法方程是等价的。程序设计和算例分析显示，基于等价消参法的融合法方程在GPS/GLONASS组合系统精密单点定位和单系统定位转换方面比传统的组合法方程具有更高的效率。最后，利用实测算例分析了GPS/GLONASS组合精密单点定位的定位精度。

GPS；GLONASS；参数消化；精密单点定位

一、引 言

目前，基于GPS的精密单点定位技术已很成熟，实现了静态mm-cm级、动态cm-dm级的定位精度[1-6]。但是，随着GLONASS系统的现代化，GPS和GLONASS组合精密单点定位技术具有单系统定位难以比拟的优势，如果利用更多卫星的观测数据，可获得更高精度和更可靠的定位结果，并且其在连续性、可用性和定位效率上更有优势等[7-11]。

综合以上原因，考虑到目前很多学者直接对GLONASS和GPS观测方程构建组合的法方程，虽然这种方法简单易懂、易于实现，但是在多系统定位和单系统定位间转换较为困难。为了易于在多系统定位和单系统定位间转换，以及提高定位的效率，本文首先分别建立GPS系统和GLONASS系统的法方程，然后基于等价消参法进行叠加得到融合法方程，最后采用序贯最小二乘，实现了GPS和GLONASS组合精密单点定位，并通过算例，得出了一些有意义的结论。

二、精密单点定位原理

精密单点定位的伪距观测方程为

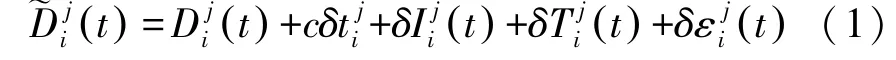
精密单点定位的载波观测方程为

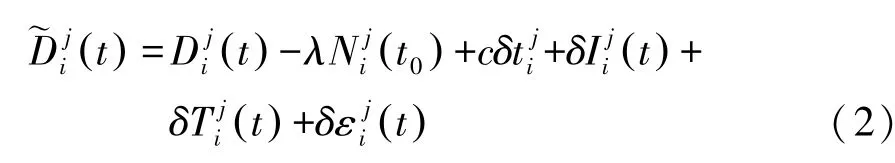
线性化后的精密单点定位伪距观测方程为

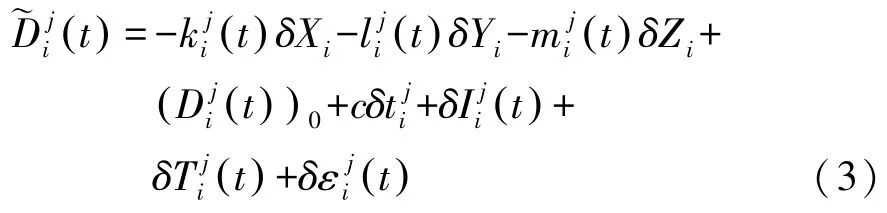
线性化后的精密单点定位载波观测方程为

三、基于参数消化法的GPS/GLONASS组合精密单点定位

1.传统法方程组合形式

采用无电离层组合观测值，得到GPS和GLONASS的观测方程组，可以得到法方程如下

式中，Pg、Lg分别为GPS伪距和载波无电离层组合观测值向量；εgp、εgl为 GPS观测模型残差向量；Ag为GPS接收机钟差系数矩阵；Bg为测站三维位置和对流层湿延迟参数系数矩阵；Ig为GPS模糊度参数系数矩阵；Pr、Lr为GLONASS伪距和载波无电离层组合观测值向量；εrp、εrl为GLONASS观测模型残差向量；Ar为GLONASS接收机钟差系数矩阵；Br为测站三维位置和对流层湿延迟参数系数矩阵；Ir为GLONASS模糊度参数系数矩阵。

2.基于消参法的融合法方程

由于传统的法方程无法满足在GPS/GLONASS组合定位和单系统定位之间自由切换的要求，本文推导了基于参数消化法的融合法方程，即分别计算单系统的法方程，然后采用参数消化的原理得到融合法方程。考虑到静态定位和动态定位两种模式，分别推导了两种情况下的融合法方程形式。

(1)基于静态定位的融合法方程

采用无电离层组合观测值，得到静态定位GPS系统的法方程

消去GLONASS接收机钟差和系统时差参数

由式(7)和式(9)叠加得到静态GPS/GLONASS组合定位的融合法方程为

(2)基于动态定位的融合法方程

采用无电离层组合观测值，得到动态定位GPS系统的法方程为

由式(14)和式(18)叠加得到组合法方程

3.基于消参法的组合定位实现流程

为了直观地理解消参法的思想，以及动态定位和静态定位的实现流程，GPS和GLONASS组合动态精密单点定位和静态精密单点定位的实现流程分别如图1、图2所示。

图1 静态定位的算法流程

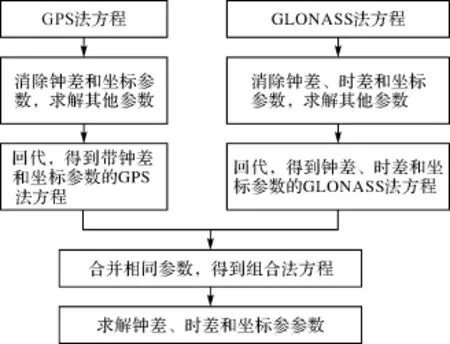
图2 动态定位的算法流程

四、实例分析

为了实现基于消参法的GPS/GLONASS组合静态和动态定位，同时分析GPS和GLONASS组合精密单点定位的定位精度，本文采用欧洲航天控制中心(ESOC)提供的最终轨道和钟差产品，统计了大量IGS站的定位精度。由于篇幅限制，本文仅给出10个IGS站2012年1月3日的静态定位结果及其中AUCK站的动态定位结果。如图3、表1所示，其中G代表GPS，R代表GLONASS。

图3 ENU方向的静态定位精度

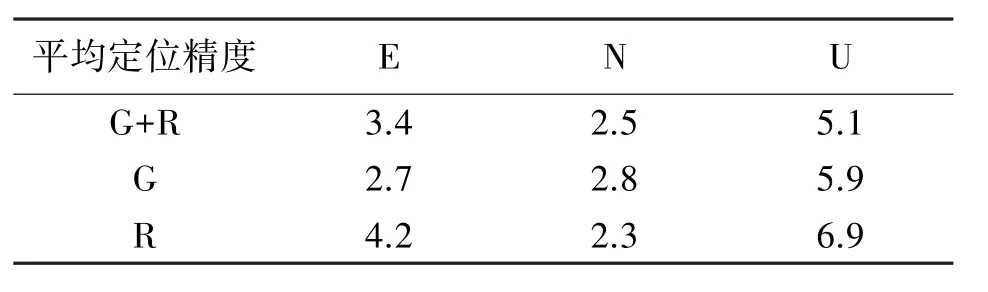
表1 ENU方向静态定位的平均精度 mm

从图3和表1中，对比 E、N、U方向上 GPS/ GLONASS、GPS和GLONASS静态定位精度可以发现：在E方向上，GPS/GLONASS组合静态定位精度高于GLONASS定位精度但低于GPS定位精度；在N方向上，GPS/GLONASS组合静态定位精度高于GPS定位精度但低于GLONASS定位精度；而在U方向上，GPS/GLONASS组合静态定位精度最高。由此可见，GPS和GLONASS组合静态定位的精度比单系统定位精度要高且稳定。

为了便于分析GPS和GLONASS组合动态定位的收敛时间和收敛后的定位精度，本文分析了2012年1月3日AUCK站的动态定位精度。考虑到定位收敛时间，将24 h的定位结果分解为第1 h和后23 h共两个时段，分别作图比较GPS/GLONASS组合动态及单系统的定位精度，如图4、图5所示。

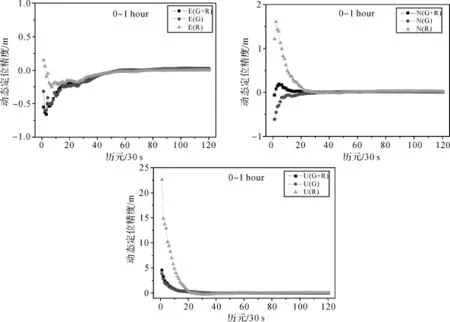
图4 第1 h ENU方向AUCK站动态定位精度

图5 后23 h ENU方向AUCK站动态定位精度

为了比较GPS/GLONASS组合动态定位和单系统的精度，本文统计了AUCK站动态定位后23 h的平均定位精度，见表2。

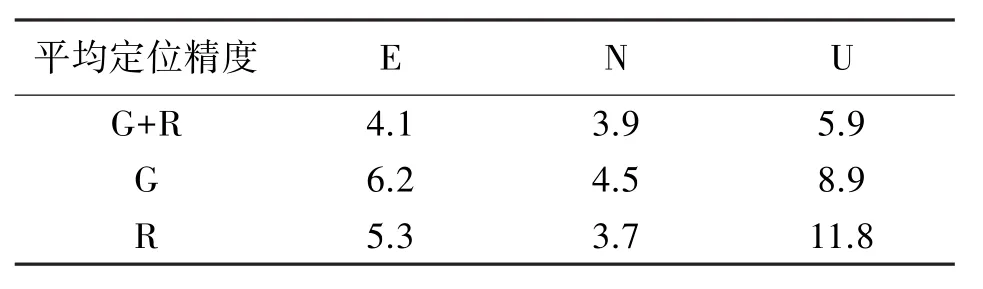
表2 ENU方向AUCK站的动态定位平均精度 mm

从图4可以看出，在E方向，GPS/GLONASS组合动态定位和单系统动态定位的收敛速度较为一致，收敛时间为20 min；而在N和U方向上，GPS/ GLONASS组合动态定位的收敛速度和GPS系统动态定位相差不大，收敛时间为5 min，优于GLONASS动态定位的收敛速度，其收敛时间为10 min。

从图5和表2可以看出，在动态定位收敛后，在E和N方向上，GPS/GLONASS组合动态定位和单系统动态定位的定位精度均较小；而在U方向上，GLONASS动态定位精度最差，其均方根中误差达到11.8 mm，而GPS/GLONASS组合动态定位精度最高，其平均定位精度为5.9 mm。可见，GPS/GLONASS组合动态定位的精度比单系统定位较为稳定。

五、结 论

本文推导了基于消参法的GPS/GLONASS组合静态定位和动态定位融合法方程模型，并利用2012年1月3日10个IGS站的观测数据，以及欧洲航天控制中心(ESOC)提供的最终轨道和钟差文件，分析了GPS/GLONASS组合静态定位和动态定位的精度，得到了以下结论和建议：

1)基于消参法的融合法方程模型在多系统定位和单系统定位转换方面比传统的组合法方程更具有优越性。

2)在静态定位方面，E方向上，GPS/GLONASS定位精度高于GLONASS，但低于GPS；N方向上，GPS/GLONASS定位精度高于 GPS，而低于 GLONASS；在U方向上，GPS/GLONASS组合静态定位精度最高。

3)在动态定位的收敛速度方面，E方向上，GPS/GLONASS组合动态定位和单系统动态定位的收敛时间为20 min；N和U方向上，GPS/GLONASS定位的收敛时间和GPS系统均为5 min，优于收敛时间为10 min的GLONASS系统。

4)在动态定位精度方面，在E和N方向上，GPS/GLONASS和单系统动态定位的定位精度均较小；而在U方向上，GLONASS动态定位精度最差，而GPS/GLONASS组合动态定位精度最高。

[1] 张勤，李家权.GPS测量原理及应用[M].北京：科学出版社，2005.

[2] HUANG Guanwen，ZHANG Qin，LI Hongtao，et al.Research on Quality Variation of GPS Satellite Clocks Onorbit Using IGS Clock Products[J].Advances in Space Research，2012，doi：10.1016/j.asr.2012.09.041

[3] 孟祥广，郭际明.GPS/GLONASS及其组合精密单点定位研究[J].武汉大学学报：信息科学版，2010，35 (12)：1409-1413.

[4] 蔡昌盛，朱建军，戴吾蛟，等.GPS/GLONASS组合精密单点定位模型及结果分析[J].武汉大学学报：信息科学版，2011，36(12)：1474-1417.

[5] 张小红，郭斐，李星星，等.GPS/GLONASS组合精密单点定位研究[J].武汉大学学报：信息科学版，2010，35(1)：9-12.

[6] 蔡昌盛，戴吾蛟，匡翠林，等.利用UofC消电离层组合的GPS/GLONASS精密单点定位研究[J].武汉大学学报：信息科学版，2012，37(7)：827-830.

[7] CAI Changsheng，GAO Yang.Performance Analysis of Precise Point Positioning Based on Combined GPS and GLONASS[C]∥The ION GNSS 20th International Technical Meeting of the Satellite Division.Fort Worth，Texas：[s.n.]，2007.

[8] 杨元喜，李金龙，徐君毅，等.中国北斗卫星导航系统对全球 PNT用户的贡献[J].科学通报，2011，56 (21)：1734-1740.

[9] YANG Y，SONG L，XU T.Robust Estimator for Correlated Observations Based on Bifactor Equivalent Weights [J].Journal of Geodesy，2002，76(6-7)：353-358.

[10] HUANG Guanwen，ZHANG Qin.Real-time Estimation of Satellite Clock Offset Using Adaptively Robust Kalman Filter with Classified adaptive Factors[J].GPS Solution，2012，doi：10.1007/s10291-012-0254-z

[11] 王潜心，徐天河，许国昌.自适应换站算法及其在长距离机载GPS动态相对定位中的应用[J].测绘学报，2011，40(4)：429-434.

[12] 王艳东，龚健雅，黄俊韬，等.基于中国地球空间数据交换格式的数据转换方法[J].测绘学报，2000，29 (2)：142-148.

GPS/GLONASS Combined Precise Point Positioning

LIU Zhanke，FU Wenju，HUANG Guanwen，LI Xin

P228.4

B

0494-0911(2014)07-0006-05

2013-04-17

国家自然科学基金(41104022)；国家自然基金国际(地区)合作交流项目(412101043)

刘站科(1981—)，男，陕西咸阳人，博士生，工程师，研究方向为大地测量数据处理、地球重力场理论与应用。

刘站科，付文举，黄观文，等.GPS/GLONASS组合精密单点定位[J].测绘通报，2014(7)：6-10.

10.13474/j.cnki.11-2246.2014. 0213