长初级短次级六相直线感应电动机数学模型分析

吕敬高，饶金

(1. 海军驻湖南地区军事代表室，湘潭 411101； 2. 海军工程大学舰船综合电力技术国防科技重点实验室，武汉 430033）

长初级短次级六相直线感应电动机数学模型分析

吕敬高1，饶金2

(1. 海军驻湖南地区军事代表室，湘潭 411101； 2. 海军工程大学舰船综合电力技术国防科技重点实验室，武汉 430033）

基于大功率直线推进的特殊要求，设计了一种新型长初级短次级六相直线感应电动机，介绍了六相直线感应电动机的绕组结构。在此基础上，推导了六相长初级短次级直线感应电动机数学模型，分析了由电机各相端部绕组空间相对位置决定的六相直线感应电动机端部漏感的不对称规律，并与多相旋转电机端部漏感的规律进行了对比。建立了仿真模型，对电机的电磁性能进行计算。

直线感应电动机 六相 数学模型 端部漏感

0 引言

长初级短次级直线感应电动机具有结构简单、可靠性高、维护方便等固有优势，结合电力电子变频调速技术的飞速发展，近几年对长初级短次级直线感应电动机在大功率直线推进领域的应用研究越来越多[1-4]。

应用于大功率直线推进领域的直线感应电动机要求输出功率大，冗余性能高，同时现有单个电力电子功率模块的容量难以满足发射功率的需求，为此目前研究的热点集中在多定子直线感应电动机的方案，如图1所示，其结构特点是若干个相同结构的定子模块沿动子高度和宽度方向对称排布，每个定子模块均为三相绕组结构，且每个定子模块独立供电，从而解决了电力电子功率器件的容量问题和系统的冗余性问题。

在大功率交流调速领域，多相旋转感应电动机早已成为国内外学者的研究热点，取得了一系列的研究成果，并已成功应用于船舶电力推进系统中。与传统三相旋转感应电动机相比，多相旋转感应电动机具有以下优点：

1）相数增加，可降低每相功率器件的容量，避免功率器件串（并）联带来的静、动态均压（流）问题。

2）电动机相数越多，脉动转矩的频率越高且幅值越小，电动机的噪声与振动降低，运行性能得以改善。

3）系统冗余性强，提高了电动机运行的可靠性。

综上，多相直线感应电动机也是满足大功率直线推进系统需求的可行方案之一，如图2所示，并且与多定子直线感应电动机相比，具有如下优点：

1）多定子直线感应电动机各个定子模块均存在上下端部绕组，而多相直线感应电动机只存在上下一对上下端部绕组，所以多相直线感应电动机的定子高度可明显小于多定子直线感应电动机，多相直线感应电动机绕组长度也小于多定子直线感应电动机，从而降低了损耗，提高了效率。

2）多定子直线感应电动机不同高度位置的定子模块的气隙磁场耦合关系不同，多相直线感应电动机各套三相绕组气隙磁场的耦合关系基本相同。

目前对多相直线感应电动机的研究尚处于起步阶段，本文提出了一种六相长初级短次级直线感应电动机的电磁结构，推导了六相长初级短次级直线感应电动机的数学模型，分析了各相端部绕组沿电机长度方向空间相对位置的不同导致的电机端部绕组互感不对称规律，基于数学模型建立了仿真模型，对电机性能进行了仿真计算。

1 六相长初级短次级直线感应电动机绕组设计

六相直线感应电动机定子绕组由2套三相绕组构成，其绕组分布如图3所示，

定子绕组采取单层集中整距布置形式，如图4所示。

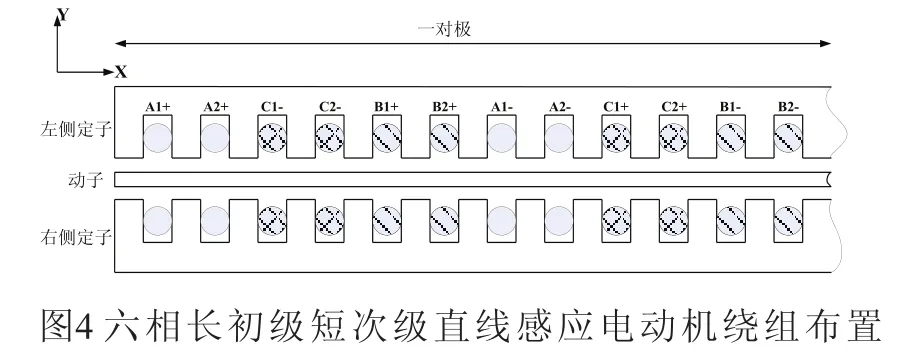
六相双边直线感应电动机的绕组结构如图5所示。

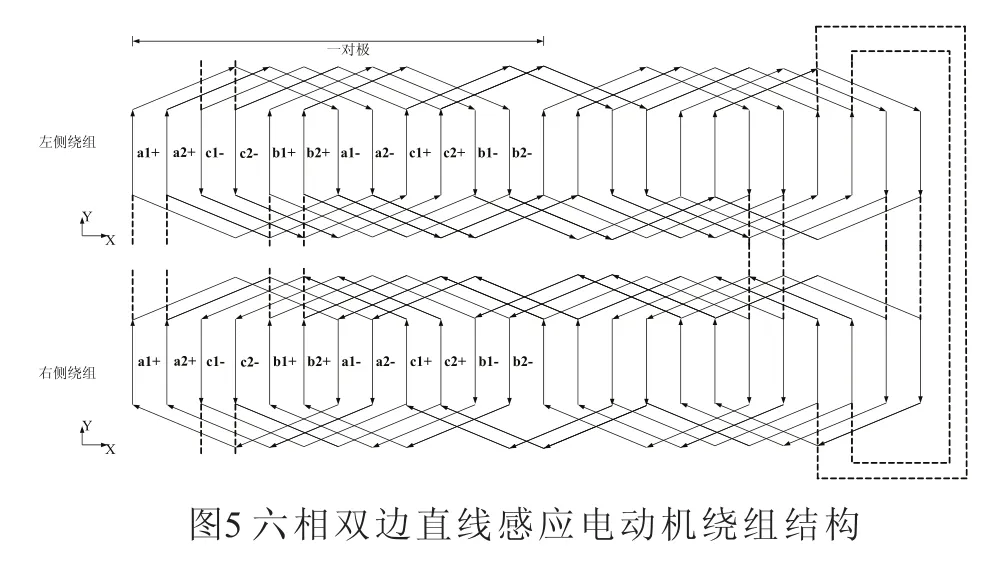
2 六相长初级短次级直线感应电动机ABC坐标系数学模型

2.1 假设条件及正方向选择

基本假设:忽略磁滞和涡流影响，铁磁饱和的影响用饱和系数考虑，不计导线的集肤效应；引入卡氏系数考虑定子开槽的影响；定子与动子之间只有空间基波磁场的耦合，即定子漏电抗与动子位置无关。

正方向选择：定、动子电路均按电动机惯例，流入电机的电流为正方向，电压降的正方向与电流的正方向一致；正方向的定、动子的电流均产

生正的磁链。

2.2 ABC坐标系数学模型

六相直线感应电机在ABC坐标系下的基本方程为：磁链方程：

电压方程：

其中磁链向量：

其中Lss为六相定子绕组之间的互感矩阵，Lsr为六相定子绕组与动子等效绕组之间的互感矩阵，Lrr为动子等效绕组之间的互感矩阵。

六相定子绕组互感矩阵Lss除了包括气隙磁场对应的主电感外，还包括槽漏感、谐波漏感和端部漏感。

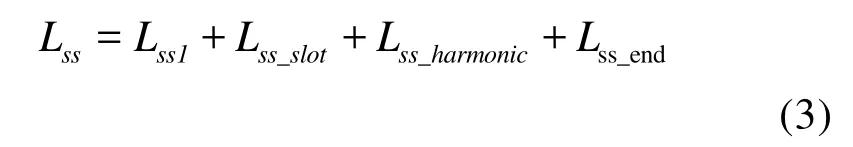
1）气隙磁场对应的电感矩阵

其中各矩阵元素为：

式(5)、(6)中，Lmm1和Lls1分别为电机每相绕组在动子覆盖部分和动子未覆盖部分气隙磁场对应的电感，上述矩阵可以看出：由气隙基波磁场产生的同一套三相绕组的自电感矩阵为对称阵，不同两套三相绕组之间的互感矩阵为循环对称阵。

2）槽漏感矩阵

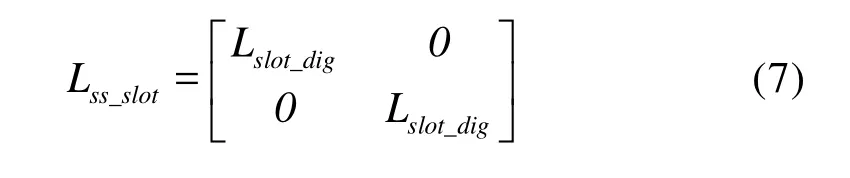
其中各矩阵元素为：

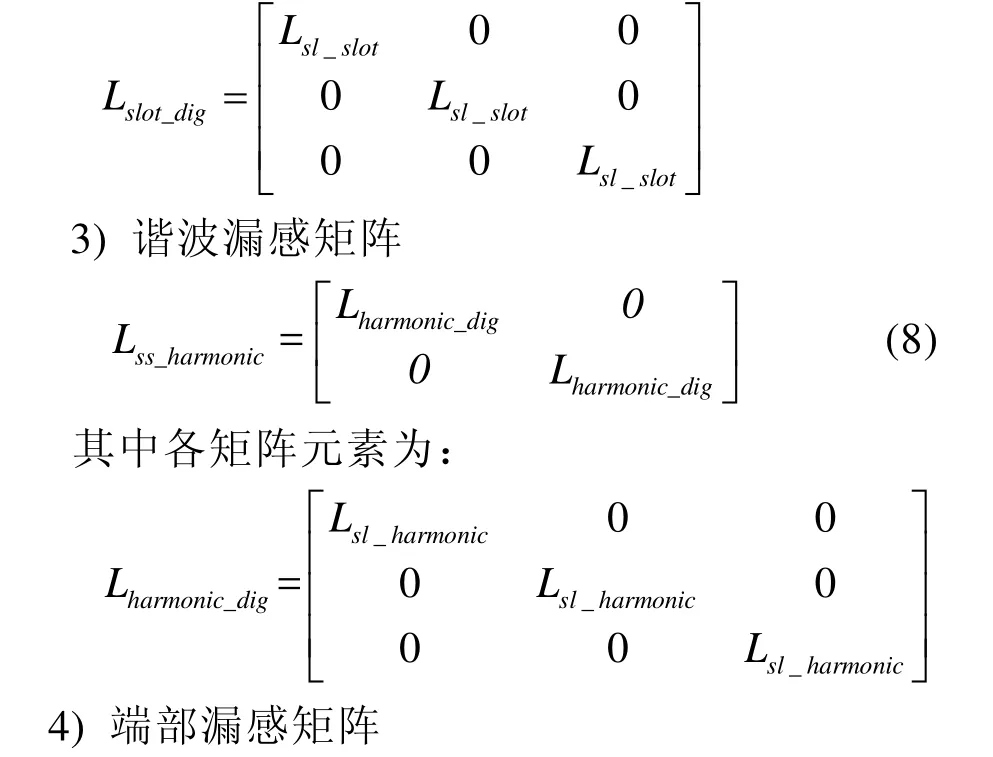
由式(10)、(11)可以发现，上述每套三相绕组的端部漏感矩阵和两套三相绕组的端部互漏感矩阵都是不对称矩阵，同一套三相绕组的端部漏感矩阵中各元素关系是：

不同两套三相绕组的端部互漏感矩阵中各元素关系是：

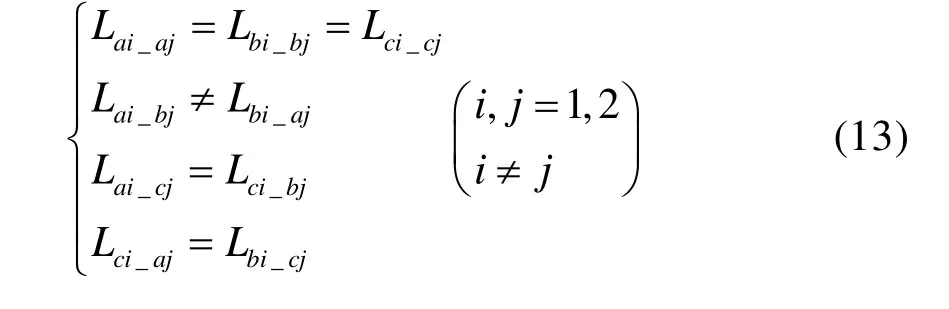
对于多相旋转电机，其同一套三相绕组的端部自漏感矩阵和两套三相绕组的端部互漏感矩阵分别如式(14)：

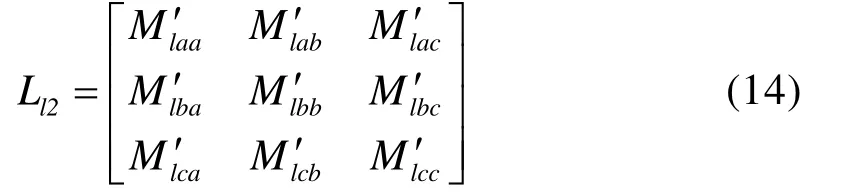
其中，同一套三相绕组的端部自漏感矩阵中各电感值的大小关系如下所示，即同一套三相绕组的各相端部自漏感相等，两相之间的端部互漏感相等。

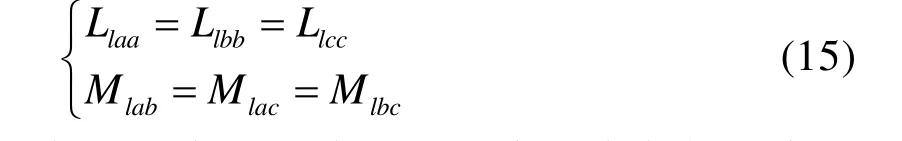
两套三相绕组的端部互漏感矩阵中各电感值的大小关系如下所示：

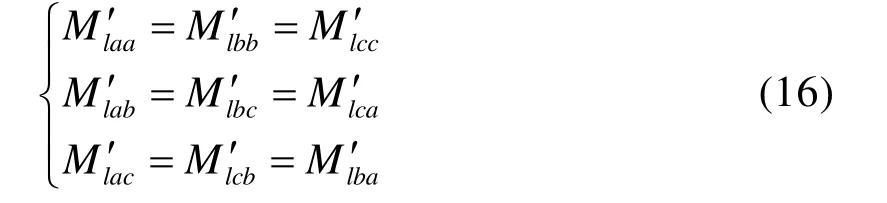
综上，可以发现六相直线感应电机各相端部漏感的规律与多相旋转电机各相端部漏感的规律不同，这是因为直线电机与旋转电机的端部绕组空间结构不同造成的。

5) 动子自感矩阵

式(19)中，θr为定子a1相绕组轴线与动子a相绕组轴线的夹角。

3 仿真结果

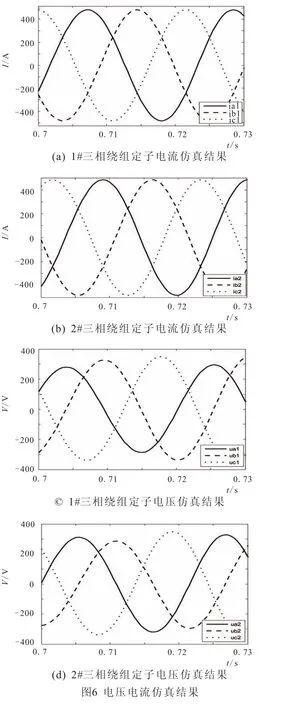
基于本文建立的十二相直线感应电机数学模型，建立对应的仿真模型，其电压、电流仿真结果如图6所示，可以发现当电机定子电流对称时，其定子电压不对称。

5 结论

本文设计了一种应用于大功率直线推进的新型六相长初级短次级直线感应电动机，在提出该六相直线感应电动机绕组结构的基础上，推导了六相长初级短次级直线感应电动机数学模型，分析了由电机各相端部绕组空间相对位置决定的六相直线感应电动机端部漏感的不对称规律，为多相直线感应电动机的设计和性能分析提供了重要参考。

[1] Bushway R R. Electromagnetic aircraft launch system development considerations [J]. IEEE Transactions on Magnetics, 2001, 37(1): 146-152.

[2] Fair H D. The science and technology of electric launch [J]. IEEE Transactions on Magnetics. 2001, 37(1): 312-316.

[3] Doyle M R, Samuel D J, Conway T. Electromagnetic aircraft launch system emals[J]. IEEE Transactions on Magnetics, 1995, 31(1): 214-217.

[4] 许金, 马伟明, 鲁军勇. 分段供电直线感应电机气隙磁场分布和互感不对称分析[J]. 中国电机工程学报, 2011, 31(15): 61-68.

[5] Patterson D, Antonello M, Charles W, et al. Design and simulation of a permanent-magnet electromagnetic aircraft launcher[J]. IEEE Transactions on Industry Applications, 2005, 41(2): 769-773.

[6] Stumberger G, Zarko D, Aydemir M, et al. Design and comparison of linear synchronous motor and induction motor for electromagnetic aircraft launch system [J]. IEEE Transactions on Magnetics, 2003, 39(5): 2513-2518.

[7] Gorazd S, Mehmet T A, Damir Z, et al. Design of a linear bulk superconductor magnet synchronous motor for electromagnetic aircraft launch systems [J]. IEEE Transactions on Applied Superconductivity, 2004, 14(1): 346-351.

[8] Meeker D C, Newman M J．Indirect vector control of a redundant linear induction motor for aircraft launch[J]．Proceedings of the IEEE, 2009, 97(11) :1768-1776.

[9] 王东, 马伟明, 郭云珺. 基于非正弦供电方式的多相感应电动机建模[J]. 电工技术学报, 2010, 25(2): 6-14.

[10] 孙俊忠, 马伟明, 吴旭升. 3/12 相双绕组发电机数学模型研究[J]. 中国电机工程学报, 2003, 23(1): 93-96.

[11] 王东, 吴新振, 马伟明. 非正弦供电十五相感应电机气隙磁势分析[J]. 中国电机工程学报, 2009, 29(15): 88-94.

Analysis of Mathematical Model of the Six-phase Linear Induction Motor with Long Primary Short Secondary

Luv Jinggao1, Rao Jin2
(1. Naval Representatives Office in Hunan, Xiangtan 411101, Hunan, China; 2. Naval University of Engineering , Wuhan 430033 , China）

Based on the requirement of high-power linear propulsion system, a novel six-phase linear induction motor(LIM) with long primary short secondary is designed, and the winding construction of six-phase LIM is presented in this paper. On the basis of this, mathematical model for this novel motor is derived, and compared with the law of the asymmetry of end-winding leakage inductance of the multi-phase rotating motor, the rule of the asymmetry of end-winding leakage inductance of the six-phase LIMs determined by the relative space position of the each phase end-winding in the motor is analyzed. Simulation model of the motor is established, and the electromagnetic properties of the motor is calculated.

linear induction motor; six-phase; mathematical model; leakage inductance

TM359.4

A

1003-4862（2014）03-0073-05

2013-09-18

饶金（1983-），男，博士研究生。研究方向：直线电机设计及控制。