一种基于磁偶极子模型的铁磁体近场计算方法

余杰，林春生，周建军

（海军工程大学兵器工程系，武汉 430033）

一种基于磁偶极子模型的铁磁体近场计算方法

余杰，林春生，周建军

（海军工程大学兵器工程系，武汉 430033）

为计算铁磁体的感应磁场，在普通磁偶极子模型的基础上，结合微元的思想，研究了微元磁偶极子模型的计算方法，推导出了空间任一点感应磁场值的精确表达式。弥补了普通磁偶极子模型不能精确计算近场源点磁场的不足。分别用普通磁偶极子模型和微元磁偶极子模型计算了圆柱形铁磁体的感应磁场，结果表明，微元磁偶极子模型计算感应磁场精确度较高，可应用于工程实际。

感应磁场 磁偶极子 微元 圆柱形铁磁体

0 引言

在设计运动载体的内部结构布局时，经常要考虑到载体内部器件的磁化问题[1]。如飞行器和磁引信制导武器等，其内部磁环境十分复杂，既有通电电流产生的磁场，又在地磁场中高速运动被磁化产生感应磁场。所以精确计算磁体的感应磁场，了解磁体的空间磁场分布规律，对于优化运动载体的结构设计，以减少其对磁测装置的影响，和为磁干扰产生设备外加铁磁屏蔽体的设计提供依据[2]，具有十分重要的意义。

目前电磁场的数值计算方法有很多，主要分为积分方程法和微分方程法[3]，结合计算机技术可以有效解决电磁场的计算问题。但是这些计算方法的前处理十分复杂，对于初学者比较难于掌握。磁偶极子模型是电磁学的基础内容，计算电磁场简单有效，方法容易掌握，在满足使用条件下，计算电磁场的精度也比较高，可以满足工程应用要求。但是磁偶极子模型要求场点距离场源点的距离远大于磁介质的线性尺寸[4]，所以在近场源点，磁偶极子模型并不适用。如何方便准确地计算磁体的近空间磁场，满足工程应用需求，是一个很有意义的问题。本文在普通的磁偶极子模型基础上，结合微元的思想，研究了微元磁偶极子模型的计算方法。

1 铁磁体的磁偶极子模型

如图1，作用于铁磁体的外磁场分量为He。对应外磁场分量分别为Hex，Hey，Hez，其产生的感应磁矩分别为Mx，My，Mz，那么：

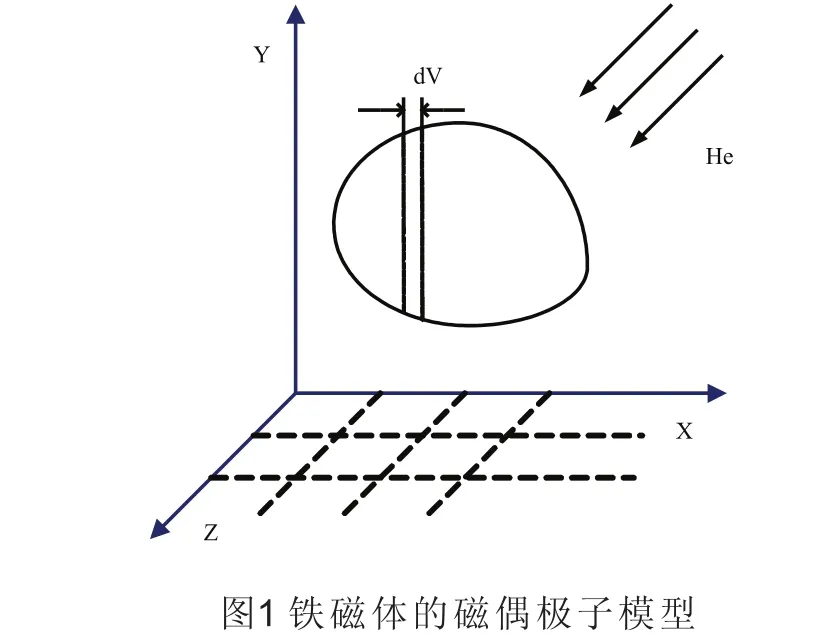
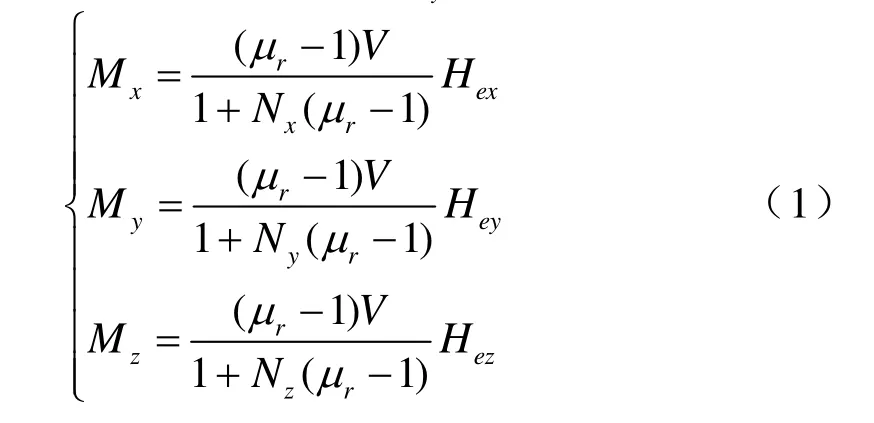
上式中Nx，Ny，Nz分别为铁磁体在X，Y，Z方向上的退磁因子，是一个确定的值，和铁磁体的形状及几何尺寸有关，可以通过实验获得。该铁磁体在空间任一点产生的磁场为：

式中，ai，bi，ci(i=x,y,z)为磁体的磁场计算系数，是已知的分布函数，和磁体的形状有关。求解上述方程组（1），（2）即得到圆柱形铁磁体在空间任一点产生的磁场强度的数值解。

2 铁磁体的微元磁偶极子模型

如图1，铁磁体在外磁场作用下被磁化，轴线上长度为dx的一段微元磁体，对应外磁场分量产生的感应磁矩为dMx，dMy，dMz，那么：

该微元磁体在空间任一点产生的磁场为：

对上述矩阵方程进行积分计算即可得到磁体在空间任一点的感应磁场强度的精确值。

3 计算实例

以圆柱形铁磁体为例（图2），由于圆柱体的对称性，只考虑外磁场在x和y方向的分量，假设分别为Hex，Hey。

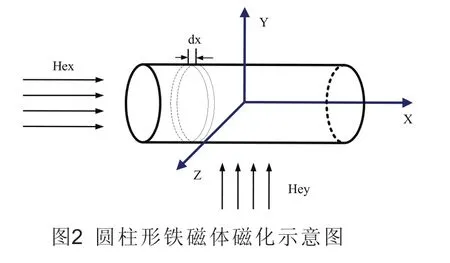
对应外磁场产生的感应磁矩为：

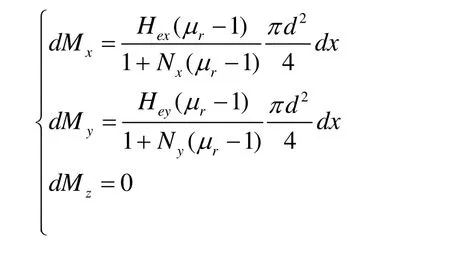
圆柱体的磁场计算系数为

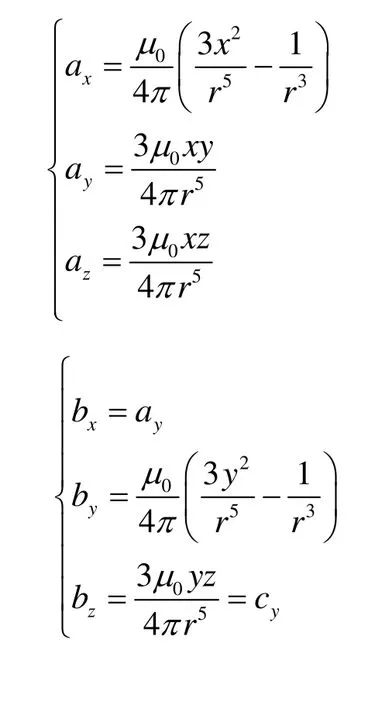
圆柱形铁磁体的退磁因子有如下的经验公式：

式中λ为圆柱体的细长比，λ=L/d。那么空间任一点感应磁场的强度为:

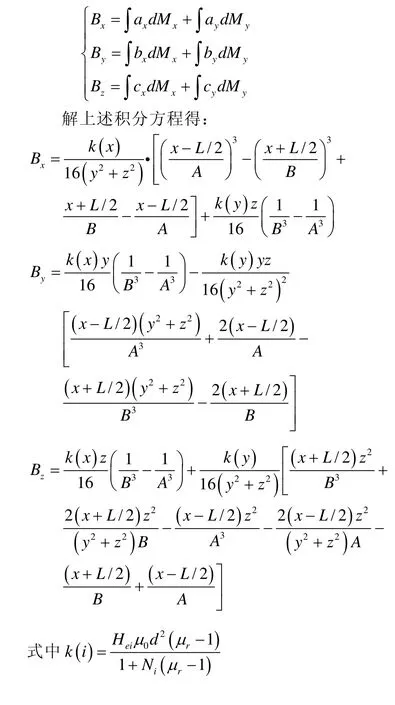
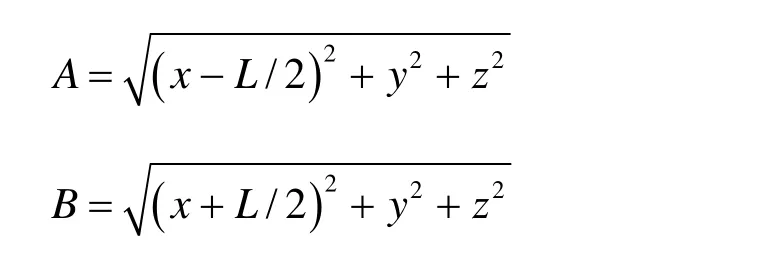
上述磁场值的求解结果已化成仅关于x，y和z的表达式，由此可见得到铁磁体空间任一点的感应磁场值的数值解的问题已解决。

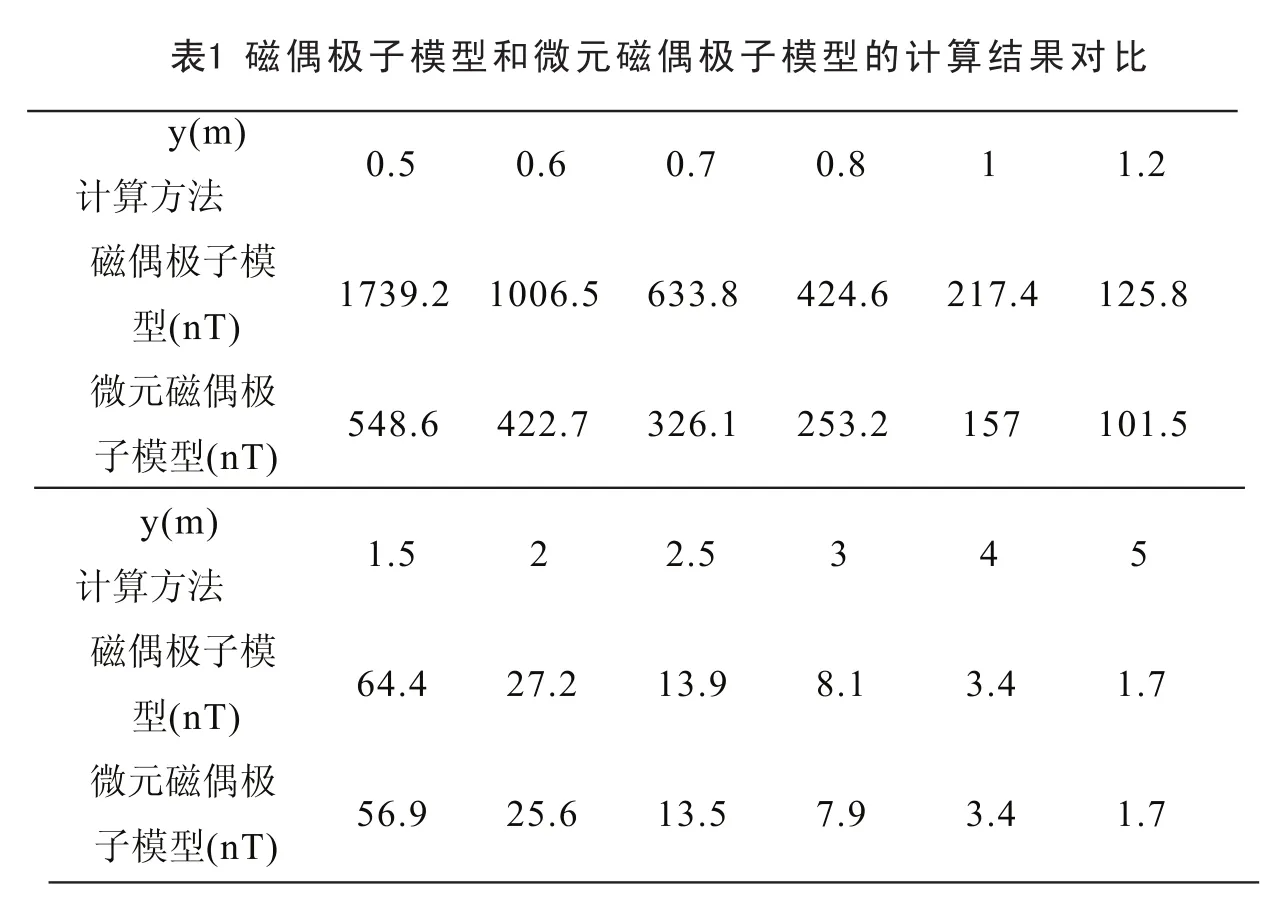
为了检验模型的准确性，分别用磁偶极子模型和微元磁偶极子模型进行计算，为不失一般性和考虑到工程应用实际，取y轴上的一列点，计算圆柱形铁磁体的感应磁场。假设圆柱形铁磁体底面直径为d=0.1m，长度为L=0.5m，且Hex=Hey=30A/m，磁体的相对磁导率为μr=50。计算结果如表1所示。

从表中可以看出，当测量点距离圆柱体较近时，本文提出的方法和磁偶极子模型计算出的结果相对误差较大；当距离铁磁体较远时，在y>2m时，相对误差已降至5%以下。出现这种结果的原因是，磁偶极子模型要求测量点到磁介质中心的距离比磁介质的线性尺寸大得多，所以在距离圆柱体较近的区域，普通的磁偶极子模型已不再满足适用条件，计算误差较大；在远离磁介质的空间内，磁偶极子模型是广泛适用的，因而可以认为计算结果是准确的。在接近圆柱体的区域，测量点到每一个微小圆柱体中心的距离相对于微小圆柱体的线性尺寸，也可认为满足磁偶极子模型的计算条件。由此可以看出，用本文使用的方法计算感应磁场精确度较高，在接近磁介质区域计算感应磁场能弥补普通磁偶极子模型的不足。

4 结论

本文在普通的磁偶极子模型基础上，结合微元的思想，提出了微元磁偶极子模型的计算方法，从理论上说可用于计算铁磁体空间全方位的磁场，算法简单，易于实现。通过对比分析，用此方法计算感应磁场精确度较高，且微元法的适用范围比较广泛，适于计算不同形状的磁体感应磁场，具有实用价值。

[1] 刘景萍,赵惠昌,黄文良. 箔条对引信的干扰研究[J].兵工学报, 2001,22(2):182 -184.

[2] 周建军,林春生,胡叶青等. 用于磁探测的铁磁屏蔽体的形状与尺寸设计[J]. 磁性材料及器件, 2012, 43(4):49 -53.

[3] 关海爽,马文阁. 电磁场数值计算新方法的研究[J].辽宁工学院学报, 2006, 26(4):230-233.

[4] 冯慈璋. 电磁场[M]. 北京:人民教育出版社, 1979:127-130.

A Calculation Method for the Ferromagnetic Near-field Based on Magnetic Dipole Model

Yu Jie, Lin Chunsheng, Zhou Jianjun
(Department of Weapon Engineering, Naval University of Engineering, Wuhan 430033, China)

In order to calculate the induced magnetic field, a calculation method of the micro magnetic dipole model is studied based on the ordinary magnetic dipole model. The exact expression of the magnetic values at any point in the space is derived. The problems of common magnetic dipole model which can not accurately calculate the near-field source magnetic field values are solved. By calculating the induced magnetic field by the ordinary magnetic dipole model and the micro magnetic dipole model for cylindrical ferromagnet, the results show that the micro magnetic dipole model is of high accuracy, which can be applied to practical engineering.

induced magnetic field; magnetic dipole model; micro; cylindrical ferromagnet

TM936.1

A

1003-4862（2014）03-0012-03

2013-08-15

余杰（1989-），男，硕士研究生。研究方向：目标磁场特性及信号处理 。