基于系统迭代法的线源瞬变电磁近区正演模拟

赖刘保，席振铢,*，王 鹤，侯海涛，朱伟国，刘愿愿，蒋 欢

(1. 中南大学 海洋矿产探测技术与装备研究所，地球科学与信息物理学院，长沙 410083；2. 中南大学 地球科学与信息物理学院，长沙 410083; 3．长沙五维地科勘察技术有限责任公司，长沙 410205)

0 引言

瞬变电磁法(TEM)已广泛应用于矿产资源调绘、水资源调查、地热勘探[1]、岩溶探测以及油气田勘查等领域[2]，国内、外几十年的实践工作说明了该方法在生产实践中应用的有效性[3]。

根据TEM的场源性质，大体分为磁性源和电性源两大类。一般来说磁性源的探测深度在1 km左右，不能满足1 km～3 km的资源勘查、地热探测、区域深部工程地质构造等方面的需求。目前，电性源瞬变电磁主要在远区观测，即长偏移距工作方式(LOTEM)，其采用1 km到3 km的接地长导线发射电磁场，在偏移距3 km～10 km主要观测水平电场分量与垂直磁场分量[4]。前苏联及欧美国家广泛将LOTEM应用于地热勘探、地壳构造调查及地震勘探方法勘查时效果不好的地区，并形成了一套较完整的系统，但是在远区观测时存在信号强度弱、体积效应大等问题，而在近区线源观测则有以下优点：①信噪比高、体积效应小、探测灵敏度高；②电压衰减速度慢，发送磁矩大，探测深度相对较大，装置轻便，适合山区作业等优点[5]。

当前线源近区的研究多局限于二维数值模拟[6]，一维反演解释[7]。随着计算机技术的发展，瞬变电磁的三维正演快速计算模拟可以实现。与需要全空间离散的有限元[8]、有限差分[9-10]所不同的是：积分方程法只需对异常体进行离散，具有离散数目少，求解精度高等优点[11-12]。与较成熟的LOTEM相比，国内、外学者对于线源近区三维正演研究相对较少。主要问题在于三维计算中消耗计算机大量内存和时间，尤其在求解大型稀疏矩阵时，系数矩阵的条件数很大，很难获得高精度的结果[13]。同时在近场区，线源不能采用电偶极子近似[14]，场源剖分时也增加了计算量。为了同时解决三维计算的速度和精度问题，作者引入了系统迭代法求解积分方程来降低系数矩阵条件数，节省计算机的内存及计算时间。

作者首先介绍了层状介质中三维电性异常体的积分方程，给出了第二类Fredholm方程，重点阐述了系统迭代法的求解过程，然后利用数字滤波法将频率域响应转换到时间域；最后在均匀半空间中将正演结果与解析解对比，检验算法的有效性，并结合简单模型与复杂模型的计算，证明了该方法对异常体探测的可靠性。

1 基本理论

1.1 积分方程法

三维模型如图1所示，水平层状电导率的张量形式：σb=diag(σb,σb,σb)，其中σb= σb′ +iωεb为大地的复电导率。层状大地与异常体的电导率之差σ=σaI-σb，其中I为3×3的单位矩阵，σa为异常体电导率，则三维异常体的散射电流为Js=σ·E，E为异常体中的电场强度。假设入射场在时谐因子eiwt，外加电流激励下垂直向下传播，且忽略位移电流。根据MAXWELL方程及相应的电磁格林张量理论，异常体V满足第二类Fredholm积分方程：

(1)

其中θ=diag(1/σa-σb,1/σa-σb,1/σa-σb)；Ep为一次电场；GE=-iwμ0A+(1/σb)▽▽·A为电场格林函数[15]。

将异常体区域V剖分为M个小单元，得到如下矩阵方程：

[Γ][Js]=[Ep]

(2)

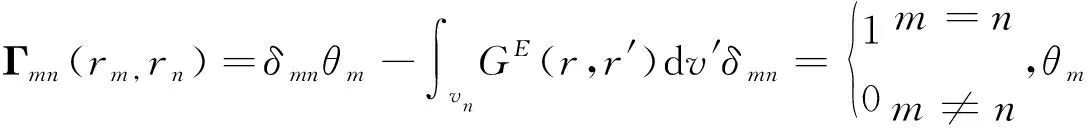
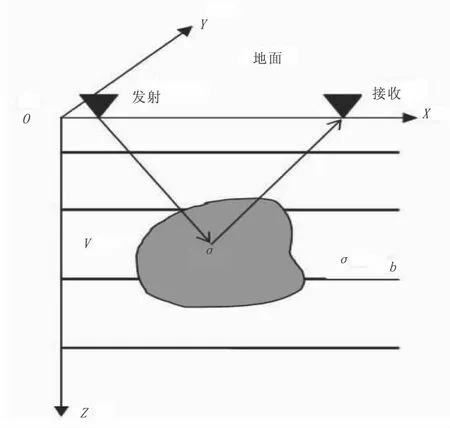
图1 三维地电模型示意图Fig．1 Sketch of 3D geoelectric model

1.2 线源的处理

由于观测点常常比较靠近接地导线源，需把发射源看做多个偶极的叠加，计算电磁场分量时将偶极场表达式沿线源积分，文献[14]给出了层状大地表面的电磁场表达式。假设导线源的中心位于原点，沿水平轴向两侧延伸至-L和L。

水平电场公式为：

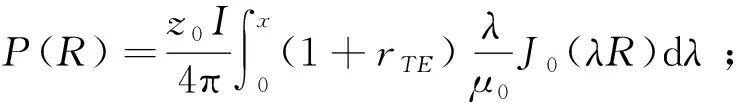
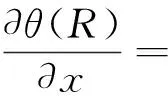
R=[(x-x′)2+y2]1/2;

R1=[(x+L)2+y2]1/2;

R2=[(x-L)2+y2]1/2。

垂直磁场公式为：

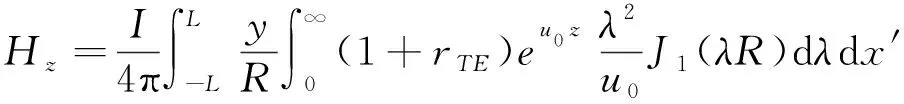
1.3 系统迭代法解矩阵方程

如果把三维异常体V分成m块，V1、…、Vi、…、Vm，然后再将第i块异常体Vi剖分为Mi个小单元，式(1)变为：

(3)

式(3)表明，Vi区域外的异常体对Vi的影响相当于外加激发源的作用。

若把整个异常体区域看成一个系统，则每个块状异常体在各自区域内形成子系统。我们可以单独的处理各个异常体，获得子系统间的相互影响，从而得到整个系统的值，这就是系统迭代法。该方法只需要保存处于计算中的单个异常体的离散单元，而不需要存储整个异常体的全部离散，可以节省时间，节约内存，而且随着剖分越来越细，系数矩阵的条件数越来越大，线性方程组的解越来越不稳定。系统迭代法只跟剖分后异常体的个数有关，而与未知数无关，这样大大降低了矩阵的条件数，提高了精度。

根据矩阵理论，式(3)相当于将散射矩阵Γ离散成块矩阵,式(2)变为：

(4)

用高斯-赛德尔(GS)迭代法求解式(4)：

(5)

为提高收敛速度采用逐次超松弛(SOR)迭代法，式(5)变为：

(6)

其中ω为松弛因子且1≤ω<2。当w=1时，SOR法为GS法，即式(6)等于式(5)。

选择合适的松弛因子可以保证SOR的收敛。经过多次验算，本文w=1.25。

Γii可以通过LU或者Cholesky分解并将离散矩阵用于迭代，Ep可以用快速汉克尔变换计算，异常体部分可以用文献[15]所提到的格林函数法求解。如果迭代的相对误差小于ε，则矩阵方程收敛，迭代终止。

求得Js后，根据并矢格林函数，二次电磁场分别为：

1.4 时频转换

在频率域中求得电磁响应后，利用安德森的滞后褶积的快速数字滤波法[16]计算如下正弦与余弦变换。

Im[E(ω)]和Im[H(ω)]分别是频率域中电、磁场分量的虚部。求得磁场强度对时间的导数∂H(t)/∂t后，再乘真空磁导率μ0=4π×10-7Wb/(A·m)， 可得磁感应强度对时间的导数 ∂B(t)/∂t。

2 算法检验

为了检验本算法的正确性，本研究采用线源赤道轴线上的解析式与积分方程法得到的数值解对比。线源赤道平面如图2。

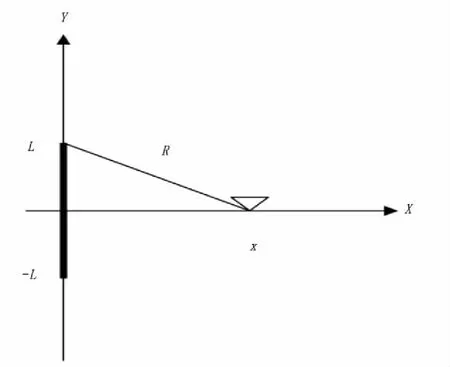
图2 线源赤道平面图Fig．2 Plan view of the line source

假设均匀半空间的电阻率为100 Ω·m,线源长1 km，激发电流1 A,偏移距1 000 m处接收。积分方程计算中，在频率域范围0.01 Hz～1 000 000 Hz中计算了49个频点，每个数量级取6个频点，向时间域0.01 ms～1 000 ms转换中，共计算了31个三维体的瞬态响应，从而保证了计算精度。

从图3中可以看出，不管垂直感应磁场时间倒数还是水平电场强度的衰减曲线结果，都与解析解十分吻合。这也验证本文的数值模拟精度高，计算可靠。

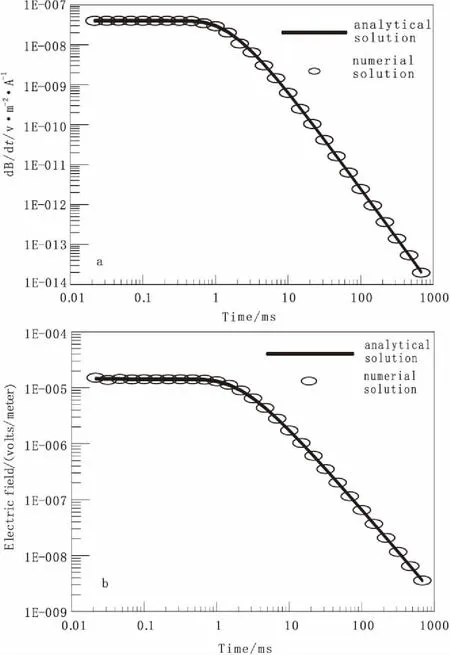
图3 半空间中的解析解与数值解的对比Fig．3 Contrast between numeric solution and analytic solution in a half-space(a) dBz/dt衰减曲线; (b)水平电场Ey衰减曲线

3 模型计算

为了说明线源对异常体的反应效果，分别设计简单模型和复杂模型对瞬态电磁响应加以分析。计算区域示意图4显示：场源(箭头)中心位于原点，长1 000 m；异常体位于5 000 m×4 000 m的地面下，埋深750 m；发送电流1 A，三角形为测点。两个模型的以上参数相同，分别计算垂直感应时间导数与平行于场源方向的水平电场Ey，然后作出等值线图与随时间的衰减曲线图。

图4 三维异常体的平面图和断面图位置A、B、C、D分别对应于偏移距r=-250 m、250 m、1 500 m、3 000 mFig．4 Plan view and cross-section for 3D conductive prism(a)X-Y平面图; (b)X-Z断面图

3.1 低阻模型

图5是一个低阻异常体存在于均匀半空间中的模型。半空间的电阻率为50 Ω·m，异常体电阻率为5 Ω·m，尺寸1 000 m×1 000 m×500 m。将异常体剖分为10×10×10个网格单元。

图5 半空间中的单个三维异常体模型Fig．5 Model of a single anomalous 3-D body in a half-space

图7表示垂直感应磁场的时间导数在不同观测点随时间的衰减曲线。在x=-250 m 处，前支出现反向电流，瞬态值为负，在120 ms方向发生逆转变为正值；x=250 m 刚好相反，只是在80 ms 时刻方向发生偏转，因为B点离异常体更近。这个符号变化特征可以为纵向上确定异常体提供参考[19]，经计算，在80 ms磁场电流扩散到异常体。观测点在横纵向上离异常体750 m左右，而偏移距只有250 m。这表明近区也能探测较远的异常体，随着偏移距的增加，曲线形态逐渐平缓，这点和文献[20]给出的一维计算结果相同。在x=1 500 m、3 000 m时，如同磁性源及LOTEM，感应磁场时间导数随时间按t-5/2衰减，这说明了本文方法的可靠性。

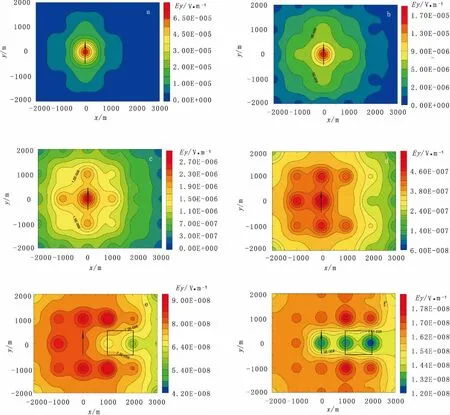
图6 不同时间的水平电场Ey(V/m)等值线Fig．6 Contour maps of horizontal electrical field Ey at different times(a)t=1 ms；(b)t=3 ms；(c)t=10 ms；(d)t=30 ms；(e)t=100 ms；(f)t=300 ms；箭头表示场源，长方形表示异常体的平面位置

图7 不同偏移距的dBz/dt曲线Fig．7 Curves with different offset

3.2 复杂模型

假设电阻率为50 Ω·m 的均匀半空间中分别赋存高、低阻两个异常体：高阻电阻值为500 Ω·m，尺寸1 000 m×1 000 m×500 m,中心点位于(1 500,-1 000,750)；低阻值为5 Ω·m，尺寸1 000 m×1 000 m×500 m，中心位于(1 500,1 000,750)。在计算中将两个异常体各剖分为10×10×10个网格单元，共 2 000个网格(图8)。

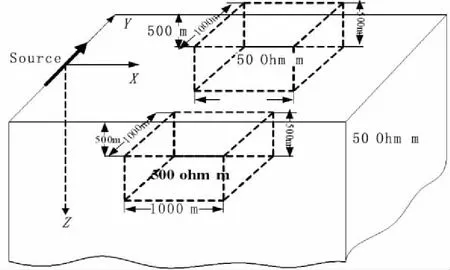
图8 高阻和低阻两个异常体的三维模型Fig．8 Schematic drawing of 3D model with two anomalies in homogeneous half space

水平电场切片图9表明：刚开始，电流主要集中在发射源附近，这点和低阻模型相同，也符合电磁波的传播规律；在100 ms时，在异常体位置正上方出现高、低电场值，如图中矩形所示；当t=300 ms时，异常体的位置反应得更加明显，而且不随时间变化。与图6(f)类似，图9(f)的两个极值对应异常体边界，而且高阻异常体对应高电场值，低阻异常体对应低电场值。因此电场值不仅能反应低阻的存在，而且对高阻体也有较高的分辨率，这是其他装置所不具备的优势在图10中，在低阻模型的同一深度的加入高阻体后，感应磁场时间导数的衰减曲线和单个低阻体的曲线基本相同，随偏移距增加，曲线仍然变缓，只是在x=250 m、t=100 ms瞬态方向发生逆转，比后者晚了20 ms。

以上数值计算是在双核2.4GHz，内存2.0 G的个人笔记本电脑上实现的，在精度达到0.000 1的情况下，低阻模型只需8 min，高低阻模型只需25 min。如果剖分网格单元变小，需要的时间更少，说明系统迭代法能节省时间。

4 结论

本次研究采用基于系统迭代的积分方程法计算了线源近区三维瞬变场值。通过与解析解的对比及两个算例的模拟，得出如下结论：

(1)系统迭代法求解积分方程，不仅节省了内存和计算时间，而且降低了离散矩阵的条件数，提高了计算精度。

(2)水平电场不仅对低阻体有良好的分辨力，而且对高阻也反应灵敏。低阻异常体对应低场值，高阻体对应高场值，同时其极值对应异常体的左右边界，这为今后更好利用电场分量提供了理论基础。

(3)异常体的感应磁场对时间导数的方向发生逆转，而且随偏移距的增加，曲线形态变缓。

图9 高低阻模型不同时间水平电场Ey(V/m)等值线图Fig．9 Contour maps of horizontal electrical field Ey at different times(a)t=1 ms；(b)t=3 ms；(c)t=10 ms；(d)t=30 ms；(e)t=100 ms；(f)t=300 ms箭头表示场源，长方形表示异常体的平面位置

参考文献：

[1] 李文尧，廖忠.瞬变电磁法在腾冲寻找地热中的应用[J].物探与化探，2002，26(5):368-371.

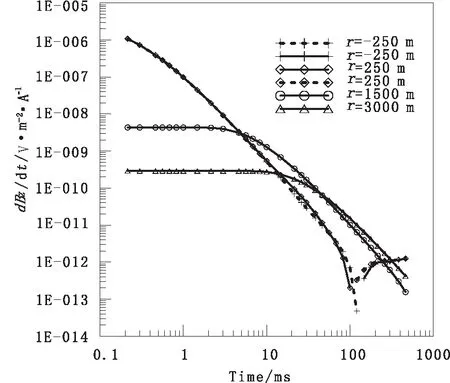
图10 不同偏移距的dBz/dt曲线Fig．10 Curves with different offset

[2] 牛之琏.时间域电磁法原理[M].长沙：中南大学出版社，2007.

[3] 李貅.瞬变电磁测深的理论与应用[M]．西安：陕西科学技术出版社，2002.

[4] 陈明生.电偶源瞬变电磁测深研究(二)[J].煤田地质与勘探，1999，27(2)：54-57.

[5] 赵福元，严良俊，何展翔，等.线源时间域电测深全期全区视电阻率求解[J].地震地质，2010,32(3):473-481.

[6] 严良俊，徐世浙，陈小斌，等.线源二维瞬变电磁场的正演计算新方法[J].煤田地质与勘探，2004,32(5)：58-61.

[7] 刘瑞德，梅岩辉，黄力军.电性源瞬变电磁快速反演解释方法[J].工程地球物理学报，2005,2(1):18-21.

[8] 徐志锋，吴小平.可控源电磁三维频率域有限元模拟[J].地球物理学报，2010,53(8)：1931-1939.

[9] YUTAKA SASAKI, SEONG-JUN CHO.3D finite-difference modeling of time-domain electromagnetic data for mineral exploration[C].Proceedings of the 10th SEGJ Interational Symposium,2011:235-238.

[10] TSILI WANG, ALAN C TRIPP,Gerald W HOHMANN. Studying the TEM response of a 3-D conductor at a geologucal contact using the FDTD method[J].Geophysics,1995,60(4):1265-1269.

[11] GERALD W,HOHMANN.Three dimensio-nal em modeling[J].Geophysical Surveys,1983,6(1983):27-53.

[12] PHILIPE,WANNAMAKER,GERALDW.Hohmannand Willian A.SanFilipo.Electromagnetic modeling of three-dimensional bodies in layered earths using integral equations[J].Geophysics,1984,49(1):60-74.

[13] ZONGHOU XIONG.Electromagnetic modeling of 3-D structures by the method of system iteration using integral equations[J].Geophysics,1992,57(12):1556-1561.

[14] 米萨克 N.纳比吉安.勘察地球物理电磁法 第一卷:理论[M] .赵经祥，王艳君译.北京：地质出版社，1992.

[15] ZONGHOU XIONG. Electromagnetic fields of electric dipoles embedded in a stratified anisotropic earth[J]. Geophysics,1989,54(12):1643-1646.

[16] WALTER L,ANDERSON. Fast Hankel transforms using realted and lagged convolutions[C]. ACM Transactions on Mathematical Software,1982,8(4):344-368.

[17] ORISTA GLIO ML..Diffusion of electromagnetic fields into the earth from a line source of current[J].Geophysics,1982,47(11):1585-1592.

[18] NABIGHIAN M N, ORISTAGLIO M L On the approximation of finite loop sources by two-dimensional line source[J].Geophysics,1984,49(7):1027-1029.

[19] BRIANM.GUNDERSION,GREGORY A.NEWMAN,Gerald W.HOHMANN. Three-dimensional transient electromagnetic response for a grounded source[J].Geophysics,1986,51(11):2117-2130.

[20] 薛国强，陈卫营，周楠楠，等.接地源瞬变电磁短偏移距深部探测技术[J].地球物理学报，2013,56(1)：255-261.