基于模式识别理论基坑监测数据周期性误差分析

田劲松 ，田文峰

(1.安徽农业大学 理学院，安徽 合肥 230036; 2.黄山市黟县宏村镇人民政府，安徽 黄山 245500)

1 引 言

工程基坑开挖过程中，在重复测量时间间隔较短且连续变形测量时，测量数据常包含由各种因素(例如:仪器、外界环境等)引起的误差。因此，在变形分析前必须对所获数据进行识别，以确定该批测量数据是否受周期性误差的干扰。要识别测量数据的周期性误差，传统解决方法是利用数理统计中的统计检验方法。但是，统计检验方法在结论的可靠性方面，存在着诸多缺点，致使结论的正确性可疑。国内许多学者力求在该方面从方法和手段上得以突破，并且做了不少工作。探讨利用模式识别理论的思想和方法解决识别测量数据周期性误差问题，无论是统计检验还是模式识别最终解决的都是测量数据有没有周期误差的问题。将基坑监测数据确定为含周期性误差类和不含周期性误差类。统计检验法的分类方法是在一定显著水平的情况下确定类别，模式识别分类法是基于贝叶斯风险函数最小为基本思想来确定类别的，其结果的误判概率总是最小且可以给出分类判别结果错误率，具有很大的优点［1］。本文利用模式识别的思想和方法分析基坑土体倾斜监测数据是否含有周期性误差问题。

2 模式识别方法

模式识别方法主要有决策理论方法和句法方法。决策理论方法又称为统计方法，是发展较早也比较成熟的一种方法。把识别对象变换为适于计算机处理的数字信息。在数字化环节之后进行预处理，除去混入的干扰信息并减少某些变形和失真。随后进行特征抽取，即从数字化后或预处理后的输入模式中抽取一组特征。所谓特征是选定的一种度量，它对于一般的变形和失真保持不变或几乎不变，并且只含尽可能少的冗余信息。特征抽取过程将输入模式从对象空间映射到特征空间。这时，模式可用特征空间中的一个点或一个特征矢量表示。这种映射不仅压缩了信息量，而且易于分类。在决策理论方法中，特征抽取占有重要的地位，通过分析具体识别对象决定选取何种特征。特征抽取后进行分类，即从特征空间再映射到决策空间。为此而引入鉴别函数，由特征矢量计算出相应于各类别的鉴别函数值，通过鉴别函数值的比较实行分类。

3 周期性误差模式识别模型

依据《建筑变形测量规程》(JGJ/T83 －2007)、《建筑基坑工程监测技术规范》(GB 50497 －2009)、《工程测量规范》(GB 50026 －2007)，基坑监测主要含有水平位移监测、土体沉降监测、深层土体测斜监测和地下水位监测、周围建筑物沉降监测等［2］，不管哪种类型的监测，都是在一定周期内对监测对象进行重复测量。

3.1 数据特征选取

根据技术设计要求，测量间隔是一天或几天。设重复测量的数据是等时间间隔，每个监测点的观测周期为n，周期序号为m，将观测数据组成如下矩阵形式:

如果观测数据存在周期性误差，观测数据矩阵中同列内部各测量数据差别很小，但不同列测量数据之间差别较大;如果观测数据不存在周期性误差，各测量数据之间的差别主要由偶然误差因素引起。利用统计方法中的方差分析法进行特征选取，即计算各列之间数据平方和W外与同列内平方和W内，由列间平方和W外与列内平方和W内分别作统计分析，得到统计量S内和S外，在误判概率很小的情况下，利用模式识别的分类方法，如果能将S内和S外分为两类，说明数据矩阵中存在周期性误差的影响。列间平方和W外与列内平方和W内统计计算公式分别为:

由列间平方和W外与列内平方和W内分别作统计分析，得到统计量S内和S外分别为:

3.2 模式识别

一系列基坑观测数据，并不知道是否受到周期性误差的影响，但不管怎样的结果，都只有两种情况:一是仅受偶然误差的影响(规范允许)，二是虽然含偶然误差但周期性误差的影响较明显(规范不允许)，把第一种情况称为Ⅰ类模式，第二种情况称为Ⅱ类模式。如果经模式识别后，在一定可靠性的基础上能将S内和S外分开，则该系列观测数据含周期性误差且影响较明显，属于Ⅱ类模式，否则，属于Ⅰ类模式，要得到以上的结果，必须确定模式识别分类准则函数［3，4］。

(1)分类准则函数

分类准则函数反映模式类别的可分性和衡量分类方法对分类的有效性。参考选取散度JD准则，因为散度JD准则是基于贝叶斯决策理论的最大似然化判决规则，反映模式类别的可分性，散度JD的计算模型为［3，4］:

式中，P(x/ωi)、P(x/ωj)为两类ωiωj的类概率密度;Ed为x 的值域空间;x 为特征变量，即为S内或者S外向量。

讨论基坑监测数据，不管是沉降(高程)、水平位移(偏移量)等都是一维问题且特征变量为χ2分布，在自由度较大时可以近似看成正态分布，所以，将散度JD的计算模型转化为［3，4］:

正态分布时:

两类的协方差矩阵相等时:

式中，μi、μj为两类模式的均值矩阵。

根据具体的实测数据确定散度JD的基准θD，基准θD的计算模型为:

式中，JD为散度，α 为F 检验的置信度，一般情况下α=95%。如果，则说明S内和S外可分，识别结果为该系列观测数据含周期性误差且影响较明显，属于Ⅱ类模式;如果，则说明S内和S外不可分，识别结果为该系列观测数据不含周期性误差，属于Ⅰ类模式。

(2)识别结果的错误率

无论采用哪种分类方法，识别结果都存在误判的情况，在利用模式识别方法对基坑监测数据进行识别和判断后，识别结果的可靠性判断也是非常重要的问题。识别结果的错误率可以近似采用如下模型进行解析计算［3，4］:

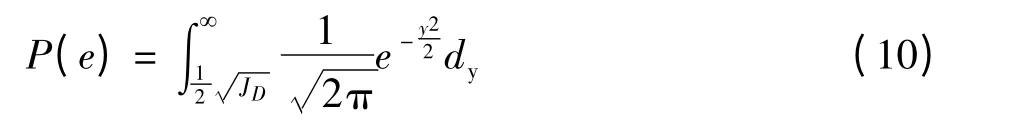
式中，JD为该条件下的散度准则。

4 实例分析

4.1 工程概况

该工程位于安徽省淮北市黎苑路以北，南湖路以东，为矿务局机关宿舍，均为7 栋Ⅰ类高层住宅。根据地质勘察报告，土质为粉质粘土;地下水位稳定在31.0 m，场地自然地面标高在32.5 m ～33.8 m之间(平均33.15 m)。基坑土方最深需下挖8.9 m，施工期间，通常应降水至基底0.5 m ～1.0 m，降水后水位标高23.25 m，降水深度7.75 m。基坑周边设置20 个基坑沉降监测点(编号为CJ01 －CJ20)，20 个土体水平位移监测点(编号为SP01 －SP20)，15 个深层土体位移监测点(编号为CX01 － CX15)，埋管深度为7.5 m，监测点设置如图1所示。

图1 测斜监测点布置图

4.2 深层土体位移监测数据

基坑监测项目较多，包含支护结构的沉降监测、土体水平位移监测、深层土体倾斜监测、周围建筑沉降监测等［5，6］，选取编号为CX01 深层土体位移监测点的测斜数据为例进行分析，利用模式识别模型，判断测量数据是否含有周期性误差，取置信度为95%，CX01 监测点观测数据如表1所示，CX01 监测点的本期倾斜量和累计倾斜量见图2所示。分别采用模式识别方法和F统计检验方法对观测数据进行分析。

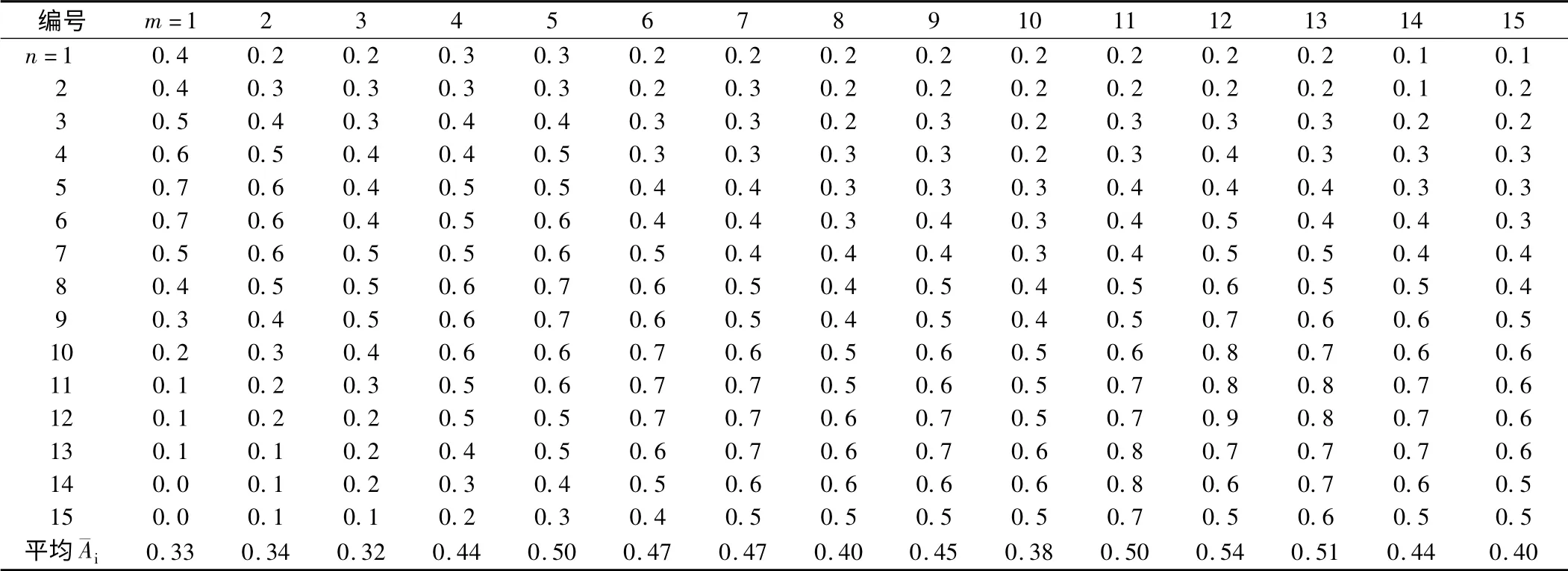
表1 土体倾斜观测数据

图2 位移曲线图

4.3 模式识别分析

(1)确定特征变量S内和S外:观测数据组成如下矩阵后，行n=15，列m=15。

列内自由度为［m(n －1)］=182，列间自由度(m－1)=14，所以特征变量(子样方差)S内和S外则为:

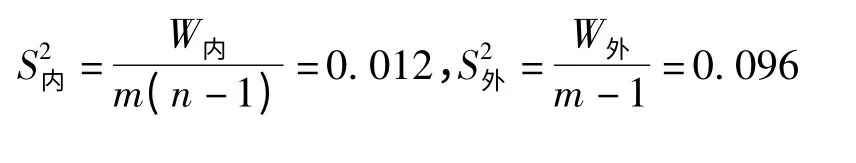
(2)散度准则JD及可靠性

计算时，母体均值和方差用子样均值和方差来代替，则散度准则JD为:

散度JD的基准

在mathematica 软件中计算得到:

(3)模式识别结论

4.4 F 统计检验分析

用F 检验法对同批土体倾斜监测数据进行检验，统计分析检验分析是否含周期性误差。子样方差分别为:，方差小于，所以计算得到F 值为:分别服从于自由度为［m(n －1)］=182 和(m －1)=14 的χ2分布，置信度为95%，经查表，F0.05=1.0。F ＞F0．05，说明数据存在显著性差异，判断这批数据受周期性误差影响显著，与模式识别的结论一致。

5 结 论

(1)模式识别的思想和方法可以解决判断同一对象重复多次观测后是否受周期性误差的影响。

(2)模式识别分类法是基于贝叶斯风险函数最小为基本思想来确定类别的，其结果的误判概率总是最小且可以准确给出分类判别结果错误率。

(3)统计检验方法与模式识别方法解决此类问题的最大区别在于判别结论的可靠性方面。统计检验方法是在一定显著水平的基础上确定类别和计算的，是统计学上的结论，可靠程度存疑。模式识别方法依靠一定的数学模型，得到判识结果的错误率。文中案例，借助模式识别方法，判断这批土体倾斜观测数据受周期性误差的影响显著，且模式识别结果的错误率为0.0006。

(4)基坑水平位移监测数据存在周期性误差主要是由外界因素造成的，比如天气、温度、基坑开挖进度、基坑周边的地下水等对测量数据产生周期性的干扰。对存在周期性误差的监测数据，具体应用时对数据进行判识和分析，消除误差的影响。

［1］独知行，靳奉祥，赵君毅．工程变形监测模型与方法［M］．北京:测绘出版社，2009．

［2］GB50497 －2009．建筑基坑工程监测技术规范［S］．

［3］独知行，靳奉祥．重复测量周期性误差的模式识别方法［J］．四川测绘，1999，22(1):11 ～13．

［4］独知行，靳奉祥，王同孝．基于散度J_D 准则的位移量显著性模式识别方法［J］．勘察科学技术，1998(6)，43 ～47．

［5］李明峰，蒋辉．基坑支护结构变形监测数据的联合处理［J］．测绘通报，2003(9):48 ～55．

［6］李明峰，陈国兴，安庆军．顾及模型误差的基坑位移监测数据处理方法［J］．防灾减灾工程学报，2005，25(4):468 ～470．

［7］于中伟，花向红，张伟等．厦门机场路深基坑工程变形监测与数据分析［J］．测绘信息与工程，2008，33(5):22 ～24．

［8］独知行，靳奉祥，王同孝．测绘模式识别研究的几个问题［J］．东北测绘，1998，21(2):3 ～4．