数据转换中弧线失真问题的研究

魏金占 ，唐媛

(1.南宁市勘察测绘地理信息院，广西 南宁 5300221; 2.南宁市房产信息管理服务中心，广西 南宁 530022)

1 问题由来

当前存在多种CAD 平台和GIS 平台，数据交换和共享十分频繁，但由于其数据结构不尽相同，数据模型理解的差异等原因，造成数据交换共享时部分信息的丢失，特别是对于曲线元素如常见的弧线，数据的失真特别严重。通常通过数据转换，会有三种失真，一种是完全用特征点拟合的方法，数据失真最为严重，如弧段在转换后就用三个特征点来描述，如图1所示。

图1 特征点拟合弧线转换前后对比

另一种失真较小，它也用多点拟合来描述对象，如图2所示:

图2 多点拟合弧线转换前后对比

还有一种失真度最小，它也用弧线来描述对象，但是因为数据模型理解差异等原因，也存在细微的差异，如起始点结束点微小偏移等，如图3所示。

那么通过原有的思路数据转换时存在差异，能否从概念上更新原有的思路，用一种新的方式来尝试解决问题?下文将结合实例阐述一种新的弧线转换的思路，供大家思考。

图3 失真较小的弧线转换前后对比

2 弧线转换的新思路

弧线的要素通常包括长半轴、短半轴、起始点、结束点和旋转角等，常规方法通常采用如下模式:获得原有图形的几何特征点或关键元素(如角度)，然后通过常规算法，在新的平台下恢复弧线图形，如图4所示。

图4 常规算法弧线的构建

虽然通过此种算法一般可以实现弧线的数据转换，但存在以下问题:DGN 对象中，弧线不仅包括常规的圆弧曲线，也包括拉伸旋转常规弧线后的各类椭圆弧曲线，这样对于后者的描述和转换就显得非常复杂。常规思路是研究旋转拉伸的参数，之后再通过复杂算法实现数据的转换，这种方法十分复杂，理解、实现难度大，而且容易出现数据转换失真。

一般弧线的要素通常包括长短半轴、起始点、结束点和旋转角等，弧线的描述通常采用以下概念［1］，如图5所示:

图5 弧线描述示意

但是因平台对数据模型定义不同，如起始角、扫角和旋转角定义的不同，仅仅通过特征数据来直接在新平台下构建新对象，必将造成数据的失真。经研究发现，虽然数据模型不尽相同，但是其几何特征点的位置在转换前后必须要保证一致，因此利用这一特性，重新定义和计算这些角，再用新的方法来构建几何对象，下文将用实例进行详述。

3 实验验证

在数据转换实验中，发现当完全按照传统的方法直接利用DGN 提供的特征数据在SuperMap 中构建对象时，总会出现细微的差异，如图3所示，转换前后起始端会有细微偏差。原因就在于对弧线特征角描述的不同。首先对特征角重新定义:

旋转角指长半轴所在的直线与Y 坐标轴的夹角θ;

起始角指圆心和起始点连线与长半轴的夹角α;

结束角指圆心和结束点连线与长半轴的夹角β。

对于弧线，尝试用以下新的方法求解特征角:首先计算出圆弧的旋转角θ，之后求出圆弧起始点和圆心连线的角度α，圆弧结束点和圆心连线的角度β，则(α－θ)和(β －θ)分别为此弧线的起始角和结束角。通过重新定义设置旋转角、起始角和结束角计算方法，就可以采用新的方法来实现数据的转换了。这种方法与原有弧线描述的差异在于，新的思路撇开原有旋转角、起始角和结束角，重新定义设置这些角的计算方法，其优点在于无论何种平台，其特征点是一致的，通过统一定义和计算旋转角、起始角和结束角，避免各平台对弧线描述的差异如旋转角定义的不同，达到数据的无损转换。各角定义如图6所示:

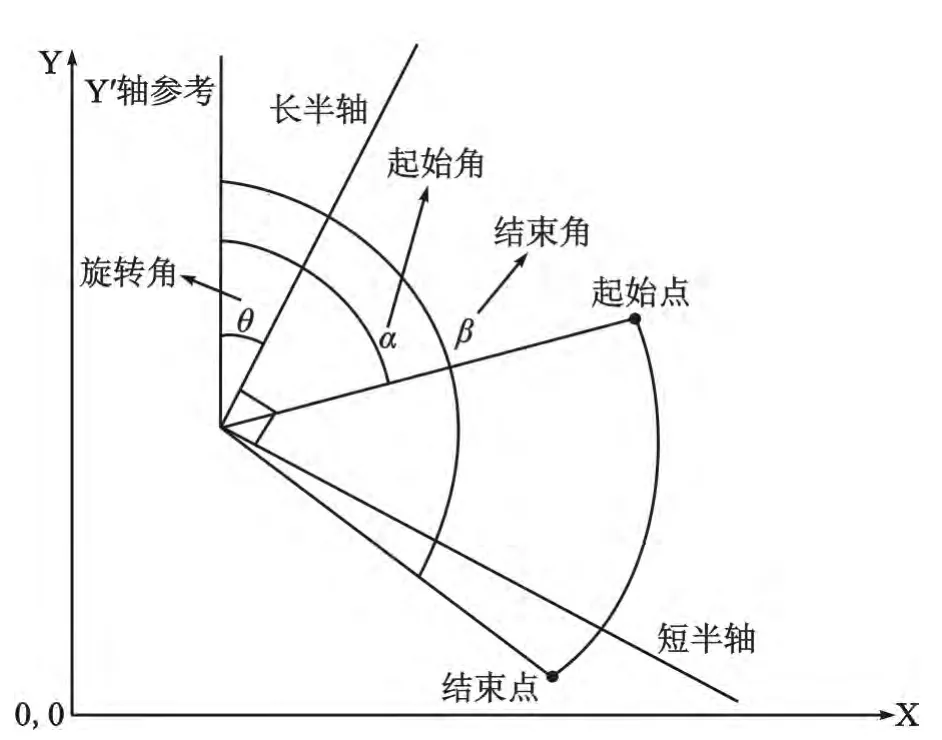
图6 特征角定义示意图

其关键函数代码如下:

是数据转换前后对比如图7所示:

图7 新算法数据转换前后对比

4 结 论

数据转换失真的原因很多，其中对于数据模型理解的差异是关键因素之一。本文针对弧线提出新的转换方法，其思路依然是采用已有的函数重新定义弧线的各个元素，转换的效率与平台自身的转换效率相同。经实验基本上可以消除数据转换的失真问题，对旋转挤压变形的复杂弧线的转换，亦未发现失败情况。与FME 等传统数据转换软件相比，其优势在于直接转入对应的GIS 平台，数据信息损失最小。对于清华山维、超图及ArcGIS 等常见GIS 平台而言，此方法也为类似问题的处理提供新的解决思路。

［1］Bentley Corporation．MicroStation V8 Visual Basic for Applications help［R］．Bentley Corporation，2004．

［2］魏金占，熊旭平，施真娥．MapInfo 中折线分割功能的扩展［J］．信息技术与信息化，2005(1)．

［3］郭功举．面向对象的复杂多边形裁剪实现［J］．现代测绘，2003(8)．

［4］杨光，于野．GIS 与CAD 的特点［J］．东北测绘，1998(1)．

［5］符韶华．DLG 到GIS 数据转换方法研究［D］．阜新:辽宁工程技术大学，2002．

［6］白洪涛，张其林，魏吉东．寻找任意线段和圆弧围成区域的一种算法［J］．计算机应用，2001(10)．