基于等参数线法离散NURBS曲面的插补算法
李学斌
(内江职业技术学院,四川 内江 641100)
1 引言
在模具、航空等制造领域,经常会遇到复杂曲线曲面的数控加工。传统的数控系统往往只具有直线和圆弧插补,对于非直线或圆弧的曲线插补则往往采用微小段直线或圆弧分段逼近的方法,这种方法在处理复杂曲线时会导致诸如数据量大、进给速度不均、精度和通用性较差、编程复杂等问题。目前只有极少数FANUC、SIEMENS、三菱等高档计算机数控CNC(Compute Numerical Control)系统装备有非均匀有理B 样条NURBS(Non Uniform Rational B-Spline)曲线插补功能[1]。随着曲面造型的复杂化,传统的曲面加工方法(如环切法、螺旋线法[2]等)已无法满足提高加工效率的要求。基于以上原因,一些学者提出了曲面的直接插补SDI(Surface Direct Interpolation)算法,这种插补方法极大地提高了插补精度和插补速度。本文介绍一种基于等参数线法离散NURBS 曲面的插补算法,该算法通过离散NURBS 曲面获得一族NURBS 曲线,最后按NURBS 曲线直接插补算法来进行插补。
2 NURBS 曲线曲面定义
2.1 NURBS 曲线定义
根据德布尔(deBoor)和考克斯(Cox)导出的B样条递推定义,B 样条曲线定义为:

式中:Ci(i=0,1,…n)为控制顶点,又称德布尔点,Ni,p(u)称为p 次规范B 样条基函数,双脚下标中的i 表示序号、p 表示次数。由德布尔—考克斯的递推公式定义:

式中:ui称为节点,当ui+1-ui=常数时,则表示均匀B样条函数,反之称为非均匀B样条函数,即NURBS曲线。
NURBS 曲线定义:

式中:Wi是与控制顶点Ci相对应的权因子。
2.2 NURBS 曲面定义
空间曲面的参数方程可表示为:
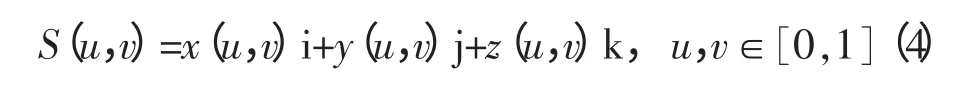
B 样条曲面则定义为:

其中:其中Ci,j(i=0,1,……n;j=0,1,……m)为控制顶点,Ni,p(u)和Nj,q(v)分别是沿u 向节点矢量和υ 向节点矢量定义的p 次和q 次B 样条基函数,u和υ 是曲面的两个参数。
NURBS 曲面定义[3]为:
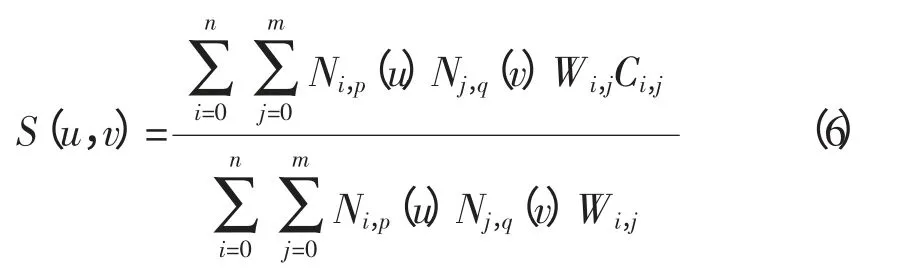
式中:Wi,j是与控制顶点Ci,j相对应的权因子。
在实际应用中,常将节点矢量U 和V 中两端节点重复度取为p+1 和q+1 个,并且两端节点值分别为0 和1,即表示为:

根据上述定义可知,NURBS 曲面就由基函数的幂次、控制顶点、节点矢量和权因子所确定。
3 NURBS 曲面插补技术
3.1 NURBS 曲面插补思路与方法
对于NURBS 曲面的插补,可采取先将NURBS曲面离散成NURBS 曲线的方法。将曲面离散成曲线的方法通常有两种:一是平面切割法,就是用一族平行平面切割曲面,获得一系列的NURBS 曲线,然后按NURBS 曲线进行插补;二是等参数线法,就是先将曲面的两个参数u 和υ 中的任意一个进行离散,可获得一系列的参数值,将这些参数值代入曲面公式,获得一系列的NURBS 曲线,最后按NURBS 曲线进行插补。
插补的实质就是点的密化,密化的常用方法有等距法、等步长法和自适应法等。等参数线法就是先将曲面上两个参数中的一个参数进行点的密化,获得该参数上一系列点的参数值,再按曲面规律得到另一参数上一系列对应点的参数值。这种方法的好处是可以将一部分计算放在插补前集中进行计算,当计算出两个参数值之后,就可以求出曲线上相应的型值点了,同时求出该点的一阶、二阶导矢量,既加快了计算速度,又提高了插补的实时性。
3.2 等参数线法离散曲面法则
为讨论方便,假设先u 向、后υ 向进行。
(1)取参数υ 为某一定值,可得到一条等参数曲线。如令υ=υe,NURBS 曲面就被离散成等参数值为υe的一条NURBS 曲线,记为S(u,υe),如图1所示。

图1 等参数线法离散NURBS 曲面示意图
(2)确定加工行距(即υ 向的进给距离,也是υ向的增量Δυ)时要保证残留高度在规定误差范围之内。
(3)取边界曲线S(u,0)和S(u,1)分别作为NURBS 曲线插补的起始边界和终止边界。
4 NURBS 曲线插补算法
4.1 预处理中的一阶二阶导矢计算
在插补前的预处理中,主要要完成NURBS 曲线在某一点处一阶、二阶导矢的计算任务,即对上述(3)式求一阶、二阶导数,其目的是为获得该点处的一阶、二阶导矢量,为实时插补作好数据准备。
对(3)式进行一阶求导得:

由此得到X、Y、Z 方向的一阶导矢计算式:

式中:xi=Px(ui),yi=Py(ui),zi=Pz(ui)。
由(9)式就可求出NURBS 曲线上ui点处的一阶导矢量[x′(ui),y′(ui),z′(ui)]。
同理对(8)式再次求导可获得NURBS曲线上ui点处的二阶导矢量[x″(ui),y″(ui),z″(ui)]。
4.2 进给速度计算的预处理
为了保证加工精度,必须将弓高误差控制在允许的范围内,因此进给速度应根据曲线曲率半径的变化自动地进行调整,可以采用圆弧逼近的近似处理方法来确定,如图2所示。

图2 圆弧逼近法近似计算进给速度
图2表示的是用一段圆弧在区间u∈[ui,ui+1]内近似地代替NURBS 曲线。C(ui),C(ui+1)分别为近似圆弧上ui点和ui+1点的插补点,P(ui)、P(ui+1)分别为NURBS 曲线上ui点和ui+1点的插补点。
弓高误差ERi、曲率半径ρi、NURBS 曲线上ui点处切线方向的进给速度V(ui)和插补周期T 的关系式如下:

式中:ρi是曲率ki的倒数,ki可按式(11)计算。

假设编程进给速度为F,允许的最大弓高误差为ER,由于在实际加工中,插补周期T 非常小,进给步长ΔLi也非常小,可认为与该段弧长相等,因此V(ui)可近似认为与编程进给速度F 相等。为使弓高误差ERi≤ER,需自动调节进给速度V(ui)的大小,调整规律[4]如下:
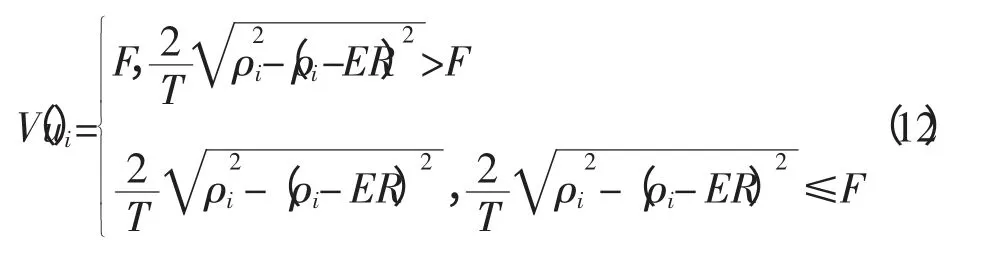
4.3 曲线插补算法
插补过程就是插补点的密化过程,也就是在一个插补周期内,根据上述求出的一阶、二阶导矢量和确定的进给速度V(ui),利用当前的参数值ui实时地计算出下个周期的参数值ui+1,再求出曲线上插补点Pi+1坐标值的过程。
曲线参数u 是时间t 的函数,记为u(ti)=ui,u(ti+1)=ui+1,将参数u 对时间t 进行泰勒展开可获得相应的近似计算。
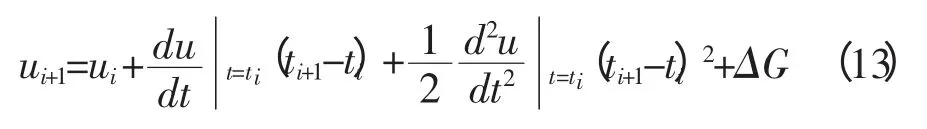
式中:ti+1-ti=T,T 称为插补周期,ΔG 为高阶微量。
一阶泰勒展开的近似表达式为:

二阶泰勒展开的近似表达式为:

将(16)式代入(14)式可得到求ui+1的一阶近似表达式:

如果想得到更高的加工精度,减小进给速度的波动,可根据(15)式求ui+1的二阶近似表达式:

将(17)式或(18)式求出的参数值ui+1代入NURBS曲线方程就可获得下一个插补点Pi+1或该插补点的坐标值,即:

以上就是根据泰勒展开法求解NURBS 曲线的一阶或二阶的插补算法过程。
5 误差分析
在实时插补过程中,因为每求出一个ui+1后都是代入NURBS 曲线方程求出该插补点的x、y、z坐标值,因此插补点必然是在NURBS 曲线上,不存在插补点偏离曲线的误差。误差主要来源存在于进给速度V(步长ΔLi的大小)和弓高误差ERi上。由于在插补前的预处理中已作了根据弓高误差自动调整进给速度的计算,已把误差控制在允许的范围内,所以这种插补方法足以满足精度要求。
6 结束语
本文详细讨论了将NURBS 曲面采用等参数线法离散成一族NURBS 曲线,然后按NURBS 曲线的直接插补算法进行的NURBS 曲面插补。在NURBS 曲线的插补算法过程中,根据加工精度要求的高低,采用了泰勒一阶或二阶展开的递推方式求出下一参数值ui+1,从而获得插补点Pi+1的x、y、z 坐标值,整个算法以控制弓高误差在允许范围内并适时调整进给速度为前提,保证了曲面的加工精度。
[1]徐 宏,胡自化,张 平,杨冬香,杨端光.基于冗余误差控制的非均匀有理B 样条曲线插补算法研究[J].计算机集成制造系统,2007,(5).
[2]孟书云,赵东标.复杂曲面笔式加工的直接插补算法[J].东南大学学报,2006,22(1):73-77.
[3]李 霞,梁宏斌,邱长华.基于STEP-NC 的NURBS 曲面插补技术的研究[J].计算机集成制造系统,2008,(6).
[4]梁宏斌,王永章,李 霞.自动调节进给速度的NURBS插补算法的研究与实现[J].计算机集成制造系统,2006,(3).
[5]魏胜利,常国权.NURBS 曲线曲面插补算法基于S12 的测试[J].电脑知识与技术,2010,(9).
[6]孙玉娥,林 浒,盖荣丽.基于速度平滑控制的高效非均匀有理B 样条曲线插补算法[J].计算机集成制造系统,2008,(11).
[7]范克东,肖世德,龚邦明.实现高速高精度加工的智能NURBS 插补算法研究[J].制造业自动化,2006,(4).
[8]徐夏民,邵泽强.数控原理与数控系统[M].北京:北京理工大学出版社,2009.

