离散广义分段仿射系统弹性H∞滤波器的设计

周振华，王 茂，王学翰

（1.哈尔滨工业大学空间控制与惯性技术研究中心，150001哈尔滨；2.大庆油田电力集团燃机电厂，230604黑龙江大庆）

离散广义分段仿射系统弹性H∞滤波器的设计

周振华1，王 茂1，王学翰2

（1.哈尔滨工业大学空间控制与惯性技术研究中心，150001哈尔滨；2.大庆油田电力集团燃机电厂，230604黑龙江大庆）

为消除未知情况下外部干扰和测量噪声对控制系统性能的不利影响，以一类参数不确定性体现为范数有界形式的离散广义分段仿射系统为模型，研究具有H∞性能指标渐近稳定弹性滤波器的设计问题.通过采用广义分段仿射Lyapunov函数、投影定理以及几个基本引理，提出了对于由所设计弹性滤波器构成的滤波误差动态系统满足鲁棒H∞性能指标的反馈控制器设计方法.通过求解一组包含参变量的LMIs，可以得到保证广义分段仿射系统具有H∞性能的反馈控制器增益和渐近稳定弹性滤波器的待定系统矩阵，仿真结果证明了所提设计方法的有效性.

广义分段仿射系统；弹性滤波器；分段Lyapunov函数；LMIs

目前，具有范数有界时变参数不确定性广义分段仿射系统的鲁棒稳定性问题越来越受到人们的关注［1-3］，但关于系统“软测量技术”的研究鲜有报道.这样的系统不但要求具有鲁棒稳定性，同时也需要利用系统的输入输出信息来重构系统的状态向量［4］，这种处理方法的目的在于寻求一个渐近稳定滤波器，使得由此构成的滤波误差动态系统渐进稳定，而且要求系统满足一定的H∞性能指标［5-7］.

随着广义系统鲁棒控制问题研究的深入，对其进行滤波器设计的相关研究也相继取得了一些成果［8-10］，所做研究大多局限于连续系统，采用的方法主要是基于分段Lyapunov函数法以及一些相应线性矩阵不等式的处理方法［11-13］.然而，关于离散广义分段仿射系统H∞滤波器设计方法的研究却未见报道.王茂等［14］研究了一类具有参数不确定离散广义分段仿射系统的静态输出反馈控制问题，将结果转换为包含参变量的LMIs约束条件，得到欲寻求使闭环系统容许的反馈控制器增益.本文基于分段Lyapunov函数，投影定理以及几个基本引理，在前人的基础上引入弹性H∞滤波器设计方法对离散广义分段仿射系统设计一个鲁棒H∞滤波误差动态系统.

本文特点在于将一类参数不确定性体现为范数有界形式的离散广义分段仿射系统的弹性H∞滤波器设计方法进行考虑，以一些线性矩阵处理方法的基本引理为基础，同时采用投影定理对系统的保守性进一步降低，使得由引入此滤波器而构成的滤波误差动态系统满足鲁棒H∞性能指标.

1 问题描述及基础知识

本文考虑的是一类参数不确定性体现为范数有界形式的时变参数广义分段仿射系统：

式中：χ（k）∈Rnχ为系统状态变量；u（k）∈Rnu为控制输入向量；y（k）∈Rny为系统输出向量；z（k）∈Rnz为可控输出向量；w（k）∈Rnw且w（k）∈l2［0，∞）为扰动输入；Ai，Bi，Ci，Di1，Di2，Li，bi，E为第i个子系统的已知定常系数矩阵；Ebi是偏置项；索引集合是I＝｛1，2，…，N｝；E∈Rnχ×nχ是广义矩阵，且rank（E）＝r≤nχ；ΔAi和Δbi代表系统的不确定项，且满足如下形式：

式中：Wi1，Ei1和Ei2是预先指定的定常实数矩阵，Δi（t）：Z＋→Rs1×s2是一个未知的实值时变矩阵函数，并且包含Lebesgue可测量元素，具有如下形式：

如果式（2）和式（3）成立，则称系统具有容许的参数不确定性.

在子系统中，将多面体区域Ri过渡到区域Rj的集合用Ω表示，可以描述为

本文假设多面体区域Ri，i∈I具有形式：

该多面体区域可以进一步描述为一个椭圆集合，其中Fi＝2Ci／（βi-αi），fi＝-（βi＋αi）／（βi-αi），εi＝｛χ｜‖Fiχ＋fi‖≤1｝，i∈I．

对于每个椭圆区域，可以得到：

进一步将状态空间分为两类区域I＝I0∪I1，I0代表包含原点的fTifi-1≤0索引集合区域，I1则代表其余的索引集合区域．

定义1［15］考虑参数不确定体现为范数有界形式的离散广义分段仿射系统（1），其中u（k）＝0．

i.如果存在z∈C使得det（zE-Ai）≠0，则称广义系统（1）是正则的，i∈I；

ii.如果deg（det（zE-Ai））＝rank（E），i∈I则称系统（1）是因果广义系统；

iii.用λ（E，Ai）表示离散广义系统（1）的所有特征根，如果λ（E，Ai）⊂Dint（0，1），则称（1）是稳定的广义系统；

iv.如果称广义系统（1）是容许的，则系统（1）必定正则、因果，而且是稳定的；

v.用ν1表示矩阵束（E，Ai）的一阶向量，且非零向量ν1满足Eν1＝0，对于满足Eνk＝Aivk-1的非零特征向量νk（k≥2），则称为矩阵束（E，Ai）的k阶特征向量．

引理1 对于适当维数实矩阵M＝MT、S、N和Δ（t），若满足ΔT（t）Δ（t）≤I，则当且仅当存在某个标量ε＞0时：M＋SΔ（t）N＋NTΔT（t）ST＜0等价于M＋εSST＋ε-1NTN＜0．

引理2［16］（投影定理）：给定矩阵h＝hT∈Rn×n，u∈Rk×n和v∈Rm×n，则关于变量Δ的矩阵不等式h＋uTΔTv＋vTΔu＜0是LMI可解的，当且仅当：

1）若v⊥＝0，u⊥≠0，则uT⊥hu⊥＜0；

2）若u⊥＝0，v⊥≠0，则vT⊥hv⊥＜0；

3）若u⊥≠0，v⊥≠0，则uT⊥hu⊥＜0，vT⊥hv⊥＜0同时成立，u⊥，v⊥代表u和v的右正交核空间．

引理3［17］若ψ0（ξ），ψ1（ξ），…，ψp（ξ）为ξ∈Rn的二次仿射函数，其中ψi（ξ）＝ξTQiξ，i＝0，1，…，p，且Qi＝QTi．对于一组正数μ1，μ2，…，μp≥0，若对任意ξ∈Rn，式0成立，则对于满足ψ1（ξ）≥0，ψ2（ξ）≥0，…，ψp（ξ）≥0的所有ξ∈Rn，有ψ0（ξ）≥0．

本文针对给定常数γ＞0，取z（k）为待估计信号向量，设计一个渐近稳定的弹性H∞滤波器：

式中Af，Bf，Cf，Df为弹性滤波器的待定系数矩阵．渐近稳定弹性H∞滤波器反馈环节不确定性BiΔKi＝Wi1Δi（t）Ei3，i∈I．

定义 ˜χT（k）＝［χT（k）＾χT（k）］，则滤波误差动态系统方程如下：

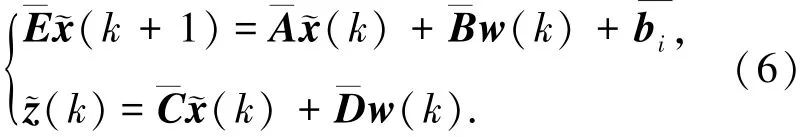
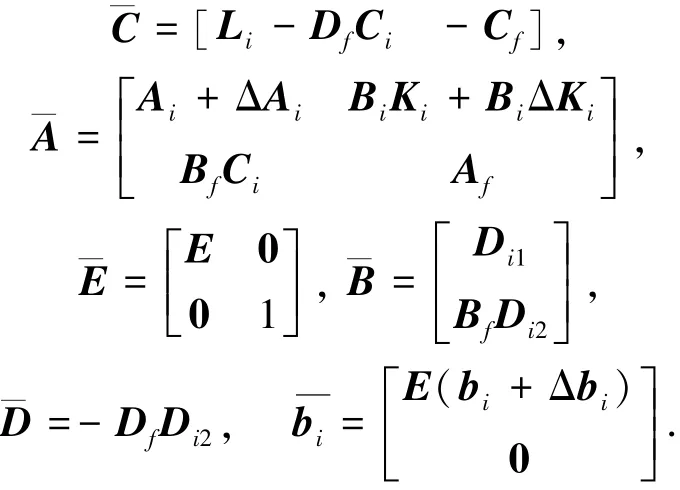
式中：Ki为反馈控制增益，则本文所考虑弹性H∞滤波器设计问题是寻求滤波器（5），使得滤波动态误差系统（6）是渐近稳定的，且扰动w到估计误差˜z（k）＝z（k）-＾z（k）传递函数的H∞范数小于给定的常数γ．

2 主要结果

在本文中，假设系统输入矩阵Bi，i∈I是列满秩的，做此假设后，则可以找到一组转换矩阵TBi∈Rnχ×nχ，i∈I，满足：

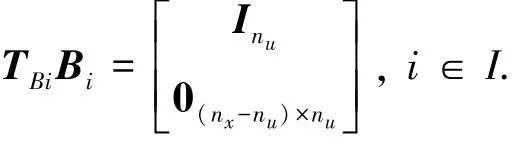
式中TBi∈Rnχ×nχ非奇异，以下弹性H∞滤波器就是基于该假设进行设计的．

定理1 考虑参数不确定离散广义分段仿射系统（1），若存在对称正定矩阵另有对称矩阵标量（i，j）∈Ω｝，实数γ∈R，∈Ω｝，以及滤波器待定参数矩阵，使得：

成立，则存在H∞渐近稳定弹性滤波器（5），使得滤波误差动态系统（6）是容许的，且扰动w到估计误差传递函数的H∞范数小于给定的常数γ．

证明 首先，通过滤波误差动态系统（6）的系统描述寻求适当的Lyapunov函数.选取广义分段仿射Lyapunov函数：

进一步构造ΔV（k）：

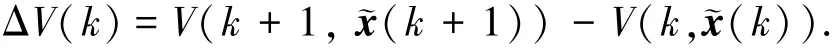
基于Lyapunov函数的定义，在零初始条件下，对于任意非零w（k）∈l2［0，∞），为使具有鲁棒H∞性能指标γ的滤波误差动态系统（6）是渐近稳定的，则只需保证以下不等式成立：

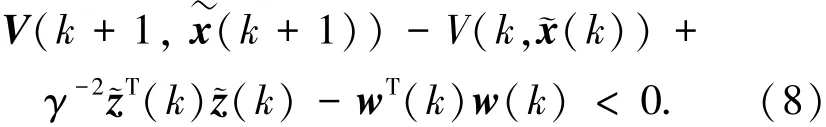
其中估计误差˜z（k）＝z（k）-＾z（k），根据系统（1）和线性滤波器（5）的定义，估计误差可进一步写成：

考虑滤波误差动态系统（6），对于任意非零w（k）∈l2［0，∞），式（8）可进一步等价于：

用矩阵形式将式（9）改写，可进一步得到：

从式（10）可以得到：

假设矩阵束（ˉE，ˉA）是非因果的．用一阶特征向量ν1和它的Hermitian矩阵ν1∗分别左乘和右乘式（11）得ν1∗ˉATPjˉAν1-ν1∗ˉETPiˉEν1＜0．

接下来根据定义1，再用ˉEν2代替ˉAν1，并注意到ˉEν1＝0，可以得到ν2∗ˉETPiˉEν2＜0．其与条件（7）相矛盾.所以矩阵束（ˉE，ˉA）是因果的．显然，证明因果性的同时也证明了矩阵束（ˉE，ˉA）的正则性．

考虑区域信息，即将式（4）带入式（10）并应用引理3，其中λij＜0，i∈I1，（i，j）∈Ω，得到：

对式（12）中各个矩阵进行合并，并先后应用2次Schur补引理，从式（13）可以得到：

另一方面，由于本文所考虑的广义分段仿射系统具有参数不确定性，为消除不确定性给求解过程带来的影响，将式（13）中的不确定性ΔAi和EΔbi分离出来，下面可以将式（13）改写为

其中做了如下定义：

进一步得到：

定理得证.

定理2 考虑参数不确定离散广义分段仿射系统（1），若存在对称矩阵H1，H3∈Rnχ×nχ，标量

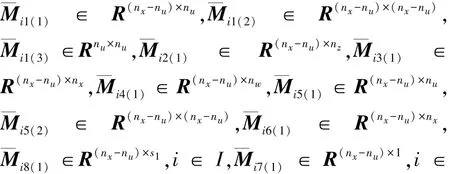
I1，使得式（7）成立，且满足以下不等式：成立，则存在H∞渐近稳定弹性滤波器（5），使得滤波误差动态系统（6）是容许的，且闭环系统（6）具有鲁棒H∞性能．

对任意矩阵N，

H∞滤波误差动态系统反馈控制器增益：

证明 首先，注意到作为定理1结论的线性矩阵不等式中，滤波误差动态系统的Lyapunov矩阵和系统矩阵相互耦合在一起，结合schur补引理，将式（14）改写：

其中：

接下来应用投影定理消除式中Lyapuno矩阵和系统矩阵的耦合，这样处理后的结果将不对滤波误差动态系统的系统矩阵进行分解，将式（17）改写为

基于投影定理，做如下变量替换：

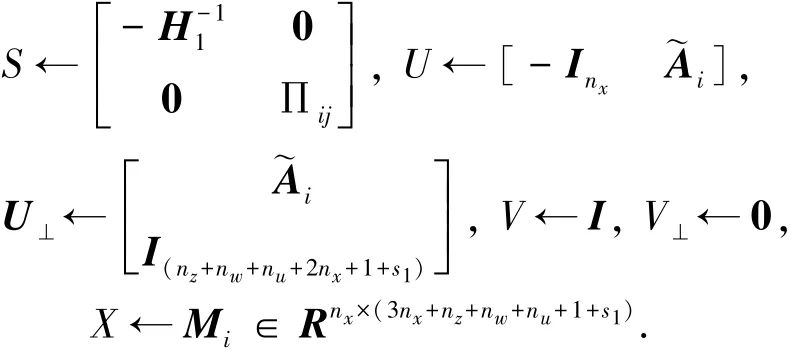
应用引理2的投影定理，得到：

对矩阵Mi∈Rnχ×（3nχ＋nz＋nw＋nu＋1＋s1），i∈I1进行分块：

将式（19）带到式（18）中，并结合所有给定矩阵的定义，最终得到式（16）．可以看到条件（16）在Ebi＝0时，就是条件（15），所以不失一般性，此处只证明式（16）成立即可，第一部分证明结束．

3 数值仿真

为了验证本文所提弹性H∞滤波器设计方法的实用性，以及定理2使得闭环系统保守性更小的结论，下面考虑一个实际物理映射，并将通过对其弹性H∞滤波器待定参数矩阵以及反馈控制增益的求取来证明结论．

以隧道二极管电路为例［18］，电容电压用χ1（k）表示，电感电流用χ2（k）表示，流过隧道二极管的电流用χ3（k）表示．将扰动输入取为随时间延续不断衰减的信号：w（k）＝e-5k，则离散化得到系统模型：

式中取系统状态初始值为χ（0）＝（2.5，1，-1），其他参数取值如下：

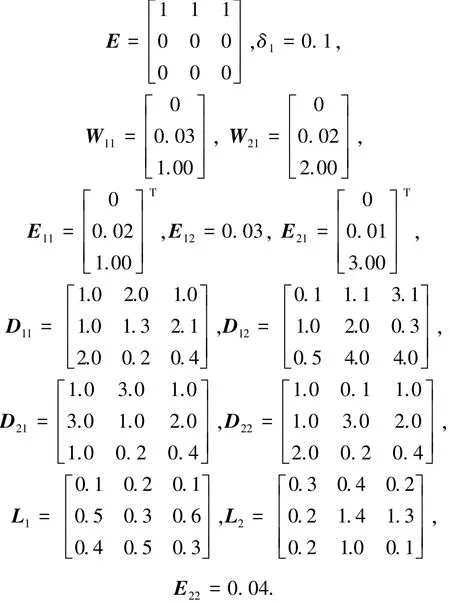
椭圆体系数矩阵通过以下公式可计算得到：

式中：α1＝3，β1＝10，α2＝4，β2＝9．

应用定理1得到一组使滤波误差动态系统（6）容许的弹性H∞滤波器反馈控制增益：

H∞干扰抑制度γ＝28.699 2．弹性H∞滤波器待定系数矩阵如下：

图1为根据定理1得到的由弹性H∞滤波器所构成滤波误差动态系统（6）的状态响应曲线：

图1 根据定理1得到的系统状态响应曲线

应用定理2得到另一组使滤波误差动态系统（6）容许的弹性H∞滤波器反馈控制增益：

H∞干扰抑制度γ＝9.145 9．弹性H∞滤波器待定系数矩阵如下：

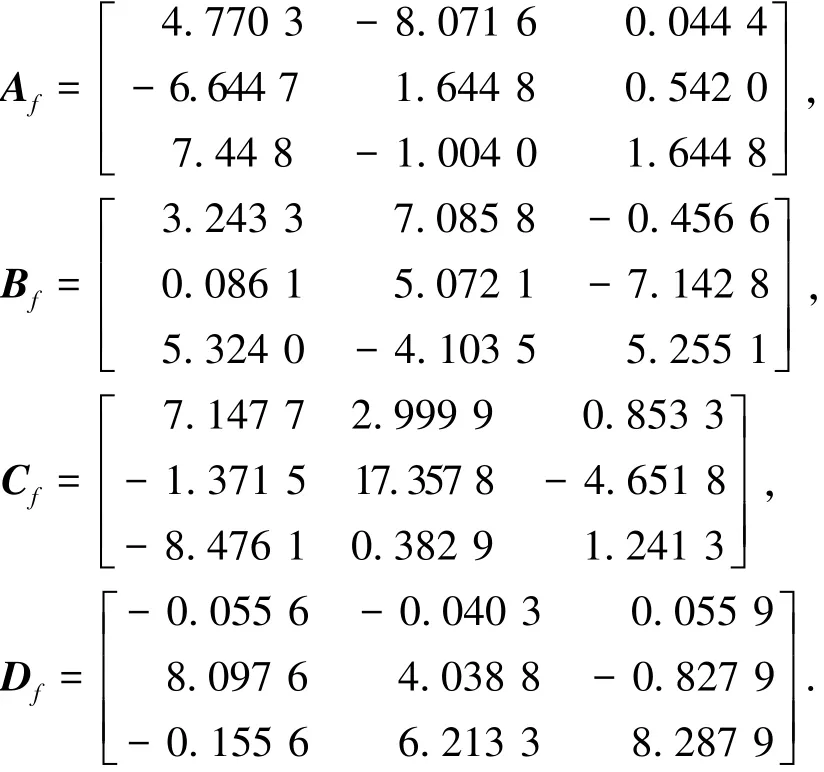
图2为根据定理2得到的由弹性H∞滤波器所构成滤波误差动态系统（6）的状态响应曲线．

图2 根据定理2得到的系统状态响应曲线

将之前给定的系统矩阵参数A1，A2再次进行赋值，其他参数不变，并重复之前步骤进行数值仿真，A1，A2取值如下：

仿真结果表明，基于定理1的控制方法不能使系统镇定，即找不到相应的弹性H∞滤波器待定系数矩阵以及反馈控制增益使得滤波误差动态系统（6）容许．而通过应用定理2，得到反馈增益

从仿真所得数据可以看到基于定理2的控制器设计方法在某些情况下确实使得系统保守性有所下降，原因在于系统矩阵和Lyapunov矩阵的耦合关系得以消除，使得这种处理方法不对系统矩阵进行分解，从而获得了保守性更小的滤波误差动态系统（6），所以相比较而言，在某些情况下，可以得到最优解.

4 结 语

本文首先构造广义分段仿射Lyapunov函数，接下来应用投影定理以及几个处理LMIs的基本引理，针对参数不确定体现为范数有界形式的离散时间广义分段仿射系统设计了使其闭环系统容许的弹性H∞滤波器，保证了由此构成的滤波误差动态系统具有一定的鲁棒性能.算法最终转化为LMIs，讨论了弹性H∞滤波器得以存在的LMIs约束条件，此种算法不对系统矩阵进行分解，并且消除与Lyapunov矩阵的耦合关系，达到减低算法保守性的目的，最后数值仿真给出了所涉及弹性H∞滤波器的最优解，同时得到滤波器控制增益.数值仿真证明了该设计方法的有效性.

［1］MASUBUCHI I，KAMITANE Y，OHARA A，et al.H∞control for descriptor systems：a matrix inequalities approach［J］.Automatica，1997，33（4）：669-673.

［2］DE OLIVEIRA M C，GEROMEL J C.A class of robust stability conditions where linear parameter dependence of the Lyapunov function is a necessary condition for arbitrary parameter dependence［J］.Systems Control Letters，2005，54（11）：1131-1134.

［3］QIU J，FENG G，GAO H.Approaches to robust H∞static output feedback control of discrete⁃time piecewise⁃affine systems with norm⁃bounded uncertainties［J］. International Journal of Robust and Nonlinear Control，2011，21（7）：790-814.

［4］HU Zhonghui，ZHU Huanyu，ZHAO Jiemei.Further results on H∞filtering for a class of discrete⁃time singular systems with interval time⁃varying delay［J］.Circuits，Systems，and Signal Processing，2013，32（3）：1081-1095.

［5］FENG Xiaoliang，WEN Chenglin，XU Lizhong.Finite horizon H∞filtering for networked measurement system［J］.International Journal of Control，Automation and Systems，2013，11（1）：1-11.

［6］JUN Yoneyama.Robust H∞filtering for sampled⁃data fuzzy systems［J］.Fuzzy Sets and Systems，2013，217：110-129.

［7］LI Zuxin，SU Hongye，GU Yong，et al.H∞filtering for discrete⁃timesingularnetworkedsystemswith communication delays and data missing［J］.International Journal of Systems Science，2013，44（4）：604-614.

［8］KIM J H.Delay⁃dependent robust H∞filtering for uncertain discrete⁃time singular systems with interval time⁃varying delay［J］.Automatica，2010，43（6）：591-597.

［9］KIM J H.Delay⁃dependent approach to robust H∞filtering for discrete⁃time singular systems with multiple time⁃varying delays and polytopic uncertainties［J］. InternationalJournalofControl，Automationand Systems，2010，8（3）：655-661.

［10］LU Renquan，XU Yong，XUE Anke.H∞filtering for singular systems with communication delays［J］.Signal Processing，2010，16（4）：1240-1248.

［11］DONG J，YANG G H.Robust static output feedback control for linear discrete⁃time systems with time⁃varying uncertainties［J］.Systems and Control Letters，2008，57（2）：123-131.

［12］ZHU X，YIN X M.Robust H＿infinity filtering for discrete⁃time systems with nonlinear uncertainties.2006 1st IEEE Conference on Industrial Electronics and Applications.Piscataway：IEEE，2006：829-834.

［13］DONG J，YANG G H.Static output feedback control synthesisforlinearsystemswithtime⁃invariant parametric uncertainties［J］.IEEE Transactions on Automatic Control，2007，52（10）：1930-1936.

［14］WANG Mao，WEI Yanling，QIU Jianbin.Static output feedbackcontrolofdiscrete⁃timepiecewiseaffine singular systems［J］.Journal of Harbin Institute of Technology，2013，45（3）：14-21.

［15］HSIUNG K L，LEE L.Lyapunov inequality and bounded real lemma for discrete⁃time descriptor systems［J］.IEEE Proc⁃Control Theory，1999，146（4）：327-331.

［16］BOYD S，El GHAOUI L，FERON E.Linear matrix inequalityinsystemsandcontroltheory［M］. Philadelphia，PA：SIAM，1994.

［17］DY Baozhu.Guaranteed cost control for uncertain singular systems［C］／／Control and Decision Conference（CCDC），2011 Chinese.Mianyang：［s.n.］，2005：37-40.

［18］RODRIGUESL，BOYDS.Piecewise⁃affinestate feedback for piecewise⁃affine slab systems using convex optimization［J］.Systems and Control Letters，2005，54（9）：835-853.

（编辑 张 宏）

Design of resilient H∞filter for discrete⁃time piecewise⁃affine singular systems

ZHOU Zhenhua1，WANG Mao1，WANG Xuehan2

（1.Space Control and Inertial Technology Research Center，Harbin Institute of Technology，150001 Harbin，China；2.Gas turbine power plant，Daqing oilfield electric，230604 Daqing，Heilongjiang，China）

This paper investigates the robust admissibility analysis and resilient filter controller synthesis for a class of discrete⁃time piecewise affine singular systems with asymptotic stability which possesses H∞performance is considered in this paper，in order to eliminate the adverse effects of external disturbances and measurement noise of control system performance.By using the piecewise⁃affine singular Lyapunov functions combined with Projection lemma and some basic lemmas，an approach of designing robust H∞feedback controller is given，the conclusions ensure resilient filtering error dynamic system possessing H∞performance. It is shown that the controller gains can be obtained by solving a family of LMIs parameterized by scalar variables.The feedback controller gain and resilient filter system matrix can ensure the stability of systems and guarantee the H∞performance of the piecewise⁃affine singular systems.Finally，the practicability of the proposed methodologies is confirmed via some simulation examples.

piecewise⁃affine singular systems；resilient filter；piecewise Lyapunov function；LMIs

TH13

：A

：0367-6234（2014）01-0008-09

2013-11-29.

国家自然科学基金（61004038）.

周振华（1983—），男，博士研究生；王 茂（1965—），男，教授，博士生导师.

周振华，zhouzhenhua99＠gmail.com.