渤海湾风浪预报数值模式的研究

李大鸣，潘 番，罗 浩，解以扬

（1.天津大学水利工程仿真与安全国家重点实验室，天津300072；2.天津市气象科学研究所，天津300074）

渤海湾风浪预报数值模式的研究

李大鸣1，潘 番1，罗 浩1，解以扬2

（1.天津大学水利工程仿真与安全国家重点实验室，天津300072；2.天津市气象科学研究所，天津300074）

为提高渤海海域海浪数值预报工作的精度，从风浪模式的角度，借助SWAN模型的物理过程，针对风输入项中线性系数的改进进行了论证。与荣城站观测结果对比表明，默认线性系数0.001 5较为合理。结合Komen、Janssen和Westhuysen 3种不同风指数增长表达式和对应的白浪破碎表达式，设计和研究不同组合方案下，风浪模式在渤海湾海数值模拟中的适用性。3个方案模拟的波浪特征值与实测值进行比较，结果显示，有效波高值与实测值变化趋势相同，模拟平均周期均偏小，且Westhuysen方案模拟效果最好。在计算结果统计分析中，模拟结果与实测值的相关系数相差不大，模拟效果较理想。

渤海湾；风浪模式；预报数值模式；SWAN模型；WRF模式；风能输入；白浪耗散

随着社会的不断发展与进步，灾害性海浪这种不可忽视的自然灾害，愈发得到人们的关注，其中与灾害性近岸波浪的接触最为直接与频繁。灾害性近岸波浪对于近海的海岸基础建设、工业生产作业、渔业养殖捕捞等相关行业有着深远的影响，与我国海洋社会经济领域的健康发展密不可分。因此，研究海浪的形成发展传播，进行海浪数值模拟，对波浪要素的实时预报具有重要意义。文中采用浅海、近岸海浪模式—SWAN模式，用于海岸、湖泊和河口的波浪模拟。基于欧拉近似的动谱平衡方程，考虑了影响海浪生成、发展的较多物理过程，还包含了当前海浪预报的较新成果。

国外对于SWAN模型的应用较早。Guan Changlone等［1］利用NDBC国家数据浮标中心的浮标数据，模拟了发生在卡罗莱纳州海岸的两次飓风过程。拟合结果与浮标数据资料对比表明，Komen形式比Janssen形式模拟效果更好。Ge Yijun等［2］从Komen、Janssen和Westhuysen 3种不同风输入方案的角度，对强台风Winnie引起的波浪进行模拟对比试验。与其他2种方案相比，Westhuysen方案的模拟误差最小。W.C.Dragani［3］等在对SWAN模型评估中，得出模拟波高低于实测值波高，在低风速情况下尤为显著的结论。

国内SWAN模型以往主要应用于东海、南海和台湾海峡3个海域的台风浪研究中，而现今也逐渐应用于渤海海域［4］。贾晓等应用SWAN模式，模拟了恒定风速和台风风场下的渤海海域波浪分布，通过模拟波高和海上测站波高比对，发现大风速条件下模拟波高偏大，于是提出修改模式中的参数，并验证了修改风能输入项后的模拟结果更接近于实测值［5］。杨德周等人应用SWAN模式，模拟渤海海域在风速小于30 m／s情况下的波浪场，并与实测值比较，结果显示，模拟的最大有效波高偏小［6］。于是提出改进模式中风输入的线性增长系数，修改后的模拟结果更接近于实测值。本文借助SWAN模型中的3种风能输入指数表达式和对应的3种白浪破碎表达式，进行试验、选择，以便获得适用于渤海湾的风浪数值模式。

1 风能输入与白浪耗散

1.1 风能输入

SWAN模式内部，同时引入了基于风-波相互作用的Miles切流不稳定机制和Phillips共振机制，描述海面风向波浪的能量转移，使能量转移模拟更加合理。Miles切流不稳定机制考虑的是波浪随时间的指数增长，而Phillips共振机制考虑的是波浪随时间的线性增长［7］。综合这2种机制，SWAN模式内部风输入项为线性增长和指数增长之和：

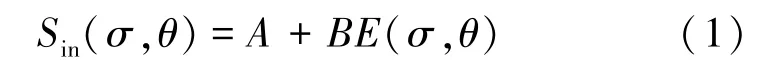
线性增长A计算公式如下：

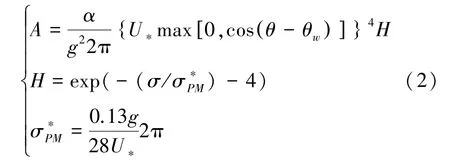
式中：α为Pillips线性增长系数，H是估值过滤因子，σ为平均频率，是全发展海况的波谱峰值频率，θw是风向，θ为平均波向，U∗为摩阻风速。

在SWAN40.85版本的模式中，选取了3种风输入能量转移的指数增长形式［8］，即常用的Komen和Janssen形式，以及较新的Van der Westhuysen形式。

1.1.1 Komen形式

该形式下的表达式［9］为U∗／cph的函数：

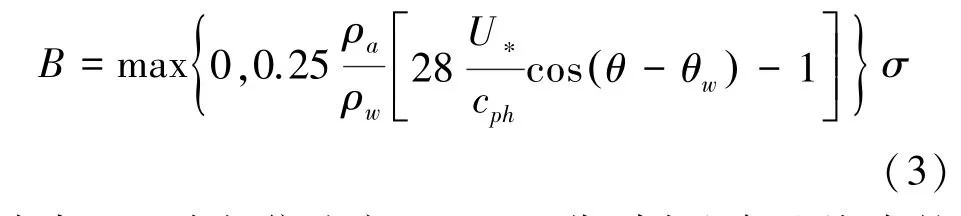
式中：cph为相位速度；ρa，ρw分别为空气和海水的密度；θw为平均风向。

1.1.2 Janssen形式

Janssen形式［10］基于拟线性波理论，表达式为

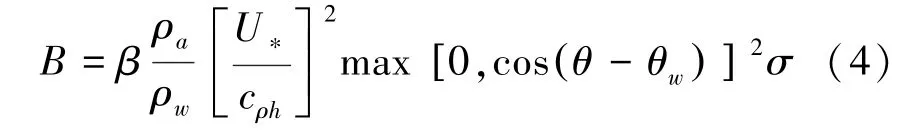
式中：β为Miles常数，可由无量纲临界高度λ确定：

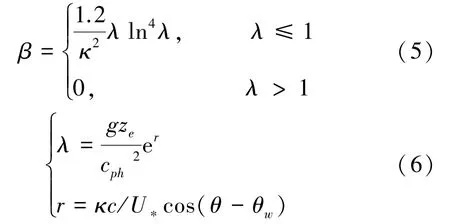
式中：κ是Karman常数，取0.41；ze是海面有效粗糙度；U∗可以由给定的海面10 m风速U10和风能量谱密度E（σ，θ）确定：

式中：z0是海面粗糙度，α＝0.01，海面有效粗糙度ze依赖于z0和海面状况，τw为波引发的压力，τ为总表面压力。

1.1.3 Van der Westhuysen形式

Van der Westhuysen形式［11］修改于Yan（1987年）的指数增长形式，提出的第3种指数增长计算方式表达式如下：

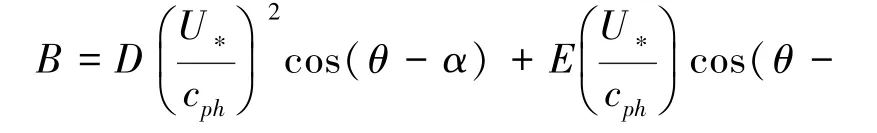
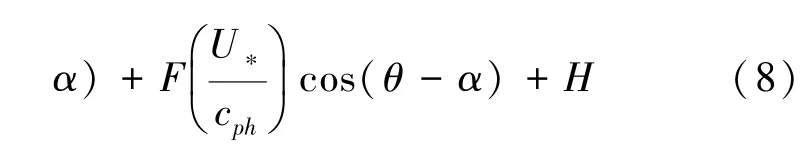
式中：D、E、F、H为常数有效系数。为了提高波浪在成熟期的增长进度与Snyder曲线的拟合度，Van der Westhuysen等将有效系数取值修改为D＝4.0×10-2，E＝5.52×10-3，F＝5.2×10-5，H＝-3.02×10-4。

1.2 白浪耗散

在SWAN海浪模式以及其他的第3代海浪模式中，最早都使用Hasselmann脉冲原理，计算白浪破碎引起的能量耗散，该表达式由波陡控制［12-13］。WAMDI Group重新确定了白浪耗散计算表达式，使之可以应用于有限水深情况，具体计算公式如下：

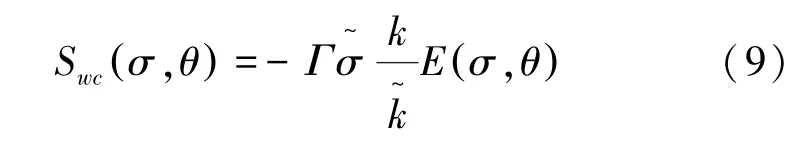
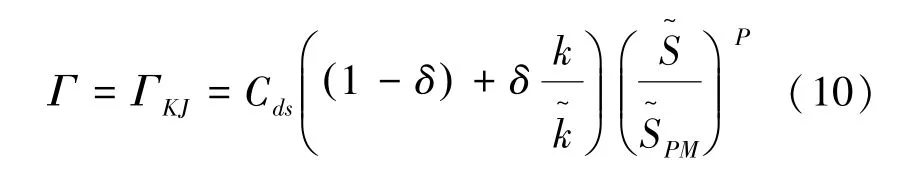
式中：Br为常数，表示饱和门限参数，取值1.75× 10-3；指数p控制耗散项的能量谱频率缩放，取值范围为2～4；Cg表示波群速度，k表示波数。

2 模式设置与检验

目前SWAN模式主要针对台风过程这类大风速条件下的风浪模拟，而渤海地区在太平洋海洋气团和东亚北部大陆气团影响下，形成季节性风环境，故需检验SWAN模式中物理过程参数是否适用于季风条件下波浪发展，因此选择黄、渤海区域进行模式试验。

2.1 计算海区

本次试验计算范围为黄、渤海区域，即东经117.35°～127.38°，北纬35.07°～41.119°。模型矩形网格分辨率为0.1°×0.1°，网格节点101×61。计算区域如图1所示。

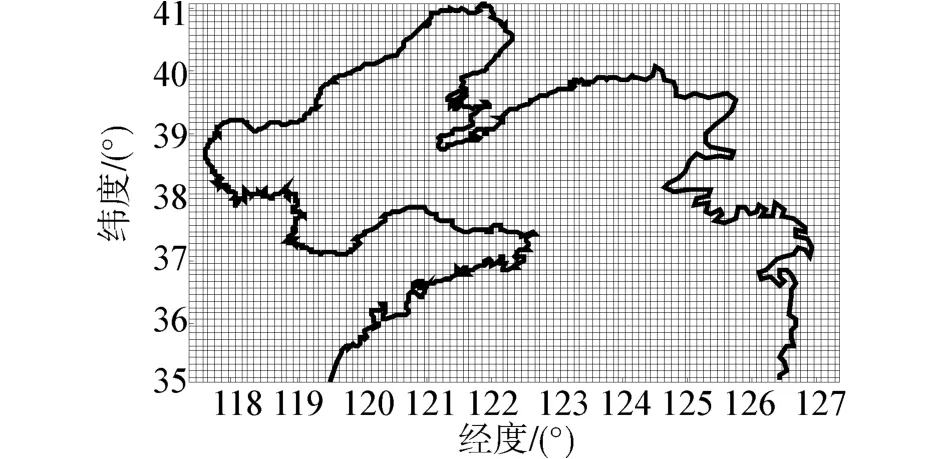
图1 计算区域的网格划分Fig.1 Grid division of the computational region

2.2 地形资料

计算区域的海底地形数据来源于美国地球物理中心（U.S.National Geophysical Data Center）发布的ETOPO地形高程数据，精确到1·′。

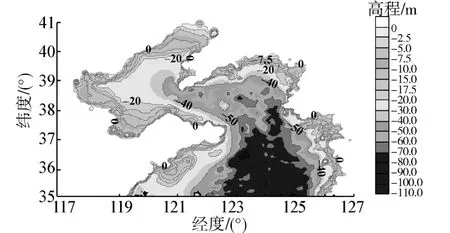
图2 黄、渤海地形等值线Fig.2 Contour for the terrain of Huang-Bo sea

图3 黄、渤海三维地形Fig.3 Three-dimension graph for the terrain of Huang-Bo sea

经过数据转换，插值处理后，绘制区域内插值后的地形等值线图和三维地形图，分别如图2、3所示。

2.3 风场资料

本次风浪模式计算中，仅以风场作为海浪的驱动场，采用以完全可压的非静力预报模式可进行二次开发的开源软件—WRF为基础模型的TJ-WRF中尺度风场数值预报系统。基于V3.4.1版本WRF模型的TJ-WRF风场预报系统，小区域针对天津全境，时间分辨率设定为1 h，垂直分辨率51层，预报时效为3 d。采用粗、细网格两重嵌套，粗、细网格水平分辨率分别为5 km和1 km。中心点为（N40°，E115°），格点数分别为441×369和151×169，采用的投影方式为兰伯特投影。

利用WRF模式中的WRF-DA数据同化模块，即同化常规观测数据、卫星遥感辐射数据和多普勒雷达数据等多种观测数据［16-17］，对各种地面、高空观测资料进行预处理。由于大范围区域初值很难通过观测获得，但是为获得较好模拟效果需要一个准确初值，这种获取初始条件的方法称为数据同化。TJ-WRF模式中包含三维变分同化3D-Var和四维变分同化4D-Var两种数据同化方法，该变分数据同化的计算方法是通过迭代算法，求解指定的目标函数，以获取一个对真实状态的最优估计。

对WRF模式预报的6级以上大风效果，采用国家气象局规定用的检验降水预报的TS评分法和分区评分法进行检验，计算公式如下：

准确率：

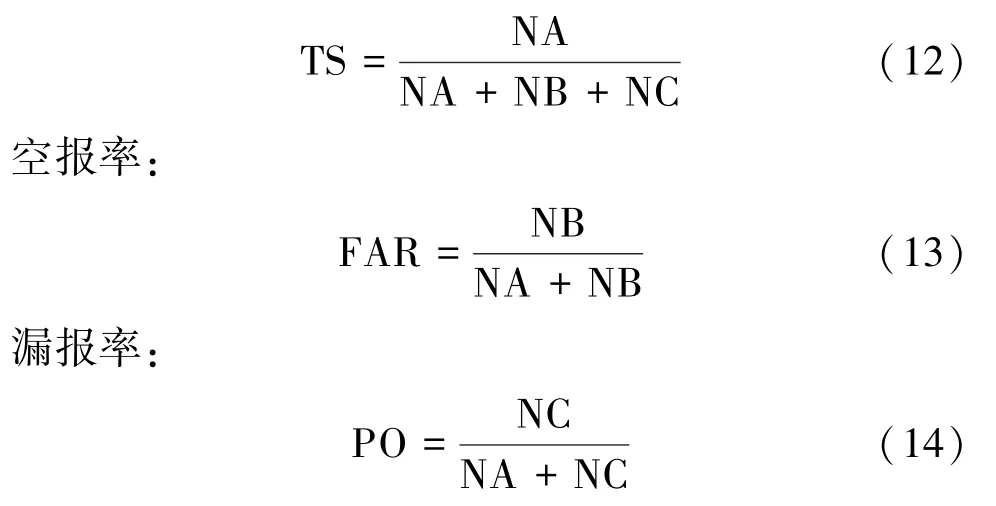
式中：NA为预报正确次数、NB为空报次数、NC为漏报次数。以实况观测为基准，如果预报风力级别与实况相同为正确，预报风力级别大于实况为空报，预报风力级别小于实况为漏报。

实况观测资料选取海上自动气象站2011年8月1日0时～2012年2月29日23时的观测资料，时间分辨率为1 h。根据自动气象站所在位置，将黄、渤海海区分为渤海区域，渤海海峡，黄海北部和黄海中部4个区域，如图4。对这4个区域的6级以上大风进行分区TS评分检验，得出24、48、72 h总体评分检验结果如表1所示。

通过对黄、渤海自动气象站观测资料6级以上大风的TS评分检验，可知对于海上6级以上大风的预报，WRF模式预报偏小的概率大于准确率，且各个分区的预报结果随着时间的延长，预报准确率下降，漏报率增大，平均误差增大。3个计算时段预报分区检验中，准确率最高的是渤海海峡，准确率最低的是渤海。

表1 总体TS评分检验结果Table1 Test result of the the whole TS method

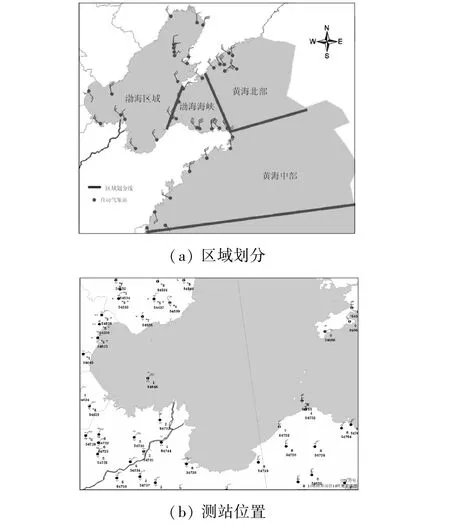
图4 自动气象站位置和区域划分Fig.4 Location of automatic weather station and area division

在黄、渤海区域（N30°～41°，E116°以东）内，有3个具有实测资料的海上浮标站可用，分别是54772（黄海北部，荣城，N37.5°，E122.5°）、54641（渤海西部，曹妃甸，N38.85°，E118.55°）和54558（渤海中部，绥中，N39.35°，E120.58°），测站分布如图5。

图5 海上浮标站分布Fig.5 Distribution of offshore buoys

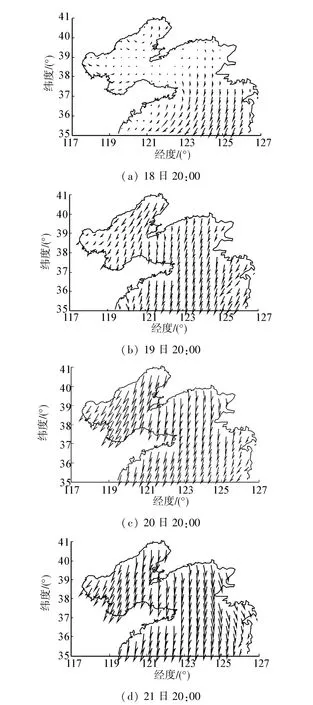
图6 72 h风场过程Fig.6 Process diagram of wind field in 72 hours

因此，为了比较风场驱动下的海浪嵌套模式模拟结果，选择数据资料较全，参考价值较高的测站，即渤海海峡附近观测站荣城站，进行参数化方案结果检验。

在利用天津市气象科学研究所的TJ-WRF模式，预报风场模型结果中，选择2012年1月18日20时至1月24日20时，2个连续3天风场过程进行SWAN海浪模式初步运行、矫正。每隔24 h绘制海面风场图检查风场过程是否合理，计算区域6个时刻风场过程如图6所示。验证风场模型，通过将风场图与实测风场数据比较，风场的大小与方向与实测一致，结果合理可靠。

3 参数选取与试验设计

在仅以风场作为驱动条件的海浪计算中，风能是海浪成长的唯一能量，风能与海浪间能量传递的过程决定海浪成长过程以及最终状态，为尽可能准确模拟风浪，需要检验并调整适用于渤海湾风输入形式及相应方案。根据风输入项的组成，将风输入项拆分为线性增长项和指数增长项分别进行验证。在确定线性增长取舍的情况下，比较3种指数增长形式哪种更适用于渤海区域海浪模拟。

3.1 线性增长

在SWAN模式预设条件下，风输入不考虑线性增长项，为比较线性增长项对波高计算的影响，设计以下3套比较方案：线性增长系数分别设α＝0、α＝0.001 5和α＝0.03，风输入指数增项选择Komen参数计算。

在模式输出结果中，选取2012年1月20日18时，一个波高较大的时刻，绘制区域波高分布图，结果分别如图7所示。

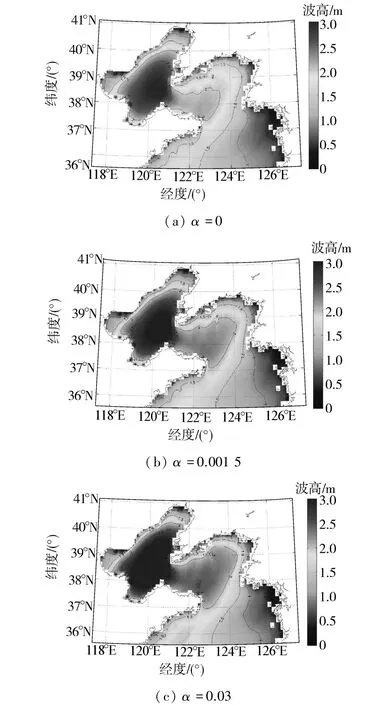
图7 不同线性增长系数下的波高分布Fig.7 Distribution of the wave height with different linear growth coefficients

根据天津气象局划分的波高等级，如表2。选取α＝0和α＝0.001 5两种参数方案，计算所得波高值分别为H1和H2，比较上述两种参数下同一点的波高等级，波级统计如表3所示。

观察表3，在有无线性增长项情况下，波高在达到2 m时，对应风级属于劲风，线性增长项的影响明显，波高差值最大达到0.24 m。在微风状态下，波高相差较小，仅有0.076 m。在区域范围内波高分布图几乎完全相同。因此增长系数为0.001 5情况下，线性增长项对波高影响较小，即Phillips空气湍动和波动效应对波浪发展影响较小，在波浪发展中基于风和波相互作用的Miles反馈机制起到决定作用。波高越高，湍流和波动效应即指数增长效应对波浪影响越来越大。

表2 波高分级表Table2 Grade of wave height

表3 线性增长系数α对波高影响Table3 Effect of wave height on linear growth coefficientα

以荣城测站为例，根据测站波高与模拟波高比较，如图8。在加入风输入线性增长项后，模拟波高最大值与实测值更接近。综合考虑整体拟合程度，采用SWAN40.85版本中默认的线性增长系数0.001 5，加入风输入线性增长项，有利于提高小波高模拟的精度，但是较大波高的情形需要依靠指数增长项调节。

图8 荣城测站波高比较Fig.8 Comparison of wave heights in Rongcheng station

3.2 指数增长

针对风输入项和白浪破碎项不同方案设计试验，研究各个方案对波浪成长的影响，找出最适合渤海湾风浪模拟的计算形式，本次试验组合方案如表4所示。

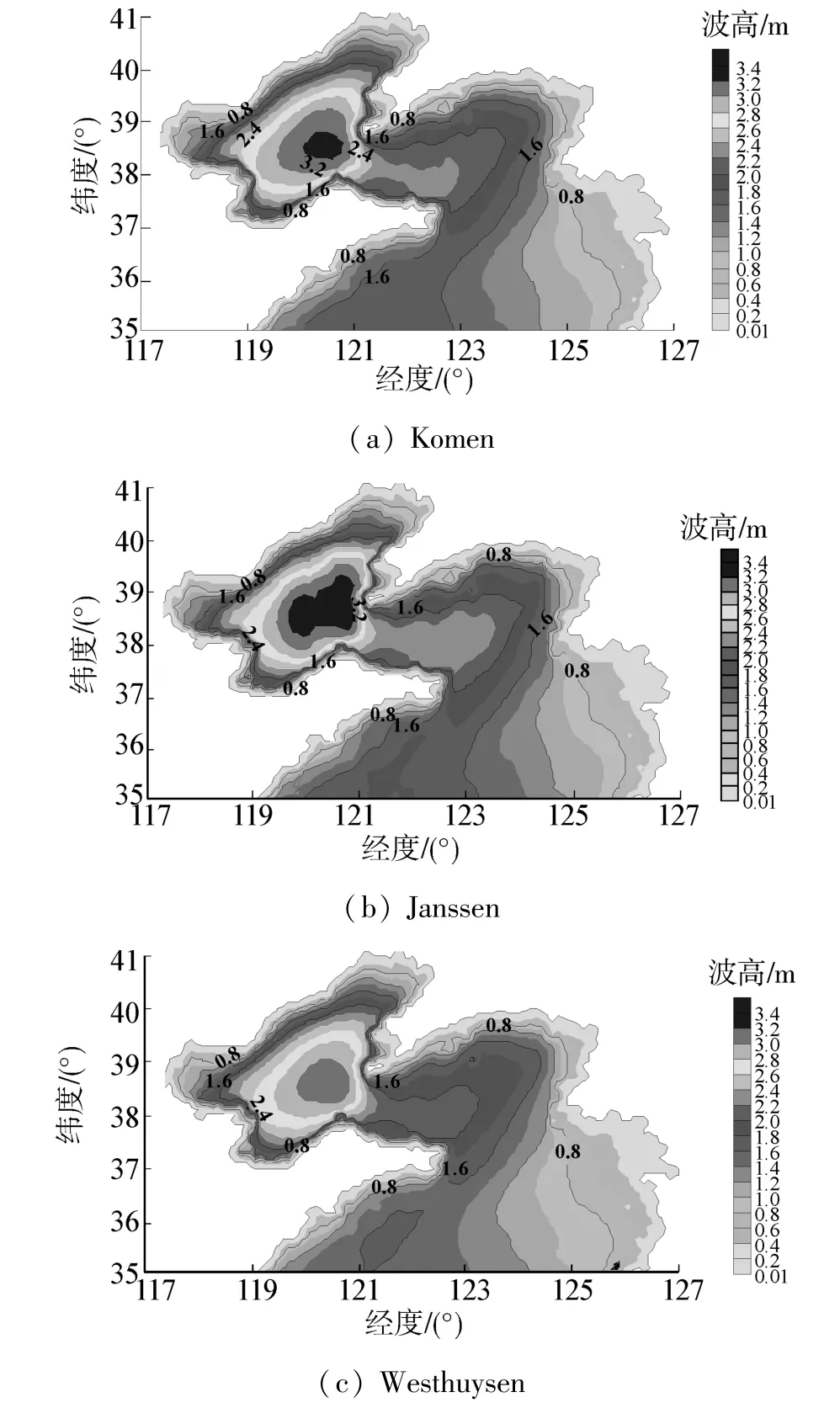
图9 不同方案波高等值线图Fig.9 Contour of wave height in different programs

表4 风输入、白浪破碎计算方案表Table4 Computational scheme of wind input and whitecapping dissipation

在上述的方案中，各个物理过程的参数除线性增长系数α取0.001 5外，其他均采用预设值。SWAN模式计算时间为2012年1月18日20时至2012年1月24日20时，2个3天过程。计算结果输出时间间隔设定为1h，在计算结果中，选取2012年1月20日16时输出的有效波高值，绘制波高分布图，进行参数方案比较。Komen参数化、Janssen参数化和Westhuysen参数化3套方案，得到计算区域海浪波高分布，分别如图9所示。

4 模拟结果检验与分析

在第3代波浪模式中：波浪的特征量分别根据作用量谱的某阶矩计算。有效波高采用作用量谱的零阶矩计算，平均周期采用作用量谱的二阶矩和作用量谱的零阶矩进行计算。为准确比较3种参数方案适用性，选取研究区域内的海上浮标如图4，对波浪观测结果进行点-点检验。

4.1 测站点-点结果检验

以荣城站为例，3套参数化方案下的模拟与实测的比较图，如图10和11所示。

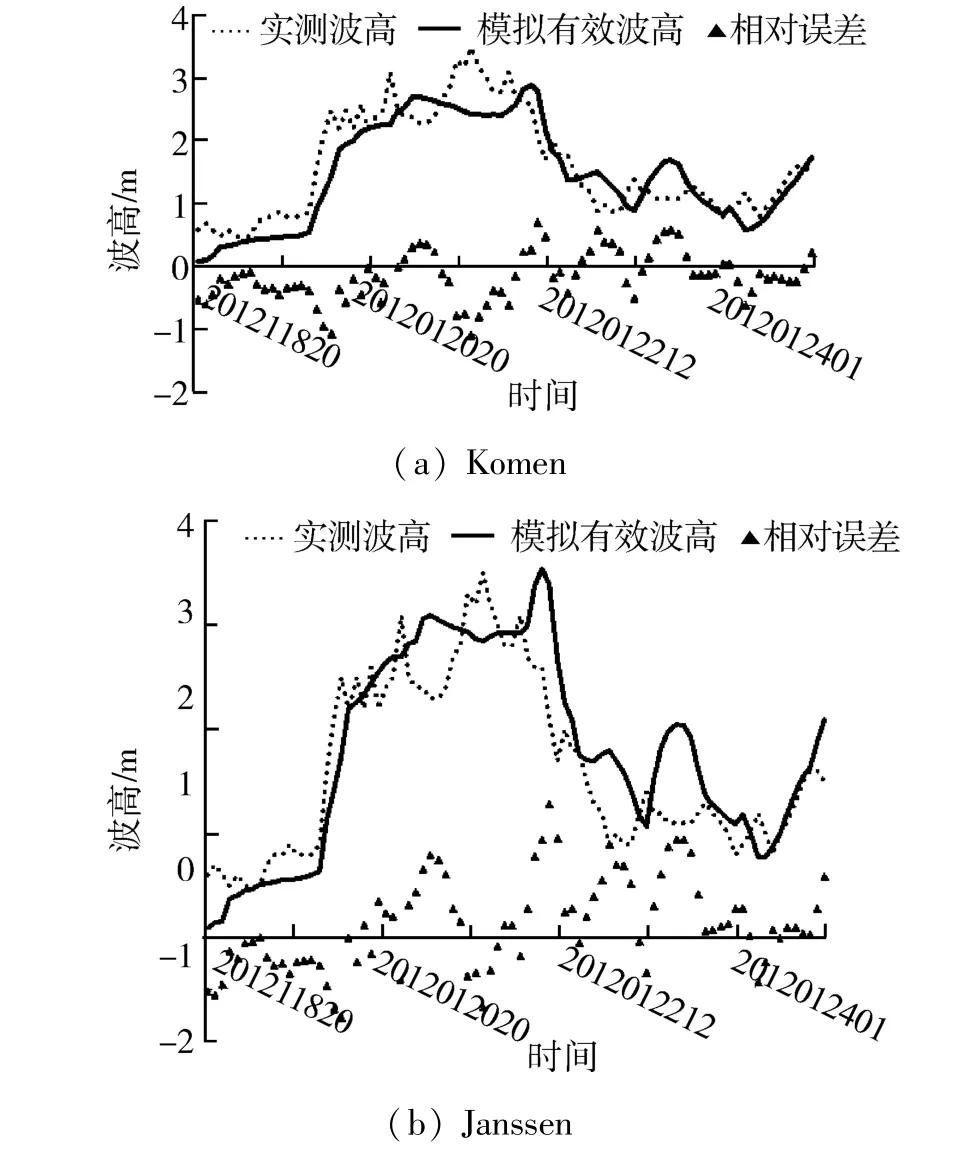
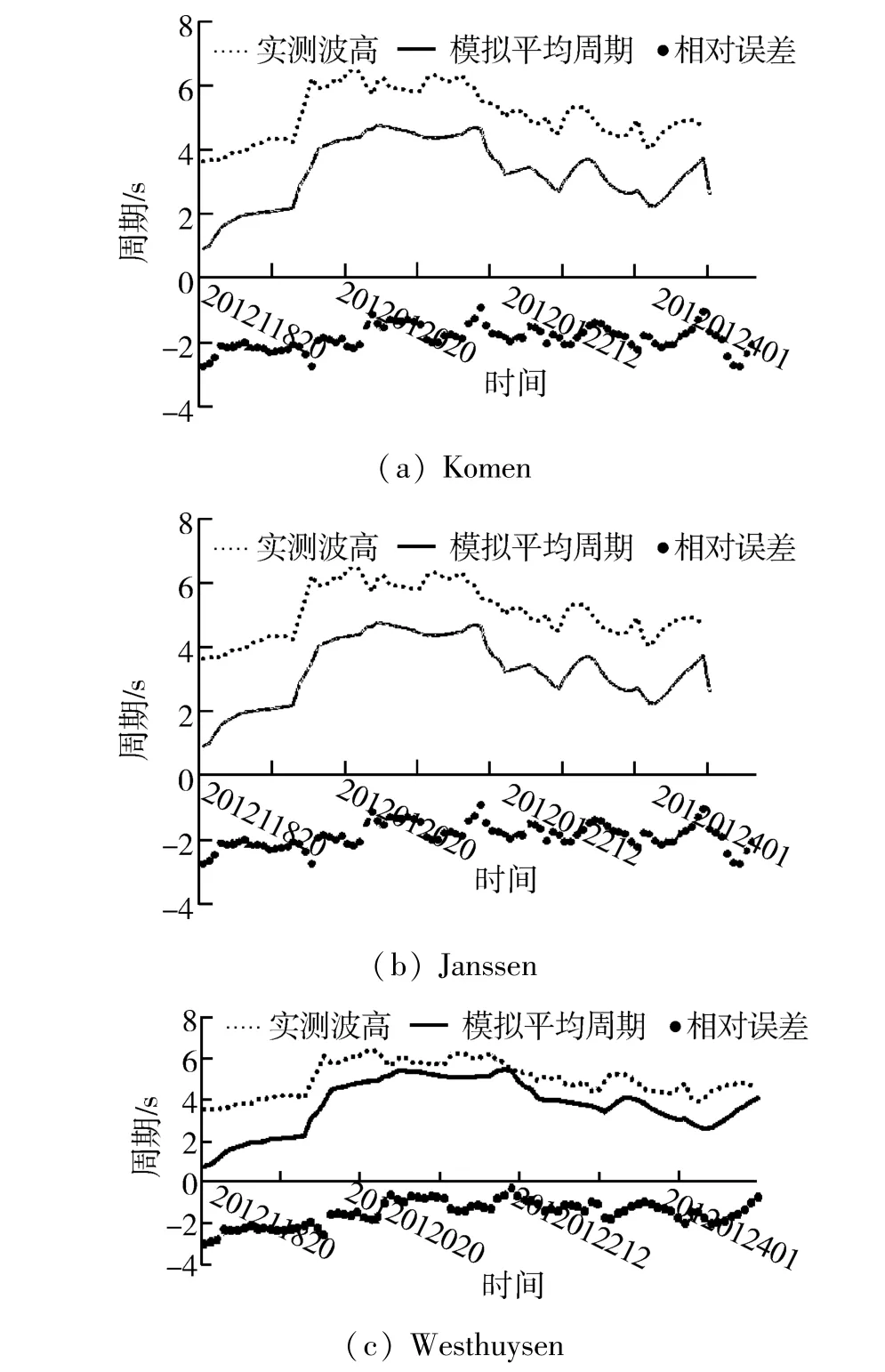
图11 不用方案模拟与实测平均周期比较Fig.11 Comparison of average period between simulated and measured in different programs

4.2 统计分析检验

根据统计分析计算公式，进行输出结果和观测资料样本统计分析，定量分析3种组合方案的适用性，找出最适用于渤海湾海浪的计算模式。

荣成站在3个参数化方案下的有效波高、平均周期计算结果统计误差由表5所示。

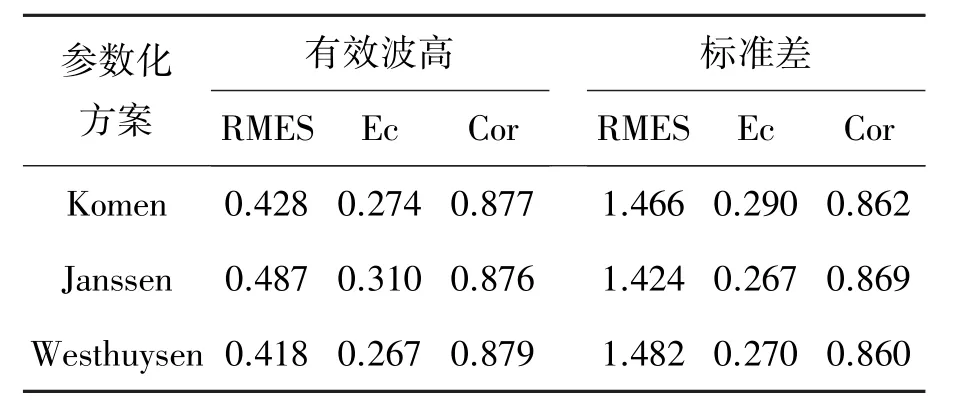
表5 荣城站参数化方案统计结果比较Table5 Comparison of statistical results in parametric schemes in Rong Cheng station

5 结论

1）在3幅计算区域指数增长波高等值线图中，波高最大值和波高较大值分布范围有明显区别，说明3个方案由于采用不同风能输入和海浪耗散理论，对计算得出波高极值的影响较大。

2）在荣城测站不同方案的有效波高比较图中，开始时刻，模拟波高总体偏小。随着计算时间的延长，模拟波高变化趋势能够与实测符合较好。在多次的波高比较中发现，一般在计算开始24 h以后，初始条件对此时刻的输出结果影响微乎其微。

3）在荣城测站不同方案波高比较图和不同方案周期比较图中，对荣城站有效波高和平均周期模拟结果，与实测值的相关系数相差不大，分别都达到0.87和0.86，模拟效果较理想。在3个参数方案计算结果统计分析中，Westhuysen方案波高、周期误差最小，相关系数最大。因此，Westhuysen参数方案更适合于浅海海浪模拟。

研究中还存在一些问题，例如在测站模拟结果中，波峰出现与实测值比较相对延后；模拟平均周期与实测值相比，整体偏小。因此，仍然需要关注影响浅水区域波浪发展的水深诱导破碎物理过程，调整相应参数，以提高模式在浅水区域适用性。

［1］GUAN Changlong，XIE Lian.Investigation of source terms in the SWAN wave model with NDBC buoy data during hurricanes［C］／／Proceedings of the International offshore and Polar Engineering Conference.Toulon，France，2004：217-220.

［2］GE Yijun，ZHONG Zhong，ZHANG Jinshan，et al.Comparison study on wind inputand whitecapping dissipation expressions in numerical simulation of typhoon-generated waves［J］.China Ocean Engineering，2008，22（4）：635-647.

［3］DRAGANIW C，GARAVENTO E，SIMIONATO C G，et al.Campos wave simulation in the outer Río de la Plata estuar-y：evaluation of SWAN model［J］.J Waterway，Port，Coastal，Ocean Eng，2008，134：299-305.

［4］管长龙.我国海浪理论及预报研究的回顾与展望［J］.青岛海洋大学学报，2000，10（30）：549-556.

GUAN Changlong.A review of history and prospect for study of sea wave theory and its forecast in China［J］.Journal of Ocean University of Qingdao，2000，10（30）：549-556.

［5］贾晓，潘军，NICLASEN B.SWAN模型风能输入项的改进与验证［J］.河海大学学报：自然科学版，2010，38（5）：585-591.

JIA Xiao，PAN Jun，NICLASEN B.Improvement and validation of wind energy input in SWAN model［J］.Journal of Hohai University：Natural Sciences，2010，38（5）：585-591.

［6］杨德周，伊宝树，徐艳青，等.SWAN浅水波浪模式在渤海的应用研究——Phillips线性增长比例系数的改进［J］.水科学进展，2005，16（5）：710-714.

YANG Dezhou，YI Baoshu，XU Yanqing，et al.Application of the SWAN wave model to Bohai Sea：improvement of Phillips linear growth term［J］.Advances in Water Science，2005，16（5）：710-714.

［7］PHILLIPS O M.On the generation of waves by turbulent wind［J］.J Fluid Mech，1957，2：417-445.

［8］MULLIGAN R P，BOWEN A J，HAY A E.Whitecapping and wave field evolution in a coastal bay［J］.Journal of Geophysical Research，2008，113（C03008）：1-16.

［9］KOMEN G J，HASSELMANN S，HASSELMANNK.On the existence of a fully developed wind-sea spectrum［J］.Phys Oceanogr，1984，14：1271-1285.

［10］JANSSEN P A E M.Quasi-linear theory of wind-wave generation applied to wave forecasting［J］.Journal of Physical Oceanography，1991，21：1631-1642.

［11］Van der WESTHUYSEN A J.Nonlinear saturation-based whitecapping dissipation in SWAN for deep and shallow water［J］.Coastal Engineering，2007，54（2）：151-170.

［12］李玉成.波浪在浅水区的变形及破碎［J］.海洋学报，1997，19（3）：111-118.

LI Yucheng.Deformation and fragmentation of waves in shallow water［J］.Acta Oceanologica Sinica，1997，19（3）：111-118.

［13］李玉成，董国海.缓坡上不规则波浪的破碎指标［J］.水动力学研究与进展（A辑），l993，8（1）：21-27.

LI Yucheng，DONG Guohai.Breaker indices of irregular waves on gentle beach［J］.Journal of Hydrodynamics（A），l993，8（1）：21-27.

［14］BOUWS E，KOMEN G J.On the balance between growth and dissipation in an extreme depth-limited wind-sea in the southern North Sea［J］.Journal of Physical Oceanography，1983，13：1653-1658.

［15］ALVES J，HENRIQUEG M，BANNER M L.Performance of a saturation-based dissipation-rate source term in modeling the fetch-limited evolution of wind waves［J］.Journal of Physical Oceanography，2003，33：1274-1298.

［16］XIE L，LIU B，LIU H Q，et al.Numerical simulation of tropical cyclone intensity using an air-sea-wave coupled prediction system［J］.Advance in Geosciences，2008，18：19-43.

［17］LIU B，LIU H Q，XIE L.A coupled atmosphere-wave-ocean modeling system：simulation of the intensity of an idealized tropical cyclone［J］.Monthly Weather Review，2010，139：132-152.

A study of the numerical forecast model of wind waves in Bohai Bay

LI Daming1，PAN Fan1，LUO Hao1，XIE Yiyang2
（1.State Key Laboratory of Hydraulic Engineering Simulation and Safety，Tianjin University，Tianjin 300072，China；2.Tianjin Institute of Meteorological Sciences，Tianjin 300074，China）

In order to enhance the accuracy of the numerical prediction of waves in Bohai Bay，the improvement of linear coefficients for the wind input is demonstrated with the aid of the physical processes of the SWAN model，from the perspective of wave patterns.Ithas been shown that0.001 5 is a more reasonable default of the linear coefficient in contrast to the observations of the Rongcheng buoy.Combined with the three wind exponential expressions of Komen，Janssen and Westhuysen and the corresponding whitecapping dissipation expressions，the applicability of the wave mode for the numerical simulation of waves in Bohai Bay was designed and researched with different portfolio schemes.Consequently，the characteristic values and measured values of the three schemes were compared and the results showed that the effective wave height has the same change trend with the measured ones.Both of them have a smaller average cycle during the simulation.Furthermore，Westhuysen has been found to be the best one among the three schemes.With the statistical analysis of the calculation results，it has been found that there is little difference between the correlation coefficients with the simulated and measured values，so the simulation results are satisfactory.

Bohai bay；wind wave；numerical forecast model；SWAN model；WRF model；wind energy input；whitecapping dissipation

10.3969／j.issn.1006-7043.201301045

P722.4；P731.33

A

1006-7043（2014）01-0132-09

http：／／www.cnki.net／kcms／detail／23.1390.U.20131112.1005.014.html

2013-01-23.网络出版时间：2013-11-12.

国家自然科学基金资助项目（51079095）；国家自然科学基金创新研究群体科学基金资助项目（51021004）.

李大鸣（1957-），男，教授，博士生导师.

李大鸣，E-mail：lidaming＠tju.edu.cn.