基于工程反问题的圆管湍流流体热物性参数反演

梅 宁，焦 思

（中国海洋大学工程学院，山东青岛266100）

基于工程反问题的圆管湍流流体热物性参数反演

梅 宁，焦 思

（中国海洋大学工程学院，山东青岛266100）

给出一种利用测定圆管对流换热温度场求解湍流流体热物性参数的方法。根据边界层理论，对管内湍流强制对流换热控制方程组进行简化，并通过考虑湍流运输中的密度脉动，对传统的混合长度湍流模型进行改进，基于该计算模型求解圆管湍流模型的温度场。采用Levenberg-Marquardt方法通过测量温度场反演了湍流对流换热控制方程中的黏度系数。结果表明，利用反问题方法通过测定温度场反演湍流流动流体的热物性参数具有可行性，精确度较高。

Levenberg-Marquardt方法；混合长度理论；湍流对流换热；黏度系数

作为CFCs的替代物之一，由几种单质制冷剂按比例混合而成的非共沸混合制冷剂具有较为广阔的市场空间［1］。非共沸制冷剂的温度滑移特性使其在循环过程中组分逐渐偏移从而对制冷机组的性能造成影响，严重时甚至损坏机组。目前唯一的解决办法是将系统内的变质制冷剂全部抽出，再重新注入标准配比的制冷剂，显然投资巨大并且浪费资源。因此废弃制冷剂的回收再生问题显得十分迫切。目前市场上有较多的制冷剂回收再生装置，但是都不具有组分检测的功能。本文尝试寻找一种热力学方法，实现混合制冷剂的组分检测。用热力学方法实现混合制冷剂的组分检测主要包括混合流体的热物性反演和根据热物性与组分的关系求解组分2个方面内容，本文主要针对流体热物性参数反演展开研究。

湍流流动是工程技术领域与自然界中常见的流动现象，流体作湍流流动时的对流换热也是工程传热过程中最常见的一种热交换方式。关于湍流运动与换热的数值计算，是目前计算流体力学与计算传热学中困难最多因而研究最活跃的领域之一。一方面为了简化计算，湍流对流换热计算模型通常会被定为常流动模型；另一方面在旺盛湍流区内，由分子扩散引起的热物性变化相对于有湍流脉动引起的物性变化较小可以忽略不计，因此很少有人关注湍流模型中的热物性参数。本文尝试采用Levenberg-Marquardt方法通过采集的温度场对换热流体的热物性参数进行反演。

基于可观测量如温度等运用反问题方法推算混合物热参数已经有很多成熟的反问题方法：基于正则方法的Levenberg-Marquardt方法［2-3］、共扼梯度法［4-5］；对反问题经典方法正则化方法进行改进的迭代正则化方法［6］；从系统学发展形成的遗传算法、神经网络算法［7］、MCMC方法［8］以及基于广义概率的贝叶斯方法［9-11］等。传统的正则方法以其相对较小的计算量得到广泛的应用；系统学方法的很强的适应性也使其得到广泛关注；对于重复性反问题具有先天优势的贝叶斯方法，在重复假设算例中得到了进一步发展。

本文根据一维稳态热传导模型设计出可以实时测量温度数据的试验装置。运用Levenberg-Marquardt方法以及热物性参数的经验公式［12］，结合试验结果，求得实验流体的热物性参数。反演结果表明，利用反问题求解湍流流动流体的热物性参数具有可行性，为下一步分析混合制冷剂组分反演做了铺垫。

1 正问题的数学模型

光滑圆管中的充分发展湍流的平均流动有如下特点：（1）平均速度场是平行流。（2）除压强外，一切平均量只和圆管中径向坐标有关。因此本文取充分发展区的圆管湍流对流换热模型为研究对象，并做了进一步简化。

（1）忽略径向流动，将管内湍流对流换热作为一维导热型问题。

（2）管外壁通过均匀高温来流加热，铜质管壁的热阻可忽略。

（3）通过加热段之后的热电偶组测定径向节点温度，即测定管内有限节点换热稳定时无内热源温度场。

根据边界层理论，通过数量级分析，有管内湍流对流换热控制方程组：

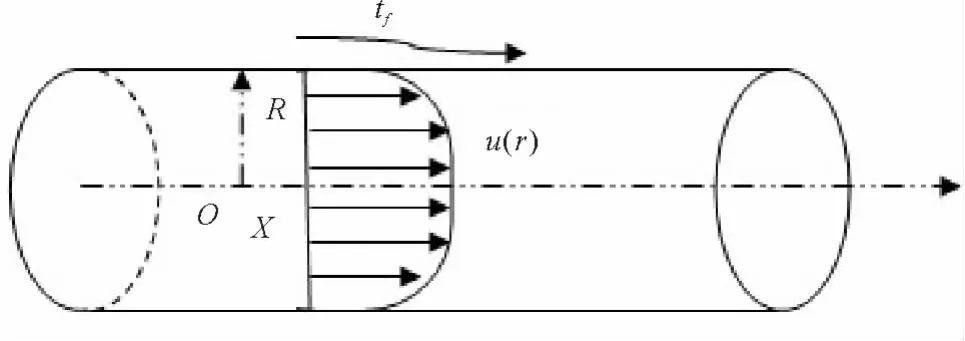
图1 圆管湍流充分发展对流换热示意图Fig.1 Diagram of heat flow model

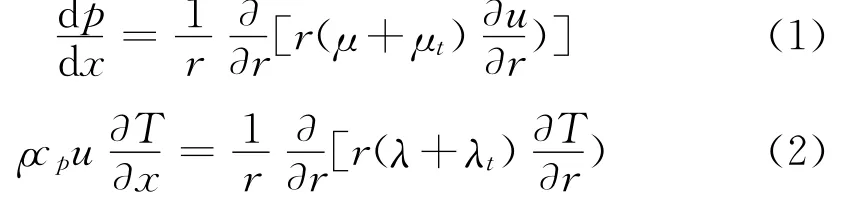
试验段内，压力变化较小，认为热物性参数仅受温度影响，上式中随温度发生变化的热物性参数有密度ρ、定压比热容cp（本文中将密度与定压比热容的乘积定义为体积热容，用C表示）、黏度系数μ、导热系数λ。实验温度范围内，黏度系数随温度的变化为Δμ／μ=18.8%，而ΔC／C=0.22%，Δλ／λ=2%，因此选择黏度系数作为热物性参数的反演目标［13］。为简化方程将随温度变化较小的体积热容和导热系数设定为常系数。

定义下列无量纲量。

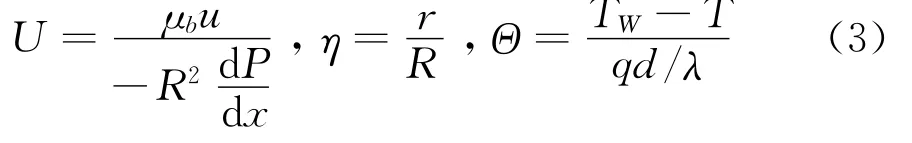
管内湍流对流换热控制方程组变为：

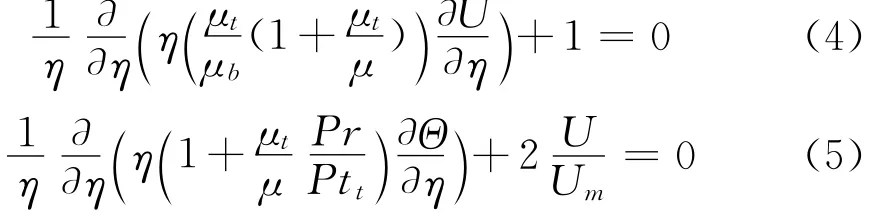
从（1）、（2）式可以看出，湍流黏性系数μt及湍流导热系数λt均为未知量，需要引入湍流模型来确定。

2 混合长度理论的变物性修正

在对流换热过程中，流体的物性随着温度的改变而改变，而温度场的变化将对流体的流动产生影响，此时速度场和温度场是相互耦合的，在实际研究过程中，若同时对流体的每个物性变化产生的影响进行分析，将使问题变的非常复杂，通常采取的办法是重点分析其中的某个物性变化，该物性的变化会引起温度场的变化，而温度场的变化又会引起整个物性场的变化。本文采取的方法是考虑密度的变化，进而得到适用于变物性计算的混合长度模型［14］。

对于直管内的二维边界层型湍流流动，考虑密度脉动，湍流应力的表达式将变成：

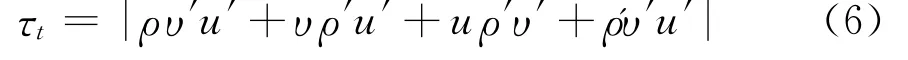
对于边界层型流动，υ的值近于零，忽略三阶脉动值乘积项，则（6）式变为：

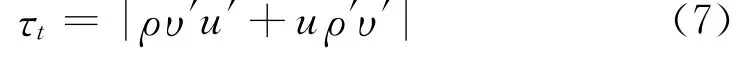
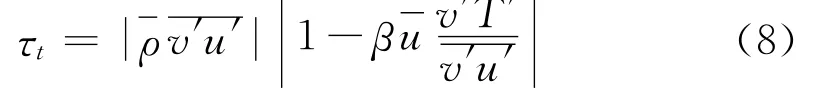
根据混合长度理论有：

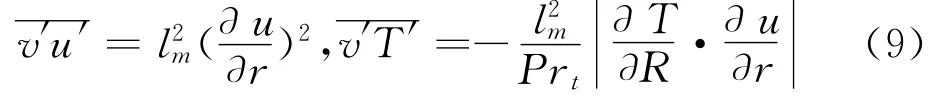
将（9）代入（8）整理得到：

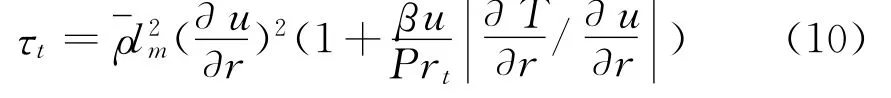
变物性流动时湍流黏性系数表示如下：

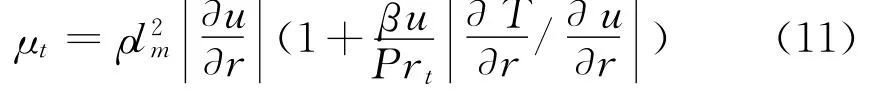
定义Fm为密度脉动时的变物性修正因子，μt，o表示原始混合长度模型计算的湍流黏性系数，

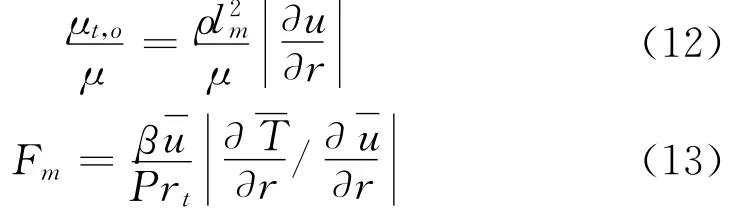
在本文数值计算中，原始混合长度湍流计算模型用Nikurades公式计算，并按vanDriest提出的阻尼函数进行修正［15］：

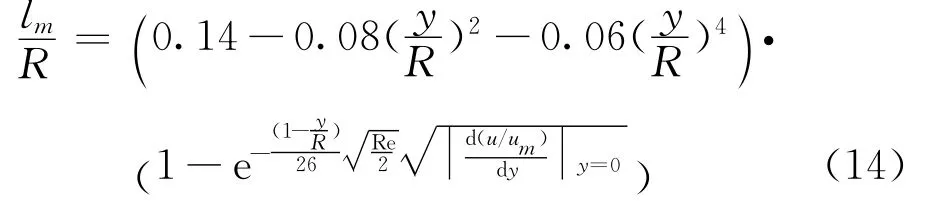
3 液体黏度的计算

液体黏度随温度升高而减小，在低于正常沸点下，液体黏度的对数值与温度的倒数近似呈线性关系：

当温度高于沸点时，lnμ与1／T关系图中出现了弯曲，上式计算误差增大。因而有以下2个公式：

对于不同的流体上述3个公式的拟合精度不同，因此对于不同的流体，选取的经验公式不同，本文选取水作为实验介质，公式（17）的拟合精度最高。记P=［A B C D］，即为待反演参数。上述公式中的A，B，C，D为系数值，可以查表得到。

应用反问题通过采集的温度场求解流体的热物性参数即为对上述系数值A，B，C，D的反演。

4 Levenberg-Marquardt方法

4.1反问题模型

Levenberg-Marquardt方法是特殊化正则方法Gauss-Newton迭代方法，它可以看作对非线性问题作先线性化后正则化的过程［16］。用来求解下述关于参数P的函数的最小值：该方法通过输入的参数P求解正问题得到Tnum并通过敏感系数矩阵对参数P进行修正。对于给定初始猜测值P0，在第k步，有如下计算式：

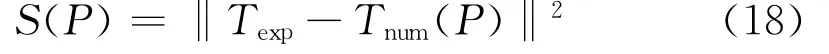
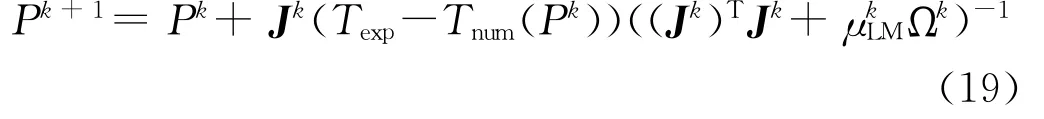
上式中的J即为敏感系数矩阵，敏感系数矩阵可采用多种方法计算，对于有确定表达形式的，可以采用微分链式法则求解。本文的敏感系数矩阵为：

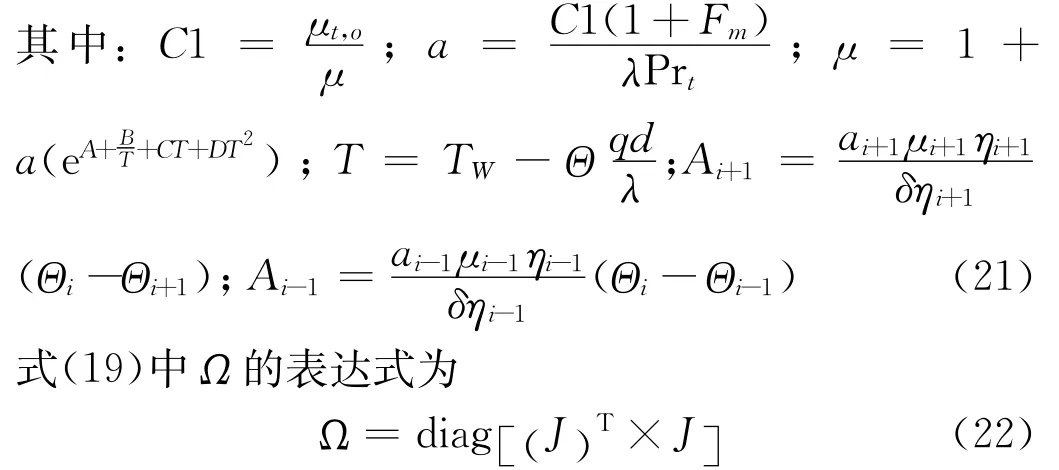
μLM为Levenberg-Marquardt参数。μLM减少了迭代过程中的震荡和反问题的不适定性，从而使得迭代过程快速的向最佳的参数P收敛。μLM的引入使得参数估计存在偏差，但随着迭代向最优参数值收敛这个误差逐渐减小并可忽略。

4.2 L-M方法迭代实施

采用L-M方法求解圆管内流体热物性参数的过程：首先测量圆管内流体的温度值；然后假设一个未知的热物性参数，在该假设下通过求解正问题得到管内流体的温度场，根据温度的测量值和计算值，计算目标函数，判断是否符合精度要求，如果不满足，则对假设的未知的热物性参数进行修正，修正后继续通过正问题求出测量点的温度值，计算目标函数，直至得到满足条件的收敛值。

假设给定初始位置的测量温度数据为Tcal，未知的热物性参数的假设值为P0，μLM的初始值为，则Levenberg-Marquardt算法的具体过程为：

图2 Levenberg-Marquardt算法的迭代程序Fig.2 Flow chart of Levenberg-Marquardt method

5 试验验证及结果分析

5.1试验台的描述

如图3所示实验装置主要有3部分组成：实验流体的循环系统，加热流体循环系统和信号采集分析系统。装置选取内径为8 mm壁厚1 mm的铜管作为实验流体的循环管道。流体速度为1.5 m／s，初始温度为291.5 K，恒温水浴加热温度为333 K。均匀的流体流经充分长的入口段进入长20 cm的加热段。管内温度由布置在加热段末端沿径向分布的4个K型热电偶采集。信号通过A／D转换器输入MATLAB2009a编写的程序中进行处理。

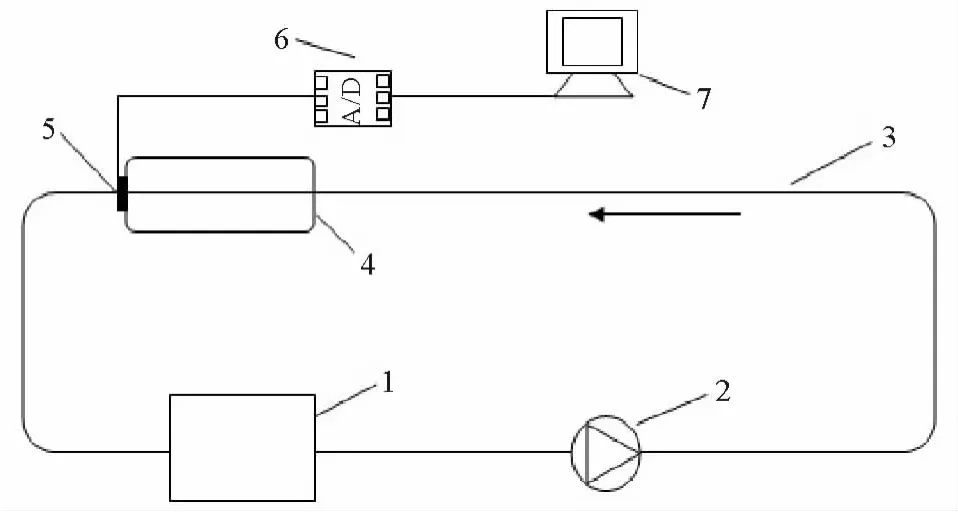
图3 实验装置示意图Fig.3 Convective heat-transfer experimental apparatus

5.2实验结果及分析

本文以水做为实验流体进行了实验。由文献［12］可知，在0～100℃的温度范围内，式（17）中的系数分别为A=-24.71，B=4 209，C=4.527×10-2，D= -3.376×10-5。表1给出了5组不同的参数初始猜测值。

表1 参数的初始猜测值Table 1 The initial value of parameters

图4、5中的曲线表示水的黏度系数在计算温度区域内（273.15～373.15K）随温度变化的关系曲线、实验拟合曲线和误差曲线。从图中曲线可以看出，反问题方法对于黏度系数能进行有效的反演，当输入不同的初始猜测值时，误差可以控制在11%内。从误差曲线可以看出该方法对于待测流体温度较高接近沸点的区域内有较高的精度。

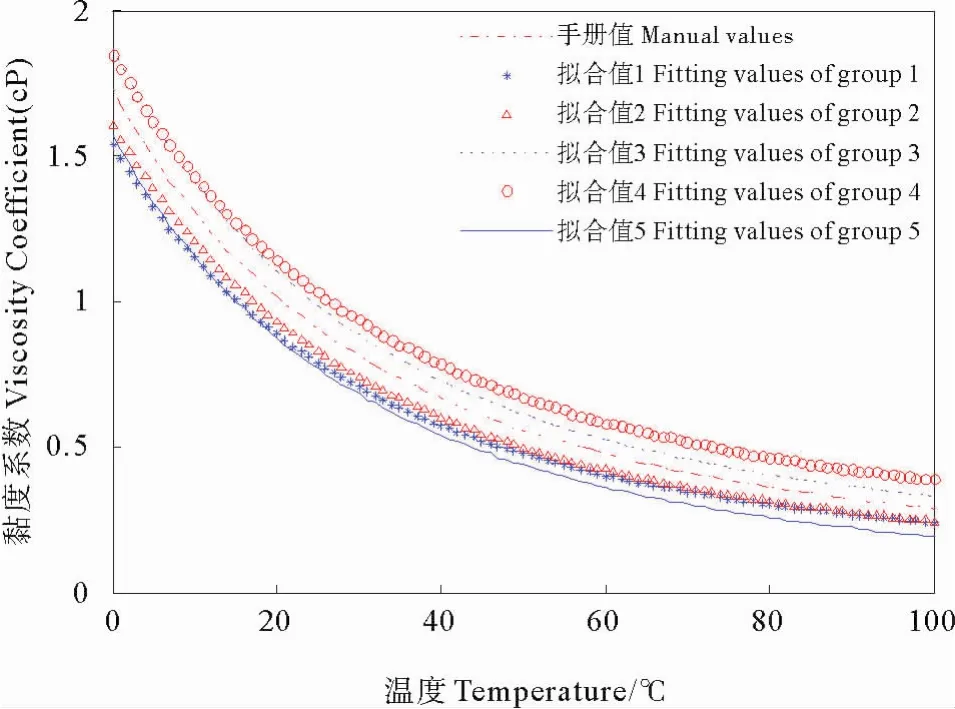
图4 不同初值条件下的拟合曲线Fig.4 Fitting parameter curves in different initial values

图5 不同初值条件下的相对误差曲线Fig.5 relative error curves in different initial values

表2给出了不同初始猜测值对应的拟合参数值及绝对误差。将第一组初值作为标准，后4组数据只变动1个系数的初值进行反演得到结果见表2。对比几组结果，可以看出当初始值偏离真实值越大时，反演得到结果的误差越大。A、B的反演误差普遍比C、D的误差小说明了反问题方法对于系数A、B的敏感性较强而对C、D的敏感性相对较弱。由1、2组结果可以看出当A的初值偏离实际值较大时，A参数反演的误差变化并不大，但是D的误差增倍；对比1、3组结果，当B的初值变大时，反演得到的其他参数的误差全部增大：A值误差由1.21%上升到3.12%，B的误差上升了1.47%，C的误差由1.13%上升到2.10%，D的误差上升了1.69%；对比1、4组结果，当C的初值偏离实际值较小时，对A的反演有一定正影响，对于B、D影响不大，但是对于自身反演误差并没有优势；对比1、5组数据可以发现，D初值的变化对于A、B的影响是相反的，但是对于自身和C的影响与C的情况是相同的。

由上可以看出反演初值对于反演结果有一定的影响，对于A、B 2个系数，初值越接近真实值，反演的精度越高，初始猜测值与真实值的偏差较大时，反演结果的误差也较大，所以在选择初值时，应尽量选择合理的初始猜测值；但是对于C、D 2个系数，初始值偏离真实值的大小对于自身的影响不成正比关系，初始猜测值与真实值偏差较小时，对A、B的反演精度有正影响。综上，合理的初始猜测值对于降低误差提高精度有一定影响，并且4个系数之间的误差关系不是独立的而是相关的，有一定的叠加作用。

表2 不同初值条件下的拟合参数值及绝对误差Table 2 Fitting parameters and absolute error in different initial values

6 结语

本文从湍流流体的热物性参数的不易确定性出发，给出了一种可以反演得到湍流流动流体热物性参数的一般方法。

根据参数的初始猜测值，利用改进的混合长度模型求解正问题得到了圆管内流体的温度场，并应用LM方法中的敏感系数矩阵对系数的猜测值进行修正直至得到满足误差的温度场和系数猜测值，根据热物性参数的半经验公式得到待反演热物性参数值。

本文的研究结果表明，利用L-M方法及局部的温度测量信息，能够对圆管充分发展区对流换热流体的热物性参数（黏质系数）进行有效的反演；反问题方法对于4个系数的敏感性不同，对于A、B的敏感性较好但是对于C、D的敏感性较差；4个系数并不是独立存在的，而是相关的，并且彼此之间的反演误差会对其他系数造成影响；合理的初始猜测值有利于降低误差提高精度。

［1］ 俞炳丰，彭伯彦.CFCs制冷剂的回收与再利用［M］.北京：机械工业出版社，2007：47-50.

［2］ Mejias M，Orlande H R B，MÖzisik.A Comparison of different parameter estimate on techniques for the identification of thermal conductivity components of orthotropic solids［C］.Washington：3rd Int Conf on Inverse Problems in Eng，1999.

［3］ SAWAF B，OZISIK N，Determining the constant thermal conductivities of orthotropic materials by inverse analysis［J］.International Communications in Heat and Mass Transfer，1995，22（2）：201-211.

［4］ Mzali F，Sassi L，Ben Nasrallah S.Optimal experiment design and simulations identification of thermo-physical properties of orthotropic solids 4th［C］.Rio de Janeiro：Int Conf on Inverse Problems in Eng，2002.

［5］ Huang C H，Wang SP.A three-dimensional inverse heat conduction problem in estimating surface heat flux by conjugate gradient method［J］.Int J of Heat and Mass Transfer，1999，42：3387-3403.

［6］ Yao J，Chia C.Comparison of Newton-Gauss with Levenberg-Marquardt Algonthm for Space Resection［C］.Singapore：The 22nd Asian Conference on Remote Sensing，2001.

［7］ 肖庭延，于慎根，王彦飞.反问题的数值解法［M］.北京：科学出版社，2003.

［8］ AndrieuC，De Freitas N，Doucet A，et al.An introduction to MCMC for machine learning［J］.Machine Learning，2003，50：5-43.

［9］ Wang J，Zabaras N.A Bayesian inference approach to the inverse heat conduction problem［J］.Int J of Heat and Mass Transfer，2004，47：3927-3941.

［10］ Wang J，Zabaras N.Hierarchical Baysesian models for inverse problems in heat conduction Issue［J］.Inverse Problem，2005，21（1）：183-206.

［11］ Wang J，N Zabaras.Using Bayesian statistics in the estimation of heat source in radiation Int［J］.Heat Mass transfer，2005，48：1529-1542.

［12］ 童景山.流体热物性学-基本理论与计算［M］.北京：中国石化出版社，2008.

［13］ Lee J，Jung S Y，Sung H J，et al.Turbulent thermal boundary layers with temperature-dependent viscosity［J］.Int Jof Heat and Fluid Flow，2014.

［14］153 毛宇飞，白博峰，郭烈锦.混合长度理论的改进及其在变物性传热中的应用［J］.工程热物理学报，2011，32（1）：58-62.

［15］ 陶文铨.数值传热学［M］.西安：西安交通大学出版社，2009.

［16］ Tarantola A.Inverse Problem Theory and Methods for Model Parameter Estimation［M］.Pennsylvania：SIAM，2005.

A Research on ldentifying Thermophysical Parameter of Pipe Turbulence Fluid by lnverse Heat Transfer Problem

MEI Ning，JIAO Si
（College of Engineering，Ocean University of China，Qingdao 266100，China）

A method to identify the thermophysical parameters by measuring the pipe convection heat transfer temperature field was presented in this paper.The governing equations for turbulent forced convection heat transfer in pipe were simplified according to the boundary-layer theory.and an improved mixing length turbulence model was developed by introducing the effect of density fluctuations into the equations of turbulent transport，which can be applied to calculate the temperature field and velocity field inside the pipe.Using Levenberg-Marquardt method got the viscosity coefficient in the control equations by measured temperature field.The results show that IHTPis feasible for identifying the thermophysical parameters and has a higher precision.

Levenberg-Marquardt method；mixing length turbulent model；turbulent convective heat transfer；turbulent viscosity coefficient

TK124

A

1672-5174（2014）10-142-06

责任编辑 陈呈超

国家自然科学基金项目（51276174）；青岛市科技发展计划项目（12-1-3-77）资助

2014-06-20；

2014-08-20

梅 宁（1961-），男，教授，博导。E-mail：nmei＠ouc.edu.cn