基于Archimedean Copula函数的风浪联合统计分析❋
董 胜,翟金金,陶山山
(中国海洋大学工程学院,山东青岛266100)
基于Archimedean Copula函数的风浪联合统计分析❋
董 胜,翟金金,陶山山
(中国海洋大学工程学院,山东青岛266100)
选取渤海海域某导管架平台24年的年最大波高和相应风速,基于Gumbel分布对2个边缘分布的拟合优度检验,采用Archimedean Copula函数族中的4种函数构建两变量联合概率分布模型,并进行了拟合优度评价。利用优选出的Clayton Copula函数,计算风浪联合分布的联合重现值。以海洋平台响应作为约束条件,进行了二维Clayton Copula函数的风浪联合统计分析。研究结果表明:基于Copula函数构造的二维分布,考虑了风浪之间的相关性,在相同重现值设计参数下,可以降低导管架平台的结构响应,从而可以降低海洋平台的环境条件设计标准。
年极值波高;相应风速;边缘分布;联合分布;Archimedean Copula
风浪主要是指在风直接作用下产生的波浪[1],它的形成与风速有着密切的关系。风浪具有巨大能量,对海岸或海洋建筑物产生巨大的冲击力,从而威胁海洋建筑物的安全。因此,深入分析波高和风速的联合概率分布对海洋工程的安全防护以及风险控制都十分重要。
目前,已经有一些多变量联合概率分布应用于海洋水文环境要素的研究。例如,段忠东基于多变量极值理论建立了风速和有效波高的联合概率分布[2]。周道成和段忠东采用Gumbel逻辑模型描述了年极值风速和有效波高的联合分布[3]。Yue等将二维Gumbel分布用于水文的概率分析中[4]。董胜等采用泊松二维逻辑分布[5]、二维皮尔逊Ⅲ型联合分布[6]和二维逻辑Gumbel分布[7]分别对极值风速与波高的联合概率分布、年极值有效波高与风速的联合概率分布和波高与风速的联合重现期进行了分析计算。Dong等采用二维对数正态分布模拟了风浪的联合重现期[8]。但这些传统的多变量频率分析模型都要求各变量服从相同类型的边缘分布,从而限制了其适用范围。Copula函数的出现解决了这类问题,它不要求变量的边缘分布必须为同一类型的分布,因而可以构造任意边缘分布组合的联合分布;同时能够把边缘分布和变量间的相依关系分开考虑,从而可以选择拟合更优的边缘分布,具有极强的灵活性和适应性,是描述随机变量间相关性的一种重要工具。
Copula函数虽早在1959年已被Sklar[9]提出,至1990年代才得以迅速发展,目前仍处于发展阶段。Copula函数最初被应用于金融、保险、生物建模等领域,近年来Copula函数在海岸与海洋工程的联合概率分布分析中得到了越来越广泛的应用。Wist等利用二元正态Copula函数建立了波高和波周期的联合分布,并成功应用于日本海域的海洋工程[10]。秦振江等利用Copula函数建立了最大有效波高和最大风速的联合概率分布,并进行了模型检验,结果表明Copula函数能够较好地模拟实际的数据[11]。董胜等基于Clayton Copula函数建立了年最大波高和风速的二维联合分布模型,并将其应用在海洋平台环境荷载的联合设计中,合理降低了荷载设计参数,从而减少海洋工程的投资[12]。陈子燊基于4种Archimedean Copula函数建立极值波高与相应风速的联合概率分布模型,并与单变量分布进行比较分析,研究表明,两变量联合分布比单变量分布更能全面地反映极端海况条件下的重现水平[13]。Tao等基于二维Gaussian Copula函数和Frank Copula函数分别建立波高和风速的联合概率分布,从而为海洋工程设计提供安全可靠的设计参数[14]。徐龙军等将基于Archimedean Copula函数C-测度的第二重现期应用于风浪联合分布的重现期分析中,经实际数据验证,此方法的计算结果更接近荷载效应实际重现期[15]。Yang和Zhang在渤海区域风浪后报的基础上,基于Copula函数建立了波高和风速的联合分布,并进行了频率分析[16]。上述研究成果反映了Copula函数是一个相对简单、灵活的联合分布模型,可以较好地模拟海洋工程极值事件,为确定海洋工程环境设计参数提供了一种新方法。
本文采用Archimedean Copula函数开展渤海海域风浪联合概率分析的研究。第一部分简要介绍Archimedean Copula函数的定义和几种常用的Archimedean Copula函数;第二部分采用Archimedean Copula函数构建年最大波高和相应风速的联合分布函数;第三部分进行拟合优度的评价,选择最优的Copula函数建立联合分布模型;第四部分对渤海海域某导管架平台的年最大波高与相应风速进行风浪联合分布的联合重现值计算,并通过海洋平台的响应计算,进行二维Clayton Copula函数的风浪联合统计计算,得出结论。
1 Archimedean Copula函数
二维Archimedean Copula函数可以定义为
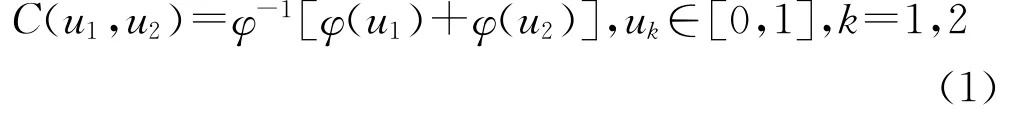
式中:φ(·)称为Archimedean Copula的生成元,φ(·)是[0,1]→[0,∞]的连续严格递减函数,且φ(1)=0,φ(0)=∞;φ-1为φ的逆函数,其在[0,+∞]上单调,除了φ-1(0)=1和φ-1(∞)=0外,有

Archimedean Copula由其生成元确定的单参数函数,是目前运用较为广泛的一类Copula函数。其中,海洋工程领域中最常用的二维Archimedean Copula主要有以下几种:
(1)Clayton Copula:

(2)Frank Copula:

(3)Ali-Mikhail-Haq(AMH)Copula:

式中:C(·,·)为二维Copula的分布函数;u1和u2分别表示边缘分布函数,即u1=F1(x1),u2=F2(x2);θ为Copula函数的参数。
2 边缘分布函数
2.1边缘分布函数选取
采用不同的概率分布对单变量样本进行拟合时,其设计重现值会有较大差别,而Gumbel分布拟合时较为保守,为了保证结构安全,本文年最大波高和相应风速的边缘分布均选取Gumbel分布。Gumbel分布又称极值Ⅰ型分布,首先由Fisher导出,E J Gumbel于1941年应用在水文洪水频率分析中。Gumbel分布的基本理论是已知随机变量的原始分布为指数型分布,在同一条件下做多次试验,得到n组随机变量,取各组的极大值或最小值(称为极值)组成极值系列,此极值分布渐近于Gumbel分布[17]。其分布函数为

其密度函数为

式中:α为尺度参数;μ为位置参数。该分布函数与其概率的关系为

而概率P与重现期T的关系为

联立式(7)、(9)、(10),可得
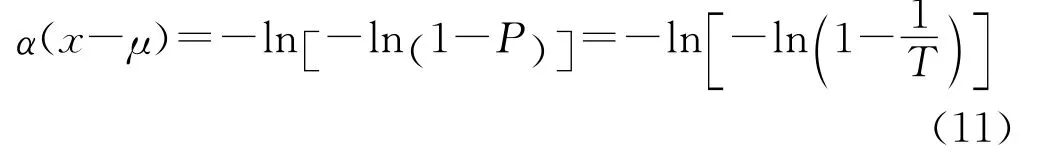
根据式(11)和观测序列进行拟合可求得Gumbel分布的参数α和μ。重现期为T的风浪极值为

2.2边缘分布拟合检验
由样本判断总体分布类型,这种检验称为拟合优度检验,也称分布拟合检验。常用的检验方法有:χ2检验、Kolmogorov-Smirnov(K-S)检验、Cramer-von Mises(C-M)检验、Aderson-Darling(A-D)检验、修正Watson检验和Liao-Shimokawa检验等。
本文采用K-S检验,设总体X的分布函数为F(x),F0(x)为已知理论分布。令原假设:H0:F(x)=;备选假设:H1: F(x)≠F (x)。采用K-S检验,选取统计量D:
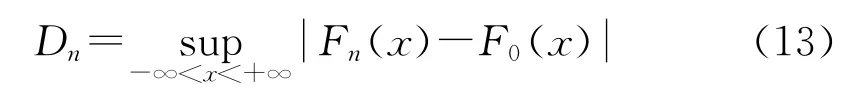
式中:Fn(x)为经验概率分布函数。令

则统计量Dn的观测值为

取显著水平α=0.05,对不同的样本容量n,通过查表可得K-S检验的临界值Dn(0.05)。如果^Dn<Dn(0.05),则不拒绝原假设H0,也即认为样本所得的概率分布符合参数为α与μ的Gumbel分布;否则拒绝原假设H0,也即认为样本所得的概率分布不符合参数为α与μ的Gumbel分布。
3 Copula函数参数估计与拟合优度评价
3.1 Copula函数参数估计
Copula函数的参数估计方法主要有极大似然法[18-19]、边际函数推断法[19]、非参数核密度估计[20]、矩估计法[21]、相关性指标法[22]等。其中,相关性指标法主要是根据Kendall秩相关系数τ与Copula函数的参数θ的关系(见表1)来计算参数θ。

表1 对称Archimedean Copula函数的τ与θ的关系Table 1 Relation ofτandθin symmetric Archimedean Copula function
3.2 Copula函数拟合优度评价
Copula函数的拟合优度评价是选择Copula模型的重要原则。常用的评价方法有:直观的图形分析法、均方根误差法(RMSE)、AIC信息准则法、BIC信息准则。
(1)直观的图形分析法
该方法将经验联合概率值点和理论联合概率值绘成散点图,如果点距较均匀地分布在45°线附近,则说明建立的联合概率分布模型是合理的。此方法可以直观描述拟合的优劣程度。
(2)均方根误差法(RMSE)
式中:n为样本容量;Pc为Copula多元联合分布理论频率值;P0为多元联合分布经验频率值,计算公式为

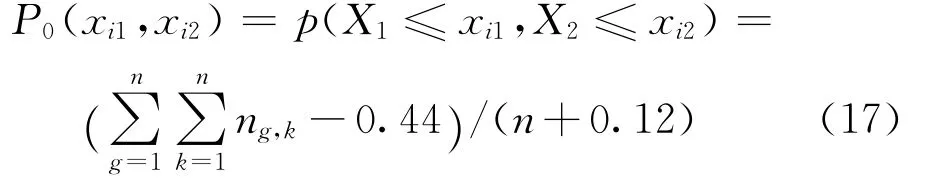
式中,ng,k为同时满足X1≤xi1,X2≤xi2的联合观测数值个数。RMSE值越小,Copula函数拟合的效果越好。(3)AIC信息准则法
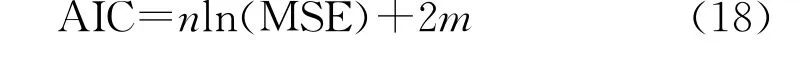
m为Copula参数估算数。AIC值越小,Copula函数拟合的效果越好。
(4)BIC信息准则法
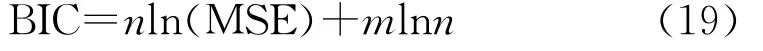
式中参数同上,BIC值越小,Copula函数拟合的效果越好。
4 工程实例
4.1算例数据
本文选取渤海海域某导管架平台1970—1993年年最大波高和相应风速(见图1)的观测值,并根据该二维统计序列进行研究。

图1 数据散点图Fig.1 Scatter plot
4.2边缘分布函数参数及分布拟合检验
采用Gumbel分布作为年最大波高和相应风速的单变量边缘分布,根据式(11)利用最小二乘法求Gumbel分布的参数。计算得年最大波高的尺度参数和位置参数分别为α=1.886 0、μ=2.814 0;相应风速的尺度参数和位置参数分别为α=0.382 1、μ=14.521 6。
通过计算,年最大波高及其相应风速的K-S统计量分别为DH=0.102 3,DV=0.120 5,均小于显著水平D24(0.05)=0.27,从而说明都符合Gumbel分布,其拟合结果见图2。

图2 单变量边缘分布拟合Fig.2 Marginal distribution of statistical variables
4.3 Copula函数参数的确定
根据相关系数指标法,可以求得4种Archimedean Copula函数的参数值(见表2)。

表2 4种Copula函数参数估计值Table 2 Parameter estimated values of 4 kinds of Copula functions
4.4 Copula函数的选取
将4种Copula函数计算得到的理论联合概率分布和经验联合联合概率分别点绘在图中(见图3)。从图中可以看出,数据点均分布在45°直线附近,可以直观的看出4种Copula函数拟合效果都比较好。
为了获得最优的拟合分布函数,根据拟合优度评价指标,计算RMSE值和AIC值(见表3),选取两样本中RMSE和AIC最小的Clayton Copula函数作为联合概率分布的连接函数。
4.5联合概率分布与重现水平
根据Clayton Copula函数建立年最大波高和相应风速的联合分布。年最大波高和相应风速的联合概率分布和联合概率等值线见图4。图中标注的0.02、0.01和0.005等曲线分别表示波高和相应风速联合重现期分别为50、100和200年的等值线。具体计算结果见表4,表4中波高和风速独立时,重现期为各自的重现期;在波高主极值条件下,重现期是波高的重现期;其它的情况下表示风浪的联合重现期。
由表4可见,单变量计算的200年一遇的波高和风速共同发生的概率仅为0.004%,为25 000年一遇;100年一遇的波高和风速共同发生的概率为0.02%,为5 000年一遇;25年一遇的波高和风速共同发生的概率为0.27%,为370年一遇。在波高主极值条件下,基于两变量联合分布计算得到的风速设计值小于单变量计算得到的风速设计值,并且差值随着重现期的增大而增大,重现期10~200年的风速设计值相对单变量计算得到的设计值减小15.61%~43.80%。在风浪联合概率密度最大的条件下,基于两变量联合分布计算得到的波高和风速均小于单变量计算得到的波高和风速设计值。可以看到联合概率分析极大地降低了环境要素的设计值。
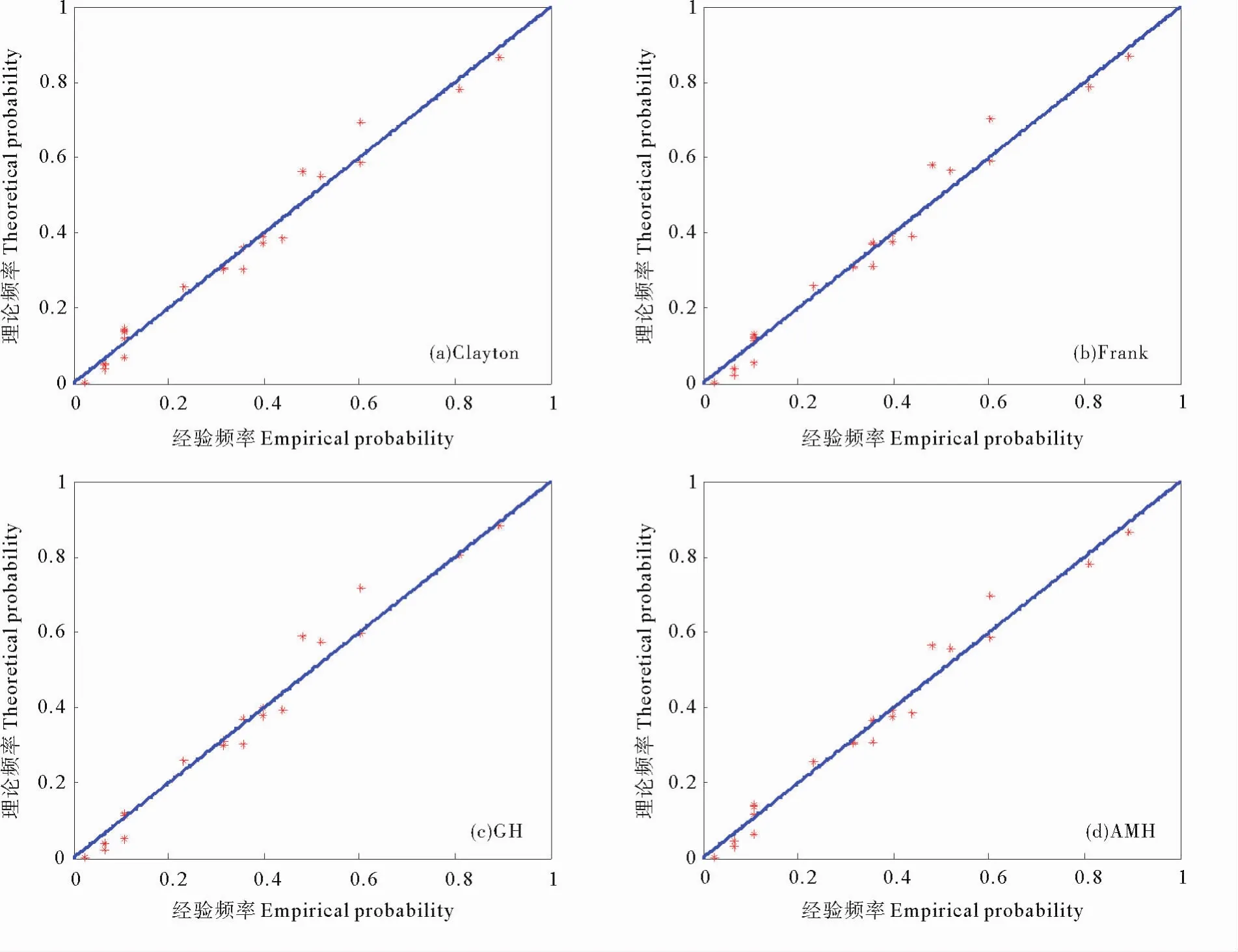
图3 经验联合概率与Copula理论联合概率分布的拟合Fig.3 Empirical probability and Copula joint probability distribution
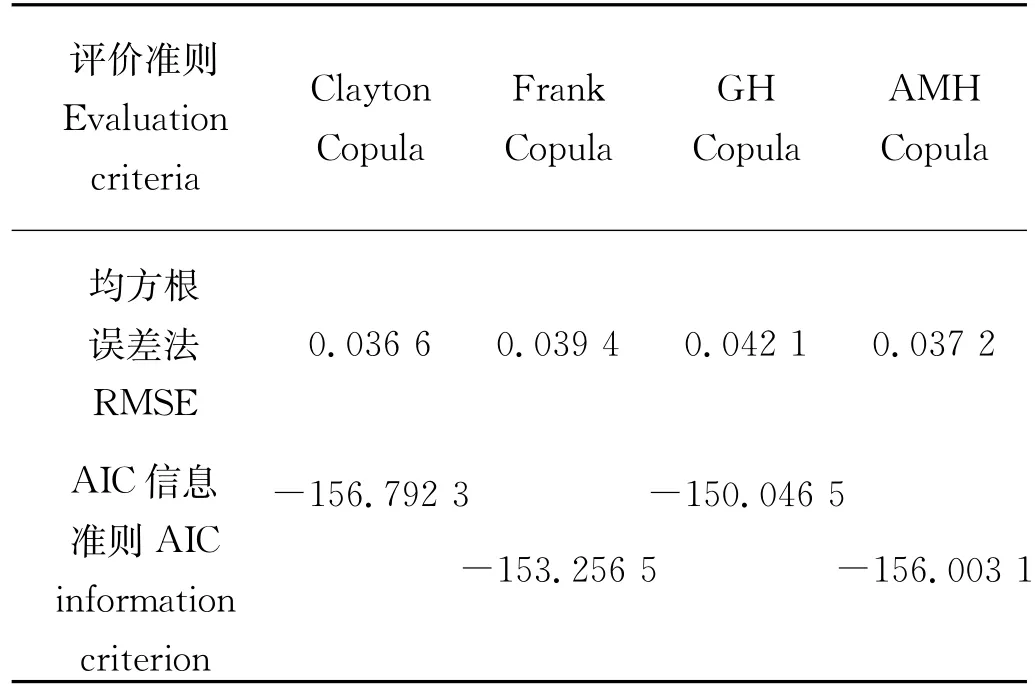
表3 年最大波高及其相应风速联合概率分布函数的拟合优度评价Table 3 Priority degree evaluation of joint distribution of maximum wave height and corresponding wind speed

图4 年最大波高和相应风速的联合分布图Fig.4 Joint probability distribution of maximum wave height and corresponding wind speed
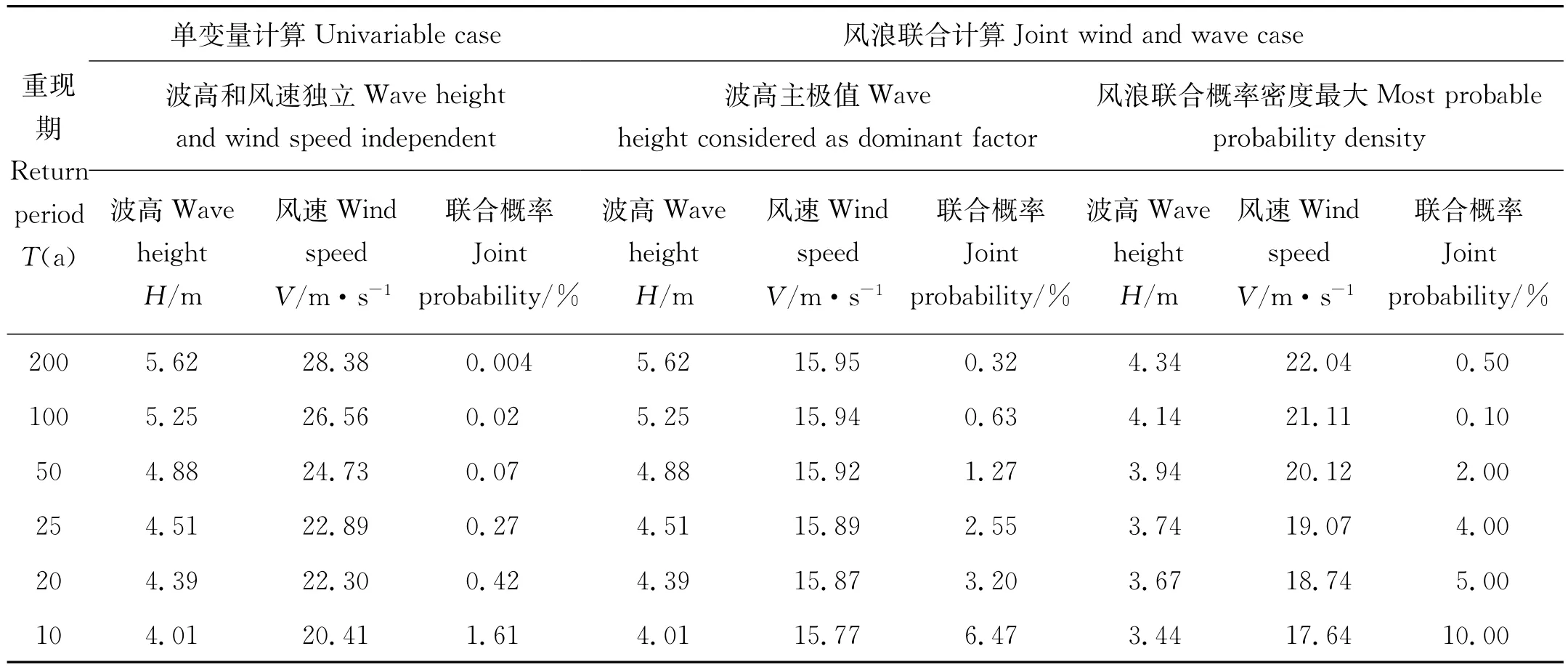
表4 年最大波高和相应风速的不同重现期下的设计值Table 4 Different return design values under joint maximum wave height and corresponding wind speed
4.6风浪联合统计在海洋工程中的应用
此海域的导管架平台的基底剪力Q、倾覆力矩M和甲板的最大位移D分别按式(20)、(21)和(22)计算[23]:
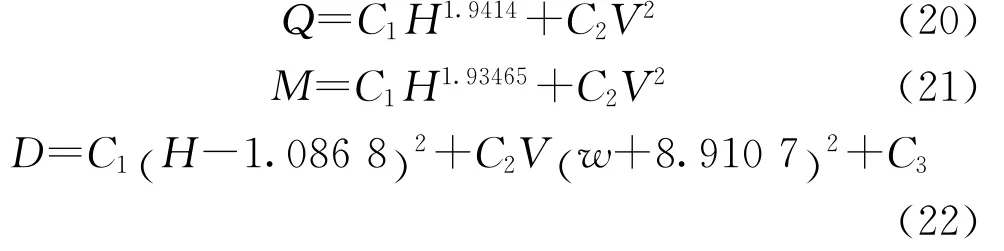
式中:H和V分别表示波高和风速;C1、C2和C3对具体的导管架平台近似为常数,式(20)取C1=20.379 7和C2=0.115 3;式(21)取C1=234.249 1和C2= 0.290 8;式(22)取C1=0.000 1、C2=1.387 9×10-6和 C3=0.008 7。
式(20)、(21)、(22)计算得到的基底剪力、倾覆力矩和最大位移见图5中的虚线,每条重现期的响应值对应着相应的波高和风速。图中的切点表示该重现水平下海洋平台响应最大时所对应的波高和风速的组合,计算结果见表5。表5中波高和风速独立时,重现期为各自的重现期;在波高主极值条件下,重现期是波高的重现期;其它的情况下表示风浪的联合重现期。此外,将表4中所得波高和风速独立、波高主极值和风浪联合概率密度最大时3种条件下的波高和风速分别代入式(20)、(21)、(22),计算结果亦见表5。

图5 响应等值线Fig.5 Response contours
从图5(a)中可以看出,100年一遇的基底剪力所对应的波高和风速分别为5.24 m和12.32 m/s,比表4中单变量计算得到的100年一遇的波高和风速分别减小0.19%和53.61%;从(b)中可以看出,100年一遇的倾覆力矩所对应的波高和风速分别为5.25 m和12.18 m/s,比表4中单变量计算得到的100年一遇的波高和风速分别减小0%和54.14%;从(c)中可以看出,100年一遇的最大位移所对应的波高和风速分别为5.14 m和14.67 m/s,比表4中单变量计算得到的100年一遇的波高和风速分别减小2.10%和44.77%。
从表5能够看到各重现期下的基底剪力、倾覆力矩和甲板的最大位移通过联合概率计算均降低了。100年一遇的基底剪力在波高主极值、联合概率密度最大、基底剪力最大、倾覆力矩最大和最大位移最大的5种不同的联合条件下均小于波高和风速独立下的基底剪力,降低8.8%~37.0%。100年一遇的倾覆力矩在5种不同联合条件下均小于波高和风速独立下的倾覆力矩,降低5.5%~28.2%。100年一遇的最大位移在五种不同的联合条件下均小于波高和风速独立下的最大位移,降低7.4%~10.7%。而设计参数的降低将导致海洋结构设计成本的下降。

表5 给定重现期时的响应设计值Table 5 Design values of response under given return periods
5 结论
以渤海海域某导管架平台24年的年最大波高和相应的风速为研究实例,基于Gumbel边缘分布,构造了4种二维Archimedean Copula函数的联合分布模型:Clayton Copula,Frank Copula,GH Copula和AMH Copula。通过计算得到以下结论:(1)通过拟合优度的评价,得到Clayton Copula函数拟合年最大波高及其相应风速的效果最好,故选用Clayton Copula计算渤海海域的风浪联合分布;(2)在波高主极值、联合概率密度最大、基底剪力最大、倾覆力矩最大和最大位移最大5种不同的条件下,Clayton Copula联合分布计算的波高和风速的设计值均小于单变量计算的设计值;同时,在给定重现期下,基底剪力、倾覆力矩和甲板的最大位移通过联合概率计算均比波高和风速独立条件下降低了。从而可见,Copula联合分布能够有效合理地降低海洋工程的环境荷载设计标准,从而减少工程投资。
[1] 董胜,孔令双.海洋工程环境概论[M].青岛:中国海洋大学出版社,2005.
[2] 段忠东,周道成,肖仪清,等.极值风浪联合概率模型参数估计的简化方法[J].哈尔滨建筑大学学报,2002,35(6):1-5.
[3] 周道成,段忠东.耿贝尔逻辑模型在极值风速和有效波高联合概率分布中的应用[J].海洋工程,2003,21(2):45-51.
[4] Yue S.The Gumbel logistic model for representing a multivariate storm event[J].Advances in Water Resources,2001,24(2):179-185.
[5] 董胜,郝小丽,樊敦秋.海洋工程设计风速与波高的联合分布[J].海洋学报,2005,27(3):85-89.
[6] 董胜,丛锦松,余海静.涠洲岛海域年极值风浪联合设计参数估计[J].中国海洋大学学报:自然科学版,2006,36(3):489-493.
[7] 董胜,林雪,陶山山,等.基于危险率分析的风浪联合重现期研究[J].中国海洋大学学报:自然科学版,2012,42(3):80-84.
[8] Dong S,Liu Y K,Wei Y.Combined return values estimation ofwind speed and wave height with Poisson Bi-variable Lognormal distribution[C].Seoul:The Proceedings of 15th International Offshore and Polar Engineering Conference,2005,3:435-439.
[9] Sklar A.Fonctions de repartitionàn dimensions et leurs marges[J].Publ Inst Statist Univ Paris,1959,8:229-231.
[10] Wist H T,Myrhaug D,Rue H.Statistical properties of successive wave heights and successive wave periods[J].Applied Ocean Research,2005,26(3-4):114-136.
[11] 秦振江,孙广华,闫同新,等.基于Copula函数的联合概率法在海洋工程中的应用[J].海洋预报,2007,24(2):83-90.
[12] 董胜,周冲,陶山山,等.基于Clayton Copula函数的二维Gumbel模型及其在海洋平台设计中的应用[J].中国海洋大学学报:自然科学版,2011,41(10):117-120.
[13] 陈子燊.波高与风速联合概率分布[J].海洋通报,2011,30(2):158-163.
[14] Tao SS,Dong S,Xu Y-H.Design parameter estimation of wave height and wind speed with bivariate Copulas[C].∥The Proceedings of the 32nd International Conference on Ocean,Offshore and Arctic Engineering.Nantes:ASME,2013.
[15] 徐龙军,陈祉宏,周道成,等.基于Archimedean Copula模型的风浪联合分布第二重现期[J].天津大学学报,2013,46(2):114-120.
[16] Yang X C,Zhang Q H.Joint probability distribution of winds and waves from wave simulation of 20 years(1989-2008)in Bohai Bay[J].Water Science and Engineering,2013,6(3):296-307.
[17] 邱大洪.工程水文学[M].北京:人民交通出版社,2011.
[18] 邱小霞,刘次华,吴娟.Copula函数中参数极大似然估计的性质[J].经济数学,2008,25(2):210-215.
[19] 杨益党,罗羡华.Copula函数的参数估计[J].新疆师范大学学报:自然科学版,2007,26(2):15-18.
[20] 赵丽琴,籍艳丽.Copula函数的非参数核密度估计[J].理论新探,2009(9):29-32.
[21] 刘俊涛,陈希镇.Copula函数中参数的矩估计[J].科学技术与工程,2009,9(21):6460-6464.
[22] 杜江,陈希镇,于波.Archimedean Copula函的参数估计[J].科学技术与程,2009,9(3):637-640.
[23] 徐英辉,董胜,陶山山.渤海导管架平台结构响应计算公式拟合[J].海洋湖沼通报,2013(4):173-180.
Joint Statistical Analysis of Winds and Waves Based on Archimedean Copula Function
DONG Sheng,ZHAI Jin-Jin,TAO Shan-Shan
(College of Engineering,Ocean University of China,Qingdao 266100,China)
Four kinds of common-used Archimedean Copulas(Clayton,Frank,GH,AMH)were applied to construct joint probability distribution of annual extreme wave height and corresponding wind speed,meanwhile the two margins are both taken as Gumbel distribution.These joint models could make the best use of marginal information and the correlation between the two radon variables.Observations about wave height and wind speed on a jacket platform in Bohai Sea were applied to verify the efficiency of these joint models.Based on goodness-of-fit,Clayton model was the optimal selection for this data to calculate joint return values.Considering constraint conditions of offshore platform responses,two-dimensional Clayton Copula was used to analyze joint statistical characters of winds and waves. The result shows that the two-dimensional joint distribution based on Copula considers correlation between waves and winds;meanwhile the offshore platform responses and the loads design criterion can be lowered by the joint distribution comparing with univariate method.
annual maximum wave height;corresponding wind speed;marginal distribution;joint distribution;Archimedean Copula
TE951
A
1672-5174(2014)10-134-08
责任编辑 陈呈超
国家自然科学基金项目(51279186;51479183);国家留学基金项目(201406335003);中央高校基本科研业务费专项(201413003)资助
2014-07-10;
2014-09-10
董 胜(1968-),男,教授,博导。E-mail:dongsh@ouc.edu.cn

