激光外差干涉仪相位计的设计

乐燕芬，李霄夏，句爱松

激光外差干涉仪相位计的设计

乐燕芬，李霄夏，句爱松

（上海理工大学光电信息与计算机工程学院，上海200093）

外差信号的比相处理是决定外差干涉仪精度、分辨率等性能的重要因素。为了解决比相计的分辨率和检测速度之间的矛盾，采用比相方法进行了测量原理、应用特点及局限性的理论分析，给出了相应的解决方案。结果表明，基于现场可编程门阵列的整周期采样可以提高自相关方法的测量精度，混频过零检测方法可以提高测量速度。

测量与计量；外差干涉；比相计；相位测量

引 言

激光外差干涉是在干涉测量的基础上，于20世纪60年代开始提出。由于干涉时使测量光与参考光产生一个微小频率差Δω，使得干涉信号成为频率为Δω的正弦信号。通过检测不同点此正弦信号的相位即可测得物体表面的形状、位置偏移等。由于其测量分辨率高、准确度高及非接触等特点，使激光外差技术在需要高精度检测的微加工、微制造领域获得了广泛的应用。

激光外差的高精度测量主要取决于两个因素：（1）外差干涉系统光路的设计；（2）比相计的相位检测精度。在完成光学系统设计后，比相计的精度决定了系统的测量精度。随着工业制造加工领域对检测速度和检测精度要求的不断提高，如何在高速实时测量的同时，实现高精度相位测量成为设计外差干涉相位计面临的新挑战。本文中对近年来常用的相位计设计方法进行了介绍并分析其设计要点。

1 外差干涉

图1是典型的用于位移测量的外差干涉系统原理图［1］。

外差干涉系统主要由激光器、包含测量臂和参考臂的干涉系统以及相位计组成。由激光源提供的光束包含两束偏振方向正交且具有一定频差的线偏振光分量。经分光镜分束后，一束成为参考光，另一束成为测量光。测量光中的两个正交的线性偏振光束经过偏振分光镜后分开，其中一个频率分量f1沿测量臂到达测量镜并反射，与从参考镜返回的另一频率分量f2汇合，经检偏器后成为测量信号。这类光源一般采用塞曼分裂的He-Ne激光器，两个线偏振光分量频差较大，在1.8MHz～20MHz左右。还有一种是稳频单模He-Ne激光器加上光学频移器件，目前主要是声光调制器，也可产生两个线性偏振分量，频差在几千至几兆赫兹范围内可调，但增加了系统的复杂度。

图1 外差干涉原理图

图1中，当测量镜沿运动光轴有相对运动速率v（t）时，从测量镜返回的f2光束产生多普勒频移Δf，并可用下式表示： Δf＝2v（t）／λ（1）式中，λ是光束的波长。在信号处理的Δt时间内，经积分可获得测量镜的运动位移ΔL：

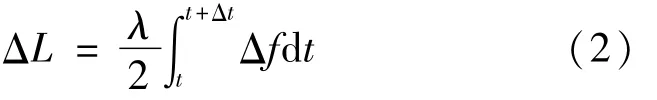
同时也可知，测量镜的运动位移引起测量信号相位变化Δφ，并可表示为： Δφ＝4πΔL／λ（3）

再结合图1所示的外差干涉原理图，则系统的参考信号Ir和测量信号Im可分别表示为：

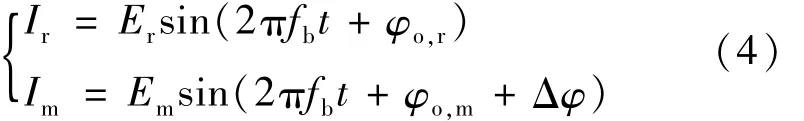
式中，Er，Em分别是参考信号和测量信号的幅值；fb＝f1－f2，为检偏器获取的拍频信号频率；φo，r和φo，m为参考信号和测量信号的初始相位；Δφ对应测量臂光程变化量而引入的相移，通过检测该相位变化量Δφ，可获得被测物的实时位移大小。

由（1）式可知，被测物运动速率与多普勒频移之间为线性关系。并且当测量镜运动速率为1m／s时，产生的多普勒频移Δf可达3.16MHz。研究表明［1］，多普勒频移Δf与干涉系统的拍频fb满足下式关系时，被测件快速运动中不丢失对整周期相位差（2π的整数倍）的检测： Δf＜2fb／3（5）

这样，结合（1）式可知，若要检测运动速率达1m／s的被测物，干涉系统的拍频需达4.74MHz。一般比相计设计中参考信号均采用该拍频信号，这也意味着系统拍频fb限制了比相计的检测带宽Δf，进一步也限制了测量速率。

而（3）式表明，测量分辨率取决于相位计的比相精度。对于He-Ne激光器（波长633nm），如果位移的测量分辨率要达到0.9nm，则相位计的比相精度需达1°。如果要达到亚纳米级的测量精度，或者着眼于提高干涉系统的光学倍程数，从二倍频到四倍频，甚至更高；或者提高相位计的比相精度。

图2中给出了目前商用比相计基于“过零检测”的比相原理［1-2］。测量信号与参考信号的相位比较转换为两个信号的时间差ΔT比较。由图2可知： Δφ＝360°ΔT／Tr＝360°frNΔτ（6）式中，Tr，fr分别是参考信号的周期和频率，Δτ是高频脉冲的周期，N是ΔT时间内的高频脉冲个数。比相计的检测分辨率取决于高频脉冲与参考信号的频率比值。在一般设计中参考信号的频率即为拍频，也即fr＝fb。因此，要实现高精度的相位测量，要求高频脉冲具有极高的时间分辨率，这对目前的电子电路提出了相当高的要求。或者可考虑降低参考信号的频率，则在一定的相位测量分辨率下，对高频脉冲的时间分辨率要求就降低了。

图2 比相的基本原理

综合上述分析可知，对比相计的性能而言，要求检测速度快，则要求参考信号频率尽可能高；而要提高检测分辨率，则参考信号的频率越低越容易实现。两者相互矛盾。比相计的设计要综合考虑两者因素，参考文献［3］中设计的比相计就采用对应20MHz和2.0kHz两个拍频的两种工作模式来达到满足实际应用的最优设计。

2 常见的比相方法

当光学系统确定，外差干涉的信号处理电路决定了干涉仪的测量精度和测量分辨率。干涉仪比相计的设计原则上要求在保证检测速率的同时，达到尽可能高的分辨率。比相计接收并处理的信号形式如（4）式所示。需特别注意的是：干涉测量是个动态过程，相位差Δφ动态变化，因此相位的测量需保证一定的实时性；同时在不同测量应用下，被测物运动速率可快可慢，故需考虑测量信号频率fb±Δf的动态变化范围。

目前常用的干涉信号处理方式有如下几种。

2.1基于数字相关的相位差测量

对于信号x（t）和y（t），相关运算定义如下：

式中，T为信号周期。在相关运算中，同频率信号具有相关性，而噪声与信号无关，因此利用相关运算求相位，对模数转换量化及采样的噪声不敏感，具有很强的噪声抑制能力。

如果对干涉信号做相关运算可得：

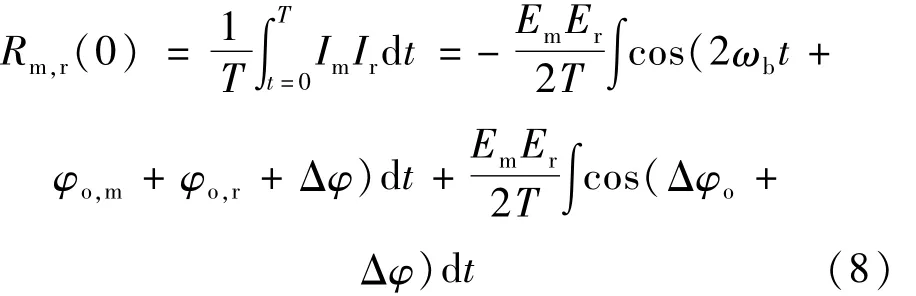
式中，ωb＝2πfb，为角频率；Δφo＝φo，r－φo，m，为初始相位差。具体实现时，一般都是对干涉信号进行模数转化后再做数字相关运算。因此要保证对测量信号的整周期采样，也即采样频率fs＝N·fb，（8）式中的第1项积分才为0。则可得：

假设测量周期内（也可以是M个Tb）相位差保持不变，则：

上式表明，通过单相关运算可获得相位差信息。但此方法中涉及测量和参考信号的幅值，因此干涉系统中所有可能影响光强变化的因素，包括环境噪声、激光源光强漂移等都会影响测量精度。因此在此基础上提出双相关的测量方法。

假设可获得参考信号的正交信号为Ir′＝Er× cos（ωbt+φo，r），则对测量信号与该正交参考信号做相关运算，可得：

故有tan（Δφo+Δφ）＝Rm，r′／Rm，r。因为干涉测量是一种增量式测量，系统的初始相位差Δφo确定，则其影响的只是零点偏置量或者干涉仪静态时的初始相位。通过零点重置可消除其影响。因此相位测量公式也可表示为：

由（12）式可知，数字双相关法进行相位测量对参考信号与测量信号的幅值不敏感，可避免光功率漂移引入的信号误差。在对离散取样的参考信号和测量信号完成相关运算后，利用反正切运算即可获得干涉位移变化引起的相位差。

常用的反正切算法包括泰勒级数法、查表法以及坐标旋转数字计算（coordinate rotation digital computing，CORDIC）算法。考虑实时性及角度分辨率，可采用适合在高速现场可编程门阵列（filed-programmable gate array，FPGA）实现的CORDIC算法。采用流水线结构的CORDIC算法可在1个时钟周期（即系统时钟，或者采样数据的时钟fs）获得比相输出。对于100MHz的系统时钟，采用12级流水线，CORDIC算法可在10ns内实时得到相位分辨率达0.02°的比相输出［4-5］。

数字相关法应用于干涉仪的相位测量，需解决的问题主要有以下两点。

（1）如何实现干涉信号的整周期采样。利用FPGA，作者提出一种实现方案。如图3所示。

图3 基于FPGA的整周期采样实现

此方案利用FPGA所带的锁相环模块，对整形后的参考信号进行倍频得到采样时钟fs，该时钟信号作为整个信号处理电路的基准信号。倍频率可根据精度要求、参考信号的频率、FPGA的时钟频率选择6～12。由于采用干涉系统的参考信号作为锁相环倍频源，因此该方案具有很好的动态适应性，且对激光源提供的干涉拍频信号频率的漂移不敏感。

但当被测件快速运动测量时，产生的多普勒频移较大。采用上述方案可跟踪参考信号频率而实现整周期采用，但对测量信号此时无法实现整周期采用，必然会引入误差［6］。此误差的大小则需根据实际应用进行测算，保证其在允许范围内。因此相关干涉法适合精度高、拍频低（不高于20MHz）、测量速率较低的应用。

（2）如何生成幅值相同、90°相移的正交参考信号。这是双相关法测量相位差的首要条件。生成方法可考虑光学实现或电信号实现。在光学系统中，通过插入λ／4波片可实现相位超前或滞后90°或者利用渥拉斯顿棱镜获得正交相位的参考信号［7］。但不管哪种方法，每路正交参考信号的获取都需要独立的光电接收器，这就很难保证幅值相等；另外只有光程完全一致，两路参考信号才能保证正交，否则都会引入额外的相差。电信号的实现则是基于模数转换后存储的离散参考信号。因为拍频已知，通过数据寻址地址增加或减少1／4周期即可获得正交信号的离散值。此方法实现容易，但因为激光源提供的干涉拍频信号频率有一定的漂移范围，因此该方法会引入一定的误差。

2.2基于数字I／Q的相位测量

数字同相正交调制（in-phase／quadrature，I／Q）技术进行鉴相的核心是提供一对正交本振信号，频率为拍频或接近拍频。测量信号与参考信号分别与该本振信号绝对鉴相，进而获得测量信号与参考信号的相位差。

绝对鉴相原理如图4所示。

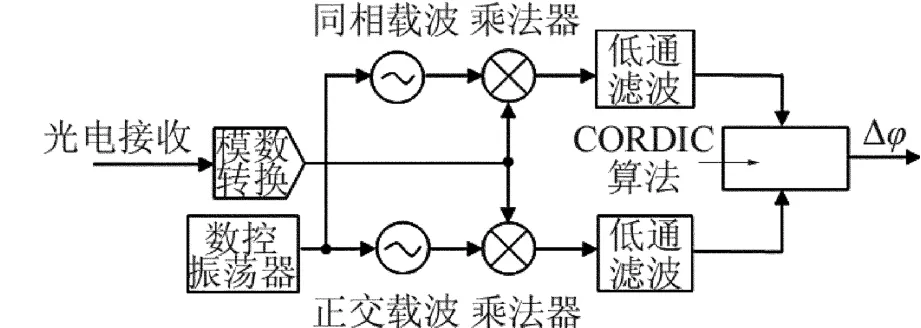
图4 基于数字I／Q技术的数字鉴相原理框图

光电接收器接收的参考信号／测量信号，与本地正交振荡信号相乘，经低通滤波器后得基带信号，该基带信号包含参考／测量信号与本地振荡信号的绝对相位差。通过比较两路信号的绝对相位差，可得测量信号与参考信号之间的相对相位差［8-9］。此办法对信号幅值变化不敏感。因此测量环境变化、激光源偏移等引起的光强变化不会影响测量结果，测量精度较高。比相计的相位分辨率主要由数控振荡器的相位增量和CORDIC模块的级数决定。

应用此方法需要解决的主要问题有：（1）整周期采样。这是涉及模数转换的比相计共同面临的难题，采用第2.1节中提出的参考信号或测量信号倍频后作为采样时钟，在高精度低速测量应用中可解决该问题；（2）低通滤波器的合理设计。低通滤波器需要滤除的高频信号是2fb±Δf，保留基频信号Δf，当被测件高速运动时，Δf接近fb，则这两个频率很难区分，因此滤波器截止频率的设计限制了比相计的测量带宽。这个问题同样存在于参考文献［1］中。另外，滤波器的设计要避免引入额外的相位变化。采用零相位滤波可以解决这个问题［6］，但信号处理的时间延长，实时性受到影响。

2.3基于过零检测填脉冲式的相位测量

这类方法的基本原理如图2所示，比较测量信号与参考信号的过零时间点，并由此获得相位差。在具体实现时，常用高频脉冲填充信号过零时间的差值，并与参考信号整周期的填脉冲数相比较获得相位。此类方法应用最早，使用的硬件从早期的触发器、异或逻辑鉴相到目前的FPGA，高频脉冲的频率可高150MHz左右。通过算法的改进在抑制零点漂移、扩展测量范围、高效资源利用等方面都有了提升［10-11］。该方法的特点是硬件容易实现、精度高、实时性好，尤其是测量带宽大，可到理论极限值。但测量分辨率提高很大程度上依赖参考信号与高频脉冲的频率差值。由于目前FPGA器件的速度限制，此类方法的分辨率很难达到亚纳米级。

不少学者采用混频的方法，从频谱的角度，把叠加在fb上的多普勒频移Δf搬到新的低频信号上，并以该低频信号作为新的参考信号来提高测量分辨率［1，3，12-13］。其原理如图5所示。图中的参考信号即为转换后的低频信号。

图5 采用低频参考信号提高比相精度

由图5可知，非整周期的相位差为Δφ＝φ1－φ2。由（6）式可知：

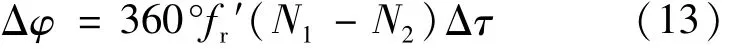
高频脉冲频率不变，N1，N2和Δτ保持不变，但参考信号采用频率更低的fr′，因此相位分辨率得以提高。参考文献［1］中通过混频把原747MHz的拍频信号降到0.1MHz，在保证±2.4m／s的测量速率下，测量精度可达0.15nm。

但采用这种方法，会引入前面提到的滤波器设计问题。可知混频的过程是频率变换的过程，会产生输入信号频率与本振信号的和频、差频信号。差频就是低频参考信号，而和频信号则需要通过带通滤波器滤除。而多普勒频移可正亦可负，和频信号与差频信号并没有明确的频率分割界限。因此，滤波器截止频率的设计决定了相位计的测量带宽。在最大测量带宽确定的情况下，此方法容易获得亚纳米级的测量精度。

其它常用的方式包括锁相环［9，12，14-16］和离散傅里叶运算［6，16］。前者常用于低频或超低频的外差干涉信号比相，如星间激光干涉测距和全球重力场反演。也可结合混频［12，15］、正交I／Q［9］技术等把高频测量信号变换为低频测量信号。在数字锁相中，通过预先存储拍频信号各相位对应的幅值来比相。比相精度依赖内存的容量，且容易受干涉信号幅值变化干扰。在相位取值40位时，比相计精度可达2″。后者利用傅里叶变换，实质是正交变换［17］，获取信号频谱分量的实部和虚部，通过反正切求得相位。该方法适用于静态周期信号测量，当测量信号频率动态变化时，即使采用加窗技术仍然无法避免非周期采样带来的误差。另外，为减小误差变换运算需要的采样点通常在十几个周期，实时性较差。因此离散傅里叶运算不适用干涉信号的动态比相。

3 结 论

综上所述，外差干涉仪的比相计需要对频率瞬时变化的测量信号与参考信号之间进行动态的相位测量。高性能的比相计在设计时需兼顾测量带宽（测量速率）及测量精度。本文中所述的几种方法在实际应用中经常混合使用以达到所需的测量指标。目前基于各类方法的比相计测量精度均能达到亚纳米级，但测量带宽则不够，无法满足高速测量状态下的应用。高速、高精度、实时动态测量是本领域发展的一个重要趋势。

［1］ KIM M S，KIM SW.Two-way frequency-conversion phase measurement for high-speed and high-resolution heterodyne interferometry［J］.Measurement Science and Technology，2004，15（6）：2341-2348.

［2］ AGILENT TECHNOLOGIES.Laser and optics user’s manual［DB／CD］.Clara，CA，USA：Agilent Technologies，2002：05517-90045.

［3］ YIM N B，EOM C I，KIM SW.Dual mode phase measurement for optical heterodyne interferometry［J］.Measurement Science and Technology，2000，11（3）：1131-1137.

［4］ DUANW W，YU L，LISJ.A king of improved CORDIC algorithm and its implementation in FPGA［J］.Microelectronics＆Computer，2012，29（2）：95-98（in Chinese）.

［5］ ZHANG JB，LIANG F，LIU N A.FPGA implement of amodified CORDIC algorithm［J］.Microelectronics＆Computer，2010，27（11）：181-184（in Chinese）.

［6］ ZHANG N.Soft ware method used in phase-measuring of space optical heterodyne system［D］.Wuhan：Huazhong University of Science and Technology，2010：12-16（in Chinese）.

［7］ WANG L，HOUW M.Single frequency laser interferometer based on Koester prism［J］.Measurement Technique，2006，11（1）：29-32（in Chinese）.

［8］ LIU X Q，LIU B，MA X P.High-precision intermediate-frequency digital phase detector based on FPGA［J］.Nuclear Techniques，2012，35（5）：380-385（in Chinese）.

［9］ WARE B，FOLKNERW M，SHADDOCK D，et al.Phase measurement system for inter-spacecraft lasermetrology［C］／／The Sixth Annual NASA Earth Science Technology Conference 2006.Maryland，MD，USA：NASA，2006：1-5.

［10］ QIU X Q，LE Y F，WANG J.Interpolation of heterodyne interferometric signals based on FPGA［J］.Laser Technology，2011，35（2）：199-201（in Chinese）.

［11］ SHIY，JU A S，LEY F.Heterodyne interference signal processing method based on FPGA［J］.Laser Technology，2012，36（2）：225-227（in Chinese）.

［12］ ZHANG G Z.Dual-differential phase discrimination phase measurement system based on PLL frequency-mixing［D］.Hangzhou：Zhejiang University of Science and Technology，2005：31-54（in Chinese）.

［13］ ZHAO SW，YAN L P，YANG T，etal.Signal processing method of the laser heterodyne interferometry based on DSP［J］.Journal of Zhejiang Science and Technology University，2011，28（2）：217-220（in Chinese）.

［14］ LIANG Y R，YE X J.High precision phase meter for inter-spacecraft laser metrology［C］／／China’s Space of Deep Space Exploration Technology Professional Committee of the Eighth Session of the Symposium.Shanghai：CDSET-CSA，2011：529-535（in Chinese）

［15］ MAGNUST LH，IAN CM L，DANIELA S，et al.Subpicometer length measurement using heterodyne laser inteferometry and alldigital rf phase meters［J］.Optics Letters，2010，35（24）：4202-4204.

［16］ JIANG Y Q，HE Y G.New algorithm for high-accuracy phase difference measurement based on windowed DFT［J］.Journal of Circuits and Systems，2005，10（2）：112-116（in Chinese）.

［17］ SONG Ch B，LI Zh G，ZHU X S.A method＆error analysis of phase difference measurement based on digital quadrature transformation［J］.Journal of Circuits and Systems，2006，11（1）：143-146（in Chinese）.

Design of phase comparator in a laser heterodyne interferometer

LE Yanfen，LI Xiaoxia，JU Aisong
（School of Optical-Electrical and Computer Engineering，University of Shanghai for Science and Technology，Shanghai 200093，China）

Phase comparison of the heterodyne signal determines the performance of the heterodyne interferometer to some extent，such as precision and resolution.To resolve the conflict between the resolution and the velocity，methods used presently to design the phase comparator were introduced and analyzed.Key design points to achieve high measureable velocity with fine resolution were discussed.Solutions to the problems were also proposed.The full period sampling method based on field-programmable gate array（FPGA）can improve the precision of autocorrelation and the zero-across detection with frequency mixing can improve the test speed.

measurement and metrology；heterodyne interferometry；phase comparator；phase measurement

TH744.3

A

10.7510／jgjs.issn.1001-3806.2014.01.026

1001-3806（2014）01-0119-05

国家自然科学基金资助项目（51075280）；上海市大学生创新创业训练计划资助项目（201210252025）

乐燕芬（1978-），女，博士研究生，讲师，现主要从事微纳米检测的研究。

E-mail：le_yf＠163.com

2013-03-25；

2013-05-17