基于分割缩放的欠采样相位图解包裹算法

徐天杰，钱晓凡，戴欣冉，李 斌

（昆明理工大学理学院激光研究所，昆明650500）

基于分割缩放的欠采样相位图解包裹算法

徐天杰，钱晓凡*，戴欣冉，李 斌

（昆明理工大学理学院激光研究所，昆明650500）

为了提取所需的相位信息，克服噪声、断点以及欠采样等不利因素的影响，针对采样问题出现的根本原因（采样频率过低、图像条纹密度过高），在处理欠采样问题时采用基于分割缩放原理的相位解包裹算法，对密度过高的干涉条纹通过插值放大后再进行解包裹运算。在理论分析的基础上给出了具体的相位解包裹算法，模拟计算和实验验证都表明了该算法的可行性。结果表明，该算法对有欠采样相位的解包裹能取得不错的效果。

全息；相位解包裹；分割缩放；欠采样

引 言

数字全息技术记录了可以反映物体表面2维形貌、形变、应力分布或温度场等信息的光场相位，所以，通过对数字再现象的相位进行提取与解包裹计算，就可实现包括2维形貌检测在内的各种测量，因而应用前景广阔［1］。在提取相位信息时由于通常要引入反正切函数，得到的相位称为包裹相位，即相位值介于（－π，π］之间，这就需要采用相位解包裹运算处理相位分布上的跳变点，将被截断（包裹）的相位连接起来，以得到真实的相位分布［2］。

实际问题中，由于噪声、断点，特别是欠采样等的影响，包裹相位中有大量不可靠数据点存在，使相位解包裹成了一个十分困难的问题［3］。目前相位解包裹最常用的算法是最小二乘法［4-6］，其中最小二乘法又分为无权最小二乘法［4，7］和加权最小二乘法［8-9］。针对欠采样造成的相位解包裹困难，作者在无权最小二乘解包裹算法的基础上，提出了基于分割缩放原理的相位解包裹算法，模拟计算和实验验证均表明，该算法对有欠采样相位的解包裹能取得不错的效果。

1 分割缩放原理

采样频率过低、图像条纹密度过高，是欠采样问题出现的根本原因，为此，如果对密度过高的干涉条纹通过插值放大后再进行相位解包裹处理，可以有效克服欠采样的发生。但在实际操作中，待解包裹图的分辨率一般都比较高，在进行插值放大后就会很容易出现超出计算机软硬件处理能力的情况。针对该问题，作者提出了基于分割缩放原理的相位解包裹算法：（1）将包裹相位图分割成若干个子单元；（2）对每个子单元进行插值放大处理；（3）对插值放大后的子单元块进行解包裹运算；（4）将解包裹后的子单元块缩小至原来的大小；（5）将缩小后的子单元块合并成为完整图像。

实际上，由于解包裹的过程是将断裂的条纹拼接起来的过程，在合并的过程中会带来条纹整体平移的问题，不调整相邻单元块之间相位值大小的直接合并操作，会使得各个小单元之间出现明显的断层，所以必须找到合理的合并方法。

2 一种扩散式的合并方法

前面已经说明，找到好的合并方法是本文中相位解包裹算法得以实现的关键，作者提出了下面的合并方法。

如图1所示，把待处理包裹相位图按顺序分割成数个子单元图，每个子单元大小均为（m+Δm）×（n+Δn）像素（处于最后一行和列的单元除外）。为避免简单合并所带来的错误，作者让相邻的两个子单元、最末端的子单元与余项单元之间存在Δm行和Δn列的重叠区域。完成对所有子单元的相位解包裹后，需要进行修正，修正过程要求对每个子单元加上一个增量δi，j，δi，j的值由相邻单元重叠区域的相位平均值决定。最后将校正过的解包裹单元合并起来，从而解决直接合并所带来的错误。

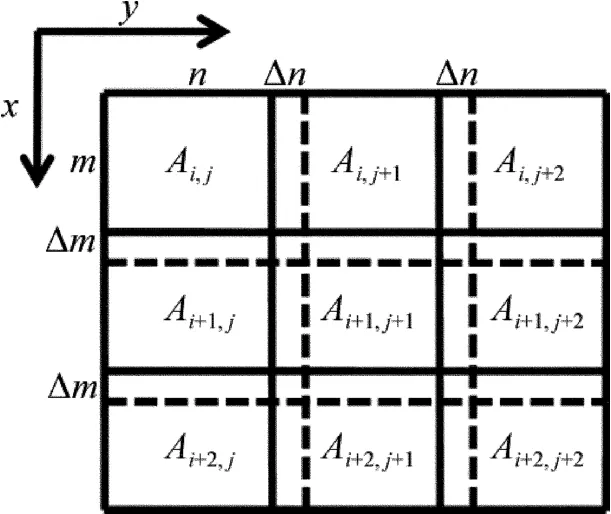
Fig.1 Schematic diagram of segmentation

当然，校正顺序不同，合并的方法也相应不同，选用的是一种扩散式的合并方法：该方法以左上角的子单元作为参考单元，然后沿x和y方向延展顺序校正其后的各个单元。

Ai，j（i＝0，1，…，L－1；j＝0，1，…，K－1）的大小为（m+Δm）×（n+Δn）像素；L是x方向上的子单元数，K是y方向上的子单元数，通常情况下，x和y方向的末端会出现与子单元大小不相同的余项单元。余项单元单独处理；子单元Ai+1，j和Ai，j有Δm行重叠区域，分块Ai，j+1和Ai，j有Δn列重叠区域。先确定第1个单元A0，0（i＝0，j＝0）为基准单元，然后分别计算其与右、下方向相邻单元A0，1和A1，0的增量δ0，1与δ1，0，再以A0，1和A1，0为基准依次计算下去。

子单元的处理方法如下：

（1）当i＝0，j＝0时，即确定初始的基准单元时，需要确定一个初始增量δ0，0，δ0，0的值通过对解包裹后的子单元进行再包裹，然后与原始包裹相位相减，再取差值的平均值得到。

（2）当i＝0且j＝1，…，K－1或i＝1，…，K－1且j＝0时，增量的取值分别为：

（3）当i＝L－1且j＝1，…，K－2或i＝1，…，K－2且j＝L－1时，增量的取值为：

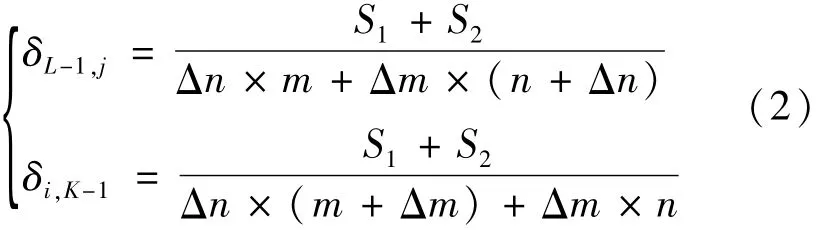
（4）当i＝L－1，j＝L－1时，增量的取值为：

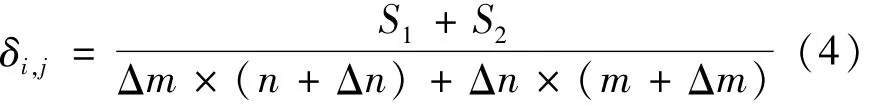
式中，

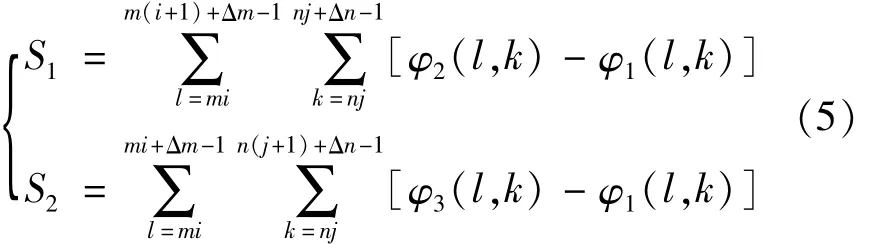
（5）其它情况下增量的取值为：

式中，φ1（l，k）是未经修正的子单元Ai，j的解包裹相位，φ2（l，k）和φ3（l，k）分别是子单元Ai－1，j和Ai，j－1经修正后的解包裹相位。

通过上述计算，可以对分割后的子单元块进行很好的合并处理。解决了图像合并这一关键问题后，使用本文中的方法解决欠采样图像相位解包裹的问题也就迎刃而解了。

3 基于分割缩放原理的欠采样相位图解包裹算法模拟计算

为了检验作者所提出的算法针对欠采样相位图解包裹是否能达到预期效果，现做以下模拟计算。

作者用MATLAB中的peaks函数再乘以20构建一个2维相位分布（512pixel×512pixel），如图2a所示，其包裹相位如图2b所示。使用传统的最小二乘法进行解包裹计算，结果如图2c所示，可以看出结果不是很理想，主要是由于peaks函数乘以20后其包裹相位变化太快，出现了欠采样。

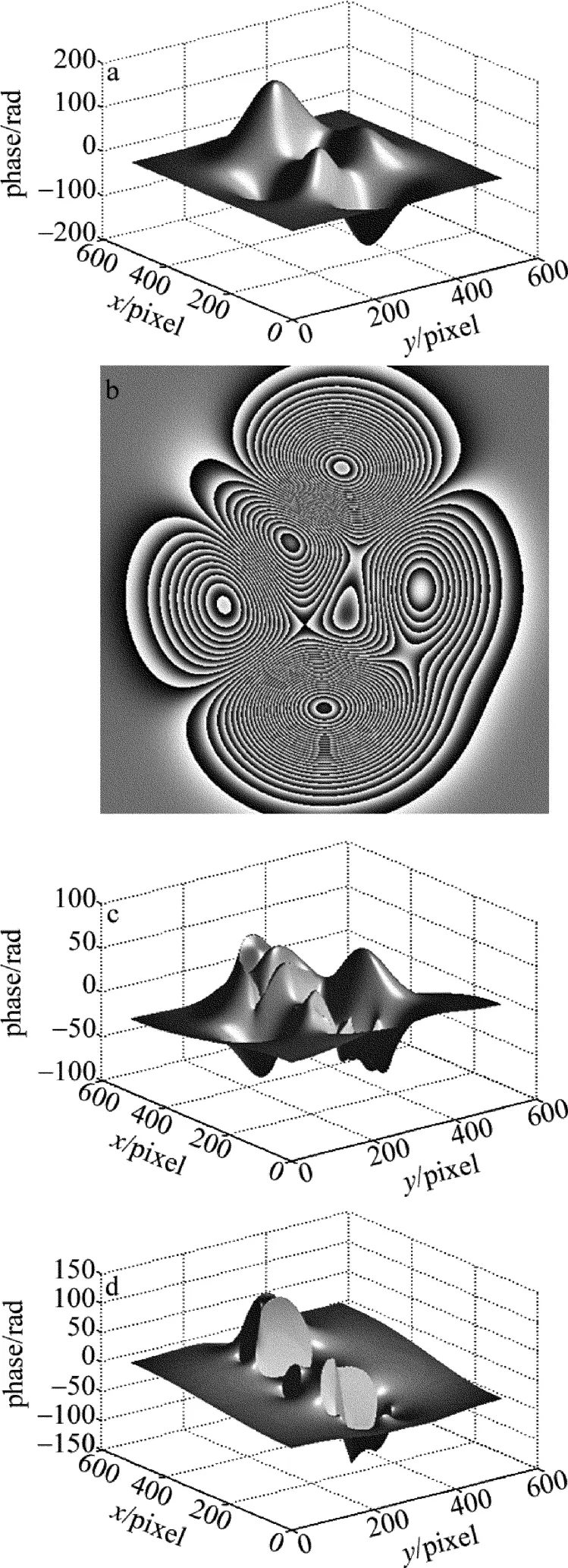
Fig.2 Simulated unwrapping results of wrapped phase with undersampling from least-square unwrapping operation

下面采用本文中的方法解包裹，为了观察解包裹的效果，作者给出了计算误差，即将解包裹得到的相位与原始相位相减，得到了几个典型的计算结果（X表示插值放大倍数）在图3中给出。结果显示，分割包裹相位图后进行适当缩放再完成解包裹计算，能很好地避免欠采样问题。

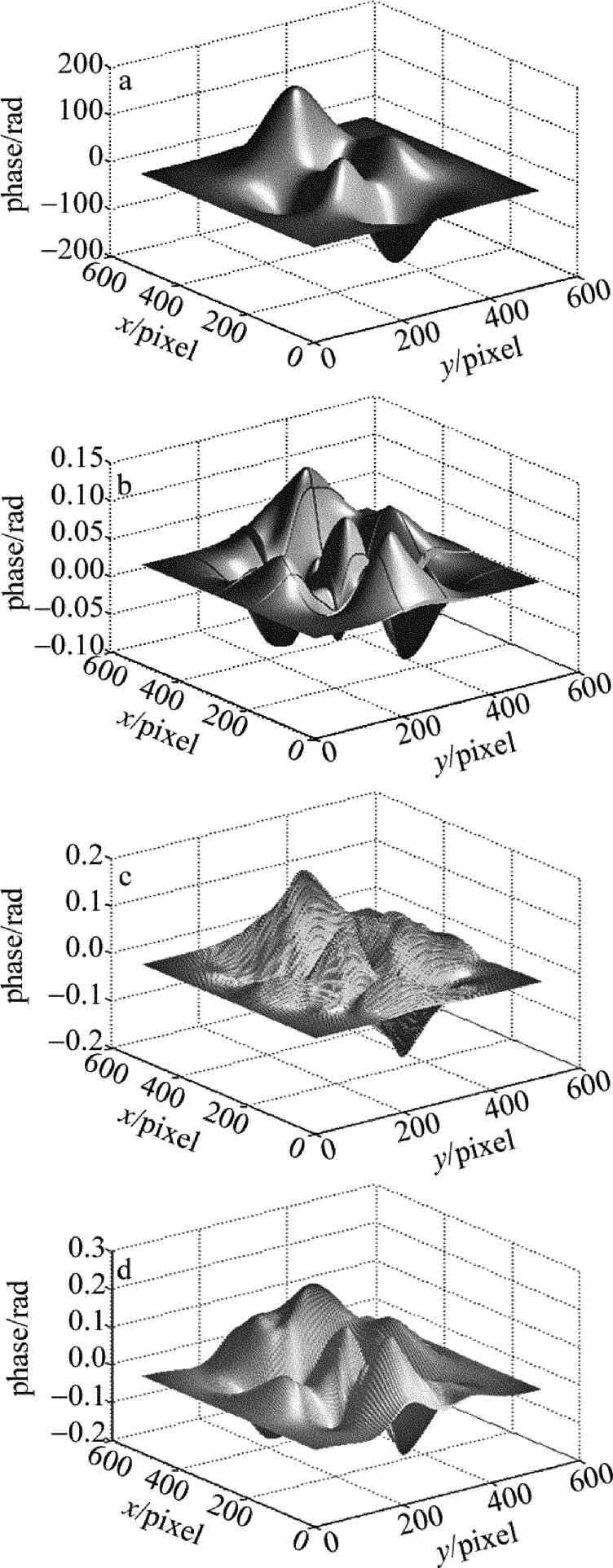
Fig.3 Simulated unwrapping results of wrapped phase with undersampling from segmentation and zooming unwrapping operation and the error

通过对比可以看到：使用最小二乘法对欠采样图像进行相位解包裹有很大的误差，而使用本文中的分割缩放解包裹算法解包裹，误差很小（最大相对误差不到0.5%）。放大倍数X越大，解包裹的效果越好。但是，放大倍数X越大，运算的速度越慢。

4 处理实验数据的验证结果

为了进一步检验所提出算法的效果，将其用于实验得到的有欠采样包裹相位图的解包裹，为此作者布置了如图4所示的实验光路［10］。激光束（波长为632.8nm）被分束镜（beam splitter，BS）BS1分为两束，其中一束经扩束系统（beam expanding system，BES）BES1和透镜L1变为平行光，再经反射镜M1和分束镜BS2反射后作为参考光到达CCD（2048pixel×1536pixel，像素大小为6.4μm）；另一束被反射镜M2反射，经扩束系统BES2和透镜L2变为平行光，再经透镜L3汇聚为球面波，最后通过分束镜BS2作为物光到达CCD。参考光、物光在CCD处干涉并记录下来得到数字全息图，送计算机处理。

Fig.4 Schematic experiment setup

图5 a是实际拍摄的一幅全息图，记录的是一个球面波的光场，通过减小球面半径，得到了包裹相位存在欠采样的数字全息图；图5b是对应的包裹相位图。

Fig.5 Digital hologram and wrapped phase

图6中给出了用不同算法对实验得到的有欠采样包裹相位图解包裹的结果。其中图6a中给出的是用传统的最小二乘法解包裹所得结果，与模拟计算一样，有欠采样发生时，用传统最小二乘法解包裹得到的相位有严重失真，误差很大；图6b中给出的是用常用的枝切法解包裹所得结果，由于有欠采样，大片区域无法顺利完成解包裹运算；图6c中是用作者提出的分割缩放方法解包裹结果，计算中取m＝n＝30，X＝10。可以看出，该方法解决欠采样问题的能力到达了预期的效果。

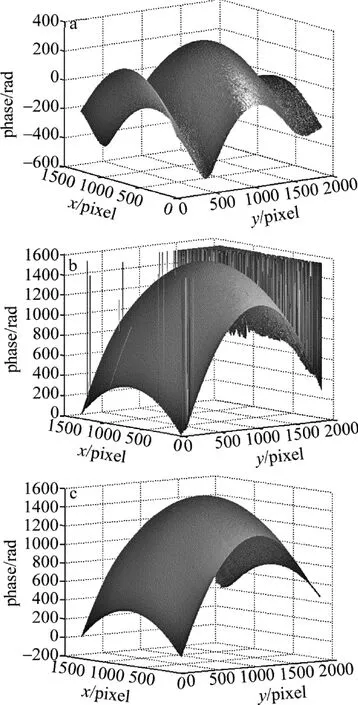
Fig.6 Experimental unwrapped phase by different unwrapping algorithm

5 结 论

由于噪声、阴影、条纹断裂及欠采样等因素的影响，包裹相位中有大量不可靠数据点存在，给最小二乘相位解包裹带来困难。本文中将分割缩放原理引入到数字全息再现光场的重构中，对密度过高的干涉条纹通过插值放大后再进行相位解包裹处理，提出了基于分割缩放原理的欠采样相位图解包裹算法，可以有效克服欠采样的发生。通过模拟计算得到了不错的效果，实验结果也验证了这种算法的可行性，该算法为有欠采样相位的解包裹提供了一种新的思路。

［1］ XU L，PENG X Y，ANAND A K，et al.Digital microholointerferometer development and validation［J］.Optical Engineering，2003，42（8）：2218-2224.

［2］ GE B Z，CUIP，LU Q N.Implement of phase unwrapping of digital holographic reconstruction image by discrete cosine transform least-square method［J］.Journal of China University of Petroleum（Natural Science Edition），2008，32（6）：1673-5005（in Chinese）.

［3］ ZHANG X，QIAN X F.An improvement on the least-squares phase unwrapping algorithm for undersampled interferogram［J］.Acta Photonica Sinica，2011，40（1）：121-125（in Chinese）.

［4］ PRITT M D，SHIPMAN JS.Least-squares two-dimensional phase unwrapping using FFT’s［J］.IEEE Transactions on Geoscience and Remote Sensing，1994，32（3）：706-708.

［5］ MENESESJ，GHARBIT，HUMBERT P.Phase-unwrapping algorithm for images with high noise content based on a local histogram［J］.Applied Optics，2005，44（7）：1207-1215.

［6］ HUIM，WANG D Sh，LIQ X，et al.Phase unwrapping method based on the solution of discrete poisson equation［J］.Acta Optica Sinica，2003，23（10）：1245-1249（in Chinese）.

［7］ GHIGLIA D C，REMORO L A.Robust two-dimensional weighted and unweighted phase unwrapping that uses fast transforms and iterative methods［J］.Journal of the Optical Society of America，1994，A11（1）：107-117.

［8］ QIAN K M，WU X P.Modulation analysis based on weighted least-squares approach for phase unwrapping［J］.Acta Photonica Sinica，2001，30（5）：585-588（in Chinese）.

［9］ QIAN X F.A new phase calculation method in 3-D optical phase measurement by combining PSP with IFTP［J］.Optoelectronics Letters，2010，6（2）：120-123.

［10］ LIB，QIAN X F，LIX H，et al.Phase-unwrapping algorithm based on radial shearing principle［J］.Laser Technology，2013，37（1）：44-47（in Chinese）.

Unwrapping algorithm based on segmentation and zooming for undersampled wrapped phase

XU Tianjie，QIAN Xiaofan，DAI Xinran，LI Bin
（Institute of Lasers，Faculty of Science，Kunming University of Science and Technology，Kunming 650500，China）

In order to obtain phase information，many unfavorable factors such as noise，breakpoint and under sampling must be overcome.Aimed at too low sampling frequency and high fringe density，the root cause of the undersampling problem，unwrapping algorithm based on segmentation and zooming principle was introduced.After enlarging interference fringe whose density is too high by interpolation method，the phase was unwrapped.The simulation and experimental results show the feasibility of the proposed algorithm.It turns out that it is an effective unwrapping algorithm for undersampled wrapped phase.

holography；phase unwrapping；segmentation and zooming；undersampling

O438.1

A

10.7510／jgjs.issn.1001-3806.2014.01.009

1001-3806（2014）01-0039-05

国家自然科学基金资助项目（61067004）

徐天杰（1986-），男，硕士研究生，现主要从事光信息处理方面的研究。

*通讯联系人。E-mail：qianxiaofan1＠sina.com

2013-04-16；

2013-05-16