基于优先度排序的3维数据缺失快速插补法

熊润华，张启灿

基于优先度排序的3维数据缺失快速插补法

熊润华，张启灿*

（四川大学光电科学技术系，成都610064）

为了快速准确地对3维光学测量的缺失数据进行插值，以利于后期对比研究，提出了基于优先度排序的3维数据缺失快速插补估算方法，并把该算法用于插补模拟实验数据以及20帧振动扬声器测试数据的验证。结果表明，与其它常用缺失数据插补方法相比，该方法运算速度快、插补效果好，有利于处理3维测量结果的多帧和大量的数据。

信息光学；3维面形测量；优先度；数据插补

引 言

在现代测量方法中，3维面形光学测量方法以其特有的众多优良特性，被广泛地应用于众多行业中。现有的方法包含莫尔条纹法（Moiré technique，MT）［1］、傅里叶变换轮廓术（Fourier transformation profilometry，FTP）［2-3］、相位测量轮廓术（phasemeasuring profilometry，PMP）［4-5］、调制度测量轮廓术（modulation measurement profilometry，MMP）［6］、空间相位检测（spatial phase detection，SPD）［7］和光学三角测量法［8-9］等。就其本质而言，都是通过分析受物体表面面形调制的光场，解调出物体的高度信息。用基于条纹投影的3维面形光学测量方法对静态物体进行3维测量时，如果待测量物体面形比较复杂，则会出现采样不足或阴影现象，导致相位信息中出现极点［10］，进而使得局部数据缺失。在采用多角度测量方式重建物体3维面形时，通常需在物体表面附加标记点处通过辅助匹配来完成拼接［11］。由于附加了标记点，无法同时得到标记点覆盖处的物体相位信息，因此也会导致标记点覆盖区域数据的缺失。动态过程3维面形重建方法以FTP为基础，通过结构光照明和高帧频的CCD摄像机快速获取［12］动态过程中的一系列变形条纹图，再经过傅里叶变换、频谱滤波、逆傅里叶变换、3维相位展开等处理［13］后得到一系列重建的3维面形。一般情况下，需用高帧频成像设备沿时间轴采样量化，用重建的多帧3维数据结果表征不同瞬间的3维面形，为了将此动态过程集中对比分析，就需要将多帧3维数据统一映射到同一坐标系内。在映射的过程中，由于物体的运动变化会导致不同坐标系向最终坐标系统一映射时，一些点上没有数据值。如何快速和准确地插补，还原出这些缺失值点的3维坐标信息是本文中研究的主要问题。国内外在图像处理方面常用的插补方法有：邻域均值法、邻域加权平均法［14］、傅里叶变换迭代法［15］、八方向梯度估算法［16］。权重算法根据有效点与待插补点的距离远近设置不同的权重，考虑到了距离对待插补点值的影响，在处理较大邻域变化的数据时邻域加权平均要优于邻域均值法［16］。由于邻域加权平均法是依靠大量有效值点的加权平均值得到数据，在处理有少量尖刺数据时有一定的抗干扰能力。但是没有充分考虑物体的局部变化趋势，当待插补区域位于倾斜面上且具有一定面积时（如标记点处），会引起较大的误差。八方向梯度估算的梯度算法是一种基于对数据变化趋势进行分析得到的缺失点数据的方法。但确定梯度时在同一条梯度方向上至少要有两个有效值，如果其中一个为尖刺干扰数据时，这种对趋势的估算容易将干扰扩大。因此，作者的研究工作拟将二者结合起来，充分利用它们各自的优点，对应处理不同情况下的数据缺失插补问题；同时，原有算法都是对插补数据区域采用“数据挤压缝合”，每次插补边沿点都需要做一次全局扫描，这样将耗费大量的时间，而降低插补的速度。作者提出将梯度权重相结合的估算方法，并按优先度大小排序先后对缺失数据进行插补，该算法能够通过一次扫描就得到所有待插补点的插补顺序，从而克服了现有方法的反复搜寻耗时，而且保持较快运算速度的同时，插补的数据更接近物体的实际形状，能比较快捷地获得理想的插补效果。

1 本文中的算法原理

1.1梯度和权重相结合的估算方法

结合八方向梯度估算法和加权平均算法的优点，在插补数据的时候既可以处理斜面大面积数据缺失值点的问题，又可以在一定程度上减弱由于各种干扰对待插补值的影响，在插补数据的准确性上相比单一算法有了较大的提高。本文中的算法通过对有效值点位置分布不同采用不同的方法取估算值。两种算法的结合使用情况，以待插补点为对称中心，若有效值点是对称的，则进行权重相加运算，用有效值点的加权数据之和除以权重系数之和得到加权平均值w（x，y）。若有效值点不对称则进行梯度运算，即用有效梯度值的和除以有效梯度个数得到梯度算法平均值g（x，y），再将两个值相加求均值得到待插补数据的最终结果。具体计算过程如图1所示，以待插补点（x，y）为对称中心取一子窗口（5×5窗口），图中浅灰色点和黑色点为有效数据点，白色点为没有数据值的点，中间深灰色点（x，y）为待插补点。黑色点关于（x，y）点对称，进行权重运算得到w（x，y），其中A（x，y）为点（x，y）的有效数据点。

Fig.1 Combination algorithm

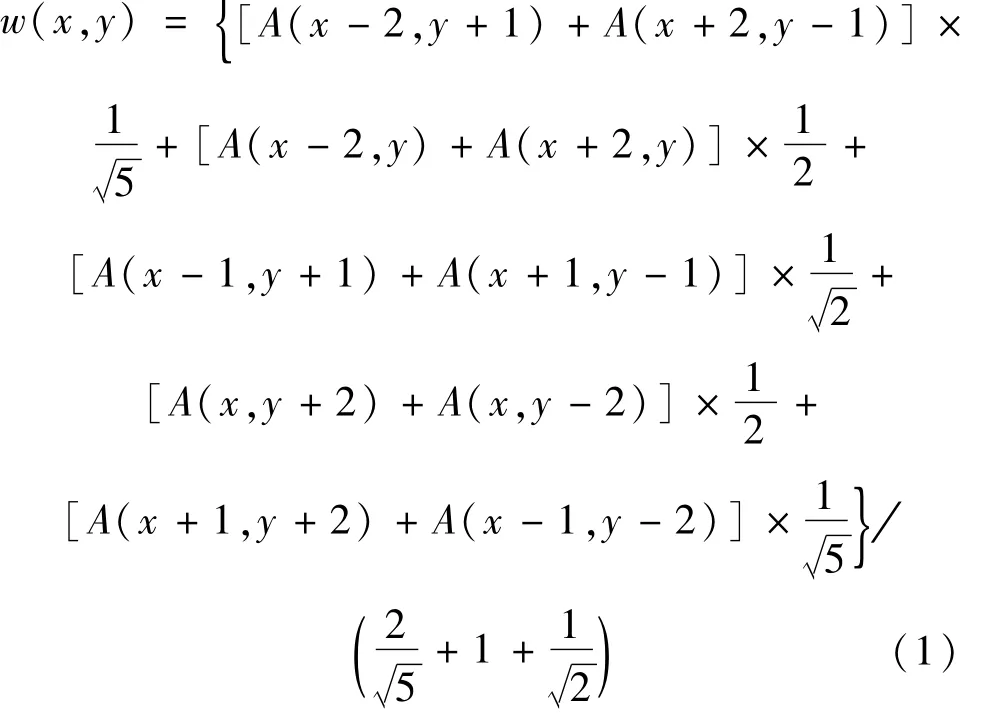
浅灰色点关于（x，y）不对称，对其进行梯度运算得到g（x，y），其中，

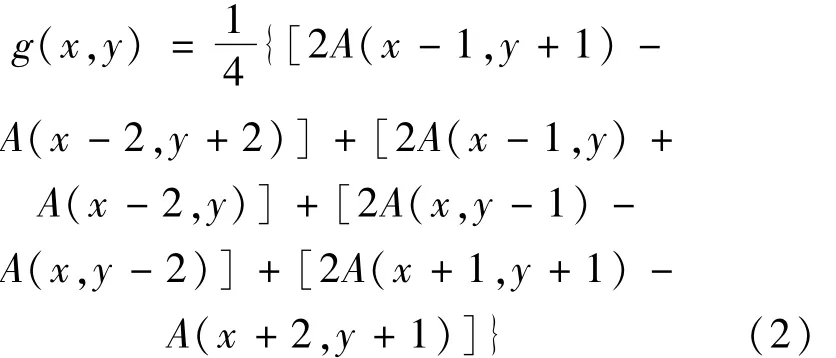
设（x，y）点缺失的数据估算值为V（x，y），则该条件下待插补点的数据估算值：

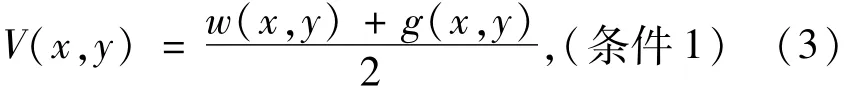
另外，当数据中只存在权重均值运算（或者既无对称有效数据值点也无有效梯度值点），则用权重均值来获得待插补点的数据估算值，即：

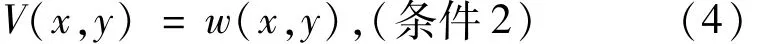
当数据中只存在梯度运算时，则用梯度运算值表示待插补点的数据估算值，即：

1.2缺失数据优先度排序

如果多点插补缺失数据在空间坐标上相邻成片，在这种情况下，为了尽量减小误差常常采取“数据挤压缝合”，从缺失数据区域的边沿开始向中间逐次进行插补，这样插补出来的结果的总体误差最小，使误差向中心堆积，能保证边沿缺失点具有较高精度［12］。插补效果拥有渐变性，而且最大限度地使用了有效值点。在现有算法中，使用“数据挤压缝合”方法在计算机上插补数据，每次选择确定待插补边沿点时，都需要对全局进行扫描，这样的操作将耗费大量的时间，甚至超过了插补过程中本身计算耗费的时间。为了能够通过一次扫描就得到所有待插补点的插补顺序，提出了优先度排序的算法，仅对全局数据进行一次扫描，确定它属于第几级边沿点，并依次对不同缺失数据点赋予不同的优先度，反映它们随后被插值处理的先后顺序，从而节省了今后再次扫描所要耗费的时间，加快了整个插值算法速度。具体判定令待插补点（x，y）优先度的初始值为a＝1，判断点（x，y）上下左右a（其中a＝1，2，3）点内是否有有效数据点，如有则得到其优先度是a。本文中采用的最大优先度为3。取一子窗口（9×9窗口），采用该种判定方法其优先度示意图如图2所示（黑色点为有效数据的点，非黑色部分为待插补点，数字表示此点的优先度），这样所有待插补点的优先度可以确定下来。

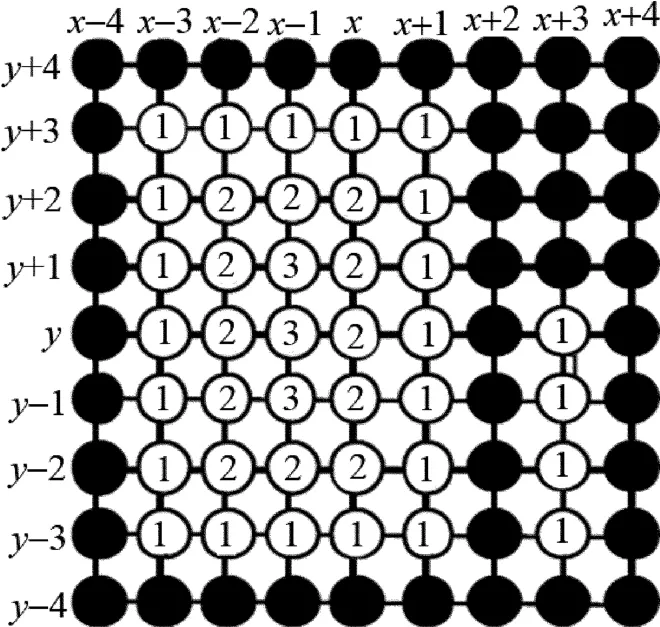
Fig.2 Priority schematic diagram

1.3算法的整体流程

本文中算法的整体流程可分为前期数据处理部分和后期数据插补过程。算法过程描述如下。

（1）前期数据处理部分，通过一次扫描加多次判断得到所有待插补点的插补顺序即优先度，确定它属于第几级边沿点并记录下处理的先后顺序。图3为前期处理部分程序流程图的主要部分，在此部分首先生成一个mask函数用来标记哪些位置的点是待插补点，令有效值点在mask中赋1，待插补点赋0。再将这些位置信息赋予（x（i），y（i））（其中i表示第i个待插补点）。取一个变量a＝1，再取一个待插补点，查看它上下左右4个方向有无有效值点，如果没有则表示第1次插补时它不在边沿点上，令a＝a+1，重复上述比较，直到有有效值点时为止，然后将现在的a值赋予优先度记录矩阵，得到此点的优先度系数。在实际编程中，为了提高速度将最大优先度值a设为一个合理的数，采用待处理数据中最大连续缺失值点数除以2然后向下取整，本文中使用的最大优先度值是3。

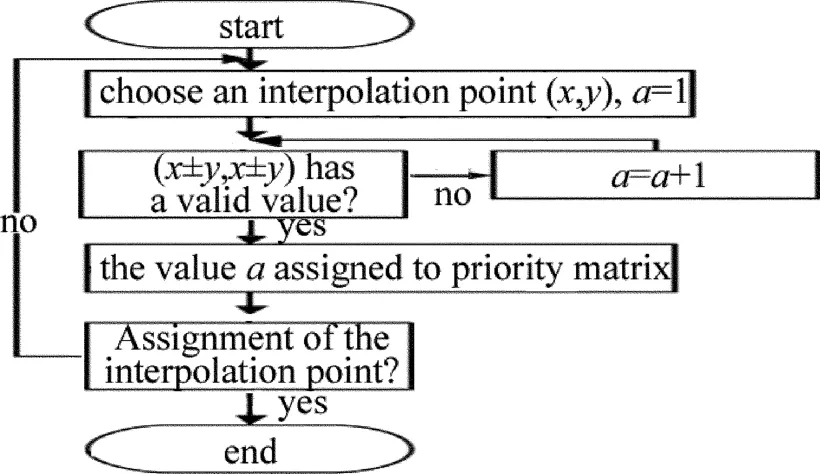
Fig.3 Early part of the program

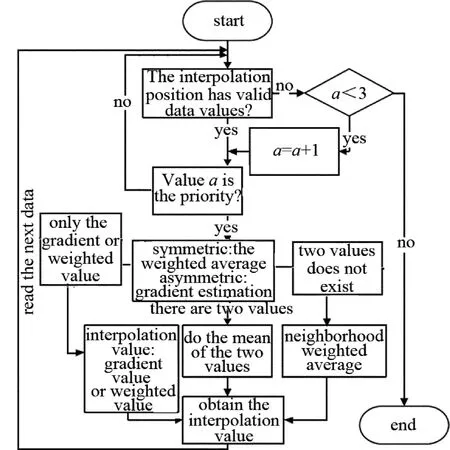
Fig.4 Late processing part of the program

（2）在后期插补的过程中，按照优先度1～3的顺序进行插补计算。图4为后期处理部分主要程序流程图。首先判断是否存在待插补点，若存在则取一待插补点，查询其优先度值，为当前处理优先度值则开始处理，否则查看下一待插补点；插补时取5×5邻域，采用前文提到的梯度和权重相结合的估算方法进行计算，计算结束后将这个位置的mask值赋1，表示此位置已经插补完成，然后再处理下一个待插补点。当优先度为1的数据都计算结束后，开始计算优先度为2的数据，直到计算全部完成，本文中只需将优先度不大于3的数据全部计算完毕。

2 新算法的模拟实验分析

实验数据为生成的peaks函数，人为对其随机删除一些有效值点，形成一个带有缺失值点的3维面形分布，如图5a所示；数据缺失区域见图5b；对此图像前期进行优先度判断，后期梯度权重相结合估算法进行插补运算，如图5c所示；用八方向梯度估算和加权平均算法处理图5a，分别得到插补效果图如图5d和图5e所示；3种估算算法的2维误差图分别见图5f、图5g和图5h。几种估算算法的插补标准差和运算时间如表1所示。由图5和表1可知，无论是插补结果的标准差，还是运行时间上，基于优先度排序的梯度权重相结合估算法都要优于单独的加权平均法和八方向梯度估算法。图中，H表示高度。

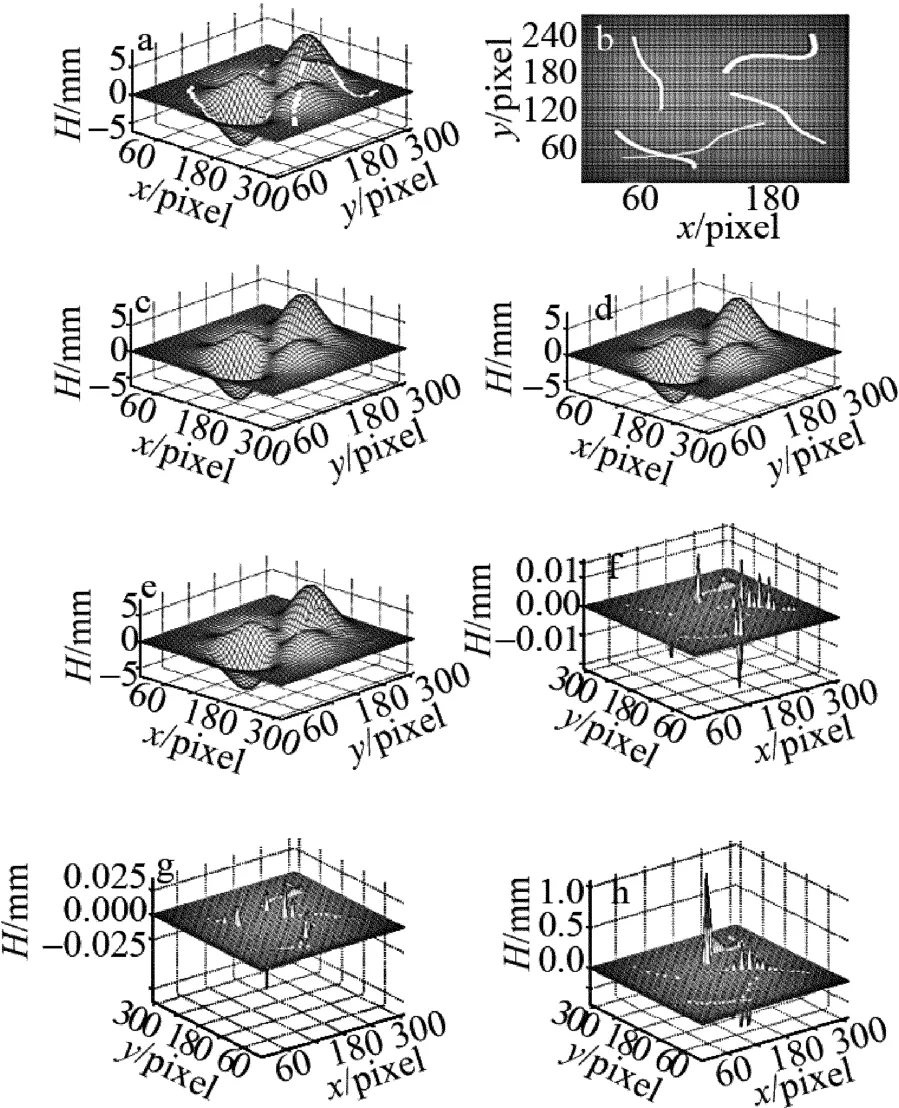
Fig.5 Interpolation of simulation experiment data

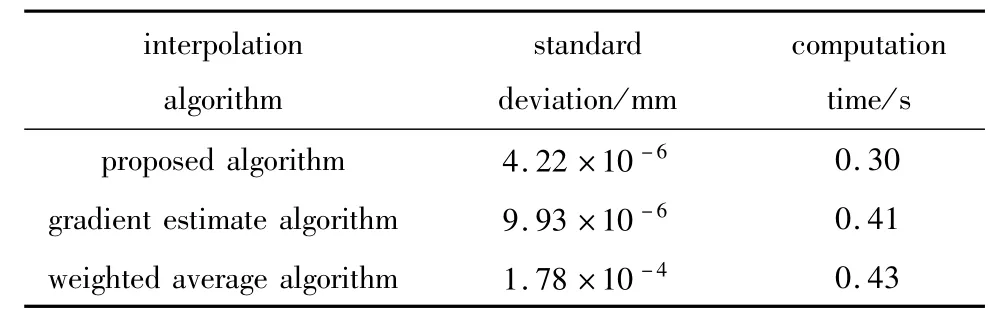
Table1 The standard deviation and the computation time

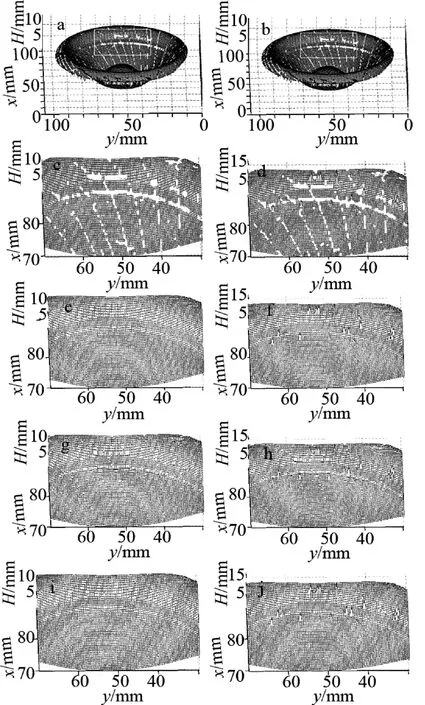
Fig.6 Interpolation results

3 对动态3维测量多帧数据的插补分析

使用液晶显示数字投影仪，投影正弦光栅周期为2.4mm，高速CMOS相机（Photonfocus MV2-D12 80-640-CL镜头焦距为50mm，系统测量精度为20μm），图像采集卡采集图像的速度为200frame／s，被捕获的图像的分辨率为1280像素×1024像素。对重建的振动扬声器20帧3维面形数据进行插补，矩阵大小为531×521点阵（每点阵对应统一坐标的x-y面内间隔为0.2mm），几种算法在插补每一个点时所考虑的邻域范围同为5×5点阵。分别用本文中基于优先度排序的权重梯度估算法、加权平均法和八方向梯度估算法进行插补，分析比较插补效果以及插补时间。图6a和图6b分别为第1帧、第14帧的原始数据，线框部分缺失数据比较多，容易出现插补误差，可以用于分析比较几种算法在误差比较大时的插补效果；图6c和图6d为放大的线框区域；图6e和图6f为本文中算法插补后效果；图6g和图6h为邻域加权平均算法插补后效果；图6i和图6j为八方向梯度算法插补后的效果。从图6可以看出，即使是在插补误差比较大的情况下本文中基于优先度排序，并且权重梯度相结合的估算新算法插补出的数据更为连续光滑。表2为3种算法对20帧扬声器数据处理的插补时间，从表2中可以看出，邻域加权平均算法和八方向梯度估算法的插补时间是新算法插补时间的2倍。对以上各帧的插补可以看出，新算法能对扬声器进行很好的插补，而且插补速度明显优于其它算法。

Table 2 The computation time

4 结 论

在3维面形测量中，针对缺失数据的处理，提出了前期优先度排序，后期权重和梯度相结合估算的新算法。用模拟实验数据和20帧扬声器振动数据验证了该方法可以快速、准确地插补出这些缺失数据。新算法在保证数据质量的前提下提高了处理速度，不仅便于静态3维面形缺失数据的插补，而且利于动态测量中的多帧、大量数据的插补处理。

［1］ TAKASAKIH.Generation of surface contours by Moire pattern［J］.Applied Optics，1970，9（4）：942-947.

［2］ SU X Y，LIJ，GUO L R.An improved Fourier transform profilometry［J］.Proceedings of SPIE，1988，0954：32-35.

［3］ TAKEDA M，MUTOH K.Fourier transoform profilometry for the auto measurement of 3-D object shapes［J］.Applied Optics，1983，22（24）：3977-3982.

［4］ SRINIVASAN V，LIU H C，HALIOUA M.Automated phase measuring profilometry of 3-D diffuse object［J］.Applied Optics，1984，23（18）：3l05-3108.

［5］ SU X Y，ZHOU W S，Von BALLY C，et al.Automated phasemeasuring profilometry using defocused projection of a Ronchigrating［J］.Optics Communications，1992，94（6）：561-573.

［6］ SU L K，SU X Y，LIW S.Application ofmodulation measurement profilometry to objects with surface holes［J］.Applied Optics，1999，38（7）：1153-1158.

［7］ TOYOOKA S，IWASA Y.Automatic profilometry of 3-D diffuse objects by spatial hhase detection［J］.Applied Optics，1986，25（10）：3012-3018.

［8］ CHENG X X，SU X Y，GOU L R.Automaticmeasurementmethod for 360°profilometry of 3-D diffuse objects［J］.Applied Optics，1991，30（10）：1274-1278.

［9］ LUO X H，JU Y，WANG X，et al.3-D foot profile measurement through light section method［J］.Laser Technology，2001，25（4）：308-311（in Chinese）.

［10］ GOLDSTEIN R M，ZEBKER H A，WERNER C L.Satellite radar interferometry：two dimensional phase unwrapping［J］.Radio Science，1988，23（4）：713-720.

［11］ MA Y B，ZHONG Y X，DAIX L.A method for 3-D scanning and reconstruction based on coded points［J］.Optical Technique，2006，32（6）：865-868（in Chinese）.

［12］ XIAO Y S，SU X Y，ZHANGQ C，etal.3-D surface shape restoration for the breaking surface of dynamic process［J］.Laser Technology，2006，30（3）：258-261（in Chinese）.

［13］ WU Ch C，SU X Y.Dynamic 3-D shape detected［J］.Journal of Optoelectronics＆Laser，1996，7（5）：273-278（in Chinese）.

［14］ RAFAEL CG，RICHARD EW.Digital image processing［M］.2nd ed.Beijing：Publishing House of Electronics Industry，2003：91-95（in Chinese）.

［15］ QIAN K.A simple phase unwrapping approach based on filtering by windowed Fourier transform：the phase near edges［J］.Optics＆Laser Technology，2007，39（7）：1364-1369.

［16］ HOU Zh L，ZHANGQ C，SU X Y.A novel missing phase interpolation algorithm for the branch cut and the marked point［J］.Optical Technique，2009，34（7）：502-505（in Chinese）.

Estimation method of fast interpolation of 3-D data based on priority

XIONG Runhua，ZHANG Qican
（Department of Opto-electronics，Sichuan University，Chengdu 610064，China）

In order to interpolate these missing data of 3-D measurement quickly and accurately and achieve further comparison study，the estimation method of fast interpolation of 3-D data based on priority was proposed.This algorithm was used to interpolate both the data of simulation experiment and twenty frames vibrating speaker.Compared with other common interpolation algorithm，this new algorithm is time-saving and its result is much better.It can be used to handle large amounts of data of 3-D shape measurement.

information optics；3-D measurement；priority；interpolation data

0438

A

10.7510／jgjs.issn.1001-3806.2014.01.007

1001-3806（2014）01-0030-05

教育部新世纪优秀人才支持计划资助项目（NCET-11-0357）

熊润华（1987-），女，硕士研究生，现主要研究光信息处理及3维传感技术。

*通讯联系人。E-mail：zqc＠scu.edu.cn

2013-04-01；

2013-05-10