材料色散对光子晶体全反射隧穿光场分布的影响

刘启能，刘 沁

（1.重庆工商大学计算机科学与信息工程学院，重庆400067；2.重庆工商大学设计艺术学院，重庆400067）

材料色散对光子晶体全反射隧穿光场分布的影响

刘启能1，刘 沁2

（1.重庆工商大学计算机科学与信息工程学院，重庆400067；2.重庆工商大学设计艺术学院，重庆400067）

为了研究材料色散对光子晶体全反射隧穿光场分布的影响，利用特征矩阵，推导出1维光子晶体中的光场分布公式。又利用光场分布公式和材料色散公式，研究了材料色散对1维掺杂光子晶体全反射隧穿光场分布的影响。结果表明，材料色散对1维光子晶体全反射隧穿的光场分布会产生明显的影响，材料色散会使全反射隧穿光场的峰值发生明显变化，并会使光场分布的周期性发生明显改变。此研究结果加深了对1维光子晶体全反射隧穿现象的认识。

光电子学；光子晶体；色散；全反射隧穿；光场

引 言

所谓光子晶体就是其折射率在空间成周期性排列的人造功能性材料。自从1987年光子晶体的概念被提出后，由于光在光子晶体传播时受到周期性结构的作用会在光子晶体内部产生光的带隙机构［1-6］，利用光子晶体的带隙可以十分方便地控制光波的传播。因此，对光子晶体的研究成为光学前沿领域内一个活跃的课题［7-13］。

作者利用光在介质中的色散关系研究了介质色散对1维光子晶体全反射隧穿效应的影响［14］，发现介质材料的色散会对1维光子晶体中全反射隧穿导带产生明显的影响，全反射隧穿导带的频率中心都随色散强度的增加而降低，频率宽度都随色散强度的增加而增大。最近作者又对1维掺杂光子晶体中偏振光缺陷模的光场分布开展了研究［15］，得出了1维掺杂光子晶体中偏振光缺陷模的光场分布特征。那么材料的色散是否会对1维光子晶体全反射隧穿效应的光场分布产生影响呢？这是一个值得研究的新问题。下面将建立材料的色散关系，并推导TE波在1维光子晶体中光场的分布公式，然后利用材料的色散关系研究色散对1维光子晶体全反射隧穿效应光场分布的影响。

1 理论模型

1.1 材料的色散

用洛伦兹振子模型来模拟色散材料的介电常数［14］有：

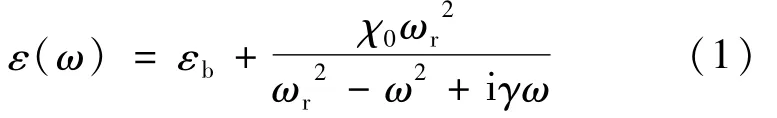
式中，εb，ω，ωr，γ和χ0分别为背景材料的介电常数、入射光的圆频率、材料的谐振圆频率、衰减系数和色散强度。改变εb，ωr，γ和χ0等参量，将改变介质材料的色散特性。由（1）式可知，材料的介电常数为复数，其折射率也为复数，称为材料的复折射率。复折射率的实部描述材料对光的折射性质，复折射率的虚部描述材料对光的吸收性质，下面仅研究复折射率实部的色散特性。

由（2）式可看出，在影响折射率色散特性的诸多因素中色散强度χ0是最重要的因素，χ0＝0表示材料无色散；χ0≠0表示材料有色散。

1.2 光场分布公式

设TE波在1维光子晶体中的传播，如图1所示。TE波在入射空间电矢量为E0、磁矢量的切向分量为H0∥，TE波通过1维光子晶体中任意一层Δzm后的电矢量为E、磁矢量的切向分量为H∥。根据特征矩阵的关系有：

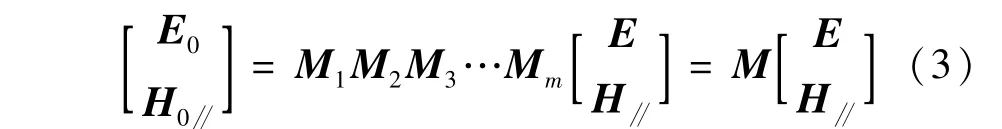
式中，Mi为TE波通过第i层介质中的特征矩阵，M为TE波通过前m层介质中的特征矩阵。由（3）式得：

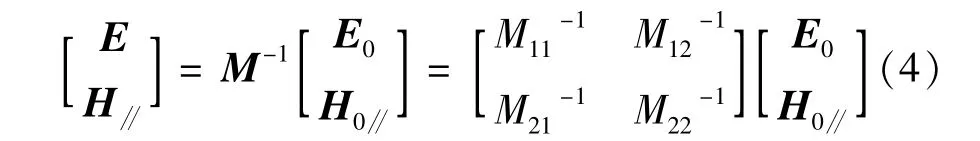
式中，M11－1，M12－1，M21－1和M22－1为矩阵元，展开（4）式有：

由图1可知：

Fig.1 Light intensity of TE wave in 1-D photonic crystal

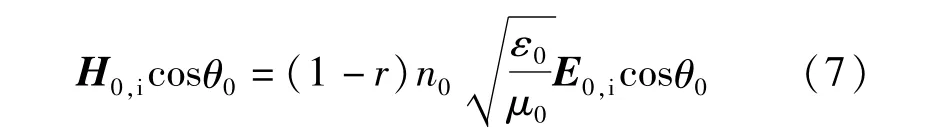
（6）式和（7）式中的r是该1维光子晶体对TE波的反射系数。

将（6）式和（7）式代入（5）式得：

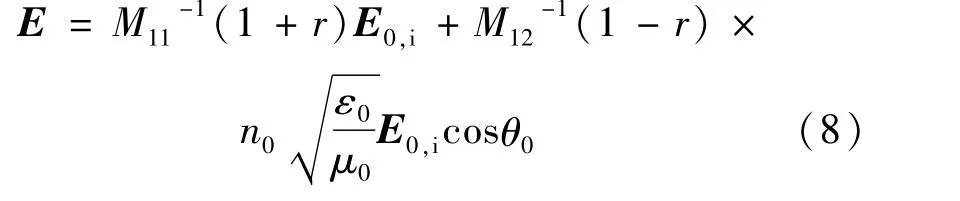
由（8）式得出TE波在1维光子晶体中任意一层Δzm后光场的分布公式：

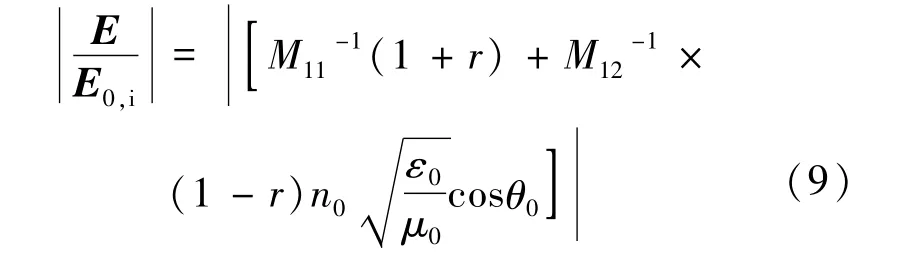
利用（9）式可以研究TE波在1维掺杂光子晶体中光场的分布规律。

2 色散对全反射隧穿光场的影响

设1维光子晶体的结构为（AB）N＋0.5，为了研究方便，选介质A为色散材料，其复折射率实部n1满足（2）式，取εb＝1.9，ωr＝8×1014Hz，γ＝4×1014Hz，考虑色散时取χ0＝0.4，不考虑色散时取χ0＝0，厚度为d2。介质B为非色散材料硫化锌（其折射率为n2＝2.38、厚度为d2）。两种介质周期性地交替构成。设入射空间和出射空间的介质也为硫化锌，即n2＝n0。因n0＞n1，所以当光大于全反射角入射该光子晶体时会产生全反射现象，在不考虑介质A的色散时，其全反射角为θm＝arcsin（n1／n0）＝0.62rad。取N＝5，n1d1＝n2d2＝λ0／4，λ0＝60nm，对应波长λ0的圆频率ω0＝2πc／λ0，c为真空中光速。

在不考虑介质A的色散时（χ0＝0），利用特征矩阵法计算当入射光的圆频率ω＝1.5ω0的TE波入射该1维光子晶体时，其透射率随入射角的响应曲线，如图2所示。由图2可以看出：当TE波大于全反射角入射时，在入射角θ0＝0.86rad～0.95rad范围内出现了多个明显的透射峰，即出现了全反射隧穿现象。大于全反射角的其它角度的透射率为0。

固定θ0＝0.91rad，利用特征矩阵法计算出介质A无色散（χ0＝0）和介质A有色散（χ0＝0.4）两情况下透射率随频率的曲线响应曲线，如图3所示。在图3中实线表示无色散（χ0＝0）的情况，虚线表示杂质有色散（χ0＝0.4）的情况。由图3可以看出：材料的色散对1维光子晶体的全反射隧穿峰的影响十分明显，色散会使全反射隧穿的5个峰向高频方向移动，色散会使相邻隧穿峰的频率间距减小，色散会使隧穿峰的频率宽度减小。

Fig.2 Response curves of transmissivity versus incident angle

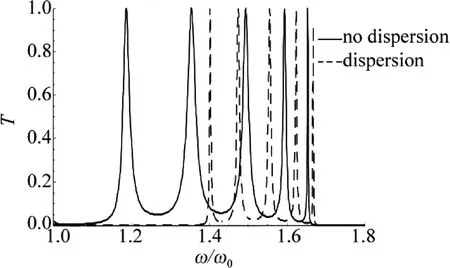
Fig.3 Response curves of transmissivity versus frequency

下面进一步研究材料的色散对1维光子晶体全反射隧穿效应光场分布的影响。由图3可以看出，圆频率ω＝1.49ω0处是材料无色散时中间全反射隧穿峰（第3个）的位置，圆频率ω＝1.56ω0处是材料有色散时中间全反射隧穿峰（第3个）的位置，下面研究这两个频率位置1维光子晶体中光场的分布。

2.1 ω＝1.49ω0时的光场分布

固定θ0＝0.91rad，ω＝1.49ω0，利用（9）式计算出TE波在无色散（χ0＝0）和有色散（χ0＝0.4）的情况下光场随透射深度的响应曲线，如图4所示。在图4中实线表示无色散（χ0＝0）的情况，虚线表示有色散（χ0＝0.4）的情况。透射深度D以一个周期的光程厚度为单位，整个1维光子晶体的透射深度范围为0.0～5.5，而5.5～7.0为透射空间。

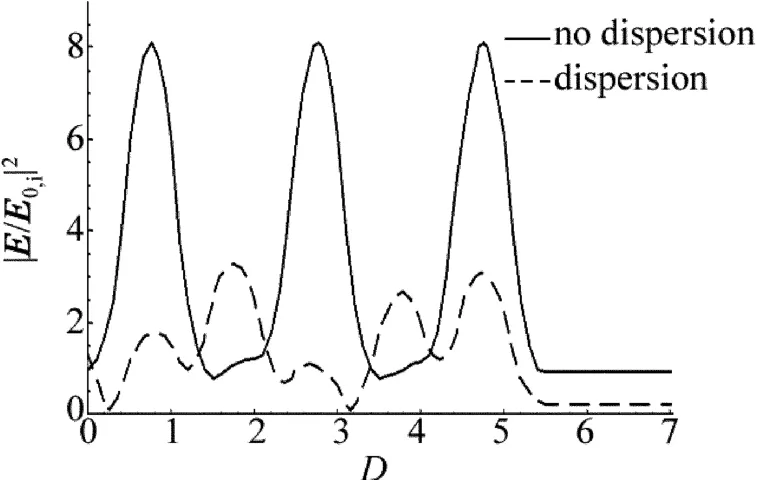
Fig.4 Response curves of light field versus depth of transmission（ω＝1.49ω0）

（1）无色散时光场的分布特征。无色散时光在光子晶体内部的场分布（实线）周期性地出现了3个分布峰，3个分布峰分别出现在透射深度D为0.8，2.8和4.8处，其光场的峰值达到8。这表明在1维光子晶体全反射隧穿峰值处，光子晶体内部光场的分布具有周期性，并且光场的分布很强。透射空间光场保持0.96不变。

（2）有色散时光场的分布特征。考虑材料有色散时，ω＝1.49ω0处的透射率T仅为0.2，不是全反射隧穿峰值的位置。其光在光子晶体内部的场分布（虚线）没有明显的规律，不具有周期性。光场最大位置出现在透射深度D＝1.7处，其光场为3.2。光子晶体内光场的分布较弱。透射空间光场保持0.2不变。

2.2 ω＝1.56ω0时的光场分布

固定θ0＝0.91rad，ω＝1.56ω0，利用（9）式计算出TE波在无色散（χ0＝0）和有色散（χ0＝0.4）的情况下光场随透射深度的响应曲线，如图5所示。在图5中实线表示无色散（χ0＝0）的情况，虚线表示有色散（χ0＝0.4）的情况。

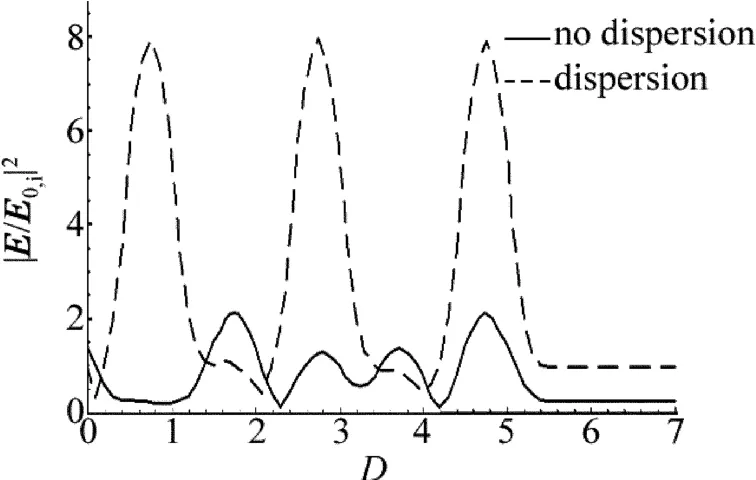
Fig.5 Response curves of light field versus depth of transmission（ω＝1.56ω0）

（1）无色散时光场的分布特征。无色散时，ω＝1.56ω0处的透射率T仅为0.18，不是全反射隧穿峰值的位置。其光在光子晶体内部的场分布（实线）没有明显的规律，不具有周期性。光场最大位置出现在透射深度D＝1.7处，其光场为2.2，光子晶体内光场的分布较弱。透射空间光场保持0.18不变。

（2）有色散时光场的分布特征。考虑材料有色散时，ω＝1.56ω0处的透射率T为0.97，是全反射隧穿峰值的位置。光子晶体内部的场分布（虚线）周期性地出现了3个分布峰，3个分布峰分别出现在透射深度D为0.8，2.8和4.8处，其光场的峰值达到7.9。这表明在1维光子晶体全反射隧穿峰值处光子晶体内部光场的分布具有周期性，并且光场的分布很强。透射空间光场保持0.97不变。

从前面的对比分析中可以看出，材料的色散对1维光子晶体全反射隧穿的光场分布的周期性和强弱都有明显的影响。

3 结 论

利用特征矩阵的方法推导出光在1维光子晶体中光场的分布公式，利用光场的分布公式和材料的色散公式研究了材料色散对1维光子晶体全反射隧穿光场分布的影响。研究表明：材料色散对1维光子晶体全反射隧穿的光场的分布会产生明显的影响，材料色散会使全反射隧穿光场的峰值发生明显变化，会使光场分布的周期性发生明显改变。这些规律的获得加深了对1维光子晶体全反射隧穿现象的认识。

［1］ WANG R，ZHANG C X，NIE Y H.Band structure and propagation properties of one-dimension anisotropy photonic crystalsl［J］.Acta Photonica Sinica，2007，35（1）：89-92（in Chinese）.

［2］ LIU Q N.The defectmode of electromagnetic wave in flat-panel doping photonic crystal［J］.Laser Technology，2010，34（3）：363-367（in Chinese）.

［3］ LIU Q N.A new simple and convenient method for study of properties forbidden band of one-dimensional photonic crystal［J］.Acta Photonica Sinica，2007，36（6）：1031-1034（in Chinese）.

［4］ LIU Q N.Effect of impurity absorption on one-dimensional photonic crystal defectmode［J］.Chinese Journal of Lasers，2007，34（6）：777-780（in Chinese）.

［5］ LIU Q N.Defect modes of Ag-doped photonic crystal［J］.Semiconductor Optoelectronics，2009，30（5）：702-706（in Chinese）.

［6］ LIU Q N.The defect mode and the quantum effect of light wave in cylindrical anisotropic photonic crystal［J］.Acta Physica Sinica，2011，60（1）：014217（in Chinese）.

［7］ LIU Q N.Design of novel kind of polarization filter on high grade photonic crystal［J］.Piezoelectrics＆Acoustooptics，2010，32（4）：520-523.

［8］ LIU Q N.Themode and bandgap of electromagnetic wave in flatpanel 1-D photonic crystal［J］.Semiconductor Optoelectronics，2010，31（1）：108-111（in Chinese）.

［9］ DAIH X，LIU Q N.Dispersion characteristics of defect mode in 1-D square doped photonic crystal waveguide［J］.Laser Technology，2013，37（3）：338-341（in Chinese）.

［10］ LIU Q N.Polarization and total reflection tunnel effect of flatpanel photonic crystal［J］.Laser Technology，2012，36（1）：114-118（in Chinese）.

［11］ LIU Q N.The mode and bandgap of electromagnetic wave in cylindrical1-D photonic crystal waveguide［J］.Journal of Sichuan Ordnance，2011，32（12）：1-5（in Chinese）.

［12］ LIU Q N.Interference theory of the defect mode in 1-D doped photonic crystal［J］Chinese Journal of Lasers，2013，40（8）：0806001（in Chinese）.

［13］ LIU Q N.Analytical study on the total reflection tunnel effect of 1-D photonic crystal［J］.Acta Optica Sinica，2012，32（2）：193-196（in Chinese）.

［14］ LIU QN，LIUQ.Dispersion characteristics of the total reflection tunnel in 1-D photonic crystal［J］.Acta Photonica Sinica，2013，42（5）：611-615（in Chinese）.

［15］ LIU QN.Field distribution of polarized light of defect mode in 1-D doping photonic crystal［J］.Acta Optica Sinica，2013，33（11）：1116001（in Chinese）.

Effect of dispersion on light field of total reflection tunnel in 1-D photonic crystal

LIU Qineng1，LIU Qin2
（1.School of Computer Science and Information Engineering，Chongqing Technology and Business University，Chongqing 400067，China；2.Institute of Design and Art，Chongqing Technology and Business University，Chongqing 400067，China）

In order to obtain effect of material dispersion on the light field distribution of the total reflection tunnel in 1-D photonic crystal，the light field formula of 1-D photonic crystal was deduced based on the characteristic matrix.The effect of material dispersion on the light field distribution of total reflection tunnel in 1-D photonic crystal was studied by the light field distribution formula and the material dispersion formula.The results show that the dispersion can affect the light field of total reflection tunnel.The dispersion can change the peak of the light field and make obvious change of the periodicity of the light field.The study makes deeper understanding of the phenomenon of the total reflection tunnel of1-D photonic crystal.

optoelectronics；photonic crystal；dispersion；total reflection tunnel；light field

O436.3

A

10.7510／jgjs.issn.1001-3806.2014.06.004

1001-3806（2014）06-0738-04

重庆市教委科技项目基金资助（KJ130713）

刘启能（1957-），男，教授，现主要从事光学与声学的研究。

E-mail：liuqineng57＠163.com

2013-11-04；

2013-12-05