遗传算法的超大跨度充气结构设计优化

杨永强，马云鹏，林 康，武 哲

（北京航空航天大学航空科学与工程学院，100191北京）

遗传算法的超大跨度充气结构设计优化

杨永强，马云鹏，林 康，武 哲

（北京航空航天大学航空科学与工程学院，100191北京）

为了提高超大跨度充气结构设计水平和研发效率，用遗传算法和有限元分析相结合的优化方法进行了超大跨度充气结构设计优化.应用ABAQUS有限元分析软件建立了充气结构有限元模型并进行计算分析，采用遗传算法进行优化，经繁殖和进化后获得最优解.分析结果可知，最优解蒙皮材料应力分布基本均匀，结构各附件平均应力水平较高，具有较高的材料利用率，结构整体质量为3 928 kg.根据最优解进行了样件加工测试，在所有工况下充气结构均可安全工作，旋翼翼梢处最小水平安全距离1.09m，最小垂直安全距离1.67m，与有限元分析结果基本一致.测试结果与分析结果基本一致，优化方案能够满足运用要求，验证了该优化方法是有效的.

充气结构；遗传算法；有限元方法；优化设计

充气结构是轻型空间结构的一个重要分支，通过风机向结构内部输送空气，使充气结构膜材料内外保持一定的压差以保证结构的整体刚度.充气结构与传统建筑结构相比具有建设周期短、建设成本低、质量轻等显著优势［1］，正受到世界各国的普遍关注.

目前欧美军事强国已将充气结构技术广泛应用于军事领域，装备了多种型号的充气式野战医疗帐篷和宿营帐篷.近年来美军根据军用飞机野战机动保障需求而研发了多种型号的野战充气式机库（如图1所示），可为飞机提供机动保障，显著提高了飞机的出勤率，降低了飞机全寿命维修费用.我军目前仍然没有类似的保障装备，因此对于可快速机动保障的野战充气式机库具有强烈的需求.

图1 国外充气机库

军用飞机或直升机的翼展、旋翼直径都较大，一般在10～30 m范围，要确保战机在机库内能够安全停放，对充气式机库的横向跨度和结构刚度有很高的要求.研究超大跨度充气结构，对于为我军大部分主力机型提供野战机库保障具有重要意义.

遗传算法具有通用、并行、稳健、简单与全局优化能力强等突出特点［2］，在风力叶片优化［3］、火箭发动机参数优化［4］等方面已有广泛应用.本文以某型军用直升机为参考进行超大跨度充气结构设计研究，提出合理可行的结构形式，建立超大跨度充气结构模型；并将遗传算法与ABAQUS有限元软件分析相结合，对充气结构进行优化设计，获得优选方案；按照优选方案完成超大跨度充气结构样件加工，并完成相关试验以验证方案的可行性.

1 优化数学模型的确定

式中:X=｛x1，x2，…，xn｝为设计变量，一般为结构的设计尺寸参数；gi（X）为状态变量或约束；f（X）为目标函数；m为约束总数．本文以超大跨度充气结构的优化设计为例，确定该数学模型的各项参数．

1.1 设计变量

野战机库充气结构为半圆拱形多气室结构，其外形如图2所示，由外表面裁片、内表面裁片、侧面裁片、底面裁片和内部拉筋裁片组成，裁片所用材料为高强度膜材料，各裁片之间通过高频热合工艺连接.超大跨度充气结构设计变量包括最大跨度、气肋直径、气室中心间距、充气结构内外压差以及各裁片的厚度共计9个设计变量，各设计变量取值范围如表1所示.

超大跨度充气结构优化属于有约束的结构优化问题，其一般意义上的数学模型为

图2 超大跨度充气结构

表1 设计变量取值范围表

1.2 状态变量

选取直升机旋翼翼梢处的水平和垂直安全距离以及局部最大应力作为状态变量，即优化过程中所产生的每种设计方案所对应的超大跨度充气结构，其旋翼翼梢处的水平和垂直位移应在合理范围内，从而保证直升机能够在机库内安全停放，同时其最大应力应小于材料的许用应力.

如图3所示，为保证直升机安全停放，充气结构变形后的旋翼高度水平安全距离lH和垂直安全距离lV应大于1 m.

图3 旋翼翼梢处水平和垂直安全距离

对于应力约束，通过对不同厚度膜材料进行拉伸断裂强度测试（结果如图4所示）可知在0.5～1.0 mm厚度范围内，膜材料拉伸断裂强度与厚度近似呈线性关系，本文将按照线性关系进行处理，经计算得到该类材料断裂强度σ为71.4 MPa.由文献［5］可知，膜材料的许用应力约为其拉伸断裂强度的1／4，即17.8 MPa.设膜材料在各工况（包括风载、雪载及风雪载组合）分析中所产生的最大局部Von Mises应力为σ1，则优化数学模型中的约束可以表示为

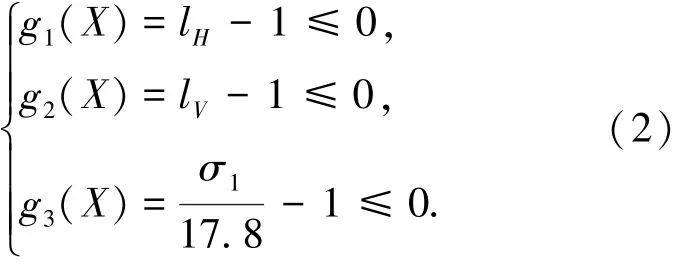
图4 不同厚度膜材料拉伸断裂强度测试结果

1.3 目标函数

对结构进行优化时，通常选取结构总质量或总体积作为目标函数，即优化的目标是使结构在性能满足要求的前提下质量尽量轻，以充分利用材料和节省成本.本文为进一步对结构进行优化，将结构总体积作为目标函数的一项.同时为进一步比较总体积相等或接近的两种设计方案的优劣，将充气结构在各种典型工况下的平均应力水平引入目标函数，通过考核总体积相等设计方案的材料平均应力水平，从中选取平均应力水平较高（即材料利用率高）的方案作为优选方案.由以上分析，选取目标函数的表达式为

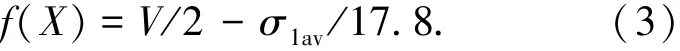
式中:V为充气结构总体积；σ1av为膜材料的平均应力．经估算后的结构总体积约为5 m3，为其赋以1／2缩减系数，即能确保目标函数的有效性，同时也可以保证目标函数具有较高的判断精度.

联立式（1）～（3）即可得到充气结构优化的数学模型为

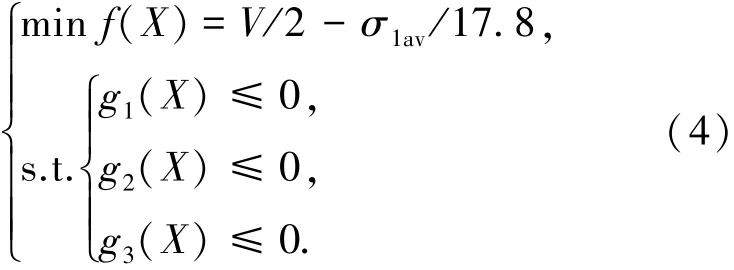
2 优化过程

2.1 受力工况及载荷

野战充气机库所受外部载荷主要是风载荷和雪载荷，受力工况为风载荷、雪载荷以及风雪载荷共同作用工况.

风荷载标准值为［6］

式中:ωk为风荷载标准值，kN／m2；βz为z高度处的风振系数；μz为风压高度变化系数；μs为风荷载体型系数；ω0为基本风压，kN／m2.

以上各系数计算方式参照文献［6］，设计要求野战充气机库可抵抗6级以上风载，则由式（5）计算可得相应风载荷为262.7 Pa.由前期计算分析可知，对于此类拱形结构，如图5所示，侧向风、前后正向风、斜向风载荷差别较大，经前期计算证实最恶劣工况为斜向45°风向.由于野战充气机库作为临时防护装置使用，因此对其抗风能力要求较低，在较小的风载下气动弹性问题可以不予考虑，而仅将风载作为静载荷施加给结构模型.

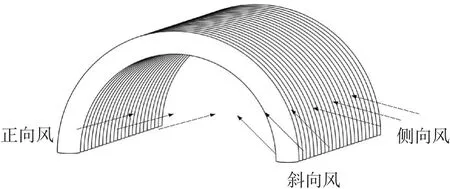
图5 风载荷方向

设计要求野战充气机库可承受300 mm雪载荷，由参照文献［6］可知，雪密度约为100 kg／m3，则计算可得雪载荷约为300 N／m2.

野战充气机库一般通过地锚、沙袋等方式与地面锚固.因此约束载荷为超大跨度充气结构底边所有节点完全固支.

由上述可知，本文充气结构计算分析载荷谱如表2所示.

表2 充气结构计算分析载荷表

2.2 遗传算法编码

本文采用6位二进制数对各变量进行编码，计算可得各变量编码精度（如表3所示）为［7］

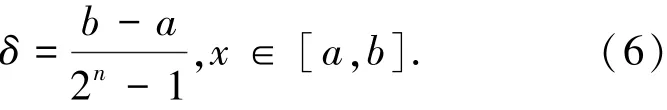
式中:δ为编码精度；［a，b］为设计变量取值范围；n为编码位数．

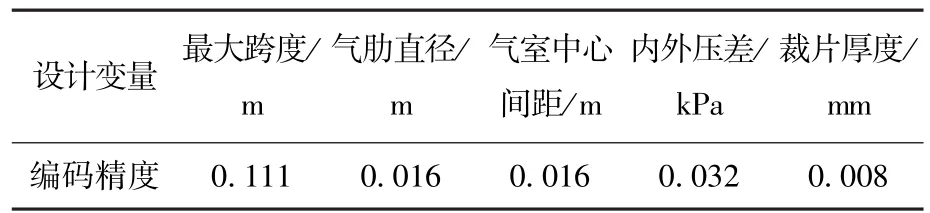
表3 设计变量编码精度

2.3 适应度函数

参考超大跨度充气结构的优化数学模型，采用约束的凝聚处理技术［8］和惩罚策略［9］，确定超大跨度充气结构优化的适应度函数为

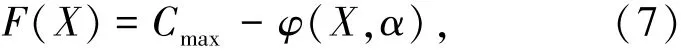
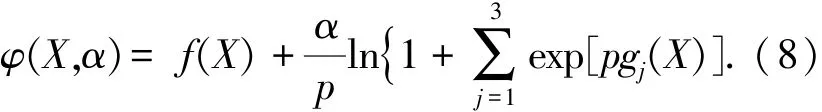
式中:Cmax取当代群体中最大的目标函数值maxφ（X，α）［9］；α为惩罚因子，计算方式见文献［9］；p为控制参数，一般取值104～105．

2.4 优化流程

通过遗传算法和ABAQUS有限元分析软件相结合的方式实现超大跨度充气结构优化.通过遗传算法主程序调用UMAT子程序，可实现根据设计变量进行有限元建模、提取有限元应力应变分析结果等操作.ABAQUS软件是基于Python语言编写的，因此在UMAT子程序中通过编写Python脚本命令即可完成CAE中的所有操作，从而实现参数化建模和数据提取.

编写好的脚本文件提交给ABAQUS的执行过程为:ABAQUS自带的Python解释器解释脚本语言；调用ABAQUS内核执行脚本命令；生成inp输入文件；提交给分析器进行有限元分析；生成结果文件.

运行脚本的途径有:

1）在ABAQUS／CAE主窗口中的最下面有一个命令行接口（CLI），可以在里面输入脚本命令执行，也可以利用命令execfile（′xxx.py′）运行脚本文件；

2）从ABAQUS／CAE主窗口选择菜单File→Run Script运行脚本文件；

3）以命令行方式运行ABAQUS时可以在命令行中指定要运行的脚本文件，例如:abaqus cae script=xxx.py.

采用Python脚本命令建立的充气结构有限元分析模型如图6所示.

图6 充气结构有限元分析模型

优化基本过程如下:

1）定义参数和数组，包括预赋值、设计变量、算法运行参数、循环控制变量等参数和记录算法运行过程中产生的群体、编码和适应度的数组；

2）对设计变量进行染色体编码，确定出个体基因及遗传算法的搜索空间；

3）随机产生初始个体和群体，以其作为初始点开始迭代；

4）对初始群体进行解码操作，并将解码后的设计变量输入UMAT子程序完成充气结构有限元建模；

5）在ABAQUS有限元分析软件中进行各种工况下的计算分析；

6）调用UMAT子程序，提取应力应变、位移、总体积等计算结果并传回算法主程序；

7）将计算结果代入适应度函数计算个体适应度.应用罚函数方法进一步降低不满足设计要求的个体的适应度，提高优良个体的遗传几率；

8）采用比例选择方法筛选个体放入交配池；

9）将交配池中的个体两两配对，采用双点交叉法随机设置交叉点进行基因交换；

10）小概率随机抽取交叉产生的新个体，并同样随机对某个或某些基因位上的基因用其等位基因进行变换；

11）采用无回放余数随机选择方法［10］产生新的群体，并与原群体组合形成扩展群体，提取扩展群体中适应度较高的前半部分作为本次循环的新生群体；

12）判断算法是否收敛或到最大迭代次数要求:是则停止循环并输出优化结果；否则转到第四步继续进行求解.

优化设计流程如图7所示.

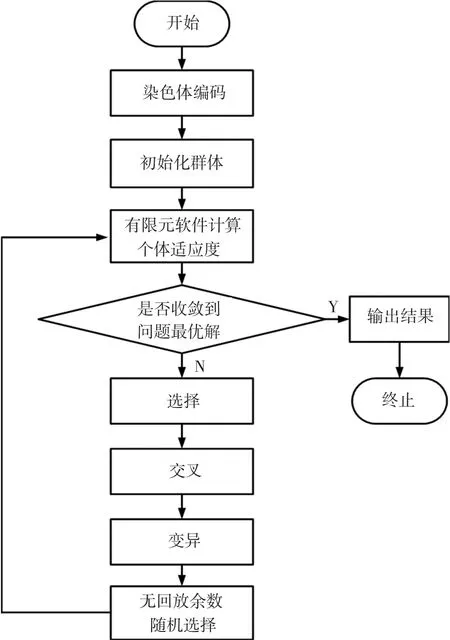
图7 优化设计流程

3 优化结果

应用遗传算法与有限元方法相结合的方式，对超大跨度充气结构进行了优化设计.优化结果显示，初始群体在经过约60代繁殖和进化后已经趋于最优解，经过96代繁殖和进化后收敛于最优解，收敛过程如图8所示.

最优解各设计变量值如表4所示，最优解在典型工况下的有限元分析结果如图9所示，超大跨度充气结构在所有工况下整体结构稳定.

图8 充气结构总体积进化曲线

表4 优化结果各设计变量值

图9 不同工况有限元分析结果

如图9（a）所示，风载荷单独作用下旋翼翼梢处水平安全距离最小，其值为1.18 m；如图9（b）所示，雪载荷单独作用下垂直安全距离最小，其值为1.62 m；最小水平安全距离和最小垂直安全距离均能够满足直升机停放需求.

如图9所示，充气结构膜材料最大局部Von Mises应力出现在风、雪载荷共同作用工况，最大应力区域为充气结构根部，其值为16.9 MPa，小于许用应力，整体结构安全可靠；由应力云图颜色分布可以看出在各工况下蒙皮材料应力分布基本均匀，结构各附件平均应力水平较高，具有较高的材料利用率，结构整体质量为3 928 kg.

4 样件测试

按照优化方案完成了样件加工，样件除长度方向为实际机库尺寸的1／4外，其余尺寸均与优化方案相同，加工完成的样件如图10所示.

将样件与地面锚固后进行样件加载测试，其中风载荷为测试地点的实际风速，雪载荷按照设计要求以模拟载荷的形式施加给样件，测试现场如图11所示.风载荷、雪载荷以及风、雪载荷共同作用工况下的样件变形如图12、13所示，由图可知，在所有工况下充气结构均可安全工作，旋翼翼梢处最小水平安全距离1.09 m，最小垂直安全距离1.67 m，与有限元分析结果基本一致.经样件测试验证了遗传算法与有限元分析相结合的优化方法的可行性，证实了超大跨度充气结构优化方案能够满足设计要求.

图10 按照优化结果加工的充气结构样件

图11 样件加载测试

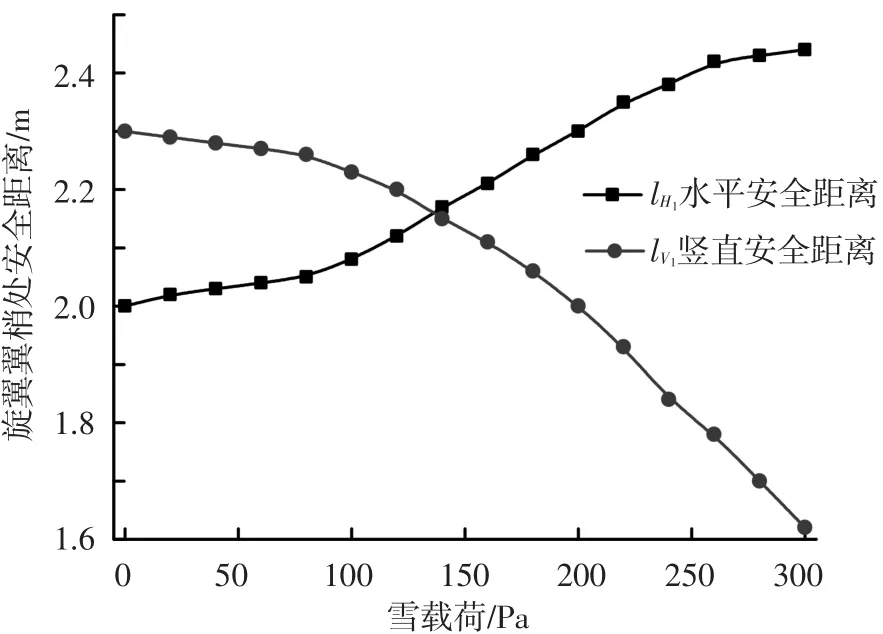
图12 雪载荷作用下的旋翼翼梢处安全距离

图13 风载／风、雪载荷共同作用下的旋翼翼梢处安全距离

5 结 论

1）本文采用遗传算法与有限元分析相结合的优化方法对超大跨度进行优化设计，建立超大跨度充气结构有限元模型，对各种工况下的边界条件和载荷进行处理，应用有限元分析软件ABAQUS进行计算，采用遗传算法进行优化，初始群体经96代繁殖和进化后达到最优解.

2）根据优化方案进行了超大跨度充气结构样件加工，同时进行了多种工况下的样件测试，由测试结果可知，优化方案能够满足设计要求，验证了遗传算法与有限元分析相结合的方法的有效性.

［1］KOCH K M，HABERMANN K J，FORSTER B. Membrane structures:innovative buildingwith film and fabric［M］.New York:Prestel，2004.

［2］玄光男，程润伟.遗传算法与工程设计［M］.北京:科学出版社，2000.

［3］张宇，陈长征，潘萍萍，等.基于遗传算法的风力机叶片优化设计［J］.机械设计与制造，2013，2（13）: 42-44.

［4］何景轩，田维平，何国强，等.基于遗传算法的固体发动机参数优化设计［J］.固体火箭技术，2004，27（4）:250-254.

［5］李阳.建筑膜材料和膜结构的力学性能研究与应用［D］.上海:同济大学，2007:23-24.

［6］中国建筑科学研究院.GB50009—2001建筑结构载荷规范［S］.北京:中国建筑工业出版社，2002.

［7］王小平，曹立明.遗传算法-理论应用与软件实现［M］.西安:西安交通大学出版社，2002.

［8］唐文艳，顾元宪.遗传算法中约束的凝聚选择和复合形处理方法［J］.工程力学，2002，19（6）:58-62.

［9］唐文艳，顾元宪，李云鹏.遗传算法求解可行域分离的结构优化问题［J］.力学学报，2003，35（3）:361-366.［10］周明，孙树栋.遗传算法原理及其应用［M］.北京:国防工业出版社，1999.

（编辑张 红）

An optim izing design method of large span inflatable structure based on genetic algorithm

YANG Yongqiang，MA Yunpeng，LIN Kang，WU Zhe
（School of Aeronautic Science and Engineering，Beihang University，100191 Beijing，China）

To improve the design level and R＆D efficiency of large-span inflatable structure，an optimization method combining FEM with genetic algorithms is applied to design optimization of large span inflatable structure.A FEM model of the inflatable structure is established，calculated and analyzed with the FEM software ABAQUS，then the model is optimized with genetic algorithms and the optimal solution is obtained after breeding and evolution.From the analysis results，there are uniform stress distribution on skin material，higher average stress levels on each accessory structure，a high material utilization and the weight3 928 kg of whole structure in the optimal solution.According to the optimal solution，the sample is processed and tested，and it can safely work under all conditions.The minimum safety distance of rotor wingtip is 1.09 m，and theminimum vertical safety distance is 1.67 m，which are consistent with the results of FEM.The test results are almost consistentwith the analysis，and the optimization program meets the practical requirements well.

inflatable structure；genetic algorithm；finite elementmethod；optimizing-design

V219

A

0367-6234（2014）09-0086-06

2013-08-20.

杨永强（1988—），男，博士后.

马云鹏，myp＠buaa.edu.cn.