基于迭代自组织数据分析算法与蚁群算法建立有机物黏度的QSPR模型

时静洁 陈利平 陈网桦

(南京理工大学化工学院安全工程系,南京210094)

1 引言

结构决定性能是化学中的一条基本规律.定量构效关系(QSPR)方法可以将化合物的结构信息、物理化学参数与化合物的性质进行分析计算,得到表征分子结构的描述符,建立合理的数学模型,发现和确定对有机物的物理化学性质起决定作用的结构因素.1-3目前,已有研究者4-8运用QSPR方法对预测黏度进行了一定的研究.如张莺4采用分子电性距离矢量(MEDV)表征酯分子的结构,分别应用多元线性回归(MLR)和偏最小二乘(PLS)回归进行了线性建模,结果较好,但只适用于酯类液体,涉及到的化合物较少,使用受到限制;而且并未对样本集进行训练集和测试集划分,所得结果有待验证.Gharagheizi5对聚合物溶液黏度进行了QSPR研究,分别建立了遗传算法与多元线性回归(GA-MLR)模型和径向基函数神经网络(RBFNN)模型,其结果令人满意,但该研究并未对所建立的模型进行全面的评价与验证,且模型仅适用于聚合物溶液,使用范围较窄.

针对以上一些局限性,本文进行了一些改进.在对样本集进行初步分类的基础上,再对训练集和测试集进行划分,这也是本文的创新点之一.由于样本中一些化合物结构比较复杂,且有些化合物同时属于几个类别,很难将其分类,因此采用了具有试探性和人机交互功能的动态聚类算法——迭代自组织的数据分析法(ISODATA)对其进行分类.本文采用蚁群优化算法(ACO)对分子描述符进行筛选,且分别与多元线性回归法和支持向量机法组合建立预测黏度的模型,并对所建立的模型进行了机理解释.此外,本文还对所建立的模型进行了比较全面的评价与验证,对模型的应用域做了一定的研究.

2 样本与方法

2.1 分子描述符的计算

分子描述符是建立QSPR模型的基础.分子描述符是用逻辑和数学程序将分子结构中的化学信息转化成数值的符号表征.本文首先借助化学软件Hyperchem7.5进行分子结构的输入,随后采用分子力学方法MM+进行初步优化,用量子化学半经验方法PM3进行进一步几何优化,所有计算都限制在Hartree-Fock能级,采用Polar-Ribiere方法直至RMS梯度达到0.41868 kJ·mol-1,最后获得能量最低的稳定构型.将优化好的分子结构导入DRAGON2.1软件计算分子描述符,其中包括组成描述符、拓扑描述符、几何描述符、电性描述符等18类共1481种分子描述符.

2.2 ISODATA算法

ISODATA算法是一种常用的动态聚类划分算法.目前,ISODATA算法在油水层判别问题,9原油开发中判断漏失层的存在以及漏失层的位置,10复杂体制雷达信号分选,11网络路由选择算法12等方面得到了很好的应用.鉴于ISODATA算法的上述优点,本文提出基于ISODATA算法对样本集进行初步分类.

ISODATA主要算法思想是首先根据最小距离准则获得初始聚类,然后判断初始聚类结果是否符合要求.若不符,则将聚类集进行分裂和合并处理,得到新的聚类中心,再判断聚类结果是否符合要求.如此反复迭代直到完成聚类划分操作.ISODATA算法步骤13如下:(1)设置聚类分析控制参数是ISODATA的关键步骤,主要包括:期望得到的聚类数K;一个聚类中的最少样本数θN,如小于此数就不作为一个独立的聚类;一个聚类域中样本距离分布的标准差θS;θC是两聚类中心之间的最小距离,若小于此数,合并两个聚类;一次迭代运算中可以合并的聚类中心的最多对数L;允许迭代的代数为I.(2)初始分类,读入准备分类的N个模式样本(Xi,i=1,2,…,N),预选Nc个样品作为初始聚类中心,根据最小距离准则将各样本分类.(3-5)按控制参数给定的要求,将前一次获得的聚类集进行分裂和合并处理,以获得新的聚类中心和分类集(其中(4)为分裂处理,(5)为合并处理).(6)再次迭代运算,重新计算各项指标,判别聚类结果是否符合要求,以此反复经过多次迭代运算,直至得到理想的聚类结果.

2.3 样本集的确定

由于黏度受温度等因素影响较大,因此本文选用了310种有机物在25°C的液体黏度作为研究样本,并将所有的黏度值取自然对数(用lnη表示)作为模型的因变量.可靠的QSPR预测模型必须以可靠的实验样本为基础,因此为了最大程度地消除实验数据之间的差异可能给预测模型所带来的影响,本研究选用权威数据库《有机化合物实验物性数据手册》14作为实验样本来源,以确保实验数据的准确性和权威性.

随后,本文并未对样本集进行直接划分.应用ISODATA算法对计算出的所有化合物描述符进行聚类分析,再在每个类别中随机选择样本作为训练集和测试集,训练集和测试集中均涵盖了每个类别的化合物,避免训练集中缺失测试集中的部分信息,使得模型预测能力受到影响.本文选择253个物质作为训练集,用于变量选择和建立模型,57个物质作为测试集,用于外部验证.

2.4 分子描述符的确定

大量的分子描述符中存在冗余信息,故首先利用DRAGON2.1软件的筛选功能进行初步筛选,筛除取值为常数或者近似常数的描述符以及相关系数达到0.95以上的描述符.经过预先筛选,描述符的数目得到了一定程度的降低,减少至628个分子描述符(见表S1,Supporting Information),但仍无法满足QSPR建模的需要.蚁群优化算法(ACO)作为一种新兴的种群智能优化算法,已经在离散的组合优化等问题中被证明是一种高效的变量选择方法.而参数选择问题正属于离散的组合优化问题.因此,我们将蚁群优化算法用于分子描述符参数的变量筛选,以期取得良好的效果.作为一种全局搜索算法,蚁群算法能够有效地避免局部极优.15因此采用蚁群算法进一步筛选,最终确定5个描述符作为模型的输入.

3 结果与讨论

3.1 样本集的划分

运用MATLAB语言来实现ISODATA算法,其主要思路是,把类的分裂合并操作看成是一种二维数组中行矢量位置移动的过程,每一个样本作为数组中的一个行矢量,而每一行的每一列都是样本的属性值,使用MATLAB的矩阵运算可以完成对样本位置的调整,从而模拟对类的调整,最终达到聚类分析的结果.16本文向量的行数310为化合物数,列数628为属性值,即预筛选后的分子描述符数.ISODATA算法部分参数设置为:K=8,θN=3,θS=1,θC=2,L=10,I=20.基于ISODATA算法聚类分析对化合物的分类如表1所示,类中心间的距离如表2所示.

表1和表2中的距离均为欧氏距离,欧氏距离是最易于理解的一种距离计算方法,源自欧氏空间中两点间距离公式.两个n维向量a(x11,x12,…,x1n)与b(x21,x22,…,x2n)间的欧氏距离:由表1可以看出,每一类化合物与相应的类中心距离比较小,说明每一类化合物的相似度比较高.由表2可以看出,类中心间的距离均比较大,说明类与类之间差异度比较大.完成对化合物的初步分类之后再从每个类中随机选择样本划分训练集和测试集,其结果见表S2(Supporting Information).

3.2 描述符的筛选结果

运用蚁群算法对DRAGON2.1软件初步筛选后的628个分子描述符进行进一步筛选,其过程是在VC++6.0中采用C语言编程实现.将蚂蚁数量设为500,挥发率设为0.9.进行不断迭代直至收敛,最后筛选出5个分子描述符,分别为 G3u、Hy、H1p、R5m、X3sol.G3u属于WHIM(权重整体不变分子指数)描述符,G3u定义为第三成分对称定向WHIM指数,主要表征分子的结构对称性.Hy是一个与化合物亲水性相关的简单经验指数,它是通过有关亲水性官能团的函数获得,主要反映该分子的亲水性特征.H1p属于GETAWAY(Geometry,Topology and Atom-Weights Assembly,几何、拓扑和原子权重组合)描述符,以原子极化率作为加权性质计算得到的参数,用来反映相邻原子之间原子极化率的相互关系.R5m也是GETAWAY描述符,它根据杠杆矩阵单元计算而得,该杠杆矩阵通过面心原子坐标获得.该描述符主要表征原子量的分布.X3sol为拓扑描述符,由分子图论获得,是一种溶解连接性指数.175个分子描述符相关性分析如表3所示.

相关系数大于0称为正相关,否则为负相关.相关系数绝对值越大,则相关性越强.从表3中可看出其相关系数均小于0.8,这说明参数之间不存在共线性问题,可作为建模的输入参数.18

3.3 ACO-MLR模型

针对训练集样本,以ACO筛选的5个描述符作为输入参数,应用SPSS软件中的多元线性回归(MLR)模块,得到了MLR预测模型,结果如下:

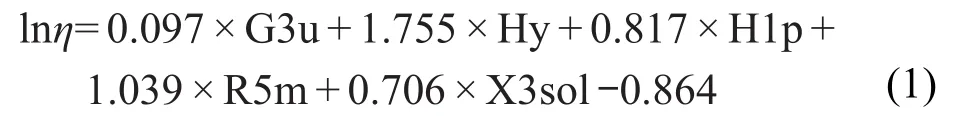
式中lnη为黏度自然对数值.MLR模型的性能参数见表4,表中R2为复相关系数,为“留一法”交互内部验证的复相关系数,为交互外部验证的复相关系数,为模型外部预测能力的验证系数,一致性相关系数(CCC)为模型调和系数,RMSE为均方根误差,n为样本数.方程中,回归系数为正,表明此描述符与黏度值正相关,反之,回归系数为负则为负相关,且系数越大,相关程度越高.由此得出,在此模型中,各描述符与黏度的相关性大小顺序依次为:Hy、R5m、H1p、X3sol、G3u.根据各描述符回归系数的正负号和大小可知,Hy越大,即分子中所含亲水基团越多,亲水性越强,则黏度越大;R5m越大,即分子量越大,则黏度也越大;H1p越大,即相邻原子之间原子极化率越强,则黏度也越大;X3sol越大,即分子中的溶解连接性指数越大,则黏度也越大;而G3u指的是分子的结构对称性,其前面的系数最小,相关性最低,说明它对黏度的影响最小.ACO-MLR模型对训练集和测试集的实验值和预测值的结果见表S2.

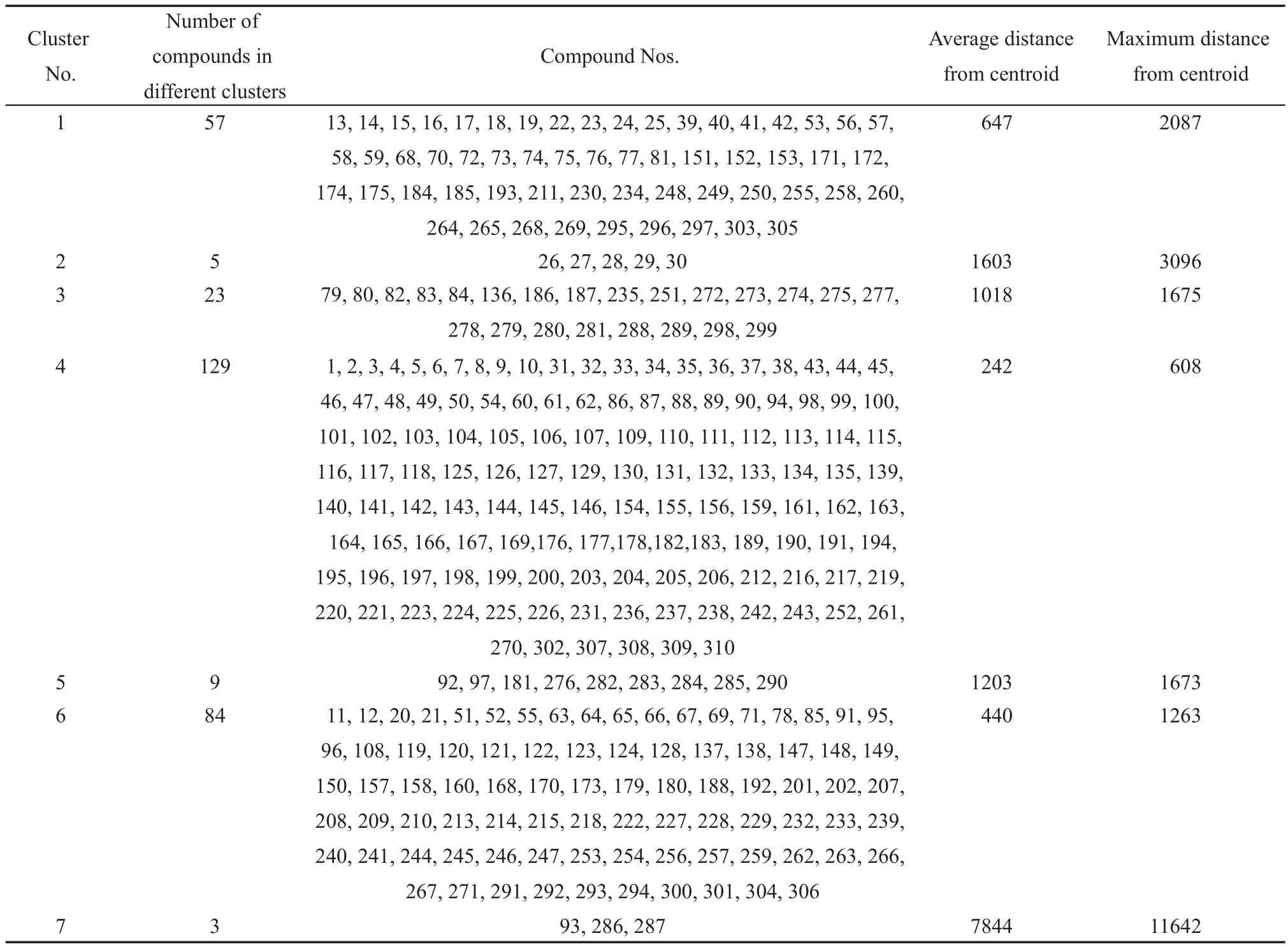
表1 基于ISODATA算法聚类分析对化合物的分类Table 1 Classification of compounds based on ISODATAclustering analysis

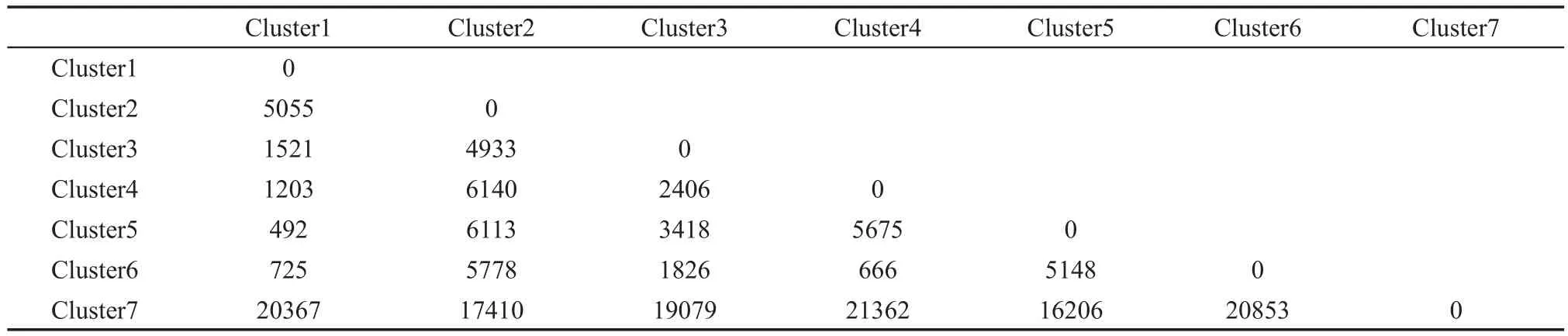
表2 类中心间的距离Table 2 Distances among cluster centroids

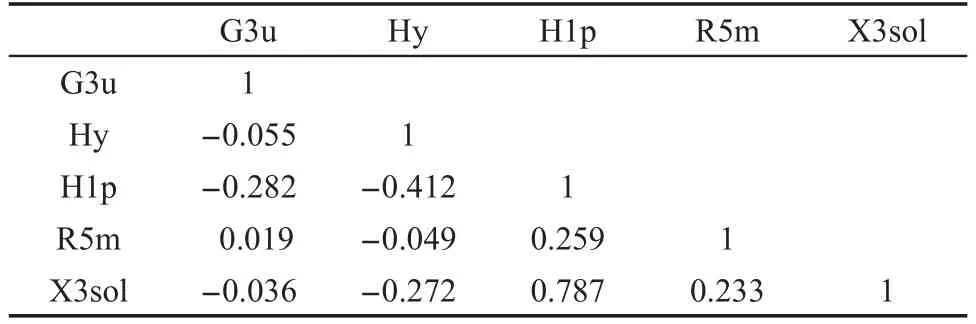
表3 分子描述符相关系数Table3 Correlation coefficients of molecular descriptors

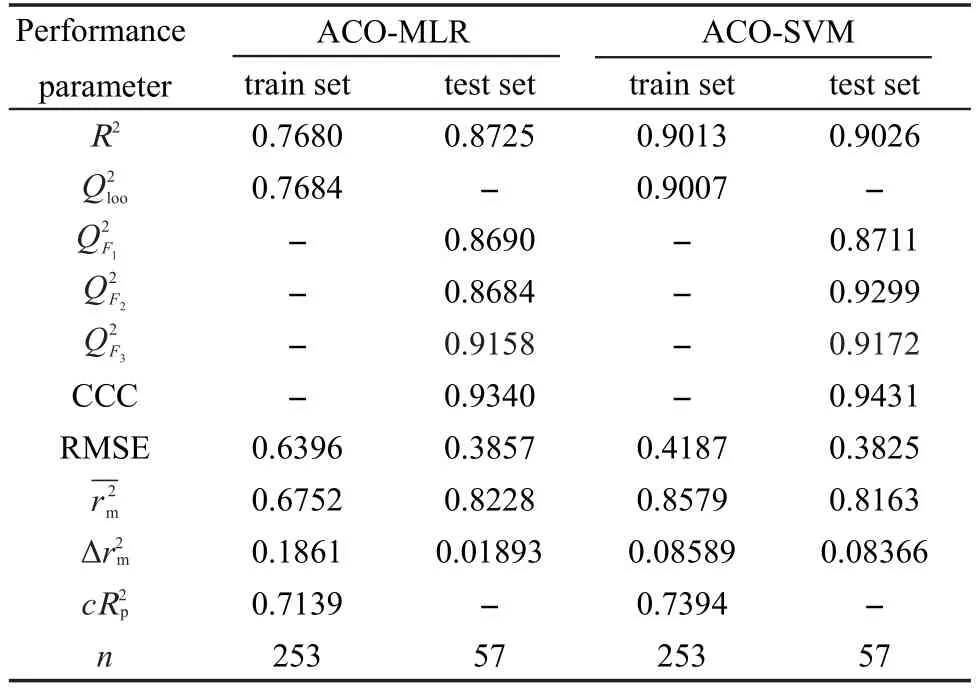
表4 ACO-MLR和ACO-SVM模型的主要性能参数对比Table4 Performance parameter comparison between ACO-MLR andACO-SVM models

随后,对测试集样本的黏度进行预测,以验证模型的外部预测能力.ACO-MLR模型所得的黏度预测值与实验值的相关系数为0.934,其预测值与实验值的比较见图1.

3.4 ACO-SVM模型

随后,为了进一步对黏度与分子结构间可能存在的非线性关系进行研究,并获得性能更优的预测模型,本文以MLR模型所选择的分子描述符作为输入变量,以黏度自然对数值作为输出变量,应用非线性的支持向量机(SVM)方法建立新的QSPR模型.用SVM做预测时,相关参数(主要是惩罚参数C和核函数参数γ)的选择是个难点,参数选择不好,将会严重影响预测的精度和准确率.

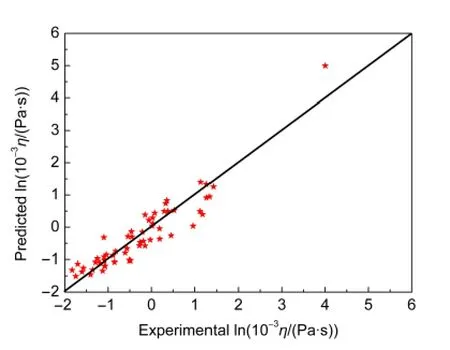
图1 ACO-MLR模型对测试集所得预测值与实验值的比较Fig.1 Comparison between the predicted and experimental values byACO-MLR for test set

为了得到适合的相关参数,选择了应用最为广泛的径向基函数(RBF)作为核函数,采用格点搜索(GS)的方法来选择最佳的参数组合.惩罚系数C和RBF核函数的宽度γ的搜索范围为[2-8,28],步长为1,并根据对训练集进行“留一法”交互验证所得的来确定最佳的模型参数.最终选择的最优参数为:惩罚系数C=64,核函数的宽度γ=1.4142,不敏感损失函数ε=0.1.ACO-MLR模型对训练集和测试集的实验值和预测值的结果见附表S2.所得的SVM模型的主要性能参数见表4,ACO-SVM模型所得的黏度预测值与实验值的相关系数为0.950,其预测值与实验值的比较见图2.

3.5 结果比较与分析

从图1和图2中可以看出,ACO-MLR模型和ACO-SVM模型对测试集中57个样本的预测值均与实验值有较好的一致性,预测精度令人满意.比较模型中训练集和测试集的预测结果发现,各子集的复相关系数均比较高,预测误差较低,而且比较接近.一般认为,若均大于0.6,CCC大于0.85,19,20则说明所建立的模型不但比较稳定,而且具备较强的预测能力和泛化推广性能.

充分评价一个模型的预测能力,针对测试集必须要满足以下三个条件:21(1)复相关系数R2大于0.6;(2)为实验值与预测值的相关系数的平方;(3)通过原点的回归线斜率k和k′在0.85和1.15之间.由表4可知,测试集的复相关系数R2均大于0.6.ACO-MLR模型中,测试集的0.8724,模型中,测试集的两模型的值均远远小于0.1.通过拟合可得ACOMLR模型的k=0.9313,k′=0.9445,ACO-SVM模型的k=1.0646,k′=0.8513.计算结果表明,两模型通过原点的回归线斜率k和k'均在0.85和1.15之间.

图2 ACO-SVM模型对测试集所得预测值与实验值的比较Fig.2 Comparison between the predicted and experimental value byACO-SVM for test set

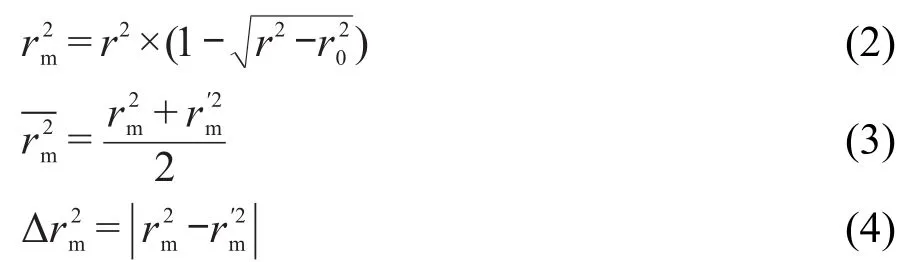
式中,r2是实验值与预测值的回归线斜率,为交换横纵坐标后实验值与预测值的回归线斜率,其回归线均需通过原点.是实验值为纵坐标时所计算的值,而是实验值为横坐标时所计算的值.计算式如式(5)所示：

随后,本文对ACO-MLR模型和ACO-SVM模型的样本集进行了残差分析,讨论模型在建立过程中是否有系统误差产生,两个模型的残差图分别见图3和图4.由图3和图4可以看出,各模型的计算残差均随机分布于基准线的两侧,不存在明显的规律性.由此可以推断,两个预测模型在建立过程中未产生系统误差.

为检验所建模型是否存在机会相关,本文将“Y-随机性检验”方法针对ACO-MLR和ACO-SVM模型分别运行50次.对于ACO-MLR模型所得最大R2为0.3360,ACO-SVM模型为0.7196,其结果均不如原始模型.由此可见,本文所建立的预测模型不存在“偶然相关”现象,具备较强的稳定性.

用Williams图表征模型的应用域(AD).当化合物的标准残差落在(-3,+3)以外时,认为其实验值为离群点;当化合物的臂比值(Hat(hi))大于警戒值(h*)时,认为化合物显著影响模型的回归效果.27

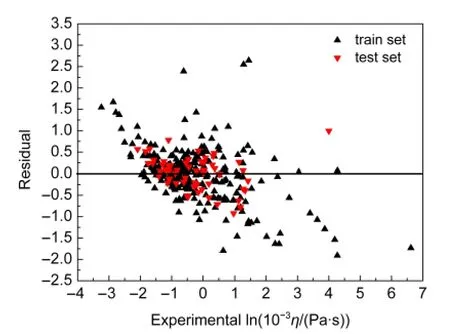
图3 ACO-MLR模型预测值残差与黏度实验值lnη关系图Fig.3 Plot of the residuals of prediction values versus the experimental lnη values forACO-MLR model

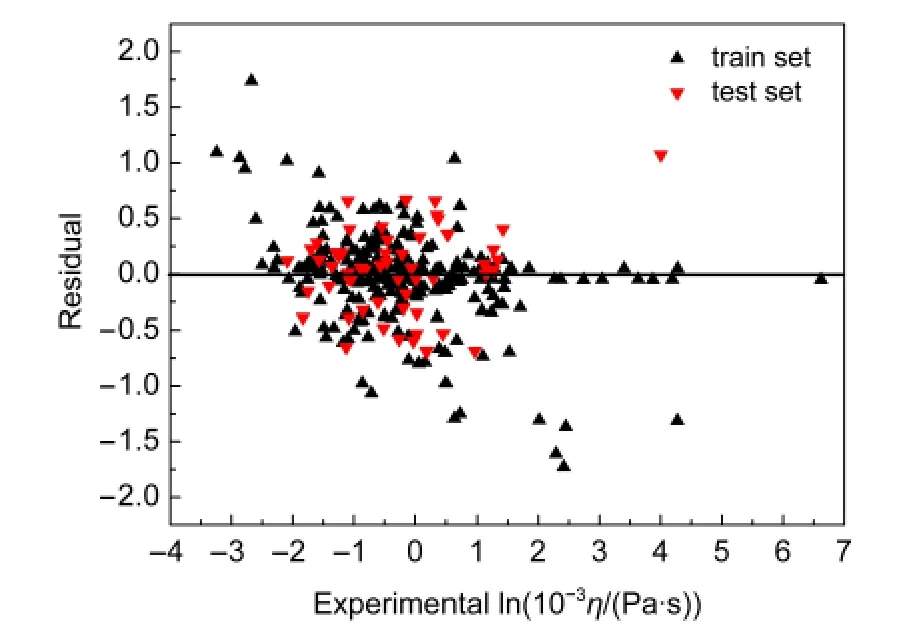
图4 ACO-SVM模型预测值残差与黏度实验值lnη关系图Fig.4 Plot of the residuals of prediction values versus the experimental lnη values forACO-SVM model

由图5和图6可以看出,在ACO-MLR和ACOSVM模型中,测试集中没有出现“异常值”物质.在训练集中,ACO-MLR模型和ACO-SVM模型分别有四个物质和七个物质的标准残差落在了(-3,+3)以外.ACO-MLR模型中的四个物质分别是叔丁醇、二丙酮醇、甲醇、1,4-丁二醇.ACO-SVM模型中的七个物质分别是1,1,1-三氟乙烷、1-癸醇、1-壬醇、3-甲酚、1,4-丁二醇、1-辛醇、三溴甲烷.这些物质的实验值可能出现了比较大的偏差,被称为“异常值”.除此以外,两模型中十氟丁烷、甘油、邻苯二甲酸双(2-乙基己基)酯)、邻苯二甲酸二辛酯,这四个物质的臂比值hi均超过了警戒值h*,可能有两种原因造成.第一是这些分子的某些结构特征并未被所筛选出的分子描述符很好表征;第二是这些分子的某些结构对于整个样本集来说比较特别.

十氟丁烷、甘油、邻苯二甲酸二辛酯是训练集样本中的,这些物质影响变量筛选,进而影响所建立模型的质量.测试集中只有邻苯二甲酸双(2-乙基己基)酯的hi值超过了警戒值h*,说明模型对此化合物的预测结果可能是不可靠的,它的预测结果可以被认为是由模型外推出来的.

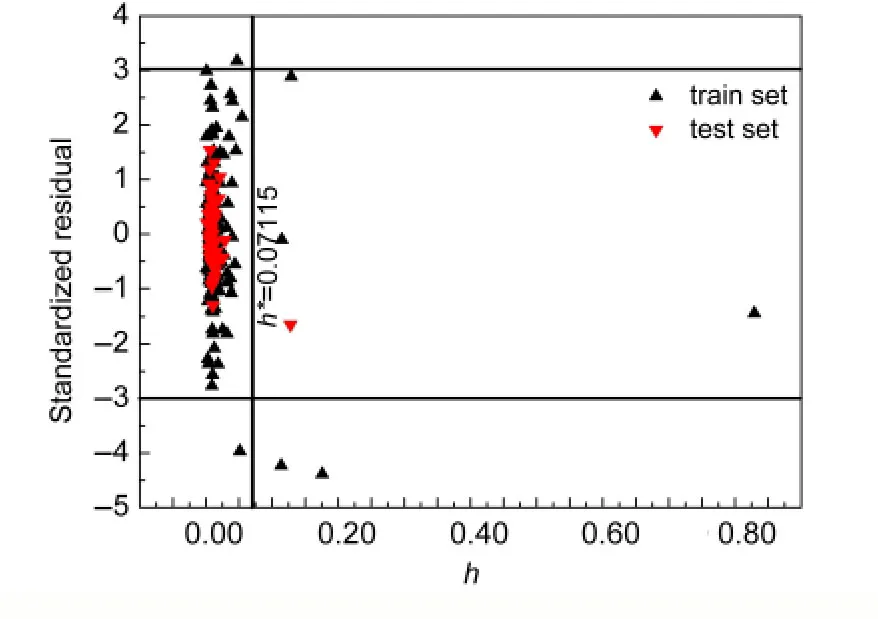
图5 ACO-MLR模型训练集和测试集的Williams图Fig.5 Williams plot of theACO-MLR model for the train and test sets

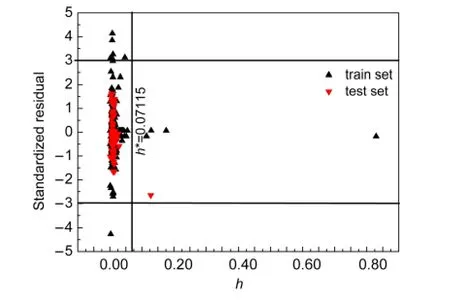
图6 ACO-SVM模型训练集和测试集的Williams图Fig.6 Williams plot of theACO-SVM model for the train and test sets

4 结论

运用迭代自组织数据分析技术(ISODATA)对样本集进行初步分类,以避免模型中部分类别的缺失.随后本文以蚁群算法(ACO)作为分子描述符筛选方法,分别与多元线性回归(MLR)和支持向量机(SVM)进行组合建立了蚁群-多元线性回归模型(ACO-MLR)与蚁群-支持向量机模型(ACO-SVM),对310个有机化合物的黏度进行了QSPR研究.其中,以ACO-SVM模型为最佳,揭示了有机化合物黏度与其分子结构间可能有较强的非线性关系,也说明了将SVM用于研究QSPR的优越性,它能有效地解决小样本、非线性、过拟合、维数灾难和局部极小等问题,泛化推广的性能也较强.

本文所建立的2个黏度QSPR模型的预测值与实验值非常接近,其结果令人满意,模型性能参数均在可接受范围之内,所建模型稳定且可用于预测黏度.本文的研究为预测有机化合物的黏度提供了一种新的有效的方法,对于化工安全设计和风险评价研究具有重要的意义.

Supporting Information:Molecular descriptors after a preliminary screening have been included in Table S1 and experimental and predicted values of the compound viscosity by ACO-MLR and ACO-SVM have been included in Table S2.This information is available free of chargeviathe internet at http://www.whxb.pku.edu.cn.

(1) Shi,J.J.;Chen,L.P.;Chen,W.H.;Shi,N.;Yang,H.;Xu,W.Acta Phys.-Chim.Sin.2012,28,2790.[时静洁,陈利平,陈网桦,石 宁,杨 惠,徐 伟.物理化学学报,2012,28,2790.]doi:10.3866/PKU.WHXB201209273

(2) Shi,J.J.;Chen,L.P.;Chen,W.H.J.Chemom.2013,27,251.

(3)Han,C.;Yu,G.R.;Wen,L.;Zhao,D.C.;Asumana,C.;Chen,X.C.Fluid Phase Equilib.2011,300,95.doi:10.1016/j.fluid.2010.10.021

(4)Zhang,Y.Comput.Appl.Chem.2013,30,195.[张 莺.计算机与应用化学,2013,30,195.]

(5) Gharagheizi,F.Comput.Mater.Sci.2007,40,159.doi:10.1016/j.commatsci.2006.11.010

(6)Chen,B.K.;Liang,M.J.;Wu,T.Y.;Wang,H.P.Fluid Phase Equilib.2013,350,37.

(7) Gharagheizi,F.;Mirkhani,S.A.;Keshavarz,M.H.;Farahani,N.;Tumba,K.J.Taiwan Inst.Chem.E2013,44,359.doi:10.1016/j.jtice.2012.12.015

(8)Tochigi,K.;Yamamoto,H.J.Phys.Chem.C2007,111,15989.doi:10.1021/jp073839a

(9)Feng,Y.L.;Yi,S.Q.;Feng,Z.L.;Yu,Z.G.;Xu,S.H.Pet.Geol.Oilfield Dev.in Daqing2005,24,87.[冯亚丽,伊三泉,冯卓利,于志刚,许少华.大庆石油地质与开发,2005,24,87.]

(10) Wang,S.L.;Jiang,H.Q.Transp.Porous.Med.2011,86,483.doi:10.1007/s11242-010-9634-4

(11) Zhang,H.L.;Yang,C.Z.Electro.Warfare Technol.2010,25,34.[张洪亮,杨承志.电子信息对抗技术,2010,25,34.]

(12) Ma,Y.;Tan,Z.H.;Chang,G.R.;Wang,X.Y.Procedia Eng.2011,15,2966.doi:10.1016/j.proeng.2011.08.558

(13)Yang,X.M.;Luo,Y.Mining Technol.2006,6,67.[杨小明,罗 云.采矿技术,2006,6,67.]

(14) Ma,P.S.Data Manual for the Physical Property of Organic Compounds;Chemical Industry Press:Beijing,2006.[马沛生.有机化合物实验物性数据手册.北京:化学工业出版社,2006.]

(15) Li,S.Y.;Chen,Y.Q.;Li,Y.Ant Colony Algorithms with Application;Institute of Technology Press:Harbin,2004.[李士勇,陈永强,李 妍.蚁群算法及其应用.哈尔滨:哈尔滨工业大学出版社,2004.]

(16) Li,Y.P.;Li,Y.L.Mining Res.Dev.2005,25,79.[李元萍,李元良.矿业研究与开发,2005,25,79.]

(17) Todeschini,R.;Consonni,V.Handbook of Molecular Descriptors;Wileyt-VCH:Weinheim,2000.

(18)Zhang,Y.M.;Yang,X.S.;Sun,C.;Wang,L.S.Sci.China Chem.2011,41,893.[张一鸣,杨旭曙,孙 成,王连生.中国科学:化学,2011,41,893.]

(19) Chirico,N.;Gramatica,P.J.Chem.Inf.Model.2011,51,2320.doi:10.1021/ci200211n

(20) Chirico,N.;Gramatica P.J.Chem.Inf.Model.2012,52,2044.doi:10.1021/ci300084j

(21)Tropsha,A.;Gramatica,P.;Gombar,V.K.QSAR Comb.Sci.2003,22,69.

(22) Roy,K.;Matra,I.;Kar,S.;Ojha,P.K.;Das,R.N.;Kabir,H.J.Chem.Inf.Model.2011,52,396.

(23)Ojha,O.K.;Mitra,I.;Das,R.N.;Roy,K.Chemom.Intell.Lab.Syst.2011,107,194.doi:10.1016/j.chemolab.2011.03.011

(24) Roy,K.;Chakraborty,P.;Mitra,I.;Ojha,P.K.;Kar,S.;Das,R.N.J.Comput.Chem.2013,34,1071.doi:10.1002/jcc.23231

(25) Mitra,I.;Saha,A.;Roy,K.Mol.Simul.2010,36,1067.doi:10.1080/08927022.2010.503326

(26) Roy,P.P.;Paul,S.;Mitra,I.;Roy,K.Molecules2009,14,1660.doi:10.3390/molecules14051660

(27) Gu,Y.L.;Fei,Z.H.;Zhang,Y.Y.J.Anal.Sci.2012,28,333.[顾云兰,费正皓,张玉莹.分析科学学报,2012,28,333.]doi:10.2116/analsci.28.333