一类单自由度碰撞振动系统的颤振分析

王小斌，周 鹏，黄 剑

(1．数理与软件工程学院；2．机电工程学院，兰州交通大学，甘肃兰州 730070)

一类单自由度碰撞振动系统的颤振分析

王小斌1，周 鹏2，黄 剑1

(1．数理与软件工程学院；2．机电工程学院，兰州交通大学，甘肃兰州 730070)

研究了一类单自由度碰撞振动系统的颤振运动，运用理论推导的方法找到了其颤振完成点及颤振时间，并针对该碰撞系统中的颤振导致的碰撞问题，借助慧尾映射找到了一种有效的研究该碰撞系统中颤振现象的数值方法．利用数值仿真的方法揭示了系统中的完全颤振和不完全颤振现象．

碰撞；颤振；慧尾映射；数值仿真

碰撞问题大量地出现在生物系统和机械系统中，这些系统大多数是非光滑或分段光滑的．非光滑动力系统作为动力学的一个分支，广泛存在于多个科学领域．早期，Steven Wayne Shaw等[1]对碰撞振子作了大量研究，他们发现这类系统中存在倍周期分岔和混沌等非线性特征，随后许多学者将非光滑系统的研究重点由局部分析转向全局问题，也取得了许多成果[2-6]．

碰撞系统通常存在擦边和颤振这两种新颖的非光滑系统的动力学特性，这使得其呈现出许多光滑系统中所没有的复杂动力学行为．颤振作为碰撞系统的一个特殊性质，主要可以概括为完全颤振和非完全颤振．完全颤振表示在有限时间间隔内系统发生了无穷次的碰撞；不完全颤振表示在有限时间间隔内系统发生N（N为一个很大的有限数）次碰撞．本文对一类具有单侧刚性约束的单自由度碰撞振动系统的碰撞过程进行了研究，利用数学理论的相关知识找到了其颤振完成点和颤振时间，并以此碰撞系统为模型（图1），通过借助慧尾映射的概念，有效地近似了完全颤振中产生的碰撞现象，分析了其发生机理．

1 系统的力学模型及运动微分方程

具有单侧刚性约束的单自由度碰撞振动系统的力学模型如图1所示，质量为M的振子由刚度为K的线性弹簧和阻尼系数为C的线性阻尼器连接于支承，并受到简谐激励Psin(ΩT+τ)的水平方向的作用，当振子的位移X等于间隙B时，振子与刚性约束A发生碰撞．

设碰撞由碰撞恢复系数R确定，振幅为P，频率为Ω，相位为τ．当X＜B时，系统自由运动微分方程如下：

当X=B时，碰撞发生，碰撞块的速度根据碰撞法则改变，质块的碰撞方程为：

取无量纲参数：

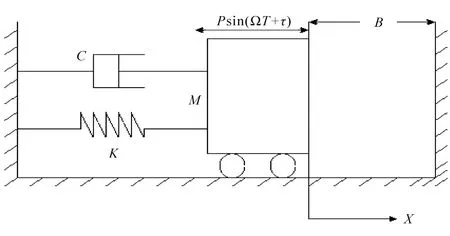
图1 系统模型图

2 碰撞运动

事实上，黏滑运动与系统的颤振有着密不可分的关系．下面来具体分析系统的碰撞运动过程．

其中Ο(1)表明了x的边界函数．若仅仅只保留前两项，可以发现最终的速度恰好为零，相应的发生颤振的时间也是准确的，从x1=0出发，可以发现最终的位置是关于x22阶的，这一点当然是符合忽略项的．由（6）式可知，所有方程定义的函数都是封闭可解的．碰撞是首先发生在∑1-的一个点，通过给定的映射R，视碰撞速度v不依赖于x，依文献[7]可定义第一次碰撞的位置和速度分别为：

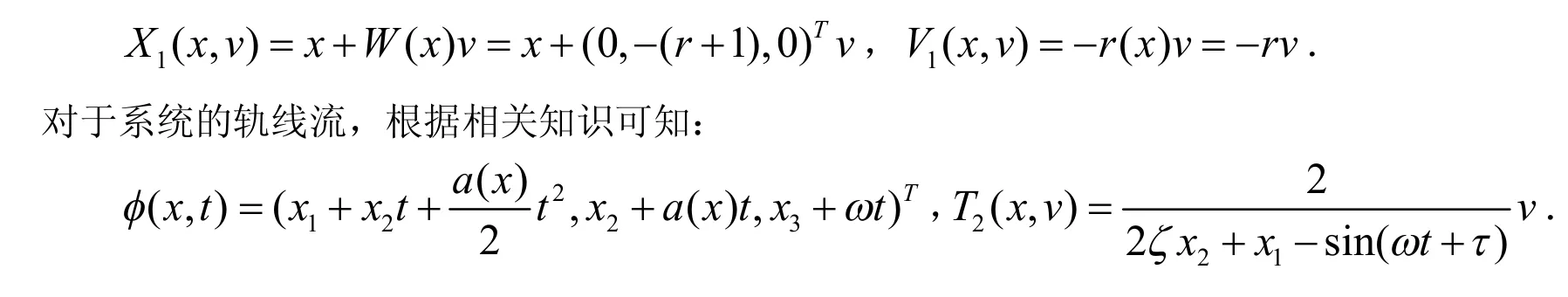
3 数值分析

下面定义一个完全颤振子空间：

取完全颤振子空间中的初始点x0∈∑c，先经过碰撞映射R(x)到达碰撞面的某一点x01，接着自由运动到下一个碰撞点x1，如此反复碰撞，最终到达完全颤振的结束点x*，满足条件：

固定系统参数ζ=0.1，b=0.1，ω=2.7994，r=0.8，初始条件为(0.1,-0.2,0)T，图2（a）为系统P(∞,1)运动的相图（符号P(m,n)表示n个周期中发生m次碰撞）．图2（b）为系统的时间历程图，它给出了从完全颤振到粘滑的过程（图中实线为x2关于t的变化曲线，虚线为x1关于t的变化曲线，m和n分别为粘滑的开始点和结束点）．图2（c）和图2（d）为图2（b）的局部放大图，它展示了完全颤振中的彗尾映射[8]S:m→n．系统的颤振完成点为x1=0.1，x2=0，时间为t=26.667，与前面的理论分析吻合，这验证了理论推导的正确性．

图2 系统((4)式和(5)式)的完全颤振到粘滑运动的彗尾映射

考虑系统的向量场（7），取系统参数ω=2.787，其余参数均同于上图，令恢复系数r依次为0.800、0.801、0.802、0.803、0.803 04、0.803 1．图3（a）–（f）为系统的时间位移图像，展示了系统由非完全颤振到完全颤振再到非完全颤振的过程．从图3（d）和图3（e）可知，当恢复系数r取0.803 – 0.803 04时，系统有一个稳定的完全颤振周期1轨道，从这两幅图中可以明显看到，完全颤振包含有非零时间的黏滑运动，即s＞0．随着恢复系数r值的增大，黏滑运动时间s将减少直到最终对于某个恢复系数值r*有s=0，此时意味着完全颤振将转变为非完全颤振，r*为系统从完全颤振到不完全颤振的参数分岔点，它是以黏滑运动的突然产生和消失作为标准的．更精确地说，在r*处的轨道存在一个点，这个点是无限次碰撞的结束点，因此无黏滑运动产生．图3中（a）、（b）、（c）、（f）的一部分轨迹描绘了这种碰撞次数有限、但值很大的特殊碰撞．

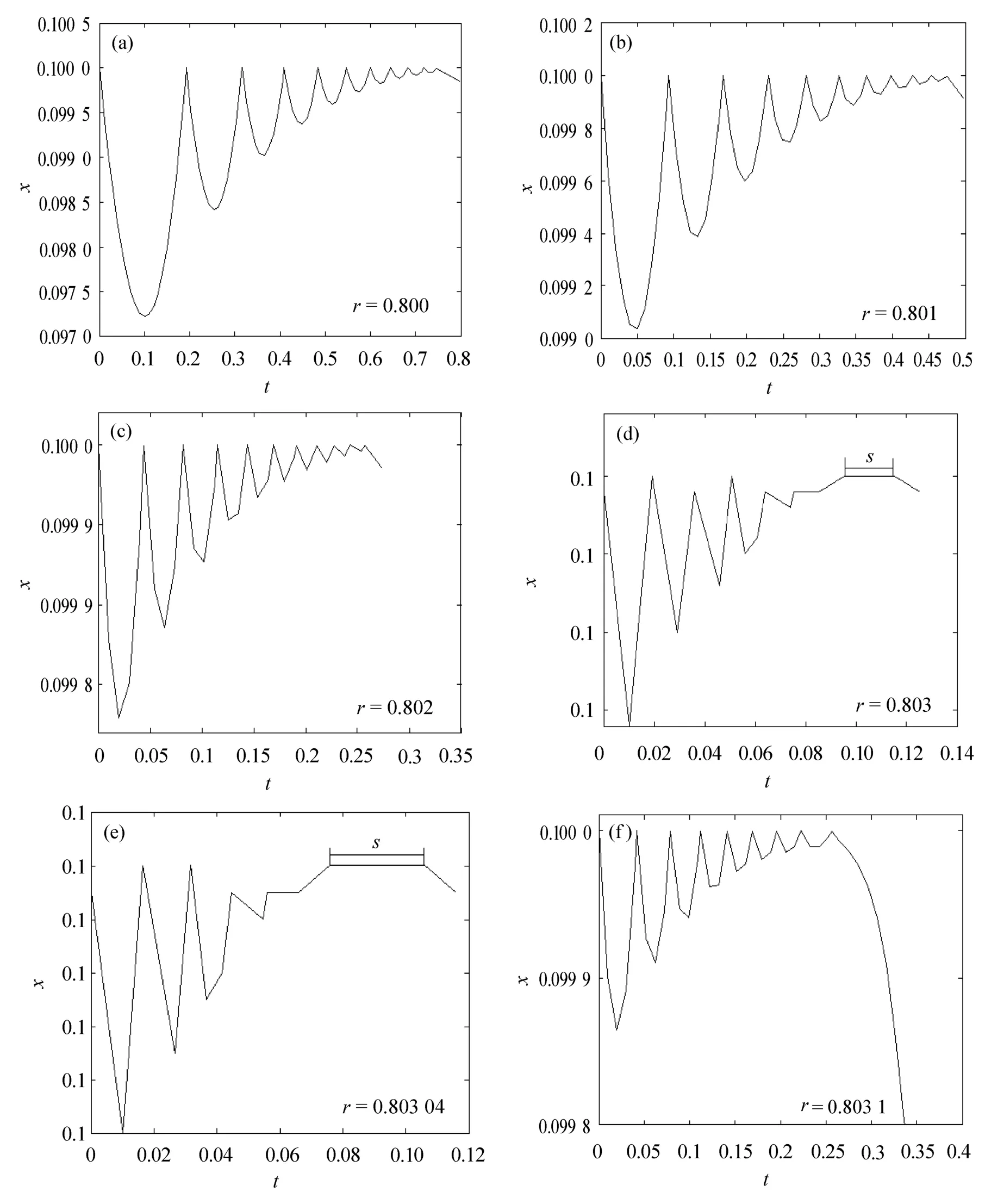
图3r取不同值时系统((4)式和(5)式)的时间历程图

4 结 语

本文引入了一种新颖的数值算法来计算碰撞振动系统的完全颤振，求得了具体的颤振完成点及颤振时间，并通过计算机数值模拟，验证了理论的正确性和可行性．本文所提出的方法适用于普通的碰撞振动系统的颤振研究，包括线性碰振系统、弱或强的非线性碰振系统．

[1] Shaw S W, Holmes P J. A periodically forced piecewise linear oscillator [J]. Journal of Sound and Vibration, 1983, 90(1): 129-155.

[2] Nordmark A B. Universal limit mapping in grazing bifurcations [J]. Physical Review E, 1997, 55(1): 266-270.

[3] Chin W, Ott E, Nusse H E, et al. Universal behaviour of impact oscillators near grazing incidence [J]. Physics Letters A, 1995, 201: 197-204.

[4] Leine R I, Nijmeijer H. Dynamics and Bifurcations of Non-Smooth Mechanical Systems [M]. Berlin: Springer, 2004: 8-33.

[5] 李群宏, 陆启韶. 一类双自由度碰振系统运动分析[J]. 力学学报, 2001, 33(6): 776-786.

[6] Fredriksson M H, Nordmark A B. Bifurcations caused by grazing incidence in many degree of freedom impact oscillators [J]. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Science, 1997, 453: 1261-1276.

[7] Nordmark A B, Piiroinen P T. Simulation and stability analysis of impacting systems with complete chattering [J]. Nonlinear Dynamics, 2009, 58: 85-106.

[8] 冯进钤, 徐伟, 牛玉俊. Duffing单边碰撞系统的颤振分岔[J]. 物理学报, 2010, 59(1): 157-162.

Chattering Analysis of a Vibrating System with Single Degree of Freedom

WANG Xiaobin1, ZHOU Peng2, HUANG Jian1
(1. School of Mathematics, Physics and Software Engineering; 2. School of Mechanic Engineering, Lanzhou Jiaotong University, Lanzhou, China 730070)

Chattering of a kind of impact oscillator system with single degree of freedom is studied. The chattering duration and the chattering complete point have been theoretically derived. Aimed at the impact problem caused by flutter in the collision system and by using the tail mapping technique, a numerical method has been found out to effectively study the chattering phenomena. Numerical simulation has also been applied to investigate the complete and incomplete chattering behaviors.

Impact; Chatter; Tail Map; Numerical Simulation

O325

A

1674-3563(2014)02-0015-07

10.3875/j.issn.1674-3563.2014.02.003 本文的PDF文件可以从xuebao.wzu.edu.cn获得

(编辑：王一芳)

2013-12-04

王小斌(1985- )，男，甘肃秦安人，硕士研究生，研究方向：非线性与动力系统