一种改进的EKPF算法在固定单站无源定位中的应用

申正义 王晴晴 王洪林 郭 锐

(空军预警学院 武汉 430019)

0 引言

有源雷达在现代战争中面临着电子干扰、反辐射攻击、低空超低空突防和隐身技术等一系列新的威胁。无源定位系统本身并不向外辐射电磁波，具有受环境影响小、隐蔽性强和作用距离远等优点。仅利用单个固定观测站接收目标辐射源辐射的信号来估计目标位置和运动状态的过程称为固定单站无源定位与跟踪。相对于多站系统，固定单站无源定位系统只需一个无源信号接收站，且不需要数据通信传输，具有更强的隐蔽性，且设备简单、系统相对独立，作为目标探测发展的重要方向和对有源雷达系统的完善和补充，将在现代电子战中发挥越来越重要的作用［1-3］。

利用角度、相位差变化率、频率和多普勒频率变化率信息实现固定单站无源定位，是一种快速高精度的定位方法。但参数测量都带有误差，为实现快速高精度的固定单站无源定位，除了要有高精度的参数测量技术外，还需要研究高性能的跟踪滤波算法，以便最大限度地利用观测量提供的目标运动信息，同时也可减轻对参数测量技术的压力。固定单站无源定位目标跟踪是典型的非线性滤波过程，经典的滤波算法是扩展卡尔曼滤波(Extended Kalman Filter，EKF)，但EKF算法存在线性化误差大，严重依赖于初始状态的选择，协方差矩阵易出现病态等问题。特别是当系统非线性较强时，这些问题会导致滤波定位结果不稳定。

针对强非线性非高斯系统，Gordon等人于1993年提出了粒子滤波(Particle Filter，PF)算法。标准PF算法选择先验概率密度作为重要密度函数，没有充分考虑当前时刻的观测值，存在粒子退化现象［4］。为此，文献［5］从改进重要密度函数的选择入手，提出了扩展卡尔曼粒子滤波算法(Extended Kalman Particle Filter，EKPF)。针对实际系统往往是非高斯非线性的情况，但文献［5］所描述的EKPF算法的本质是在重要性采样阶段用EKF算法对每个粒子进行更新，这无疑加大了算法的运算量，使算法的实时性变差。为此本文提出一种改进的EKPF算法，通过只对部分粒子进行EKF采样，在保证算法滤波性能基本不变的前提下有效降低了运算量。

1 固定单站无源定位跟踪原理

二维平面固定单站无源定位几何关系如图1所示，图中直角坐标系以阵元0中心为原点，阵元0指向阵元1的方向为X轴，T(x，y)为目标辐射源，v为目标辐射源速度矢量，vt为切向速度，vr为径向速度，ε为目标航向，r为目标辐射源相对径向距离，β为信号到达角，d为基线长度。

图1 二维平面固定单站无源定位几何关系图

1.1 目标跟踪状态方程

目标辐射源最常见的运动状态为匀速直线运动，给定其状态向量为，其中x、y表示目标位置，x·、y·表示目标运动速度。在二维平面直角坐标系下，目标跟踪随时间演化的状态方程为:

式中，υk-1为状态噪声，包含了控制项的观测误差和系统模型误差，Γ为干扰转移矩阵，Φk，k-1为状态转移矩阵:

1.2 目标跟踪观测方程

本文采用以角度、相位差变化率、多普勒频率变化率为观测量的固定单站无源定位方法［6］。根据目标状态向量与观测量之间的关系，建立系统的观测方程如下:

式中Z=(β，φ·，f·d)T为观测量，nk为观测噪声，g(·)为状态向量到观测量的非线性变换函数:

式(4)中，λ表示来波信号波长。

根据系统状态方程和观测方程，利用一定的滤波算法对目标状态进行递推估计，就可实现固定单站对空中运动目标的无源定位与跟踪。

2 改进的EKPF算法描述

2.1 EKPF算法

粒子滤波是一种基于蒙特卡罗思想的非线性、非高斯系统滤波方法，完全突破了卡尔曼滤波理论框架，它对系统的过程噪声和观测噪声没有任何限制。PF算法通过预测和更新来自于系统概率密度函数的采样集，来近似非线性系统的贝叶斯估计，从而获得状态变量的最小方差估计［7］。为了方便获取系统样本集，通常引入一个容易获取样本的重要密度函数，标准PF算法选择先验概率密度函数作为重要密度函数，由于没有考虑当前的观测值，重要性权值的方差会随时间而随机递增，使得粒子的权重集中到少数粒子上，产生粒子退化问题［8］。减轻粒子退化的有效方法是选择合适的重要密度函数。EKPF算法利用EKF算法对每个粒子进行更新，将最后得到的近似后验密度作为重要密度函数，引入了当前时刻的最新观测值，在一定程度上避免了粒子退化现象，提高了粒子滤波算法的估计精度［9］。

EKPF算法的具体运算流程如下:

a.初始化粒子

b．用EKF更新粒子

c.重要性权值计算

按式(5)计算粒子的重要性权值，并进行归一化。

d.重采样

e.状态估计

2.2 改进的EKPF算法

EKPF算法的本质是在重要性采样阶段用EKF算法对每个粒子进行更新，这无疑加大了算法的运算量，使算法的实时性变差。为此，本文对EKPF算法作如下改进:

a.在EKPF算法第2步中，用EKF算法计算粒子集的均值和方差时，只计算前N/4的粒子的均值和方差。

b.在EKPF算法第2步进行重要性采样时，从重要密度函数中采样产生前N/4的粒子，其余3N/4的粒子仍采用标准粒子算法的先验概率分布作为重要密度函数进行采样更新。

经过这样改进的算法，既考虑了当前时刻的观测值、先验概率对后验概率分布的影响，又增加了粒子的多样性，同时有效降低了计算量，提高了算法的实时性。

改进的EKPF算法的运算步骤如下:a.初始化粒子

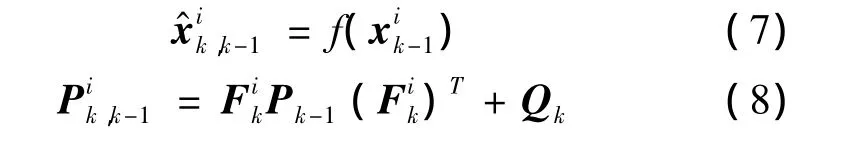
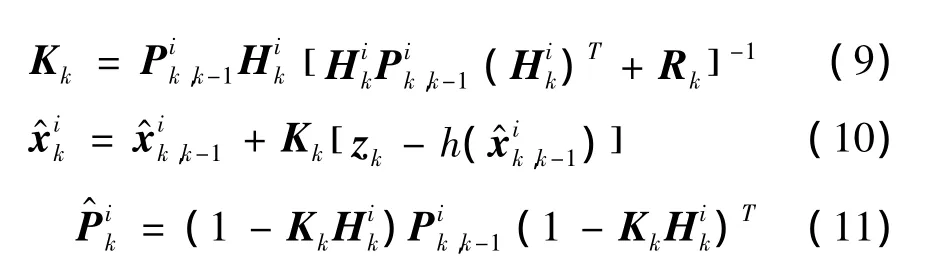
c.重要性采样

d.重要性权值计算

按式(5)计算粒子的重要性权值，并进行归一化。

e.重采样

计算Neff，若Neff＜Nth，则进行重采样，得到新的粒子集

f.状态估计

按照式(6)求出状态估计值。

3 改进算法在该定位跟踪中滤波性能仿真

3.1 仿真条件

假设在二维平面内，观测站在坐标原点处，初始位置为(90km，200km)的目标，按照V=-300m/s，50m/s的速度匀速运动，辐射源信号载频 fc=10GHz，两阵元间距d=10m。观测间隔1s，观测时间150s。为比较各算法的滤波性能，采用式(18)定义的相对径向距离误差(RPE)来描述算法的滤波性能［10］。

本文在以下两种假设下，分别进行100次蒙特卡罗实验，考察改进的EKPF算法相对于传统的EKF和EKPF算法的滤波性能。在EKPF及其改进算法中，均取粒子数 N=150，重采样门限 Nth=50。

假设一:观测量(β，˙φ，˙fd)的观测误差为(4，1，2)，观测误差单位为(mrad，mrad/s，Hz/s)，假设存在5%和20%的初始误差;

假设二:初始值为测量值［10］，观测量(β，˙φ，˙fd)的观测误差为(2，0.4，1)和(5，0.8，2)。

3.2 仿真结果分析

经Matlab软件仿真，可以得到在假设一和假设二的条件下，100次蒙特卡罗实验中三种算法的收敛次数和单次滤波所需的时间如表1所示。

表1 100次实验中各算法收敛次数及滤波耗时对比

从表中可以看出，随着初始误差的增大，EKF算法的收敛次数明显下降，而EKPF和改进的EKPF算法的收敛次数下降不明显。因此，改进的EKPF算法与传统的EKPF算法类似，都受初始误差影响较小，相对于EKF算法稳定性更好。在两种观测误差条件下，两种粒子滤波算法的收敛次数均大于EKF算法，说明粒子滤波算法在固定单站无源定位跟踪系统中的性能优于EKF算法。从单次滤波所需的时间来看，EKPF算法明显高于EKF算法，实时性较差，改进的EKPF算法相对于传统的EKPF算法滤波耗时明显下降。

为了提供三种算法更直观的滤波性能比较，图2和图3分别给出了三种算法在假设一和假设二条件下RPE的统计平均曲线。

通过对EKPF算法的理论分析和仿真实验可知，EKPF算法的运算量远大于EKF算法，这是因为EKPF算法需对每个粒子进行EKF滤波预测，其运算量约为EKF算法的N倍再加上滤波结果输出所需的运算量。而改进的EKPF算法只有N/4的粒子进行了EKF采样更新，既增加了粒子的多样性，使粒子集更能体现概率密度函数的真实分布，又有效降低了算法的运算量。仿真结果也表明，改进的EKPF算法在保证传统的EKPF算法滤波性能基本不变的前提下，有效降低了的运算量，提高了算法的实时性。

需要注意的是，从仿真结果看，相对于EKPF算法，改进的EKPF算法尽管运算量大幅下降，但其滤波耗时仍较高，这是由于计算机模拟仿真时N个粒子的运算是顺序处理的。实际工程应用中，在硬件上实现粒子滤波时N个粒子的运算是并行处理的，且随着高速计算机的出现，运算速度大幅提高，因此改进的EKPF算法仍可满足系统的实时性要求。

图2 观测误差为(4，1，2)时三种算法性能比较

图3 初始值为测量值时三种算法RPE曲线

4 结语

本文首先介绍了以角度、相位差变化率、多普勒频率变化率为观测量的定位与跟踪的基本原理，然后针对在固定单站无源定位目标跟踪中EKPF算法运算量大、实时性差的问题，对其进行了改进，提出了改进的EKPF算法。改进的EKPF算法只对N/4的粒子进行EKF采样，其余3N/4的粒子仍采用先验概率分布进行重要性采样，这样既降低了算法的运算量，又增加了粒子的多样性，使粒子集更能体现概率密度函数的真实分布。理论分析和仿真结果表明，改进的EKPF算法相对于传统的EKPF算法，在保证滤波性能基本不变的前提下，有效降低了算法的运算量，具有较好的应用价值。

［1］ 何明浩.雷达对抗信息处理［M］.北京:清华大学出版社，2010.

［2］ 熊群力，陈润生，杨小牛，等.综合电子战(第二版)［M］.北京:国防工业出版社，2008.

［3］荣思远，穆荣军，崔乃刚.EKF容错滤波方法在磁测自主导航中的应用研究［J］.电子学报，2006，34(3):2268-2271.

［4］ 朱志宇.粒子滤波算法及其应用［M］.北京:科学出版社，2010.

［5］Freitas J.F.G.，Niranjan M.，Gee A.H.Sequential Monte Carlo Methods to Train Neural Network Models［J］.NeuralComputation，2000.12(4):995-993.

［6］万方，丁建江，郁春来.利用空频域信息的固定单站无源探测定位方法［J］.探测与控制学报，2010，32(3):91-95.

［7］张建安，赵修斌，李思佳.一种用于目标跟踪的改进粒子滤波算法［J］.计算机工程，2012，38(05):176-178.

［8］胡士强，敬忠良.粒子滤波原理及其应用［M］.北京:科学出版社，2010.

［9］高静.一种改进的粒子滤波算法研究及应用［D］.延吉:延边大学，2010.

［10］郁春来.利用空频域信息的单站被动目标定位与跟踪关键技术研究［D］.长沙:国防科学技术大学，2008.