小型带不可控整流负载异步发电机自激电容确定

冯 骥，徐卫青

（国电南京自动化股份公司，江苏南京211100）

1 引言

风能、太阳能、潮汐能等一次可再生能源分布广泛，但这些能量分布往往不均匀，特别在偏远山区，传统电力很难输送到位，电力供应紧张，传统的同步发电机不仅价格昂贵，且电机自身结构复杂、维护不便、对环境的要求高，这些缺点使得同步发电机无法满足要求，在这种情况下，异步发电机的研究和应用引起了广泛的关注。异步发电机自身没有无功励磁装置，需要从电网吸收滞后无功功率，这会降低电网的电能品质，同时存在电压和频率难于调节的缺点，特别在原动机和负载变化的条件下保持异步发电机端电压和频率的稳定变得很困难，异步发电机恒压恒频输出相对是一个理想的过程，而且恒频输出也会造成原动机功率浪费，不能充分利用风能、水能等变化的能量。

随着电力电子逆变和整流技术的发展，出现了高压直流输电方式，其原理就是将发电机输出电能经过整流桥后转变为直流电，然后直流部分可以直接储存利用或者经过逆变转化为任意电压和频率要求的交流电，这样通过调节电机的转速或者无功补偿来实现电机的输出电压稳定成为唯一需要考虑的因素［1］，避免了电机频率变化带来的负面影响，提高了异步发电机输出的电能品质。

2 不可控整流桥交流侧和直流侧的电压电流关系

2.1 整流直流侧电压平均值

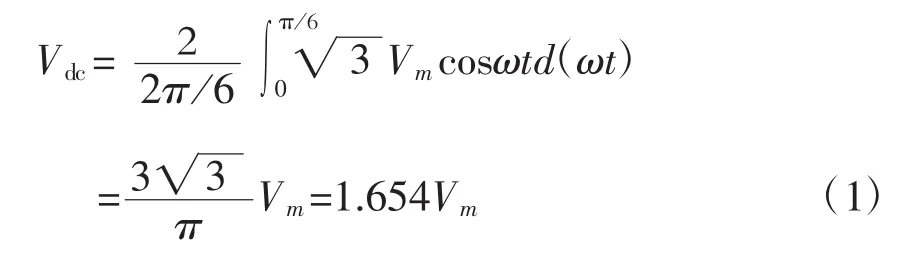
式中：Vm为交流侧相电压峰值。

2.2 输出电压的有效值

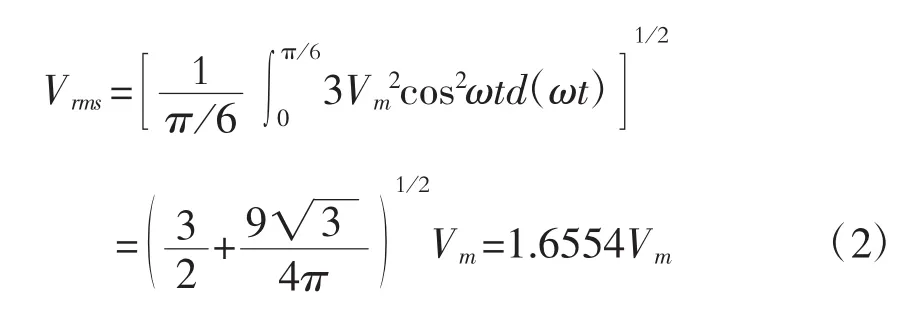
3 小型独立发电机和整流系统的电路模型

图1 异步发电机与整流桥系统

如图1所示为定子Δ形连接异步发电机和整流桥系统的简化电路图，它由以下三部分组成：①交流侧部分，由异步发电机和机端电容组成分别为定子三相电压，iD1、iD2、iD3分别为整流桥交流侧的三相电流；②整流桥部分，由6个不可控二极管组成；③直流侧部分，由负载和平波电抗器组成。

3.1 整流桥直流侧和交流侧的联系

异步发电机带整流桥后，整个线路成为非线性系统，交-直流侧以及电机通过二极管导通关断构成一个时间上不断变换的多回路系统［2］，交流侧电流不再按正弦规律变化，且含有大量谐波，但整流桥交-直侧的电压对应关系恒定不变，保持直流侧电压的稳定即保持交流侧机端电压的稳定。

设Up为图1中三相整流桥交流侧每个绕组相电压的有效值，也是定子每相激磁电容C上电压有效值，则整流桥直流侧的电压Udc可表示为：

可得

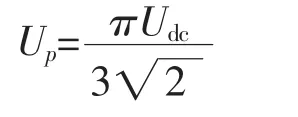
由公式（3）可知，一旦直流侧的电压给定，则交流侧的电压随之确定。由于二极管导通时有功损耗忽略不计，根据电路功率守恒原理，整流桥交-直流侧的有功功率应相等，即

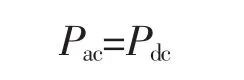
若直流侧电压Udc和负载电阻RL给定，那么直流侧消耗的有功功率为：

若把整流桥和直流侧负载部分等效为3个对称的电阻加在交流侧每相功率绕组上，则交流侧的功率为：

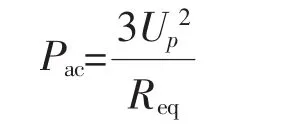
于是

这里Req代表每相绕组外加等效电阻，由公式（3）和（5）可以看出，如果直流侧电压Udc和负载RL值给定，则交流侧的每相电压Up和每相等效电阻Req也将确定，如图2所示为异步发电机和整流系统的等效模型。

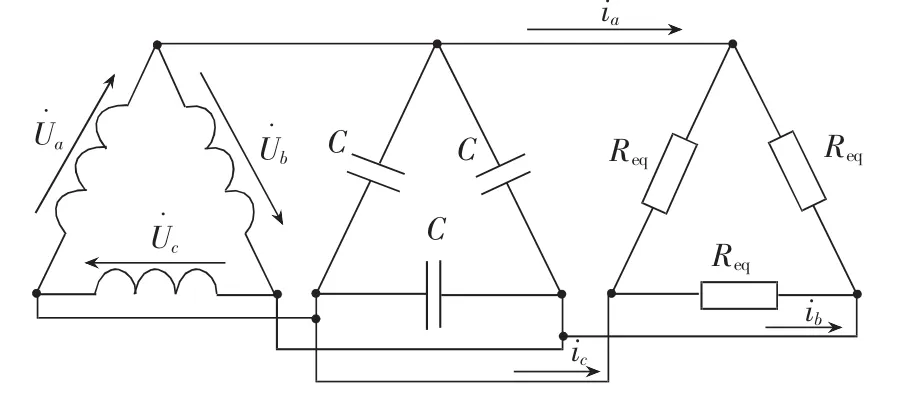
图2 异步发电机和整流系统的等效模型

这样就将非线性的整流系统模型转化为线性的等效模型，带整流负载异步发电机的分析可以转化为直接带对称电阻负载的情况［3］。

3.2 带整流系统异步发电机的等效稳态数学模型

为方便起见，在稳态分析过程中做出如下假设：①在考虑激磁电抗与感应电势的关系时对激磁电阻的作用做近似处理；②只考虑气隙磁势的空间基波分量和电势、电流的时间基波分量；③除激磁电抗受饱和程度影响外，其它电机参数均认为是常数［4］。

图3所示为异步发电机带整流负载后稳态运行时折算到基值频率fb下的一相等值电路，这里认为基值频率定子电流产生的旋转磁场转速等于恒定的转子转速，异步电机稳态运行时，定子电流产生的旋转磁场转速要小于转子转速，相应的定子频率f1要小于基值频率。

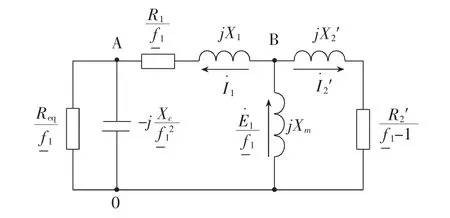
图3 异步发电机带整流系统的一相等值电路

图3中，E1为定子频率f1时的相电势；U1为定子频率f1时的端电压；R1、X1分别为基值频率fb下定子每相电阻和定子每相电抗；R2′、X2′分别为基值频率fb下转子每相电阻和转子每相电抗折算值；Xc为基值频率fb下端电容的容抗为定子侧频率标么值；转子转速的标么值为1；Xm为基值频率fb下激磁电抗。

把AO，AB和BO分别视为独立的支路，由KCL可得：

回路导纳方程

式中

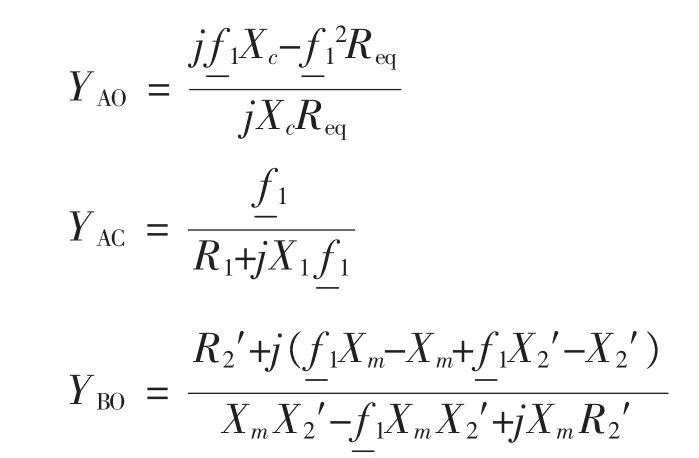
异步发电机稳态运行时机端电压不能为零，那么要使节点导纳为零，必有

即

稳态运行等值电路中的激磁电抗Xm是与感应电势相关的量，它们之间的关系可以表示为：

4 优化数学模型

优化方法求解问题的关键是选取合适的优化目标函数和约束条件，这里的约束条件是直流侧电压对应的异步发电机端电压，优化的目的是使目标函数值达到最小，从而得到所求的未知量。针对本文所分析的问题，选择节点导纳绝对值为目标函数，在给定端电压、负载、转子转速条件下，使节点导纳绝对值为零的优化收敛点所对应的即为所求值。由式（8）可知节点导纳方程中的变量有3个，机端电容容抗Xc、定子频率标么值激磁电抗Xm。在已知端电压Up，负载Req前提下可通过式（8）确定激磁电抗Xm的值，因此优化目标函数的数学模型可以表示为：

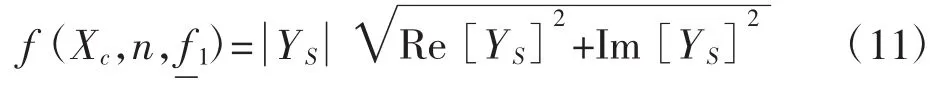
4.1 优化求解过程

对于式（8）,导纳方程取得最小值时，优化变量要满足使导纳的实部和虚部同时为零。这里采用的优化方法是由Hooke-Jeeves提出的一种多变量直接搜索法。具体的优化步骤是，首先由直流侧给定端电压和电阻大小确定交流侧端电压和等效电阻大小，然后利用公式（9）计算激磁电抗Xm，把机端电容容抗Xc、定子频率标么值作为搜索变量，并给定合理初始值和搜索步长，经过多次迭代得到的最小点即为电机的稳定运行点，也就是待求方程组的解。

4.2 Hooke-Jeeves优化算法的流程图

如图4所示为优化算法程序框图。

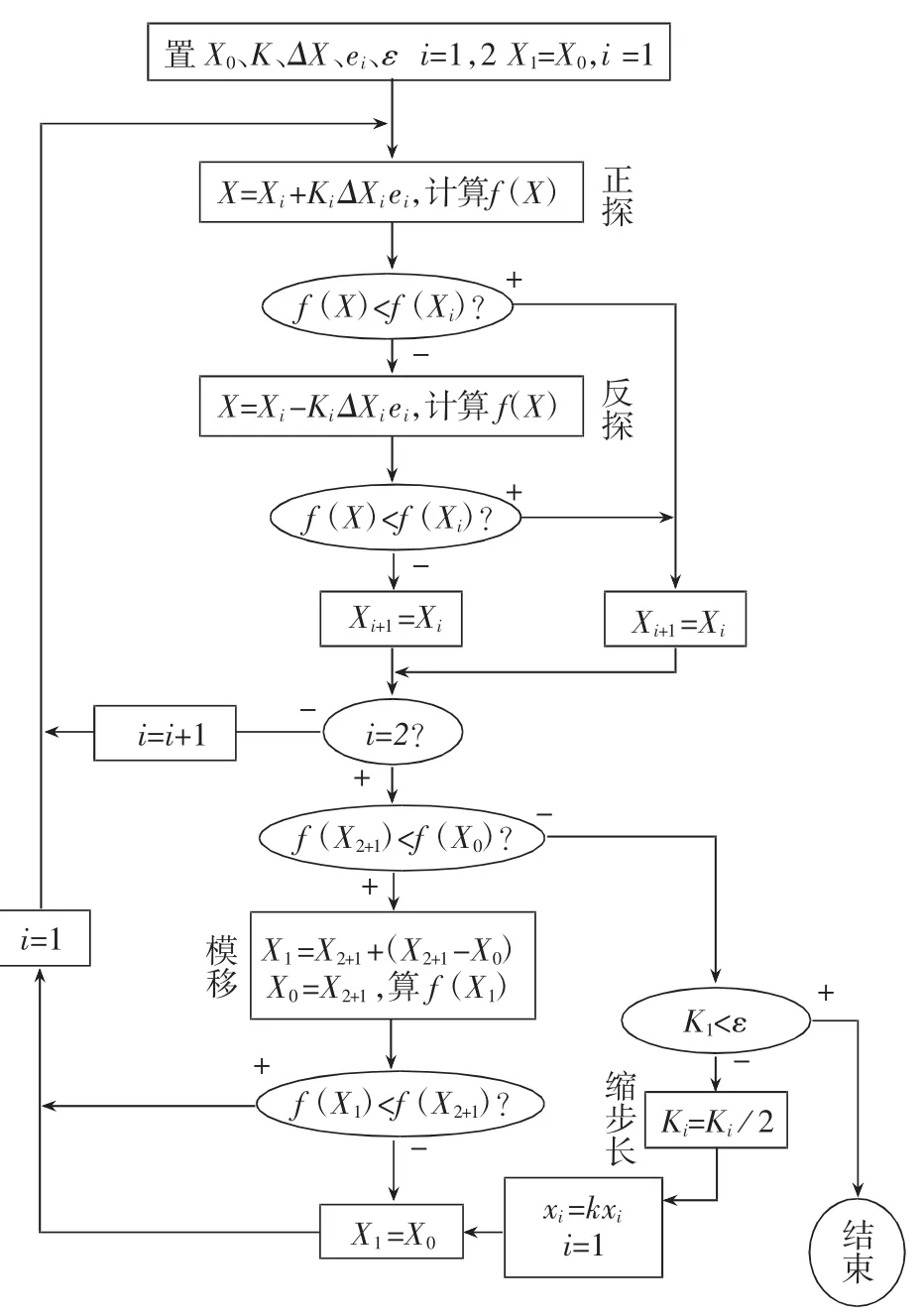
图4 优化算法程序框图

5 计算结果与实验结果分析比较

5.1 电机和整流桥参数

本文计算和实验所采用的实验室三相四极异步电机额定数据仍然和空载时电机参数一致：即额定功率2.2kW，定子Δ接，额定电压380V，额定电流5A，额定（基值）频率50Hz，额定转速为1500rpm。整流桥二极管最大峰值反向电压1500V，最大二极管平均电流40A，二极管导通压降0.7V。平波电抗器采用115mH电感，同步空载实验和堵转实验测得的一相等值电路参数为R1＝2.800Ω，X1＝3.436Ω，R2′＝3.200Ω，X2′＝3.436Ω。

E1和Xm的关系仍然表示为：

5.2 试验和仿真结果对比分析

假定直流侧欲稳定的电压为230V，分别计算了直流侧负载电阻分别为50Ω、75Ω、100Ω、150Ω、200Ω时的稳压机端电容值。然后保持电机转速1500rpm恒定，将机端电容调节到计算值，用录波仪记录直侧电压波形，得到直流侧电压平均值。计算结果和实验结果如表1所示。

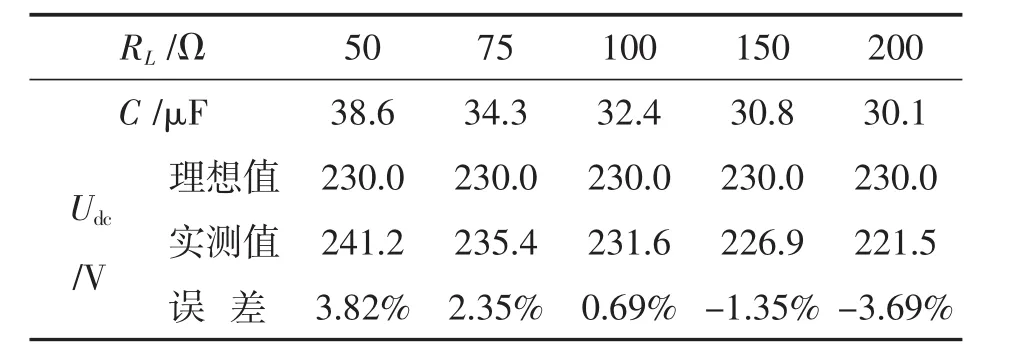
表1 不同负载下的稳压机端电容计算值和所对应的电压实验值

由表1中数据结果表明稳态后激磁电容的计算值与实测值非常接近，误差绝对值均在4%以下，说明了分析方法正确且具有较高的准确度。

6 结论

本文从异步发电机带整流桥电路出发，通过异步发电机等值电路的引入，为确定交流侧的稳压电容值提供了数学依据，通过等值电路可以求得在保持直流侧电压恒定时，任意负载情况下相应的交流侧每相激磁电容值大小。

仿真结果和实验结果均显示当整流系统直流侧负载变化时，为了保持直流侧电压恒定，利用该理论可以较准确有效地确定交流侧异步发电机相应的激磁电容值，稳定运行后直流侧电压计算值和实测值基本相等说明了分析方法的正确性和较高的准确程度。

［1］刘 芬，胡 安，刘德志.带可控整流负载的三相同步发电机的解析计算［J］.海军工程大学学报，2005，17（4）：83-87.

［2］王 晨，庄劲武.带整流负载同步发电机的Matlab仿真与试验研究［J］.电机与控制应用，2005，32（6）：10-13.

［3］刘 芬，胡 安，胡文彪.三相同步发电机带可控整流负载的性能指标计算［J］.电机与控制应用，2005，32（8）：16-19.

［4］杨 清，马伟明，吴旭升，等.同时带交流和整流负载的三相同步发电机系统的运行稳定性［J］.电工技术学报，2003，18（5）：6-10.