近道约束层析反演静校正技术在塔里木盆地复杂地区的应用
张开拓 (中石化西北油田分公司勘探开发研究院,新疆 乌鲁木齐 801000)
近道约束层析反演静校正技术在塔里木盆地复杂地区的应用
张开拓 (中石化西北油田分公司勘探开发研究院,新疆 乌鲁木齐 801000)
塔里木盆地地表起伏剧烈,近地表速度横向变化较大,静校正问题十分突出。阐述了近道约束层析反演静校正技术的基本原理,给出了该技术在塔里木盆地近地表结构复杂地区的应用结果,对比了层析反演时有、无近道约束条件下的近地表建模精度和静校正效果。应用结果表明,近道约束层析反演静校正技术在解决塔里木盆地复杂地区的静校正问题时具有明显的技术优势。
层析反演;近道约束;静校正;塔里木盆地
塔里木盆地地表起伏剧烈,近地表速度横向变化较大,静校正问题十分突出。为此,笔者采用了配套的静校正处理流程:利用近道约束层析反演技术[1~5],建立高精度近地表速度模型,计算基准面静校正量,保证准确的构造形态;在此基础上,利用初至波剩余静校正求取部分剩余高频大静校正量;最后,利用反射波剩余静校正技术求取高频小静校正量[6,7]。该静校正处理流程较好地解决了该区的静校正问题。
1 方法原理
在约束层析反演中,M条射线和N个未知数组建的层析方程组可表示为:式中:A、ΔS和ΔT分别是Jacob矩阵、慢度修正量和旅行时残差。L个约束条件建立的约束方程组可表示为:
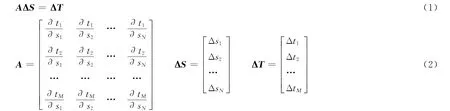

式中:C是L×N矩阵;F为一个约束条件下的旅行时残差。
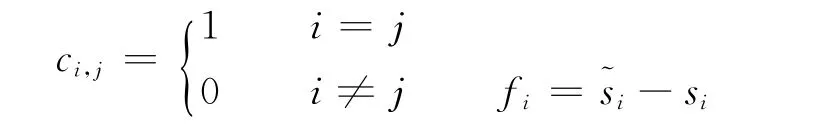
式中:si为第i个单元迭代层析反演速度值,m/s;i和j分别为速度单元和约束条件。旅行时和约束方程构建的联合方程组可表示为:

式中:B是(M+L)×N维矩阵;λ是约束权重;H是所有约束条件下的旅行时残差。拉格朗日最优约束的目标函数可表示为:
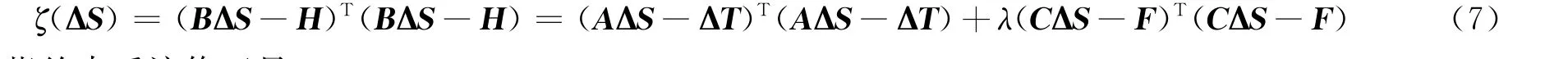
式中:ζ指约束反演修正量。
当目标函数最小时,存在∇ζ(ΔS)=0,可获得方程(5),因此方程(5)计算出的ΔS就是最优解。从目标函数(式(7))中可看出,λ=0,相当于没有约束;λ越大,目标函数中所占权重越大,约束越强。
2 实现过程
层析反演本质上讲的是一个全局寻优的过程,使理论合成时间与实际初至时间的均方差最小。由于近道射线只在浅层传播,远道射线更多地反映了深层的高速信息,所以,当输入的远道越多时,浅层模型的精度也会降低。因此,只用近道反演得到的极浅层剖面精度较高。
图1是近道约束层析反演的实现过程,全炮检距初至时间通过近道反演得到的近道反演模型和权重场作为约束条件进行迭代反演,得到最终的速度模型。
3 应用效果分析
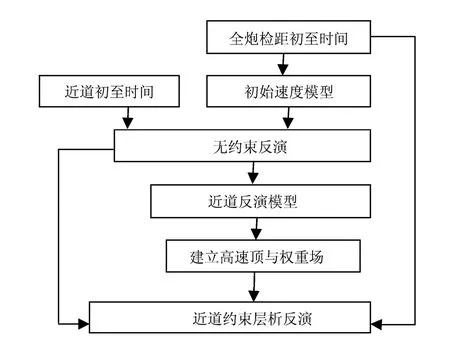
图1 近道约束层析反演的实现过程
理论上讲,如果知道了真实的近地表速度模型,静校正问题就能彻底解决。所以,解决复杂探区静校正问题的核心就是建立高精度的符合实际地质情况的近地表速度模型。因此,用近道反演得到精度较高的极浅层来约束整个速度反演过程,可以得到更准确的近地表速度模型。
塔里木盆地某二维工区跨越多个构造区域,地表结构非常复杂,速度横向变化大,所以采用了近道约束来控制反演速度,以保证反演速度模型的正确性和静校正结果的有效性。图2是有、无近道约束的近地表速度模型对比图,可以看出,利用近道约束反演计算出的近地表速度模型精度比无近道约束的近地表速度精度要高。
图3是有、无近道约束层析反演的单炮对比,可以看出,采用约束反演的单炮初至曲线初至光滑,性噪比有所提高。
图4是近道约束反演静校正与野外静校正叠加剖面对比,可以看出,近道约束反演静校正能够有效地解决长波长问题,叠加剖面信噪比明显提高。

图2 有(a)、无(b)近道约束的近地表速度模型对比图

图3 有(a)、无(b)近道约束层析反演的单炮对比

图4 近道约束反演静校正与野外静校正叠加剖面对比图
4 结语
约束层析反演静校正方法在塔里木盆地复杂地区的应用情况表明,该方法利用近道信息约束,比一般常规层析反演静校正能够更准确地反演出表层低速带的速度模型,比野外静校正更适用于复杂地区。该方法在西部复杂地表区有良好的应用前景。
[1]熊翥.复杂地区地震数据处理思路[M].北京:石油工业出版社,2002.
[2]何樵登.地震勘探原理和方法[M].北京:地质出版社,1986.
[3]陆基孟.地震勘探原理[M].北京:石油工业出版社,1991.
[4]渥·伊尔马兹.地震资料分析[M].刘怀山,等译.北京:石油工业出版社,2006.
[5]赵妍.层析成像静校正方法研究[D].东营:中国石油大学(华东),2009.
[6]杨举勇,杨金华,彭更新,等.塔里木盆地沙漠地震勘探技术及应用[M].北京:石油工业出版社,2009.
[7]钟本善,周熙襄.中国西部地区地震勘探的静校正问题[J].物探化探技术,1999,21(4):358~366.
[编辑]龚丹
P631.44
A
1000-9752(2014)02-0070-03
2013-04-08
张开拓(1987-),男,2008年长江大学毕业,助理工程师,现主要从事石油地震资料处理工作。

