严重拖尾杂波中距离扩展目标的自适应极化检测

赵宜楠，庞晓宇，王 军，周志权

严重拖尾杂波中距离扩展目标的自适应极化检测

赵宜楠，庞晓宇，王 军，周志权

（哈尔滨工业大学（威海）信息与电气工程学院，264209山东威海）

为了解决统计特性未知的严重拖尾杂波背景下距离扩展目标的信号检测问题，提出了一种基于广义似然比检验（GLRT）的自适应极化检测器.该检测器利用了雷达回波的极化信息，并使用辅助数据估计杂波的协方差矩阵.推导了其虚警概率表达式，理论分析验证了该检测器对于杂波能量和杂波协方差矩阵具有恒虚警特性.仿真结果表明，该自适应极化检测器在较低信杂比下就可以获得好的检测性能，且相比于点目标自适应极化检测器和单极化自适应检测器，具有更优的检测性能.

自适应检测；距离扩展目标；极化；复合高斯；逆伽马

距离扩展目标（range distributed target，RDT），指的是尺寸远大于雷达距离单元的目标；其等效散射体会分布在多个连续的距离单元内.随着高分辨率雷达的广泛应用，RDT的检测问题已成为雷达技术研究领域中的重要研究内容.高分辨率雷达可以提高目标的检测能力，其主要原因为:1）雷达的高距离分辨力降低了单个距离单元中杂波反向散射的能量［1］；2）RDT比未进行距离分解的点目标波动小［2］.杂波中距离扩展目标的检测问题通常使用高斯、非高斯和复合高斯（compound Gaussian，CG）杂波模型［3-7］.

极化分集作为增强雷达系统检测能力的有效手段之一，已被广泛的研究和应用.文献［8-9］针对高斯杂波背景，研究点目标的极化检测问题.然而，实测数据表明，在低掠角或采用高分辨率雷达条件下，CG模型与真实杂波信号分布情况更加匹配［10，11］.Lombardo等人［12］提出了CG杂波背景下点目标的极化检测器，并验证了其恒虚警（CFAR）特性，然而该检测器只针对于点目标，而没有考虑对RDT的检测.

本文针对严重拖尾CG杂波，提出一种基于广义似然比检验（GLRT）的RDT自适应极化检测器，并对其检测性能和虚警概率进行了分析.

1 杂波模型

在CG模型下，杂波建模为散斑分量与纹理分量乘积的形式，其中纹理分量为慢变的非负随机过程，而散斑分量为快变的复高斯过程，且二者相互独立［10］，纹理分量调制散斑分量.则海杂波复包络可以为

式中:g为协方差矩阵为C的散斑分量，τ为纹理分量．

复合高斯模型的关键问题在于纹理分量分布的选择，对于纹理分量的概率密度函数（PDF）严重拖尾的情况通常使用伽马分布和逆伽马分布（inverse Gamma，iΓ），实测数据表明使用iΓ分布更合适［13］.

纹理分量的iΓ分布PDF表示为

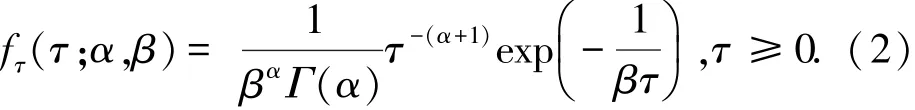
2 检测器设计

2.1 检测问题描述

假设雷达发射N个相干脉冲串，经过解调、匹配滤波、采样得到雷达回波．定义x（n）=［xh（n），xv（n）］T为雷达的极化发射信号，xh（n），xv（n）分别为发射信号的水平、垂直极化分量；y（n）=［yh（n），yv（n）］T为雷达的复包络接收信号，yh（n），yv（n）分别为接收信号的水平、垂直极化分量；r（n）=［rh（n），rv（n）］T为复合高斯杂波，rh（n），rv（n）分别为杂波的水平、垂直极化分量；在考虑杂波的应用场景中，杂噪比通常较大，为了简化，此处忽略测量噪声，接收信号可以表示为

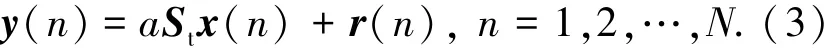
如果将信号用矢量描述，那么Y=［y（1），…，y（n）］，X=［x（1），…，x（n）］，R=［r（1），…，r（n）］，其中Y，X，R均为2×N维矩阵．那么式（3）可以表示为

其中:a为目标的幅度，St为目标极化散射矩阵

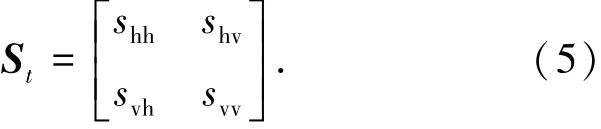
St各元素下标的两个字母分别代表发射和接收通道．对于单站的情况，St=STt．

RDT的检测问题就可以描述为二元假设检验问题为

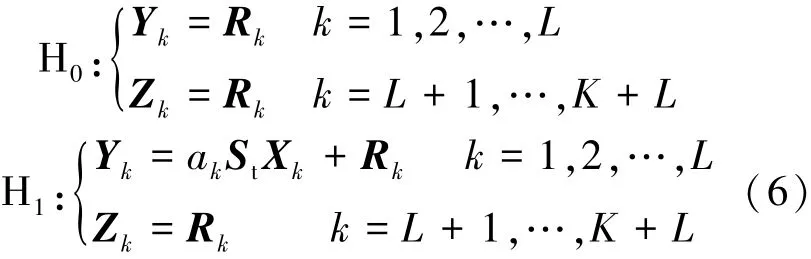
其中:把可能存在目标的检测单元数据Y1，Y2，…，YL称为主数据，将不含目标、与主数据有相同杂波协方差矩阵结构的检测单元数据ZL+1，ZL+2，…，ZL+K称为辅助数据．

Rk建模为纹理分量为iΓ分布的CG模型，即Rk=τk为纹理分量，g为协方差矩阵为C的散斑分量，则C=E（ggH）．对于给定的纹理分量，杂波的条件数学期望为则H0假设下Yk的条件PDF可以表示为

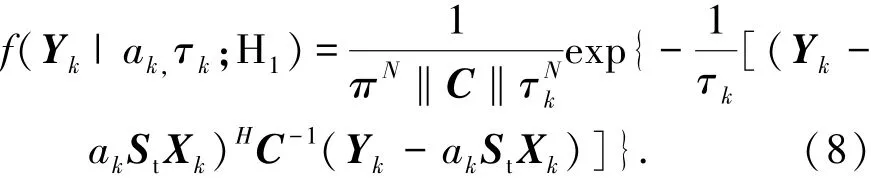
两个假设下Yk的PDF可以通过以下积分处理得到.

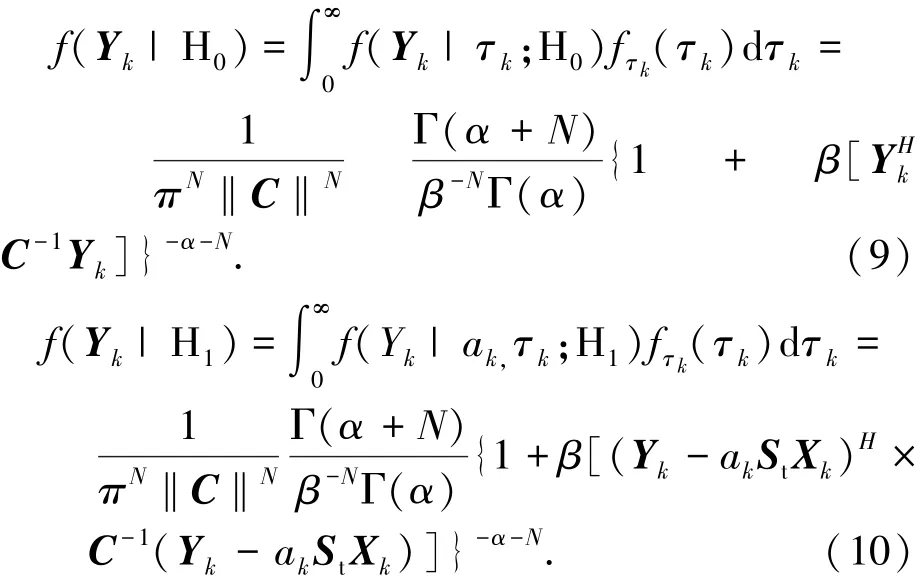
同样的H1假设下Yk的条件PDF可以表示为

式中:‖·‖表示矩阵的行列式，iΓ分布的PDF由形状参数α和尺度参数β决定，假设这些参数先验已知或可以估计得到．

2.2 自适应极化检测算法

由于缺少目标幅度和杂波分布的完整知识，这里采用GLRT，即在似然比检验中使用未知参数的最大似然估计值代替未知参数来解决问题［14］.自适应极化检测器的推导步骤如下所示:

第1步，假设纹理分量τk已知，通过目标幅度ak使似然比最大化，进而得到主数据的广义似然比，即

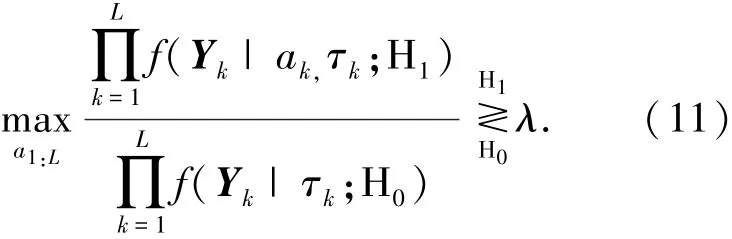
将式（7）、（8）代入上式，检测器可以化简为

上式中的目标幅度＾ak是H1假设为真时未知参数ak的最大似然估计值.

第2步，对式（10）求导，即

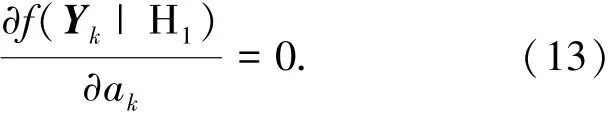
进一步化简可得目标幅度的最大似然估计值＾ak，即

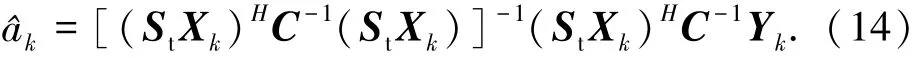
第3步，计算得到τk的最大后验（MAP）估计值［14］，即

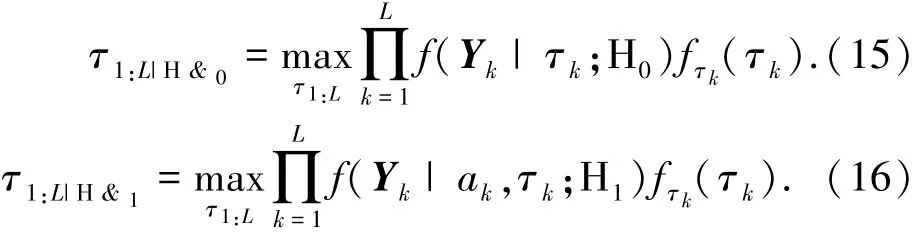
将式（2）、（7）、（8）代入上式，通过求导可得

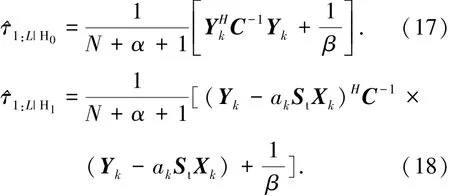
将＾ak，＾τ1:L｜H0，＾τ1:L｜H1代入到式（12）中并进行化简，可得

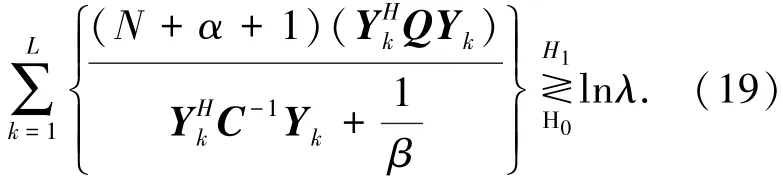
其中:Q=C-1p（pHC-1p）-1pHC-1，p=Stx，对上式两侧同时取对数并进行化简，得到检测器最终表达式为

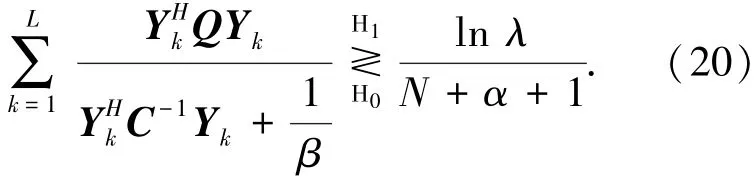
第4步，实际上，CG杂波中散斑分量的协方差矩阵是未知的，需要利用辅助数据进行估计.为消除局部的杂波能量影响，上式中的协方差矩阵采用归一化的样本协方差矩阵估计值代替［14］

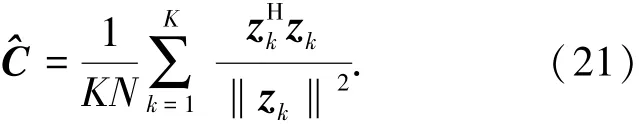
其中:zk为辅助数据．将式（21）代入式（20），就可以得到自适应极化检测器．当L=1时，目标只存在于一个距离单元内，则所提出的检测器与点目标的检测器相匹配.为了方便描述，这里将本文提出的算法称为ARDTPD（adaptive range distributed target polarimetric detector），将自适应点目标极化检测器称为APD（adaptive polarimetric detector）.

2.3 虚警概率分析

因为使用了CG模型，可以得到检测器虚警概率的闭合表达式.当L=1时［15］式（20）化简为

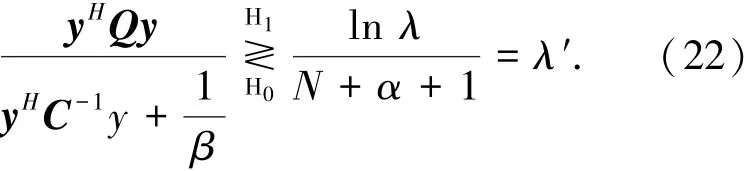
对式（22）白化，定义

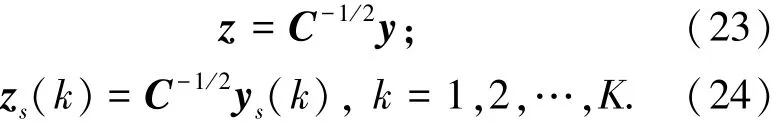
其中:z，zs（k）为2×1的复高斯向量，其均值为零，协方差矩阵为单位阵.那么可以得到

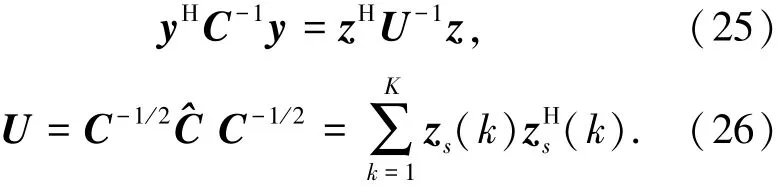
定义T=C-1／2p（pHC-1p）-1／2，将T，U代入式（22）得到

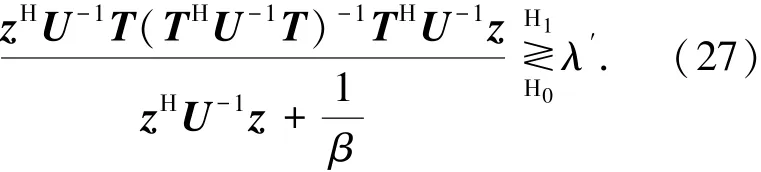
上述公式可以表示为

其中:2t和2τ服从中心χ2分布，其自由度分别为4和2＆（K-2N+1）［16］．上式可以变换为

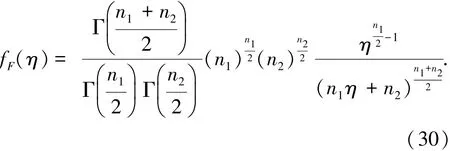
其中:Γ（·）为伽马函数，n1=2（K-2N+1），n2=4．

当L=1时，检测统计量为Δ=1／（1+η），其PDF为

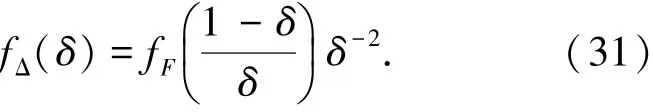
虚警概率为

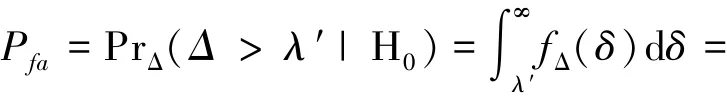
当L＞1时，检测统计量为

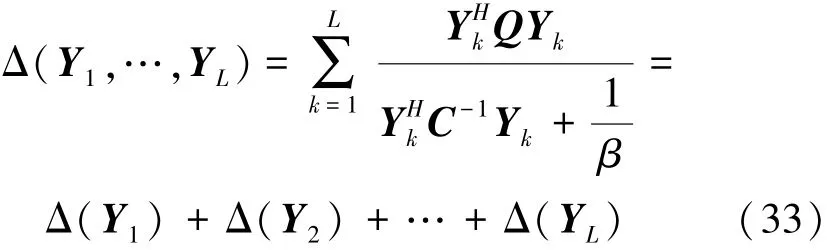
当i≠j i，j∈｛1，2，…，L｝时，Δ（Yi）与Δ（Yj）独立，因此在H0假设下可得

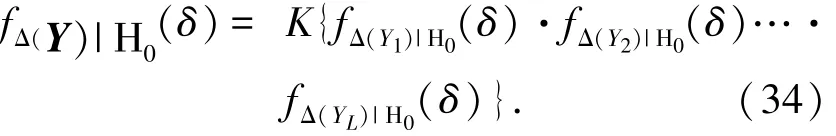
其中:K为PDF的归一化常数.则在H0

假设下，L＞1时的虚警概率公式为

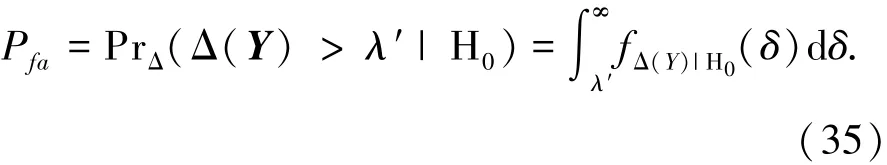
可以看出式（30）、（32）、（35）中均不包含杂波分布的相关参数，理论验证了ARDTPD的CFAR性能.

3 性能分析及仿真结果

3.1 检测性能

采用蒙特卡洛仿真方法得到自适应极化检测器的检测性能曲线，并对其检测性能进行分析，仿真参数设置如下:

定义信号杂波功率比（RTC）为

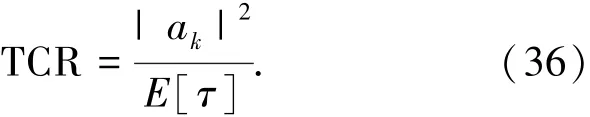
式中:ak为目标的幅度；E［τ］为纹理分量的均值．

散斑分量的协方差矩阵的第（p，q）个元素定义为

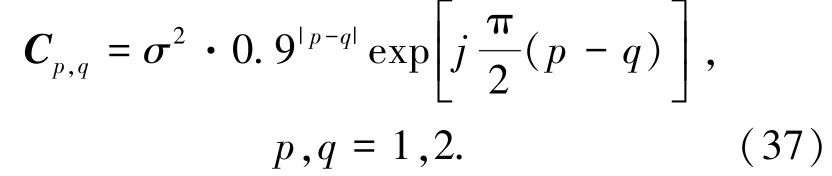
其中:σ=2.05．假定雷达发射波的水平和垂直极化交替出现，观测样本数为N=8，目标存在L= 3个距离单元内，可以得到K=20个距离单元的辅助数据．蒙特卡洛仿真次数由100／PFA决定．

图1比较了信杂比分别取-2、-5、-8 dB情况下，ARDTPD的ROC曲线.其中iΓ分布纹理分量的形状参数假设为ν=1.5，虚警概率从10-6变化到100，由图可知:ARDTPD即使在较低信杂比下也可以获得好的检测性能.

图2比较了ARDTPD与假设散斑分量协方差矩阵先验已知时的极化检测器的检测性能.定义虚警概率PFA=10-3，iΓ分布纹理分量的形状参数假设为ν=1、1.5、2的3种情况.由图2，可以得到以下结论:1）当形状参数降低时，两个检测器的检测性能均降低；2）在信杂比较低时（＜0 dB），也可以获得满意的检测概率；3）它们具有相近的检测性能，形状参数越大，性能越接近.

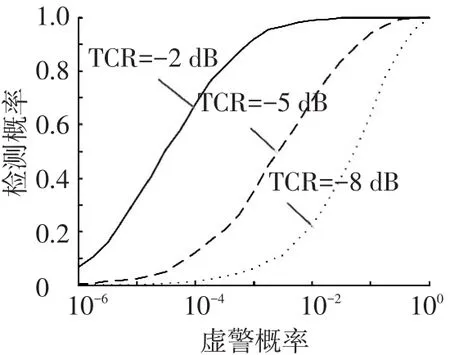
图1 不同信杂比下ARDTPD的ROC曲线

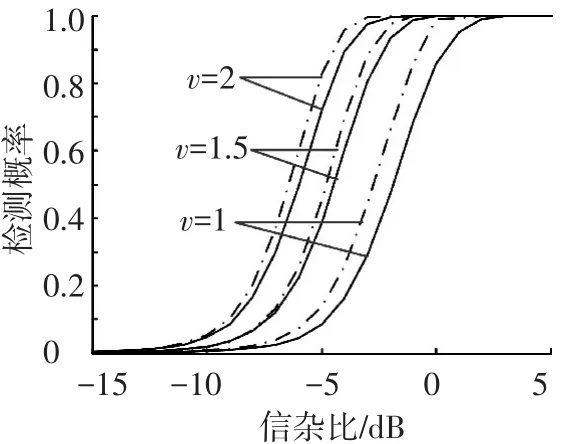
图2 ARDTPD（实线）和协方差矩阵完全已知时的检测器（虚线）的检测性能曲线

图3比较了ARDTPD与APD的检测性能，仿真参数同上，由图中可明显看出，相比APD，ARDTPD对于本文考虑的雷达场景和信号模型具有明显的优势.

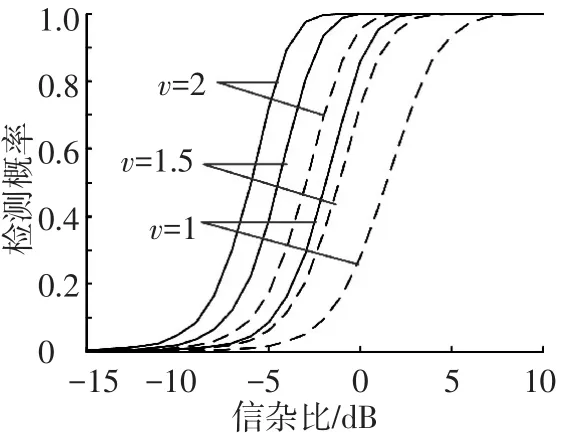
图3 ARDTPD（实线）和APD（虚线）的检测性能曲线

图4比较了ARDTPD和单极化自适应检测器的检测性能，表明ARDTPD的检测性能优于单极化自适应检测器的检测性能.

3.2 虚警概率分析

｀2.3小节通过理论推导验证了ARDTPD的CFAR特性，本节对虚警概率随杂波能量起伏的稳定性进行仿真分析.假设取值不同的纹理分量均值E［τ］代表杂波能量的起伏，形状参数ν分别取1、1.5、2，其他仿真参数设置同上.通过蒙特卡洛仿真，分析H0假设下的检测器虚警概率特性，仿真结果如图5所示.由图5的仿真结果可知，ARDTPD相对于杂波能量具有CFAR特性，与2.3节的分析一致.

图4 ARDTPD（实线）和单极化自适应检测器（虚线）的检测性能曲线

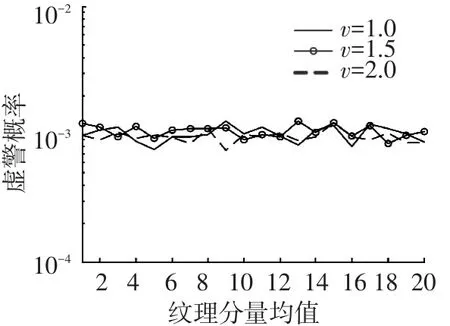
图5 纹理分量均值与虚警概率的关系

4 结 论

1）提出了一种针对RDT的自适应极化检测器ARDTPD.该检测器适用于以iΓ分布为纹理分量的CG杂波环境.其利用辅助数据对杂波协方差矩阵进行了估计，使检测器具有杂波稳健性.

2）分别通过理论推导和仿真分析，验证了其相对于杂波能量和杂波协方差矩阵具有恒虚警特性.

3）通过蒙特卡洛仿真，比较了ARDTPD与散斑分量协方差矩阵先验已知的极化检测器、点目标自适应极化检测器和单极化自适应检测器的检测性能，验证距离了扩展目标自适应极化检测器的优越性.

［1］秦建.极化宽带雷达的自适应目标检测［D］.哈尔滨:哈尔滨工业大学，2011.

［2］CONTE E，DE MAIO A，RICCI G.GLRT-based adaptive detection algorithms for range-spread targets［J］.IEEE Trans on Signal Processing，2001，49（7）: 1336-1348.

［3］SHUAI Xiaofei，KONG Lingjiang，YANG Jianyu. Performance analysis of GLRT-based adaptive detector for distributed targets in compound-Gaussian clutter［J］. Signal Processing，2010，90（1）:16-23.

［4］CONTE E，DE MAIO A.Distributed target detection in compound-Gaussian noise with Rao and Wald tests［J］. IEEETransactionsonAerospaceandElectronic Systems，2003，39（2）:568-582.

［5］HE You，JIAN Tao，SU Feng，et al.Novel range-spread target detectors in non-Gaussian clutter［J］.IEEE Transactions on Aerospace and Electronic Systems，2010，46（3）:1312-1328.

［6］LIU Bin，CHEN Biao，MICHELS J H.A GLRT for multichannel radar detection in the presence of both compound Gaussian clutter and additive white Gaussian noise［J］.Digital Signal Processing，2005，15（5）: 437-454.

［7］ALFANO G，DE MAIO A，CONTE E.Polarization diversity detection of distributed targets in compound-Gaussian clutter［J］.IEEE Transactions on Aerospace and Electronic Systems，2004，40（2）:755-765.

［8］DE MAIO A，RICCI G.A polarimetric adaptive matched filter［J］.Signal Processing，2001，81（12）:1194-1206.

［9］PASTINA D，LOMBARDO P，BUCCIARELLI T. Adaptive polarimetric target detection with coherent radar I:detection against Gaussian background［J］. IEEETransactionsonAerospaceandElectronic Systems，2001，37（4）:1194-1206.

［10］CONTE E，DE MAIO A，GALDI C.Statistical analysis of real clutter at different range resolutions［J］.IEEE Transactions on Aerospace and Electronic Systems，2004，40（3）:903-918.

［11］FARINA A，GINI F，GRECO M V，et al.High resolution sea clutter data:A statistical analysis of recorded live data［J］.IEE Proceedings，Radar，Sonar Navigation，1997，144（3）:121-130.

［12］LOMBARDO P，PASTINA D，BUCCIARELLI T. Adaptive polarimetric target detection with coherent radar II:detection against non-Gaussian background［J］.IEEE Transactions on Aerospace and Electronic Systems，2001，37（4）:1207-1220.

［13］BALLERI A，NEHORAI A，WANG Jian.Maximum likelihood estimation for compound-Gaussian clutter with inverse gamma texture［J］.IEEE Transactions on Aerospace and Electronic Systems，2007，43（2）:775-779.

［14］SHANG Xiuqin，SONG Hongjun，WANG Yu，et al. Adaptive detection of distributed targets in compound-Gaussian clutter with inverse gamma texture［J］.Digital Signal Processing，2012，22（6）:1024-1030.

［15］王伟国，赵宜楠，乔晓林.复合高斯杂波中距离分布目标的极化自适应检测［J］.宇航学报，2012，8（33）:1138-1140.

［16］PARK H R，LI Jian，WANG Hong.Polarization-spacetime domain generalized likelihood ratio detection of radar targets［J］.Signal Processing，1995，41（2）: 153-164.

（编辑 魏希柱）

Adaptive polarimetric detection of range spread targets in heavy-tailed compound-Gaussian clutter

ZHAO Yinan，PANG Xiaoyu，WANG Jun，ZHOU Zhiquan
（School of Information and Electrical Engineering，Harbin Institute of Technology at Weihai，264209 WeiHai，Shandong，China）

The problem of detection for range spread targets is analyzed in complex clutter with unknown statistical characteristics.With polarization information of radar echo and training data available to estimate covariance matrix of clutter，a generalized likelihood ratio test（GLRT）based adaptive polarimetric detector is proposed.Then，the analytic expression of false alarm probability is derived to prove constant with respect to the clutter energy and clutter covariance matrix in theory.The simulation results show that the adaptive polarmetric detector achieves good detect probability even at a low target to clutter ratio，and has better detection performance than the adaptive polarimetric detector of point target and the adaptive detector using single polarization.

adaptive detection；range spread targets；polarization；compound-Gaussian；inverse Gamma

TN953.5

A

0367-6234（2014）04-0070-05

2013-03-11.

国家自然科学基金资助项目（61371181）；山东省自然科学基金资助项目（ZR2012FQ007）.

赵宜楠（1977—），男，副教授，博士生导师；

周志权（1973—），男，教授，博士生导师.

赵宜楠，hrbzyn＠163.com.