双材料界面裂纹奇异性及应力强度因子

刘晓红，李俊林，谢秀峰，李沐阳(太原科技大学 应用科学学院，太原 030024)

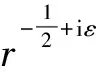
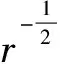
1 新应力函数

如图1所示，y>0部分为第一种正交异性材料，其材料工程常数为E11,E12,v11,v12,μ1；y<0部分为第二种正交异性材料，其材料工程常数为E21,E22,v21,v22,μ2；x≤0，y=0为界面裂纹；x>0，y=0为材料粘接界面；r和θ为从裂纹边缘起度量的极坐标。

应力函数Uj(j=1,2)满足控制方程：

(1)

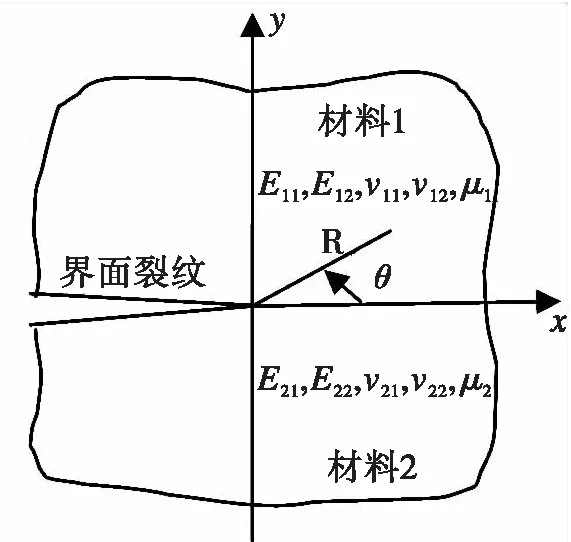
图1 正交异性双材料半无限界面裂纹模型

系数(b11)j,(b12)j,(b22)j,(b66)j分别为：

连续边界条件为：

θ=±π:(σθ)1=(σθ)2=0,(τrθ)1=(τrθ)2=0

(2)

θ=0:(σθ)1=(σθ)2,(τrθ)1=(τrθ)2

(3)

θ=0:(ur)1=(ur)2,(uθ)1=(uθ)2

(4)

令ηjk满足控制方程组(1)的特征方程组：

(5)

此方程组的判别式有三种情形，分别为：△1>0,△2>0；△1<0,△2<0；△1>0,△2<0.本文仅讨论判别式△1>0,△2>0情况(其他两种情形可类似讨论)。

此时方程组(5)的根为：

由控制方程(1)及界面裂纹边界条件(2)-(4)，构造含有复奇异指数的新应力函数为：

(6)

其中λ为未知的复奇异指数，Ajk、Bjk为待定的复参数。

(7)

2 四种奇异性

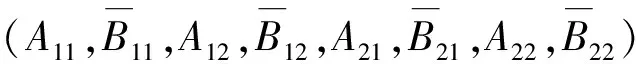
对方程组的系数行列式进行适当的初等变换后，它们系数矩阵的行列式均为：

(8)

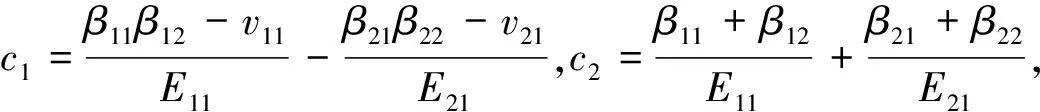
(9)

为使线性方程组有一组非零解，则系数行列式必须为0.

若sinλπ=0时，则λ=n(n=0,1,2…).因与复合材料工程常数无关，舍去此λ.

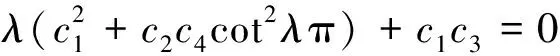
(10)

由式(10)可知c2>0，c4>0，以下通过c1c3中上下材料的不同讨论复奇异指数λ的取值。

1)当c1c3=0时，分情况讨论复奇异指数λ的值。

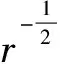
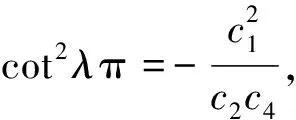
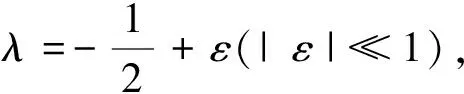
(11)

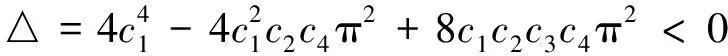
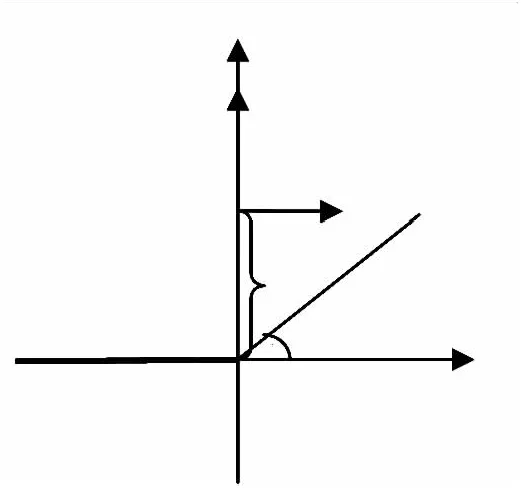
图2 半无限裂纹加载荷

3 应力强度因子

如图2所示，半无限界面裂纹在x=0，y=h处受集中复载荷R=Q+iP作用，其边界条件为：

(12)

由弹性力学知：

(13)

Re(Ajk+Bjk)=ajkRe(A22+B22),Im(Ajk+Bjk)=bjkIm(A22+B22)

(14)

由式(6)，式(12)-(14)可求得自由量Re(A22+B22)，Im(A22+B22)的表达式。

结合式(13)，可得应力强度因子的计算式为：

(j=1,2)

(15)

Re(Ajk+Bjk)=-ajkIm(A22+B22),Im(Ajk+Bjk)=bjkIm(A22+B22),(j=1,2；k=1,2)

(16)

由式(6)，式(12)-(13)，结合式(16)可得自由未知量Im(A22+B22)的表达式。

结合式(13)，可得应力强度因子的计算式为：

(17)

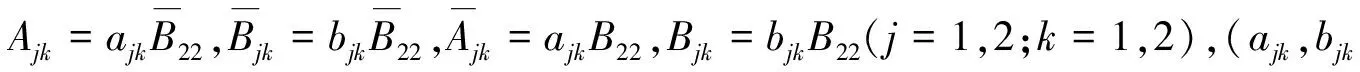
(18)

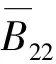
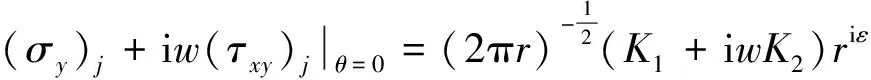
(19)

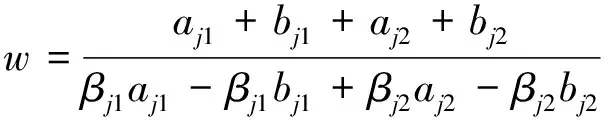
由式(6)、式(13)，结合式(19)，可得应力强度因子的计算式为：

(20)

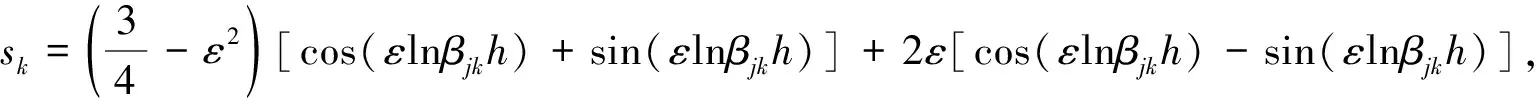
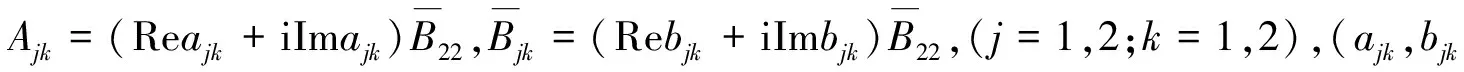
(21)

结合式(13)，定义应力强度因子[3]为：

(22)

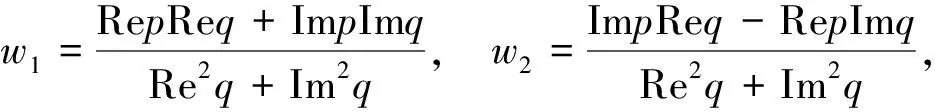
p=aj1+bj1+aj2+bj2,q=βj1aj1-βj1bj1+βj2aj2-βj2bj2

由式(6)、式(13)，结合式(22)，可得应力强度因子的计算式为：

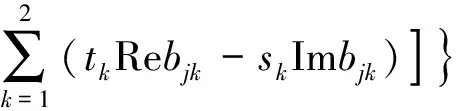
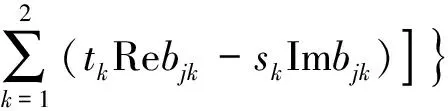
(23)

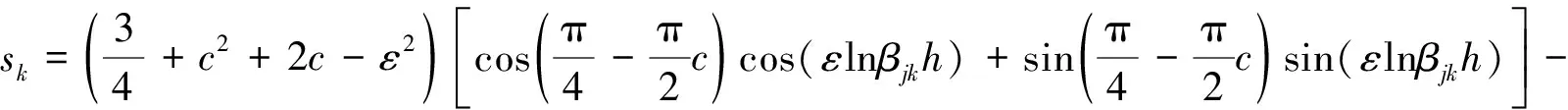
4 四种奇异性算例分析

由以上推导，选取适当的正交异性复合材料弹性工程常数[10]，进行算例分析如下，结果验证了正交异性双材料半无限界面裂纹四种应力奇异性的存在。

表1 材料工程参数

表2 四种奇异指数

注：表中数据精确到千分位。

5 结论

本文在含有实奇异指数的应力函数的基础上，构造了含有复奇异指数的新应力函数，采用复合材料断裂复变方法，对正交异性双材料界面裂纹应力奇异性问题进行了研究。系统地讨论了双材料工程参数与应力奇异性之间的关系。主要结果如下：

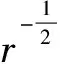
(2)在给定载荷条件时，得出了四种奇异性下应力强度因子的计算公式。

参考文献：

[1] WILLIAMS M L.The stresses around a fault or crack in dissimilar media[J].Bulletin of the Seismological Society of America，1959，49(2)：199-204.

[2] SIH G C，RICE J R.The bending of plates of dissimilar materials with cracks[J].Journal Of Applied Mechanics，1964，31：477- 482.

[3] 许金泉.界面力学[M].北京：科学出版社，2006.

[4] SUO Z G，Singularities，interfaces and cracks in dissimilar anisotropic media [J].Mathematical and Physical Sciences，1990，427 (A)：331-358.

[5] Li Junlin，Zhang Shaoqin，Yang Weiyang.Stress field near interface crack tip of double dissimilar orthotropic composite materials[J].Applied Mathematics and Mechanics，2008(8)：1045-1052.

[6] 李俊林，张少琴，杨维阳等.正交异性双材料半无限界面裂纹尖端场分析[J].应用力学学报，2010，27(3)：444-450.

[7] Yang XiaoMei，Yang Weiyang，Li Junlin，Zhang Xuexia.Fracture analysis near the interface crack tip for mode I of orthotropic bimaterial[J].Science China，2013(4)：785-797.

[8] 徐芝纶.弹性力学第4版[M].北京：高等教育出版社，2006.

[9] 杨维阳，张少琴.关于复合材料单层板I型裂纹尖端附近应变场和位移场的探讨[J].太原重型机械学院学报，1987，8(1)：77-87.

[10] 沃丁柱.复合材料大全[M].北京：化学工业出版社，2000.