多轴车辆轴荷的分配与影响因素研究

王 镇，贾志绚，张喜清(太原科技大学机械工程学院，太原 030024)

车轴轴荷是多轴车辆方案设计过程中进行总体布局、车架强度校核、整车动力学分析尤其是车辆制动性能分析评估时的必要参数[1]。许多作者对多轴轴荷的计算问题进行过深入研究：徐继等引入外心距的概念，对多轴轴荷的计算方法进行了讨论，当外心距相对轴距过大时，容易带来较大的计算误差[1]；张凤鸣基于能量原理，讨论了长轴距多轴轴荷的计算方法，在实际应用中需要对基本体系作弯矩图，利用图乘法计算积分[2]。

在以往的研究基础之上，以某九轴全地面起重机为研究对象，将悬架和轮胎视统一看作为弹性支座，忽略其各自阻尼，不考虑车架变形的影响因素[3]，同时进一步考虑了九轴全地面起重机在通过地面凸起时对车辆轴荷在分配的影响，建立了新的计算模型，对某九轴全地面起重机的各轴轴荷进行计算，并采用ANSYS对模型的计算结果进行了对比分析。使用MATLAB分析了轴距、悬架刚度、路面凸起高度对轴荷分配的影响。

1 某九轴全地面起重机轴荷计算模型的建立

假设该全地面起重机的车架为刚性体，由于悬架和轮胎的弹性刚度较小，所以可以将车架与各轴悬架和轮胎组成的弹簧单元看作一个多弹簧并联的多弹簧质量系统。各轴车下的质量为mw表示，根据车辆的特性各车下质量mw可看作相等。该系统中全车质量集中于质心，车架的变形绕瞬时中心O转动，且悬架和轮胎的变形为线性的[4-8]。

采用力学的方法建立并计算该弹性支座刚性模型，由图1所示，设各弹簧的变形分别为f1，f2，f3…f9，质心下降为f；由于各车下质量mw相等，所以在计算时不予考虑。1、2、3…9轴至1轴轴心的距离定义为L1(L1= 0 )L2、L3…L9，质心至1轴的距离定义为L；各悬架弹簧和轮胎的综合刚度分别为k1、k2、k3…k9；地面对各桥的支反力分别为Y1、Y2、Y3…Y9[5].地面支反力Y在数值和各轴轴荷是相等，所以求出各轴的支反力即可得到各轴轴荷。

计算时，车辆处于静止状态，所以由该模型的力矩平衡关系，得:

(1)

由垂直地面方向的受力平衡，可得:

(2)

由几何关系可得:

图1 多弹簧质量计算模型

(3)

(4)

悬架和轮胎组成的弹簧单元的变形是线性的，则:

Yi=kifi

(5)

由上述公式可得:

(6)

由上式可以看出，影响轴荷分配的主要是各轴轴距、弹簧刚度以及质心位置，并没有考虑到车辆过凸起时对车辆轴荷分配的影响。

图2所示，为车辆过凸起时的简化示意图，图中a为各轴过凸起时抬高的水平高度。

图2 车辆过地面凸起示意简图

由图2和式(5)可得:

Yi=ki(fi+ai)

(7)

由式(1)、式(2)、式(3)、式(4)、式(7)可得：

(8)

通过式(8)可以看出，车辆轴荷的分配与轴距、悬架弹簧刚度、轮胎刚度和各桥过路面凸起高度以及质心位置有重要关系，式(8)即为本文建立的轴荷计算模型。

2 模型计算结果与仿真结果的对比

采用有限元方法进行仿真计算对给出的计算模型的计算结果进行对比。该型全地面起重机车辆的基本参数见表1.

表1 某全地面(九轴)起重机基本参数

以有限元方法进行建模，采用梁单元Beam3来分别模拟车、轮胎与悬架的综合刚度，如图3所示。

图3 车轴轴荷计算有限元模型

车架杨氏模量(E)设为2.1×1010MPa(N/mm2)，用来杨氏模量来模拟各车轴悬架的等效刚度，各轴杨氏模量见表1.在9个弹簧10、11、12…18节点底部施加垂向约束，在19节点(质心)位置施加纵向约束，并施加垂向载荷P=G=958 491 N来模拟车辆总重量，以节点10、11分别抬高82 mm和150 mm，模拟前桥过凸起。

有限元方法的计算结果与本文模型计算结果的对比分析，见表2。

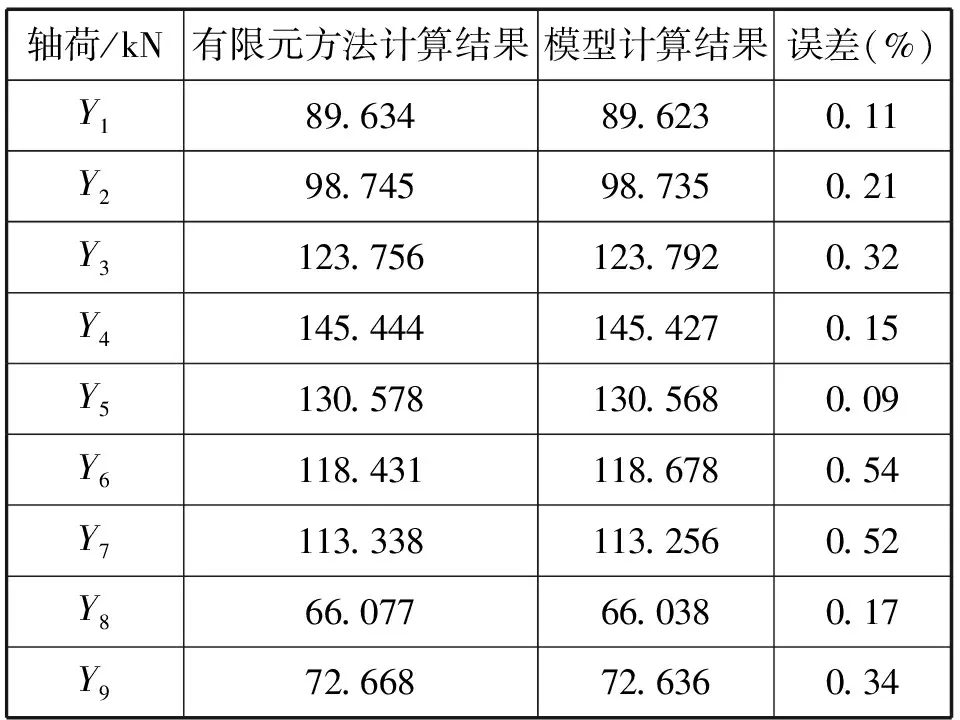
表2 车辆轴荷计算结果误差分析

从表2中的数据可以看出，有限元仿真结果与本文给出的计算模型计算相差范围不大，说明了本文给出的计算模型具有合理性。

3 轴荷分配影响因素分析

3.1 轴距变化对轴荷分配的影响

由于该全地面起重机的的车桥较多，所以只选取对轴荷分配影响较具代表性的第2轴和第5轴进行分析，因为2轴和5轴的图像变化较其他各轴复杂，变化趋势能够很好的代表其他各轴。图4和图5分别表示为第2轴和第5轴的轴距变化对各桥轴荷分配的影响。

第2轴距第1轴的距离为L2=1 480 mm，第2轴的初始位置。从图4可以看出，当2轴轴距变大时，即第2轴向第3轴方向移动时，第1轴轴荷的增大比较明显，而第4轴和第7轴正相反，呈明显的减小的趋势变化；第5轴和第3轴只是略有增长。当L2≤5 500 mm时，第2轴轴荷基本不变，第9轴轴荷缓慢减小，但是当L2≥5 500 mm-1时，第2轴轴荷开始慢慢减小，而第9轴轴荷趋于不变。

第5轴距第1轴距离为L5=6 540 mm，第5轴的初始位置。从图5可以看出，当第5轴向第6轴方向移动时，第1轴、第2轴和3轴的轴荷同时增大；第5轴、第8轴和第9轴的轴荷同时减小，且变化趋势十分明显；第6轴和第7轴轴荷基本不变。当5轴向4轴方向靠近时，第1轴、第2轴、第3轴和第5轴明显的减小，9轴则随之不断变大。

在L5=6 450 mm时，第1轴轴荷和第2轴荷相等，当L5继续变大时1轴轴荷大于第2轴轴荷，且相差越来越大。当L5<6 540 mm时，第2轴轴荷大于1轴轴荷，相差也是越来越大。

综合第2轴和第5轴轴距变化对各轴轴荷的影响可以看出，其中一轴的轴距变化对各轴轴荷变化都有影响，具体变化应具体分析。

3.2 弹簧刚度对轴荷分配的影响

在分析车轴刚度对车辆各轴轴荷分配影响时，依然只选取了具有代表性的第4轴和第8轴进行分析。图6和图7分别表示是第4轴和第8轴弹簧刚度变化对各轴轴荷分配的影响。

图6(a) 第4轴弹簧刚度对非相邻轴轴荷的影响

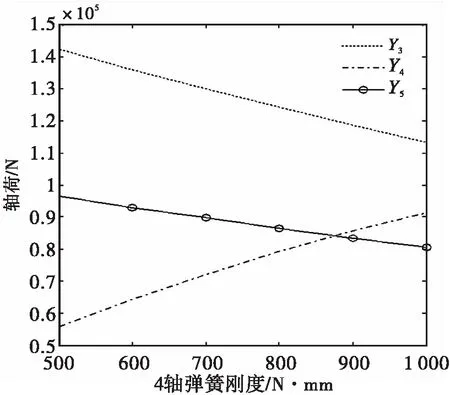
图6(b) 第4轴弹簧刚度对相邻轴轴荷的影响

从图6(a)中可以看出，随着第4轴弹簧刚度的不断增加，第8轴和第9轴的轴荷基本没有变化，比较稳定；第1轴、第2轴、第6轴和第7轴的轴荷不同程度的减小，但是减小范围都在10%以内。图6(b)中，随着第4轴弹簧刚度的增大，第3轴和第5轴的轴荷明显减小，减小范围都在20%以上。

由图7(a)中可以看出，随8轴弹簧刚度的增加，第7轴和第9轴的轴荷都随之减小，两轴减小的范围都在20以上，其中第9轴轴荷减小范围甚至接近40%.但是从图7(b)中看出，第8轴弹簧刚度的增加对其他各轴的影响要小的多。

综上所述，其中一轴的弹簧刚度的变化，对相邻各轴轴荷分配的影响比较大， 且变化趋势呈相反的规律，但对其它轴荷影响相对较小。

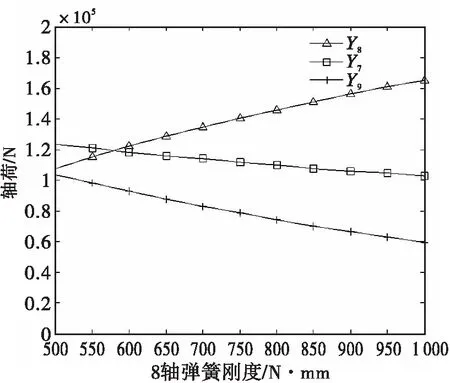
图7(a)第8轴弹簧刚度对后三轴轴荷的影响

Fig.7(a) 8thaxisspringstiffnessaffectaftertriaxialaxleweight

图7(b) 第8轴弹簧刚度对前六轴轴荷的影响

3.3 车辆过凸起时对轴荷分配的影响

在研究车辆过凸起时，选取了第3轴、第4轴和第5轴同时过凸起的情况，并以第5轴为例详细分析了车辆过凸起对车辆的各轴轴荷再分配的影响。

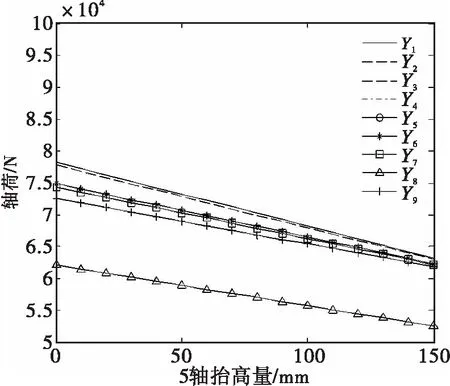
图8(a) 第5轴过凸起对不过凸起轴轴荷的影响

图8(b) 第5轴过凸起对过凸起轴轴荷的影响

从图8的(a)、(b)两图可以看出，当第5轴的抬高量变大时，第5轴轴荷随之增大非常明显，其余各轴轴荷都呈减小的趋势。

4 结论

(1)通过与有限元仿真计算结果的对比，说明了本文给出的计算模型具有合理性，该计算模型物理意义明确，公式简洁。

(2)各轴轴距变化对车辆各轴轴荷分配都有影响；弹簧刚度对相邻的轴的轴荷影响最大，且变化趋势与之呈相反的规律；车辆过地面凸起时过凸起的轴轴荷明显变大，而其余各轴轴荷则出现不同程度的减小。

参考文献：

[1] 余志生.车辆理论[M].第2版.北京：机械工业出版社，1998 ：67-68.

[2] 徐继，顾严平，彭莫.多轴汽车的特性参数[J].车辆工程，1996，18 (1)：20-25.

[3] 王国军，祁涛，陈欣，等.多轴汽车轴荷的合理分配与确定[J].军事交通学院学报，2009，11(2)：53-56.

[4] 王国军，陈欣，徐安桃，等.某重型高机动越野汽车轴荷计算与试验[J].军事交通学院学报，2012，14(1)：54-56.

[5] 龙驭球.结构力学(上册)[M].北京：高等教育出版社，1994：254-427.

[6] 智常建，张小平，肖利，等.解析刚度理论在板形控制中的应用[J].太原科技大学学报，2011，32(1)：22-26.

[7] 李扬 ，卫良保.基于VC和MATLAB的单梁起重机主梁优化设计[J].太原科技大学学报，2012，33(1)：33-37.

[8] 李宏娟，陶元芳.桥门机主梁设计时强度与刚度的关系[J].太原科技大学学报，2011，32(1)：40-44.