AZ31镁合金热变形过程中的流变应力

王 庆，林金保，黄庆学，王 翀(太原科技大学，太原 030024)

镁及镁合金是在工程应用中最轻的金属结构材料[1]。镁合金具有比强度、比刚度高以及良好减振性、切削加工尺寸稳定等优点，尤其易于回收利用，具有环保特性[2]，在实际生产应用中具有广阔的应用前景。研究AZ31镁合金在高温下的塑性变形为与该合金在高温塑性变形过程中的真应力真应变，为制定AZ31镁合金热加工过程的工艺参数提供理论参考，为研究AZ31镁合金的热变形理论和塑性变形的数值模拟提供必要的实验数据。

1 材料及试验方法

实验的材料为商用的AZ31镁合金，为Mg-Al-Zn系合金，其化学成分(质量分数)为：Al 2.5%-3.5%，Zn 0.6-0.4%，Mn 0.15-0.5%，Ca 0.05%，Ni 0.005%，Fe 0.005%，Mg余。将材料通过线切割机床加工成Φ8×12 mm圆柱式实验试样，在Gleeble 1500热模拟试验机上对试样进行单向热压缩实验。压缩温度为473 K-673 K，温度间隔为50 K，应变速率为0.005 s-1、0.05 s-1、0.5 s-1、3 s-1.压缩前温升速度为4 K/s，到额定温度后保温5 min.试样相对压下量为60%.

材料按照国标加工成如图1所示的拉伸试样，在UTM5305拉伸机上进行单向拉伸。实验温度与压缩相同，应变速率分别为0.000 33 s-1，0.001 s-1，0.01 s-1，0.05 s-1.拉伸前温升速度为5 K/s，到温后保温10 min.

图1 热拉伸试样标准尺寸

2 实验结果分析

2.1 真应力真应变曲线对比

如图2、3所示为AZ31镁合金在不同应变速率和不同温度下热变形的真应力-真应变曲线。AZ31镁合金在热变形过程中的真应力峰值随应变速率变化而变化，表明该合金材料是应变速率敏感材料。在压缩变形过程中AZ31镁合金的真应力先升高至峰值然后降低至稳态值。在拉伸变形过程中AZ31镁合金的真应力值不断增加，直至试样拉断。由于镁合金为密排六方晶体结构的金属材料，所以在压缩拉伸热变形过程中镁合金的真应力明显不同。在高温低速的变形过程中AZ31镁合金的真应力峰值消失。无论是在压缩还是拉伸过程中，真应力都出现明显的锯齿形波动，说明在镁合金在热变形过程中存在动态回复。

图2AZ31镁合金热压缩变形过程中的真应力应变曲线

Fig.2Thetruestress-straincurveofAZ31Magnesiumalloyduringthermalcompressionprocess

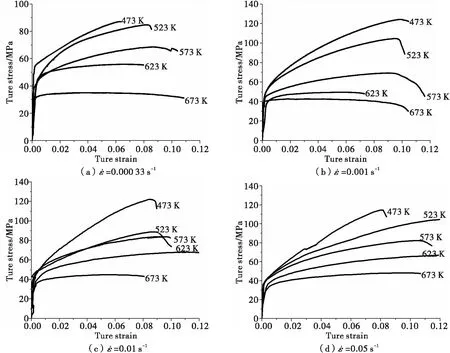
图3 AZ31镁合金热拉伸变形过程中真应力应变曲线

2.2 应变速率对真应力的影响

(1)

其中，s1和n1均为材料的常数，而在低温、高速的变形条件下该合金的真应力与应变速率之间的关系可用幂指数关系描述:

(2)

式中，s2和β是材料常数。由于方程(1)仅适用于低应力水平和式(2)仅适用于高应力水平的局限性，本文采用了包括变形激活能Q和温度T的修正后的双曲正弦形式Arrhenius关系来描述AZ31镁合金的热变形行为[4-6]:

(3)

其中s，n与α是材料常数，R是气体常数。由于式(3)可以同时描述AZ31镁合金变形过程中的低应力和高应力，因而该式可用于描述不同变形条件下AZ31镁合金的应力应变关系。材料常数α，β与n之间满足:

α=β/n

(4)

由于AZ31镁合金材料易发生动态回复，因此选用该材料的峰值应力值来描述变形过程中的真应力，假定在温度确定时，该材料的变形激活能为一常数，则由式(1)～式(3)推导得:

(5)

(6)

(7)

图4AZ31镁合金压缩变形过程中的真应力峰值与应变速率之间的关系

Fig.4TherelationshipbetweenthetruepeakstressandstrainrateduringAZ31magnesiumalloycompressiondeformationprocess

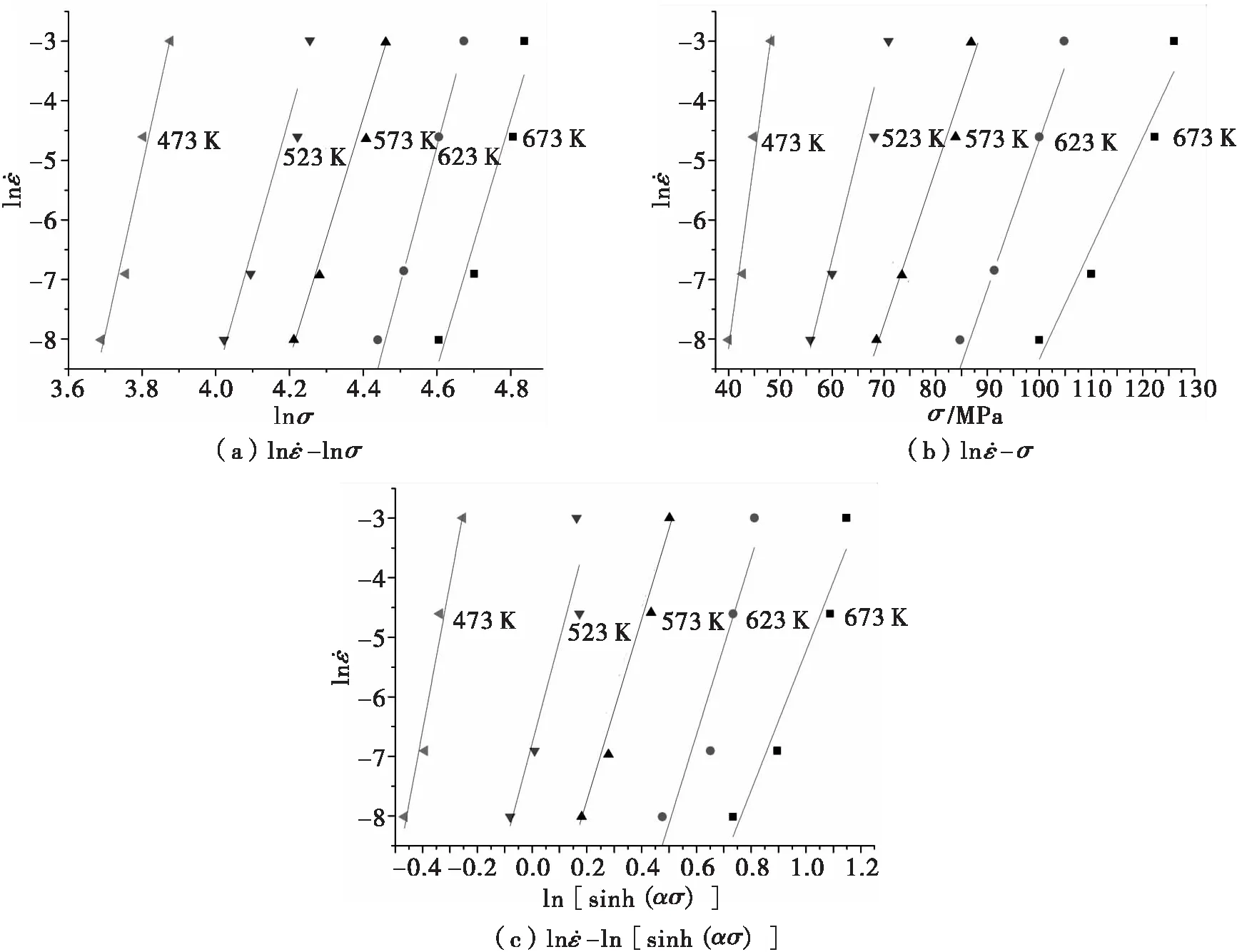
图5 AZ31镁合金拉伸变形过程中的真应力峰值与应变速率之间关系

图5分别为在不同变形条件下AZ31镁合金热变形时应变速率与真应力峰值之间的关系曲线。通过实验数据分析，发现在变形温度确定时，真应力峰值与应变速率之间的线性关系比较明显。

根据对试验数据的拟合，可得热压缩过程中的n1=14.159 9和β=0.125 5，从而根据式(4)得到α=0.008 9 MPa-1.热拉伸过程中的n1=22.67和β=0.336 2，得到α=0.014 8 MPa-1采用实验数据求得的α值，重新绘制真应变真应力的双曲正弦关系图，从拟合图4(c)、5(c)来看，应变速率与真应力峰值符合线性关系。当变形温度上升时，直线斜率会随温度的变化而变化，也说明变形激活能不是随温度变化而不变。

2.3 变形温度对真应力的影响

AZ31镁合金在变形过程中的真应力，通常由AZ31镁合金在不同变形温度、变形速率和变形程度下，热变形过程中的峰值应力值的大小来衡量。由定义Zener-Hollomon的参数，可以得到:

(8)

当应变速率确定并保持不变时，假定变形温度在小范围内变化时AZ31镁合金的变形激活能保持不变，对方程(8)取对数可得:

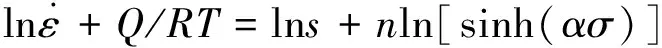
(9)

由此可得峰值应力与温度之间的关系:

(10)

图6所示为根据实验温度和真应力峰值绘制得到的ln[sinh(ασ)]-1 000/T之间的曲线关系。如图6可知，变形温度和真应力峰值呈较好的线性关系，由此证明AZ31镁合金在热变形过程中变形温度和真应力峰值之间满足Arrhenius曲线关系，可以用Z参数来描述AZ31镁合金在热变形过程中时的真应力真应变行为。

图6AZ31合金的ln[sinh(ασ]与103/T的关系

Fig.6Therelationshipbetweenln[sinh(ασ)]and103/TofalloyAZ31

2.4 流变应力方程的建立

变形激活能是受AZ31镁合金材料组织结构及变形过程中的工艺参数等不同的变形因素的影响，是描述AZ31镁合金在高温变形过程中重排原子的难易程度的一个微观物理量。变形速率减小时，合金内位错迁移速率的升高导致位错密度减小，使位错的滑移不受阻，不会引起晶界附近的应力集中，从而降低材料的变形激活能[11]。

由于变形温度和应变速率对AZ31镁合金的变形激活能有直接影响，利用式(3)可得：

(11)

由式(8)可推出：

sinh(ασ)=(Z/s)1/n

(12)

由定义双曲正弦函数推导得:

sinh-1(ασ)=ln[ασ+(ασ2+1)1/2]

(13)

由此，可将真应力表示成参数Z的函数：

σ=1/αln{(Z/s)1/n+[(Z/s)2/n+1]1/2}

(14)

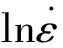
根据式(8)，得到压缩、拉伸参数Z分别为：

Z=εexp[132.28×103/(RT)]
Z=εexp[255.26×103/(RT)]

根据式(3)，得到该合金的流变应力方程分别为：

ε=7.01×1020[sinh(0.0089σ)]9.664·
exp[-132.38×103/(RT)]
ε=5.54×1034[sinh(0.0148σ)]15.8·
exp[-255.26×103/(RT)]

根据式(14)，热变形流变应力方程分别为：

σ=112.359ln{[Z/(7.01×1020)]1/9.664+
[(Z/(7.01×1020))2/9.664+1]1/2}
σ=67.567ln{[Z/(5.54×1034)]1/15.8+
[(Z/(5.54×1034))2/15.8+1]1/2}

3 结论

(1)AZ31镁合金在473-673K进行热变形时，应变速率和变形温度对真应力产生明显影响。AZ31镁合金在变形过程中真应力峰值随温度、应变速率的变化而变化。在高速低温的变形情况下，热拉伸AZ31镁合金的真应力值不断增加，不存在稳态应力值。在低速高温的变形情况下AZ31镁合金变形过程中的真应力峰值消失。在压缩拉伸的热变形过程中AZ31镁合金的真应力明显不同。无论是在压缩还是拉伸变形过程中，真应力都出现明显的锯齿形波动，说明在AZ31镁合金的热变形过程中存在动态回复。

(2)AZ31镁合金热变形的真应力行为可用包含Arrhenius项的Zener-Hollomon 参数来描述。该合金的热变形激活能：压缩变形激活能为Q=132.38 kJ/mol，拉伸变形激活能为Q=255.26 kJ/mol，热压缩变形的真应力方程为：

ε=7.01×1020[sinh(0.0089σ)]9.664×

exp[-132.38×103/(RT)]

热拉伸变形的真应力方程为：

ε=5.54×1034[sinh(0.0148σ)]15.8×

exp[-255.26×103/(RT)]

参考文献：

[1] FROES F H，ELIEZER D，AGHION E.The science technology and applications of magnesium[J].JOM，1998(9)：30-33.

[2] 曾小勤，王渠东，吕宜振，等.镁合金应用进展[J].铸造，1998(11)：39-43.

[3] 黎文献，杨军军，肖于德.Al-Fe-V-Si 合金高温变形热模拟[J].中南工业大学学报，2000，31(1)：56-59.

[4] RYAN N D，MCQUEEN H J，EVANGELISTA E.Dynamic recovery and strain hardening in the hot deformation of type 317 stainless steel[J].Mater Sci Eng，1986，81：259-272.

[5] MCQUEEN H J，RYAN N D.Constitutive analysis in hot working[J].Mater Sci Eng，2002，A322：43-63.

[6] GUO J，CHEN L，XU Y，et al.Investigation of the compressive creep behavior of AZ91D magnesium alloy[J].Mater Sci Eng A，2007，443：66-70.

[7] AGNEW S R，TOMÉ C N，BROWN DW.Study of slip mechanisms in a magnesium alloy by neutron diffraction and modeling [J].Scripta Materialia，2003，48：1003-1008.

[8] AGNEW S R，DUYGULU O.A mechanistic understanding of the formability of magnesium：examining the role of temperature on the deformation mechanisms [J].Materials Science Forum，2003，422：177-188.

[9] AGNEW S R，BROWN D W，TOME C N.Validating a polycrystal model for the elastoplastic response of magnesium alloy AZ31 using in situ neutron diffraction [J].Acta Materialia，2006，54：4841-4852.

[10] BARNETT M R，KESHAVARZ Z，MA X.A semianalytical Sachs model for the flow stress of a magnesium alloy [J].Metallurgical and materials transactions A，2006，37：2284-2293.

[11] MWEMBELA A，KONOPLEVA E B，JMCQUEEN H.Microstructural development in Mg alloy AZ31 during hot working[J].Script Mater，1997，37：1789-1795.