前半球中距攻击的轨迹优化方法*

赵 雨，张 斌，隋永华，李浩亮

（空军工程大学航空航天工程学院，西安 710038）

前半球中距攻击的轨迹优化方法*

赵 雨，张 斌，隋永华，李浩亮

（空军工程大学航空航天工程学院，西安 710038）

为了提升飞行员空战对抗能力，提出了前半球中距攻击轨迹优化方法。首先，建立了矢量方程，并分析了空战中几何态势。其次，综合考虑时间和角度优势，给出了最优轨迹的计算方法。最后，通过仿真实验给出了最优轨迹及相关飞行参数。仿真结果表明，该方法对于解决前半球中距攻击非常有效。

前半球中距攻击，最优轨迹，时间，角度优势

引言

在空战过程中，前半球中距攻击是一种常见的攻击方式，而攻击轨迹的选择对于我机顺利击毁目标并保证自己安全至关重要。大多数文献［1-2］是对地攻击轨迹规划，而对空前半球攻击的研究相对较少，其中文献［3］定性地分析了空战过程中的优势和威胁。本文分析了前半球攻击的空战态势，综合考虑了时间和角度优势，给出了一条优化的攻击轨迹。

1 问题的描述

为了研究方便，做以下假设：我机与目标在同一平面运动，双方速度为常数。战斗机攻击引导一般过程如图1所示。符号说明：W0、Wt与Wb分别为我机初始位置、攻击过程中我机的某一位置与我机武器发射时刻的位置；M0、Mt与Mb分别为目标与我机在W0、Wt与Wb位置时的对应位置；P为命中点。攻击轨迹优化的任务就是根据双方作战态势由战斗机的火力控制分系统确定出我机优化的操纵控制量，使我机能以某战术指标最优的方式达到武器发射条件。

图1 前半球攻击示意图

前半球攻击可分为拦射攻击和迎头攻击［4］。迎头攻击是指敌我相向飞行，目标做匀速直线运动。我机需要考虑如何做机动才能获得一定的角度优势。拦射攻击时，敌我以一定夹角相向飞行，目标做匀速运动。我机已经有了角度优势，重点考虑如何使攻击时间最短。下面就两种情况分别建模分析。

2 迎头攻击模型的建立和求解

2.1 解决思路

综合分析空战态势，建立矢量方程［5-6］。以目标线为基准，将矢量方程投影到基准线和垂直基准线的两个标量方程，联立解出需用过载n和飞行时间Tf。每一组n和Tf，对应着唯一的q和Tf。综合考虑q和Tf，建立目标函数，求出最优的攻击轨迹。

2.2 建立模型

图2 迎头攻击矢量图

符号说明：D0为我机与目标初始距离；Wa为我机转到初始航向角的位置；r为我机转动半径；η为我机初始航向角；Dd为武器最大有效射程；q为目标进入角；Ma为我机转动到初始航向角时目标位置；Vw为我机速度；Vm为目标速度；Tf为我机飞行时间；Td为武器飞行时间；T0为目标调整到初始航向角的时间；Rd静载体平台上的最大有效动力射程；n为我机过载；g为重力加速度；其他符号说明与图1相同。根据图2，建立以下矢量方程：

我机转动到初始航向角需要的时间:

在真实空战中，T0很小，所以不考虑该时间内我机位置变化，即W0与Wa为同一点，只考虑目标位置变化。

从初始点Wa到命中点P的位移：

矢量方程在基准线上的投影：

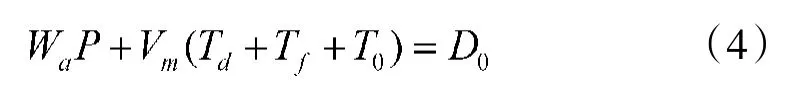
将式（2）、式（3）带入式（4）中得:

从初始点Wa到发射点Wb的位移：

目标进入角：

矢量方程在垂直基准线上的投影：

将式（6）、式（7）带入式（8）中得：

联立方程（5），方程（9），即可解出n、Tf。

2.3 模型的约束条件

在真实空战中，我机应该始终跟踪目标。所以我机机动时，目标不能超过雷达探测距离和角度的限制。通常，丢失目标是因为超过了最大探测角度。所以本文只对探测角度进行约束。假设我机最大探测角度为±ρmax。

式（10）～式（12）联立解出：

约束条件为：对于任意时刻t∈［0，Tf］，均应满足η≤ρmax。

2.4 目标函数求解

目标函数：

由于时间的数量级为几百秒，角度优势仅是一个0～1之间无量纲的数。上式中通过归一化处理，使二者对攻击轨迹具有相同的敏感度。α1、α2分别为时间和角度优势的权系数，可以根据专家评估来确定。Y是目标值，Y越大，则该条轨迹越优，反之，该轨迹越劣。

3 拦射攻击模型的建立和求解

3.1 解决思路

拦射攻击时与迎头攻击模型基本一致。不同点在于我机已经有了一定的角度优势，轨迹的选择对角度的影响不大，所以以时间最短为目标建立函数。

3.2 建立模型

图3 拦射攻击矢量图

图3中，ψ为我机提前角；D.为目标线线速度；ωG为目标线角速度；其他符号与图2中相同。建立矢量方程：

将方程分别投影到目标线和垂直目标线方向：

将式（18）、式（19）带入式（16）、式（17）中联立求解：

3.3 模型的求解

假设我机最大探测角度为±ρmax，模型的约束条件为：对于任意时刻t∈［0，Tf］，均应满足ψ≤±ρmax。在初始时刻，我机已经有了一定的角度优势，若再通过机动角度变化不明显，而时间变化明显。因此，本文以时间为目标函数，寻求最优轨迹。

4 仿真验证

假设空战条件如下:初始我机与目标距离120 km，我机速率320 m/s，目标速度300 m/s，武器最大飞行时间40 s，武器在静载体平台上最大有效射程20 km，我机最大过载4，载机最大探测角为60°。

4.1 迎头攻击仿真

在迎头攻击方式下，目标做匀速直线运动，敌我相向飞行。权系数的变化对最优轨迹选择的影响：权系数体现了对时间和角度优势的侧重程度，随着α1的增大，最优轨迹的时间减小，角度优势增大，如图4、图5所示。

图4 权系数与时间关系

图5 权系数与角度优势关系

在确定权系数的条件下最优轨迹的选择：假设时间权系数为0.4，角度优势权系数为0.6。

图6 迎头攻击轨迹包线

图7 迎头攻击最优轨迹

表1 迎头攻击最优轨迹参数表

4.2 拦射攻击仿真

除迎头攻击以外的前半球攻击均称为拦射攻击。此攻击方式对目标的任何机动均适用。为研究方便，假设目标做S机动。

最优轨迹及相关参数的计算：时间为唯一的目标函数，始终按照时间最短的轨迹向发射点飞行。图8中拦射轨迹与比例导引轨迹进行了对比，更有力地说明了前者时间更短。

图8 拦射攻击最优轨迹

图9 误差角变化图

图10 航向角变化图

表2 拦射攻击最优轨迹参数表

5 结 论

本文通过分析单机的前半球中距空战态势，建立了几何模型，从而解出了最优轨迹。迎头攻击要求敌我相向飞行且目标不机动，该模型适用性较弱；拦射攻击则对目标任何机动均适用。本文的分析有利于飞行员了解空战态势，进行辅助决策。该模型也可以推广到多对多空战，但需要考虑目标分配、协同作战等因素，有待于进一步研究。

［1］陈中起.空地多目标序贯攻击作战规划研究［D］.西安：空军工程大学，2008.

［2］范洪达，马向玲，叶 文.飞机低空突防航路规划技术［M］.北京：国防工业出版社，2007.

［3］蓝伟华，林南粤.单机对单机交战几何态势分析［J］.电光与控制，2004，11（4）：14-16.

［4］寇英信，张 斌.作战飞机引导控制原理［M］.西安：空军工程大学，2009.

［5］姚佩阳，薛艺莉，王冬旭.迎头抢攻飞行轨迹数学建模及评估［J］.空军工程大学学报（自然科学版），2010，11（2）：6-10.

［6］陈中起，张 斌，杜永伟，等.近距引导战斗机自动攻击控制律实现［J］.火力与指挥控制，2012，37（5）：148-151.

［7］周志刚.航空综合火力控制原理［M］.北京：国防工业出版社，2008.

A Study on Method of Trajectory Optimization for Forward Hemisphere Mid-range Attack

ZHAO Yu，ZHANG Bin，SUI Yong-hua，LI Hao-liang
（School of Aeronautics and Astronautics Air Force Engineering University，Xi'an 710038，China）

In order to enhance against capability of pilots in air combat，the method of trajectory optimization for forward hemisphere mid-range attack is proposed.Firstly，the vector equation is built up，and the geometry of air combat is analyzed.Then，considered in time and angle advantage，the method of calculating trajectory optimization is proved.Finally，the best trajectory and interrelated parameters are given by simulation.The result shows that this method is very effective for forward hemisphere mid-range attack.

forward hemisphere mid-range attack，trajectory optimization，time，angle advantage

V212.1

A

1002-0640（2014）09-0044-04

2013-06-16

2013-09-19

航空科学基金资助项目（20095196012）

赵 雨（1989- ），男，河南安阳人，硕士研究生。研究方向：航空火力指挥与电子综合。