螺形映照几个扩充子族的一种构造方法

刘爱超,葛立

（1.黄淮学院数学系,河南驻马店463000；2.河南科技学院,河南新乡453003）

螺形映照几个扩充子族的一种构造方法

刘爱超1,葛立2

（1.黄淮学院数学系,河南驻马店463000；2.河南科技学院,河南新乡453003）

在复Cn空间的单位球Bn上已经有了星形映照、螺形映照的3个扩充子类：α次殆β型螺形映射、α次β型螺形映射、α次强β型螺形映射,但这3个子类存在支持不够充足.以复分析和泛函分析为工具,在Reinhardt域Ωp1…pn上给出了这3种子类的一种构造方法,该结论对单位球Bn同样成立.

α次殆β型螺形映射；α次β型螺形映射；α次强β型螺形映射；构造

单复变几何函数论中的例子一般而言都是大量存在的,但当空间的维数n＞1时,星形映射和螺形映射及其子族的映射都很少.为此,Roper K A R和Suffridge T J引入Roper-Suffridge算子,利用该算子可以构造高维空间螺形映照和星形映照及其子族.随后Graham I等在Roper-Suffridge算子上又做了很多工作[1-3].当今利用Roper-Suffridge算子构造高维空间的映照已成为多复变几何函数论研究的热点之一.目前,国内这方面也展开了一些研究,并取得一系列可喜的成果[4-5].且高维空间映照的构造研究仍在不断深入[6-8].

在参阅文献[4]、[5]的基础上,本文在Reinhardt域Ωp1…pn给出了次殆型螺形映射、次型螺形映射、次强型螺形映射的一种构造方法.

1 预备知识

文献[4]中,Cn中的单位球Bn已经有了星形映照、螺形映照的3个扩充子类：α次殆β型螺形映射、α次β型螺形映射、α次强β型螺形映射的定义.3种定义中,只需将用代替,即得Ωp1…pn上相应的3种定义.文中不再赘述.

当n=1时,有相应的单位圆盘D上α次殆β型螺形函数、α次β型螺形函数、α次强β型螺形函数的定义.

文献[4]中还给出了3个对应的例子,说明单位圆盘D上α次殆β型螺形函数、α次β型螺形函数、α次强β型螺形函数确实是存在的.

引理1[10]设ρ(z )是Ωp1…pn的Minkowski泛函,,则

引理2设fj(z)(1≤j≤n)为单位圆盘D上正规化双全纯函数,且

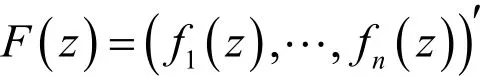
则

证明：由引理1进行简单计算可得.

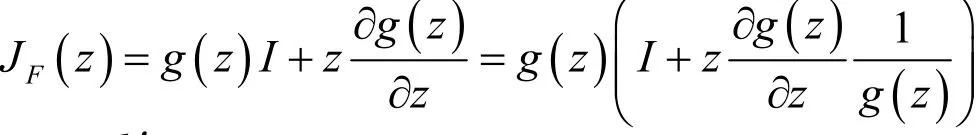
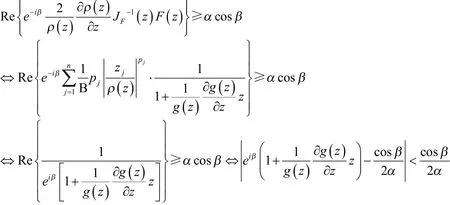
2 主要结果与证明

定理1若fj(z)(1≤j≤n)为单位圆盘D上正规化α次殆β型螺形函数,则为Ωp1…pn上α次殆β型螺形映射

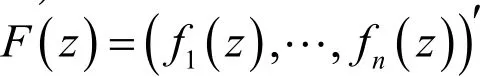
因而F( z)=(f(z),…,f(z))′为Ω上α次殆β型螺形映射.

1n

定理2若fj(z)(1≤j≤n)为单位圆盘D上正规化α次殆β型螺形函数,λj≥0满足,则为Ω上α次殆β型螺形映射.p1…pn

证明：仅讨论α≠0的情形,α=0时结论显然成立.令

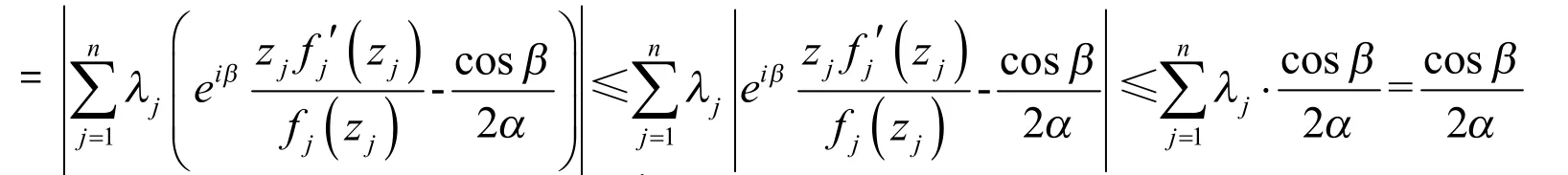
定理3若fj(z)(1≤j≤n)为单位圆盘D上正规化α次β型螺形函数,则 F( z)=(f1(z),…,fn(z))′为Ωp1…pn上α次β型螺形映射.

因而为Ωp1…pn上α次β型螺形映射.

定理4若fj(z)(1≤j≤n)为单位圆盘D上正规化α次强β型螺形函数,则F( z)=(f( z),…,f(z))′

1n为Ωp1…pn上α次强β型螺形映射.

证明：由引理2知

注记：在域Ω上,当p1=p2=…=pn=2时,此时泛函ρ(z)=z,上述各定理即成为Cn中的单位球Bn上的相应结论或文献[4]中的结论.

定理5设F( z)为单位圆盘D上正规化α次强β型螺形函数,则

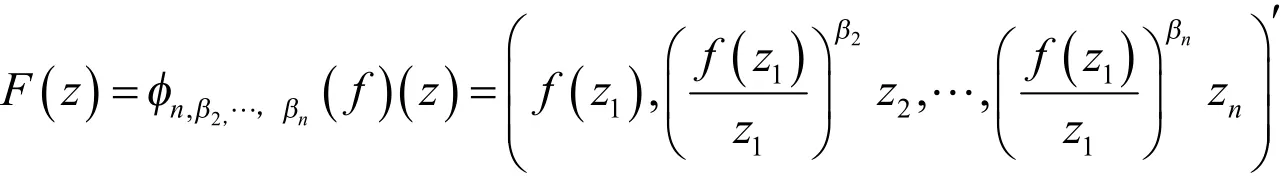
证明：结合引理1及文献[11]有

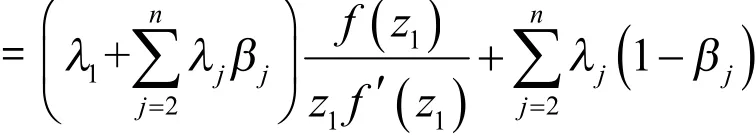
从而

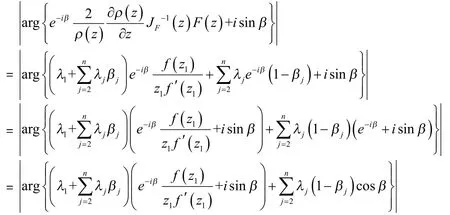
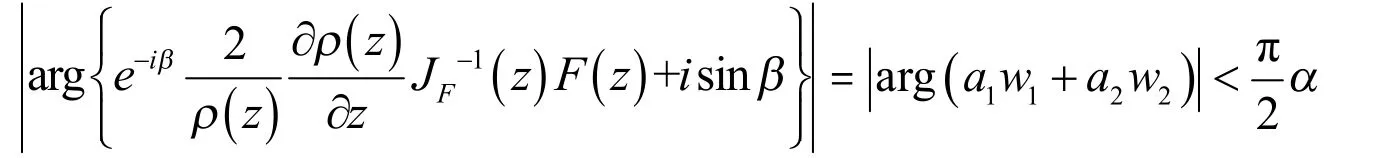
或F( z)为域Ωp1…pn上的α次强β型螺形映射.

当β=0时,即得域Ωp1…pn上α次强星形映射的结论

注记1：当p1=2,即得算子

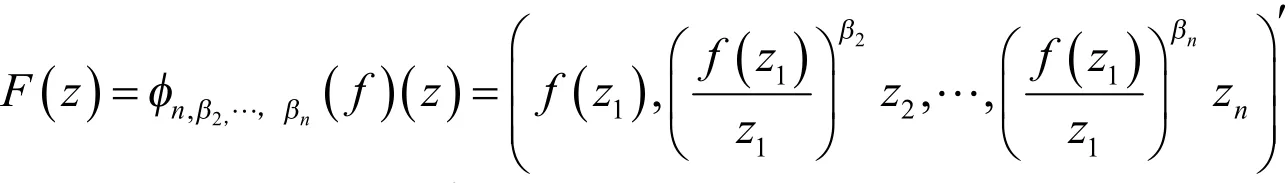
注记2：当p1=…=pn=2,β2=…=βn时,本定理即为Cn中的单位球Bn上的结论,文中不再赘述.

3 小结

自Roper-Suffridge算子出现以来,许多学者都对其做了很多研究,从而在不同域上引申出不同形状的Roper-Suffridge算子.在参考诸多文献的基础上,文章结合Roper-Suffridge算子在Reinhardt域Ωp1,…,pn上给出了α次殆β型螺形映射、α次β型螺形映射、α次强β型螺形映射的一种构造方法,从而为他们的存在性提供了实例.

[1]Graham I,Kohr G,Kohr M.Lowner chains and the Roper-Suffridge extension operator[J].Journal of Mathematical Analysis and Applications,2000,247（2）：448-465.

[2]Graham I,Kohr G.Univalent mappings associated with the Roper-Suffridge extension operator[J].Journal d’Analyse Mathématique,2000,81（1）：331-342.

[3]Graham I,Hamada H,Kohr G,et al.Extension operator for locally Univalent mappings[J].Michigan Mathematical Journal,2002,50（1）：37-55.

[4]冯淑霞.多复变数的几类全纯映照族[D].合肥：中国科学技术大学,2004.

[5]刘小松.多复变函数几何函数论中某些映照子族的性质[D].合肥：中国科学技术大学,2004.

[6]刘名生,朱玉灿.有界完全Reinhardt域上推广的Roper-Suffridge算子[J].中国科学A辑：数学,2007,37（10）：1193-1206.

[7]刘名生,朱玉灿.在Banach空间上推广的Roper-Suffridge算子（Ⅲ）[J].中国科学A辑：数学,2010,40（3）：265-278.

[8]朱玉灿,刘名生.在Banach空间上推广的Roper-Suffridge算子（Ⅰ）[J].数学学报：中文版,2007,50（1）：189-196.

[9]Taylor A E,Lay D C.Introduction to functional analysis[M].New York：John Wiley and Sons,1998.

[10]Liu T S,Zhang W J.On decomposition theorem of normalized biholomorphic convex mappings in Reinhardt domains[J].Science in China,Sect.A,2003,46（1）：94-106.

[11]Feng S X,Liu T S.The generalized Roper-Suffridge extension operator[J].J.Acta Mathematica Scientia,2008,28B（1）：63-80.

（责任编辑：卢奇）

A construction method of some subclasses of spirallike mappings

Liu Aichao1,Ge Li2
（1.Department of Mathematics,Huanghuai College,Zhumadian 463000,China；2.Henan institute of science and techonology,Xinxiang 453003,China）

Three subclasses of starlike mapping and spirallike mapping have also existed on unit ball in complex space,which were almost spirallike mappings of type β and order α,spirallike mappings of type β and order α,strongly spirallike mappings of type β and order α respectively,but the existence is not enough for these three subclasses. Using complex analysis and functional analysis,a kind of constructive method for the there subclasses was given.The same conclusion is true for unit ball Bn.

almost spirallike mappings of type β and order α；spirallike mappings of type β and orderα；strongly spirallike mappings of type β and order α；construction

O174.5

A

：1008-7516（2014）01-0043-06

10.3969/j.issn.1008-7516.2014.01.009

2013-10-22

河南省计划项目（112300410251）

刘爱超（1979-）,男,河南新郑人,硕士,讲师.主要从事多复变函数论研究.