均匀布筋的双偏压矩形柱简化设计

马泽峰 陆洲导 许建立 蔡兹红

（1.同济大学结构工程与防灾研究所，上海200092；2.上海建筑设计研究院有限公司，上海200041）

均匀布筋的双偏压矩形柱简化设计

马泽峰1，2*陆洲导1许建立2蔡兹红2

（1.同济大学结构工程与防灾研究所，上海200092；2.上海建筑设计研究院有限公司，上海200041）

在荷载等值线法的基础上，考虑均匀配筋形式，通过大量变参数、多水平的数值运算，拟合双偏压钢筋混凝土矩形柱截面轴压比与无量纲弯矩等值线的相关指数的函数关系，以及两主轴方向轴压比与无量纲参数˜m的关系曲线。基于所得强度曲线提出简化计算方法，并通过试验验证。给出算例以明确应用过程。提出的简化方法具有精度高、运算快的优点，可用于实际的工程设计。

双偏压，荷载等值线法，无量纲，相关指数

1 引 言

承受轴力及双向弯矩的柱构件普遍存在于建筑结构中。典型的是框架结构的角柱、纵向柱列较少的房屋、管道支架和水塔的支柱等。即便是边柱或中柱，也会由于相邻跨跨度的差异以及荷载分布的不均匀而处于双偏压受力状态。研究表明，影响双偏压柱截面强度的因素主要有轴压比（n）、混凝土和钢筋的强度（fc，fs）及本构关系、纵筋配筋率（ρ）、纵筋的布筋形式、截面尺寸（H高，B宽）、保护层厚度及偏心角度（θ）等［1］。以往针对双偏压柱的研究主要考虑的是普通强度混凝土（NSC），对现代高层建筑中普遍采用的高强混凝土（HSC）方面内容却涉及较少。另外，截面的高宽比（SR＝H／B）影响的研究也集中在SR∈［1，2］的区间，对SR∈（2，4］的扁柱强度特点的研究成果几乎没有。

经典的研究双偏压截面强度的思路主要有两种，一种是精确化方法，另一种是近似化方法。精确化方法也可称为一般化方法，根据处理思路的不同又可分为纤维积分法和等效矩形应力图法。纤维积分法的假定少，适应性强，精度高，同时需要大量的迭代运算，耗费计算资源，应用复杂。许多学者［2，3］对纤维积分法进行简化，手段主要是通过减少受压混凝土的积分块数，增加单块范围内的积分点数，尽量在一定精度范围内减少运算次数，提高迭代效率。

近似化方法就是对双偏压强度面的近似。我国《混凝土结构设计规范》（GB 50010—2010）采用的是倪克勤（N.V.Nikitin）公式。这种方法是用平面来近似模拟强度面，是弹性阶段的应力叠加法，实际是一种容许应力法，这种设计思路与我国规范普遍采用的极限强度法不同，相对落后，按此方法计算的强度面也偏保守。美国规范ACI 318—05［4］推荐的布雷斯勒（Bresler）荷载倒数法，从破坏面上点与近似平面上点的距离角度推导出与倪克勤公式实际相同的形式。这种方法更方便用于验证，而很难用于实际设计。

布雷斯勒建议的另一种近似方法，既荷载等值线法也被美国规范ACI 318—05［4］及欧洲规范EN 1992-1-1：2004［5］采用。按这种方法，给定轴力N作用下的强度面可由式（1）的无量纲形式近似表示：

另外，随着现代混凝土技术的发展，高强混凝土（HSC）广泛用于实际工程。高强混凝土材料强度高，延性差，变形能力弱，其力学性质不能简单地由普通混凝土（NSC）外推获得。前述针对普通混凝土双偏压强度研究的成果用于高强混凝土时，必然需经过修正。

截面的高宽比（SR）是矩形截面柱的主要形状参数，随高宽比的增加，构件由正常柱过渡为扁柱，两方向尺寸差别逐渐加大，必然会对极限强度造成一定影响。

本文的主要工作是基于纵筋均匀配置的布筋方式，考察轴压比、混凝土和钢筋的强度及本构关系、纵筋配筋率、截面高宽比等因素对双偏压荷载作用下截面强度破坏面的影响。经过大量数值计算，回归无量纲参数与强度破坏面的函数关系，提出近似强度面的拟合公式，并将公式直接用于工程设计。

2 分析基础

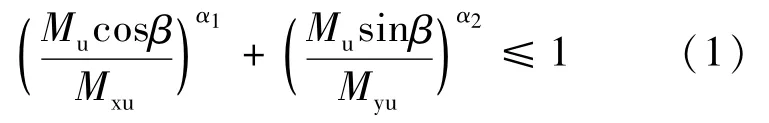
式中，Mxu，Myu为给定轴力下，截面绕x轴和y轴的极限弯矩；α1，α2为与前述截面强度影响因素相关的指数。

这种破坏面的表达形式在实际设计中仍较难应用，不过更接近真实的强度破坏面，更符合现阶段规范的极限设计思路。布雷斯勒的分析和试验工作主要偏重于荷载倒数法，对于荷载等值线法，仅给出公式，并没有对指数取值进行细化，建议取α1＝α2∈［1.15，1.55］。

许多学者［6，7］在荷载等值线公式基础上，对指数α1，α2的取值进行了深入研究。提出了不同的取值简化计算方法。欧洲规范EN 1992-1-1：2004［5］给出的指数α1＝α2＝a为：对于圆形和椭圆形，a＝2；对于矩形a取值见表1。

2.1 基本假定

数值模拟采用查德维尔（Chadwell）开发的程序XTRACT进行，基于下述计算假定：

（1）平截面假定，变形前、后均保持平面。

（2）忽略剪切变形影响。

（3）混凝土与钢筋充分粘结，无滑移。

（4）不考虑混凝土抗拉强度，混凝土受压本构如式（3）和图1（a）所示，钢筋均为三级钢（HRB400），设计强度fy＝360 N／mm2，本构关系如图1（b）所示。

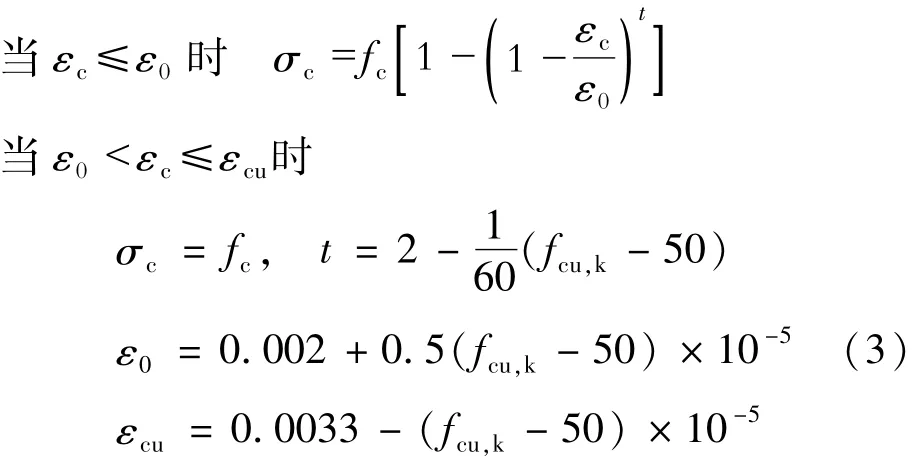
式中，fc为混凝土抗压强度设计值；σc，σs为混凝土和钢筋的应力；εc为混凝土压应变；ε0，εcu为混凝土峰值压应变和极限压应变；fcu，k为混凝土立方体抗压强度标准值；t为系数，且t≤2。

（5）纵筋极限拉应变取为0.01。

表1 EN 1992-1-1：2004中a取值Table 1 Value a for EN 1992-1-1：2004

a与轴压比n的二次函数关系如下式：

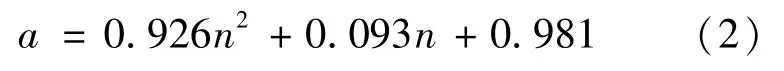
（6）纵筋沿截面周长均匀布置，计算时等效为沿截面四边厚度相等的钢筋膜，详见图2。

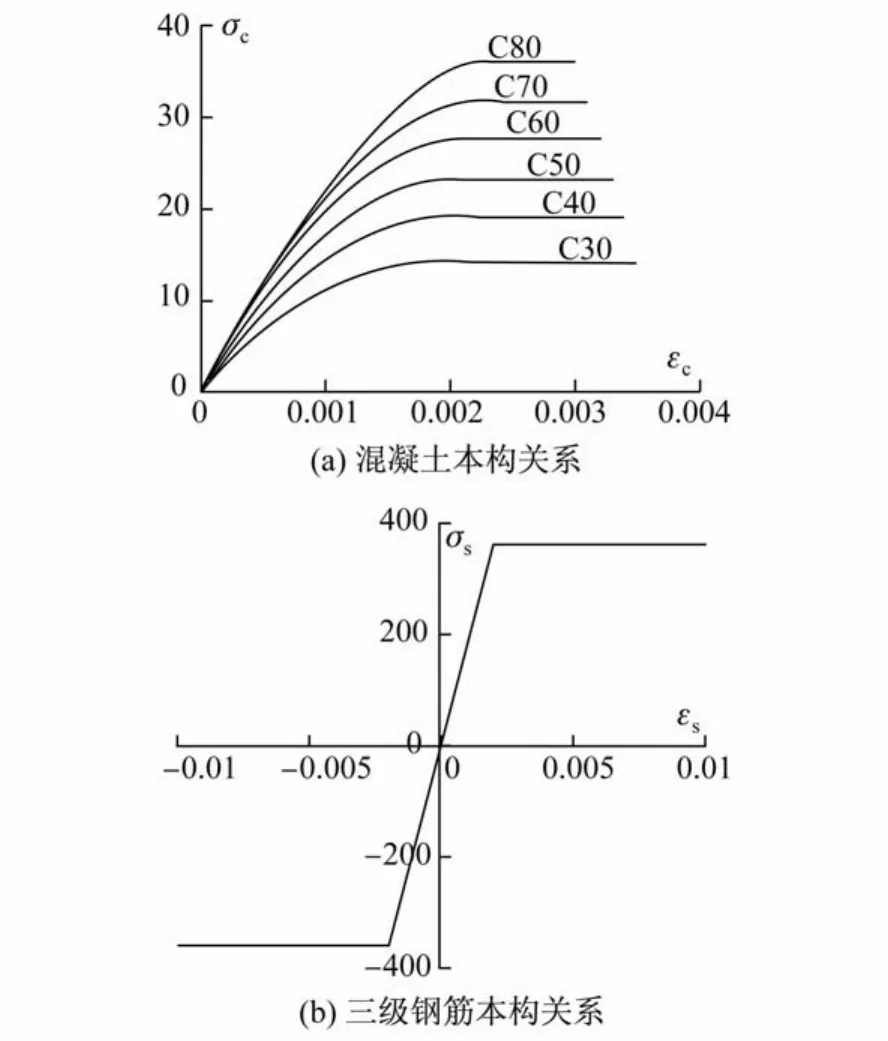
图1 混凝土、钢筋本构关系Fig.1 Constitutivemodels for concrete and steel

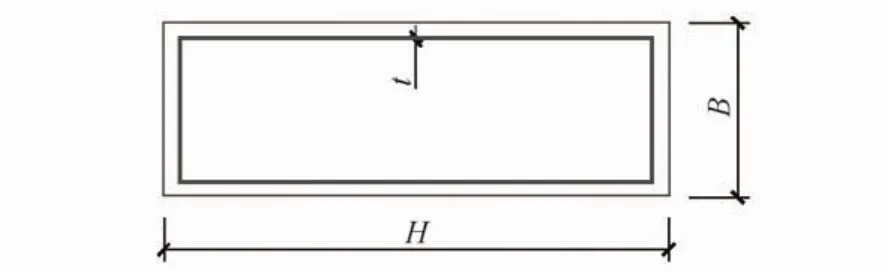
图2 均匀布筋等效钢筋膜Fig.2 Equivalent reinforced membrane

（7）保护层厚度均取25 mm。

2.2 截面承载力计算公式

将截面分为有限多个混凝土单元、纵筋单元，并近似取单元内应变和应力为均匀分布。为保持平截面，混凝土纤维和钢筋纤维的应变应满足以下公式：

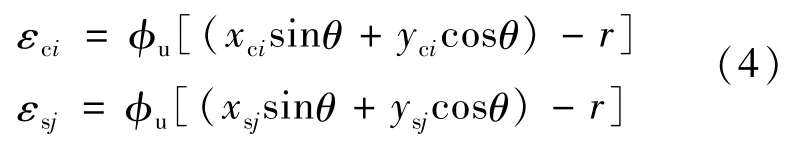
受压区外边缘混凝土压应变εc达到混凝土极限压应变εcu且钢筋纤维最大应变εs1＜0.01时，截面极限曲率φu应满足

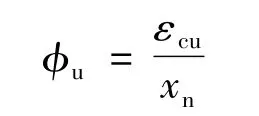
受压区外边缘混凝土压应变εc小于混凝土极限压应变εcu且钢筋纤维最大应变εs1达到0.01时，截面极限曲率φu应满足：

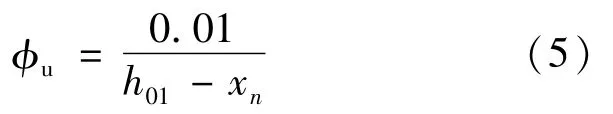
正截面承载力应满足：

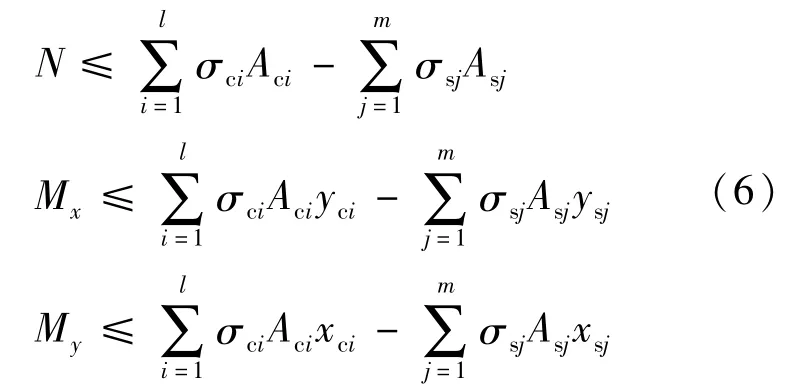
式（4）—式（6）中，N，Mx，My为设计轴力，绕x轴和y轴的设计弯矩；εci，σci，Aci为第i个混凝土单元的应变、应力和单元面积；εsj，σsj，Asj为第j个钢筋单元的应变、应力和单元面积；xci，yci为第i个混凝土单元中心到y轴和x轴的距离；xsj，ysj为第j个混凝土单元中心到y轴和x轴的距离；r为截面中心至中和轴的距离；h01为截面受压区外缘至最远钢筋纤维之间垂直于中和轴的距离；θ为x轴与中和轴的夹角；xn为中和轴至受压区混凝土最外侧边缘的距离。

3 无量纲强度面拟合及设计思路

3.1 设计强度控制面拟合思路

通过变参数多水平数值计算。首先，在布雷斯勒荷载等值线法基础上，确定定轴压比时归一化的无量纲弯矩等值线mx－my，找到其指数a与轴压比n的函数关系，重点考察高强混凝土和截面高宽比对等值线指数的影响；然后，回归沿截面主轴方向（x轴、y轴）轴压比n与无量纲化的弯矩˜m之间的函数关系。同时，引入无量纲参数λ，即纵筋配筋特征值，详见式（7），其实质是全截面钢筋强度与混凝土强度的比值。λ将截面纵筋配筋率、钢筋强度与混凝土强度联系起来，从而起到减少参数，提高结果曲线适用性的作用。mx，my，n与˜m定义见式（8）。

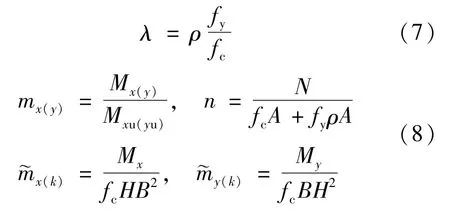
3.2 轴压比与荷载等值线的幂指数关系拟合

定轴力时荷载等值线关系式如下所示：

数值参数的选取范围见表2。根据《混凝土结构设计规范》（GB 50010—2010）中规定，全截面纵筋的最大配筋率不应大于5%，则对于强度为C30的混凝土，λ最大值为1.25，对C80的混凝土，λ最大值为0.50，为充分体现高强混凝土的曲线特征，表2中对0.01～0.05区间的λ取值进行了细分。计算结果详见图3。

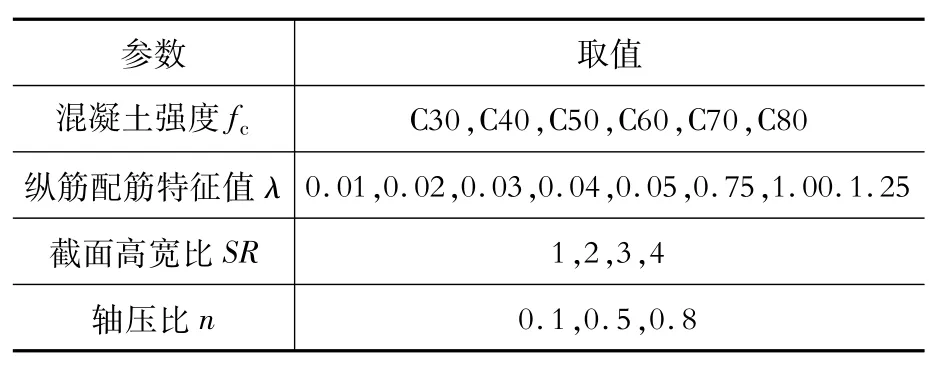
表2 模型参数及取值Table 2 M odel variables and the values

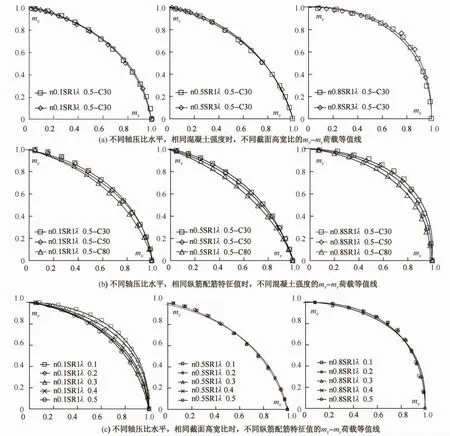
图3 mx－my荷载等值线Fig.3 mx－myload contours

由图3（a）可以看到，在其他影响因素相同时，高宽比不同截面的mx－my曲线几乎相同，说明经过无量纲化的荷载等值线不受截面高宽比影响。由图3（b）可以看到，在其他影响因素相同时，混凝土强度越高，mx－my曲线越向内收，即指数a越小，混凝土强度在C50以下时内收不明显，但在高强混凝土阶段（C60以上），内收幅度相对较大。由图3（c）可以看到，在其他影响因素相同时，纵筋配筋特征值越大，在大偏压阶段mx－my曲线越向内收，且相差较大，但当λ≥0.3时，曲线相差不明显。这与之前文献的结果类似，即大偏压阶段，指数a值由轴压比n决定，但受配筋率和混凝土强度影响；小偏压阶段则基本只与轴压比相关。根据上述曲线特征，相对保守地取λ＝0.5，SR＝1，混凝土为C50时计算得到的nmx－my曲面作为确定指数a的基础模型，忽略大偏压时纵筋和混凝土的影响。借助1stOpt（1.5版）软件对不同轴压比水平时的指数a进行最小二乘拟合，计算结果如图4所示，a－n的四次多项式回归关系如下式所示：

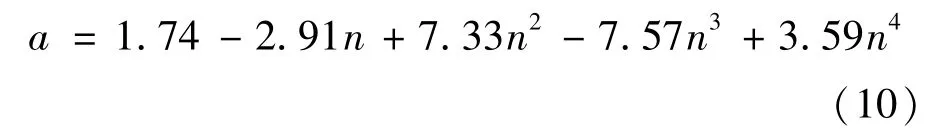
由图4可以看到：a－n曲线呈下凹形，参考计算结果，a的最小值在大小偏压界限点附近取得；在小偏压阶段与欧洲规范EN 1992-1-1：2004［5］相似；但在大偏压阶段，曲线相差较大；因美国规范ACI 318-05［4］中给出的是粗略的建议值，主要依据是布雷斯勒的建议值，在某些区段取值低于式10的拟合值。针对大偏压情况，经计算对比，曲线差异主要是布筋方式引起的，纵筋越靠近边中点，远离角点则a取值越小，但在本文研究的均匀布筋情况下，指数a的曲线应按图4呈下凹形。这种大偏压下的偏离现象在Shin［8］、Fossetti［1］及Bajaj［7］等的文献中也有出现。

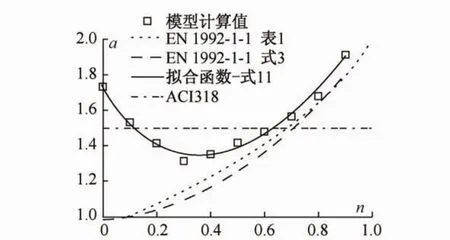
图4 a拟合曲线及对比结果Fig.4 a curve fitting and results comparison

3.3 无量纲相关曲线n－˜m拟合

经过两主轴方向的计算分析，当纵筋配筋特征值λ相同时，轴压比与归一化的无量纲弯矩（n－˜mk）曲线并不完全重合，如图5（a）所示，混凝土强度越大，曲线越向内收，图中曲线由外向内从C30过渡到C80，这与文献［9］中所得结论有差异。但按式（11）进行混凝土强度修正后，可以近似认为n－˜m曲线仅与λ相关。混凝土强度修正系数k1的取值见表3。

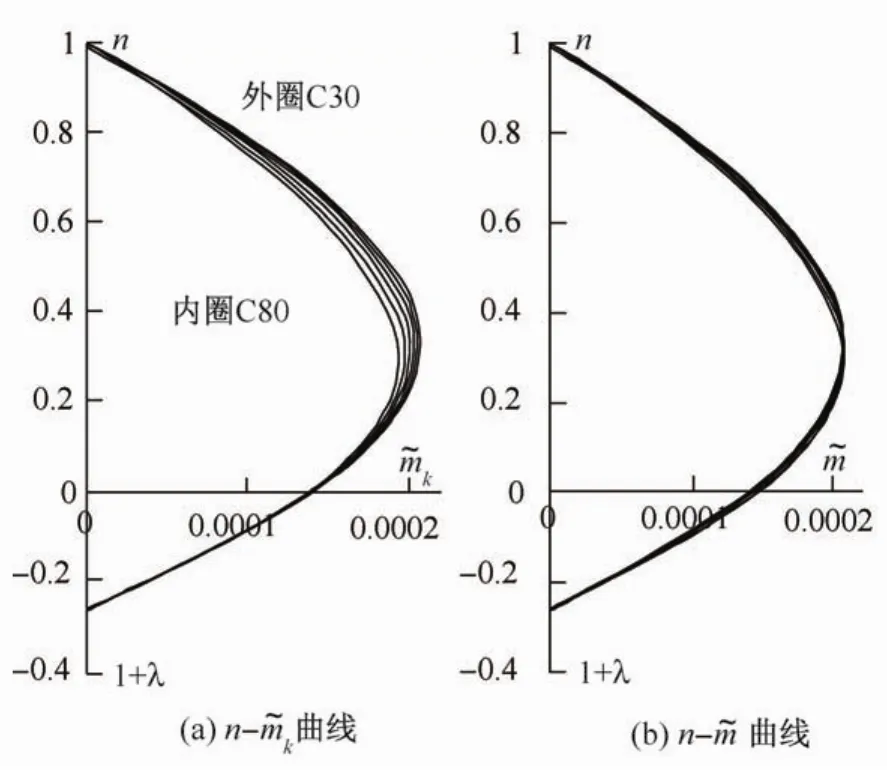
图5 n－˜m修正曲线Fig.5 n－˜m modified curves

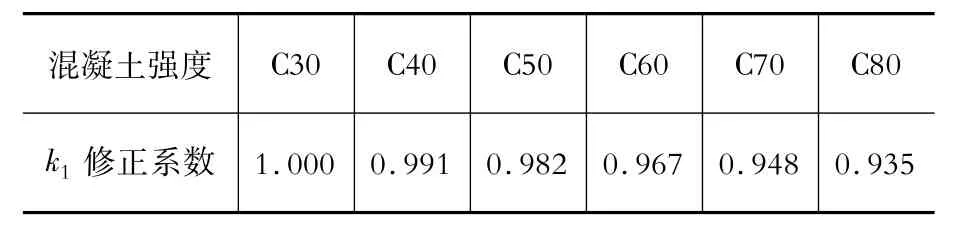
表3 修正系数k1Table 3 Adjusting factor k1

经混凝土强度修正后的n－˜m曲线如图6所示，实线为计算值，虚线为拟合值。n－˜m曲线中，相关弯矩最大值˜m0为截面高宽比SR及纵筋配筋特征值λ的函数，相对关系如图7所示，回归函数见式（12），k2为调整系数。

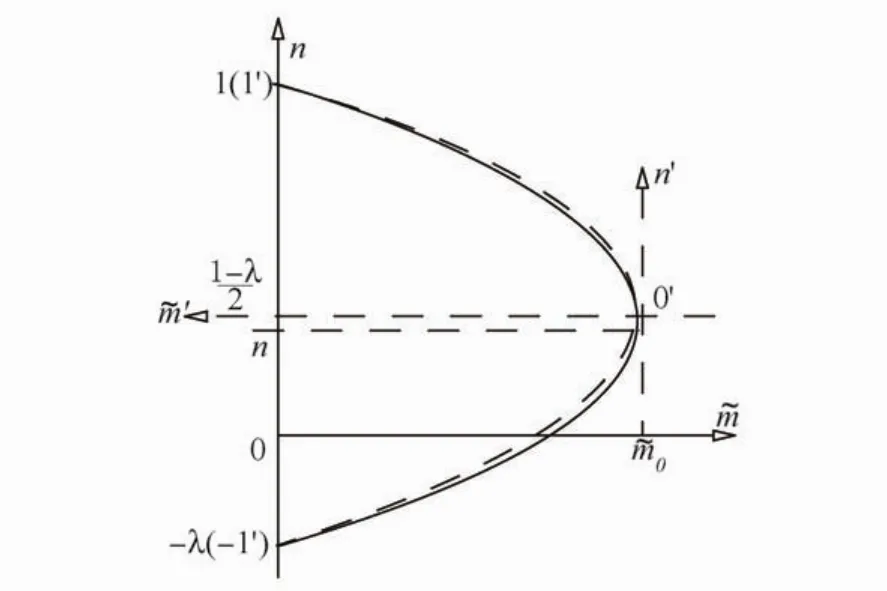
图6 n－˜m曲线的正规化处理Fig.6 Normalized n－˜m curves

图7 ˜m0－λ函数关系Fig.7 ˜m0－λfunctional relation

通过式（13）对图6中的计算值曲线（实线）进行正规化处理，即将原n－0－˜m坐标轴上的曲线向n′－0－˜m′坐标轴上转化，从而能以幂函数形式拟合原曲线（虚线）。假定拟合曲线关于n＝（1－λ）／2对称，大小偏压界限点位于对称轴上，这与实际结果有所不同，实际界限点对应轴压比为图6中的¯n，略低于对称轴。

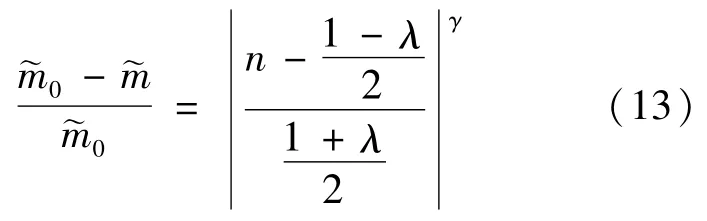
正规化处理后幂函数的指数γ与截面高宽比SR及纵筋配筋特征值λ的曲线关系如图8所示，图中圆点为拟合数据，回归函数见式（14），拟合函数均值0.997，方差0.01。

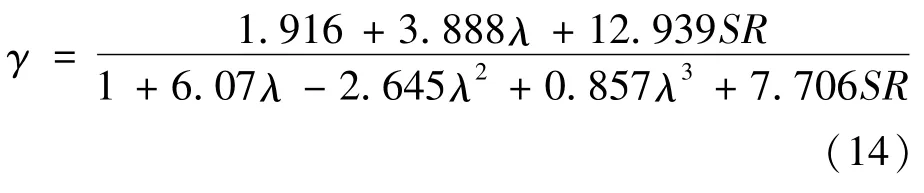
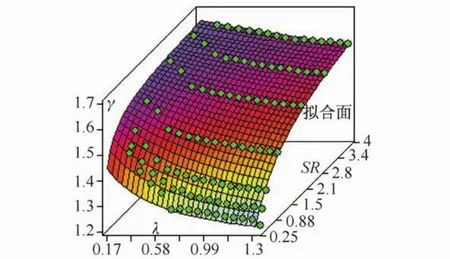
图8 γ－λ－SR函数关系及拟合曲面Fig.8 γ－λ－SR functional relation and the fitting surface

3.4 设计思路

基于上述强度面拟合结果，实际设计应用时可按图9的流程进行。这里纵筋配筋率的取值是关键，建议可取初值为0.05，并采用二分法逐步逼近精确值。考虑到按式（13）进行曲线归一化处理时对称轴的近似误差，出于安全考虑，定义

并在用于设计时限定f∈［0.90，0.95］，这样可以保证截面实际强度面包络设计强度面。

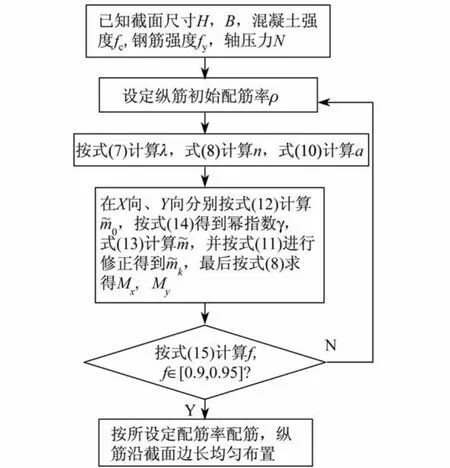
图9 设计流程图Fig.9 Design flow chart

4 拟合强度面准确性验证

为明确前述拟合强度面的准确性，采用文献［8，10］中的试验数据进行强度分析，并与试验结果进行对比，详细的分析结果见表4。以函数f评判破坏面的准确度，其数值越接近1则拟合度越好。从表4可以看到，除第一组试验中的试件RC-5和第二组中的MSC-B偏差略大外，拟合强度与两组双偏压柱试验结果吻合较好，这也说明按上述方法拟合双偏压柱强度面的做法可行，且基本满足精度要求。

5 算 例

矩形截面柱，截面尺寸为H＝600 mm，B＝300 mm，fc＝14.3 N／mm2，fy＝360 N／mm2，轴压力N＝1 500 kN，弯矩Mx＝120 kN·m，My＝220 kN·m，求按图10所示方式配筋情况下单根钢筋面积。

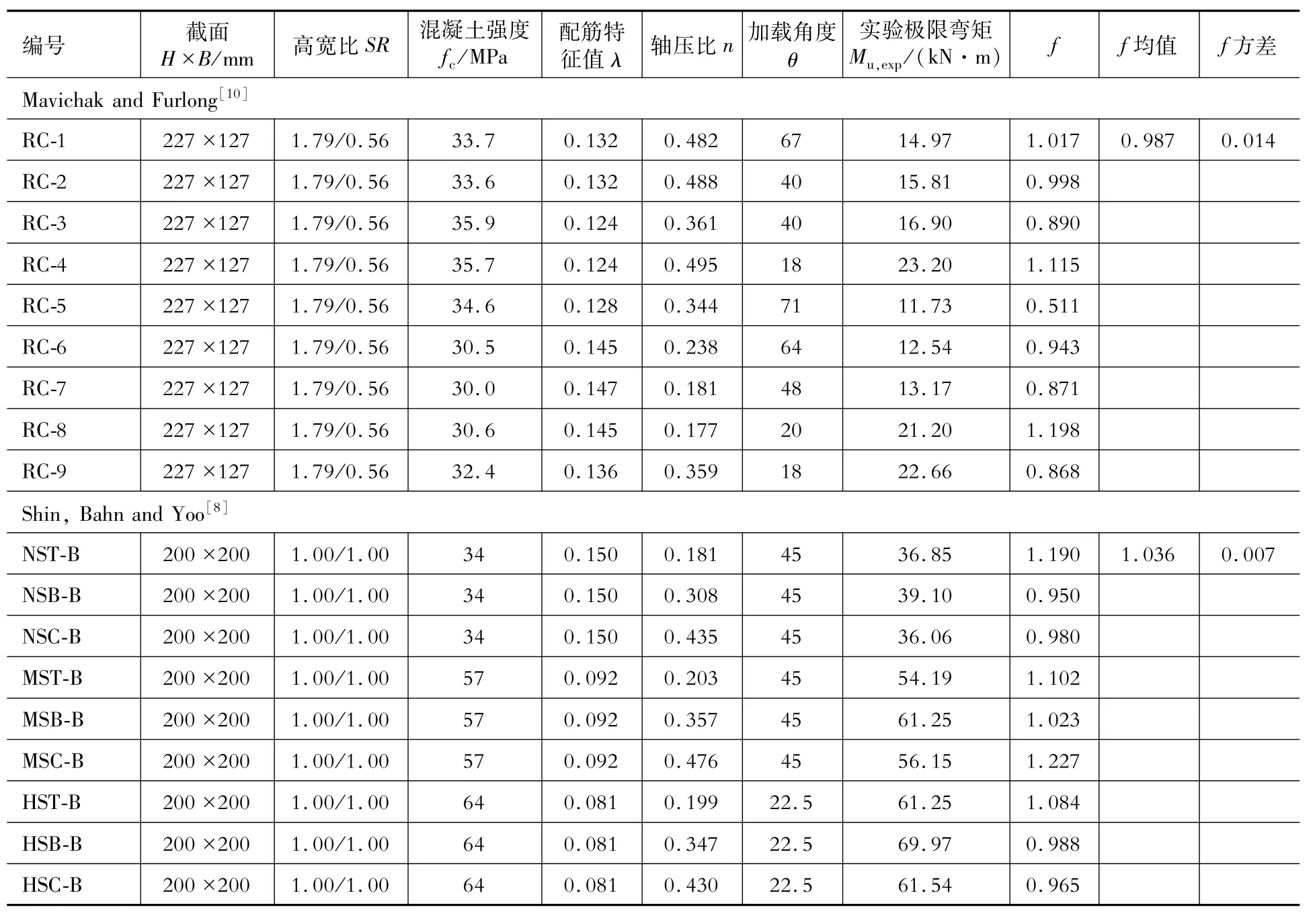
表4 试验值与计算值对比表Table 4 Com parison of calculated values and the test results

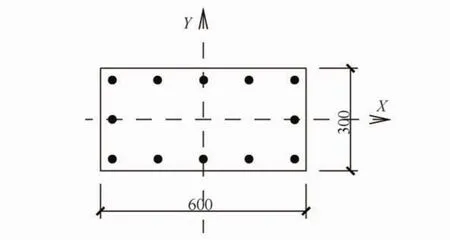
图10 均匀布筋示意图Fig.10 Uniformly distributed reinforcement

按图9所示流程，采用二分法选取纵筋配筋率，并进行迭代，详见表5。迭代到第4步就得到满足要求的配筋率，即ρ＝0.032。按此数值本例需配纵筋1225，实配筋率ρ＝0.033。

按上述计算配筋截面强度曲线与设计荷载之间的关系见图11，考虑到计算配筋值低于实配纵筋值，以及强度验算时出于安全考虑取0.9～0.95的折减（图9中的判别框），所得实际承载力曲线可以包络设计荷载。

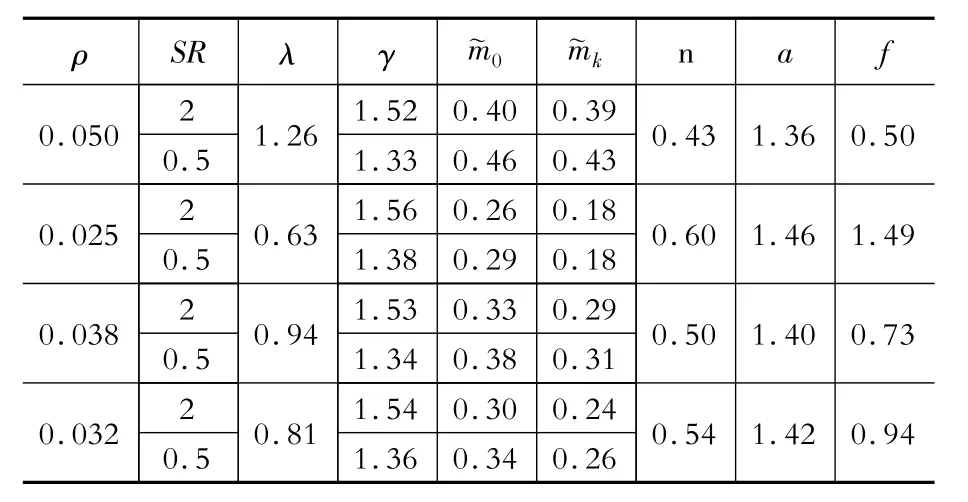
表5 变配筋率试算表Table 5 The trial of variable reinforcement ratios

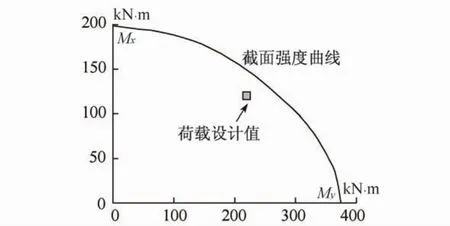
图11 截面强度曲线与设计荷载Fig.11 Section strength curve and design load

6 结 论

由前文所述可知，采用《混凝土结构设计规范》（GB 50010—2010）中规定的混凝土和钢筋的本构曲线，基于纵筋均匀分布的配筋方式以及荷载等值线理论，双偏压矩形柱的破坏面拟合曲线具有下列性质：

（1）归一化的极限弯矩曲线的相关指数与轴压比的函数关系a－n可用四次多项式拟合；

（2）两主轴方向正规化的轴压比与无量纲弯矩n－˜m的关系可用幂函数拟合；

（3）设计应用时，可根据拟合无量纲函数得到要求截面的强度面，再与设计荷载对比，通过有限次迭代可求解；

（4）拟合曲线可用于高强混凝土及大高宽比扁柱截面（高宽比≤4）；

（5）通过与试验结果的对比分析，所建议拟合曲线的精度能满足设计要求，有助于简化双偏压构件的设计过程。

［1］ Marinella F，Maurizio P.Dimensionless analysis of RC rectangular sections under axial load and biaxial bending［J］.Engineering Structures，2012，44：34-45.

［2］ Beal A N，Khalil N.Design of normal-and highstrength concrete columns.Proceedings of the Institution Civil Engineers［J］.Structure and Buildings，1999，134（4）：345-357.

［3］ Furlong RW，Hsu C T T，Mirza SA.Analysis and design of concrete columns for biaxial bending-overview［J］.ACI Structural Journal，2004，101（3）：413-423.

［4］ American Concrete Institute.ACI 318-05 Building code requirements for structural concrete［S］.2005.

［5］ Eurocode.EN 1992-1-1：2004 Design of concrete structures［S］.2004.

［6］ Parme A L，Nieves JM，Gouwens A.Capacity of reinforced rectangular columns subject to biaxial bending［J］.ACI Structural Journal，1966，63（9）：911-923.

［7］ Amarjit Singh Bajaj，Mendis P.New method to evaluate the Biaxial interaction exponent for RC columns［J］.Journal of Structural Engineering，2005，131：1926-1930.

［8］ Shin SW，Bahn B Y，Yoo SH.Effect of concrete strength on biaxial bending moment.Magazine of Concrete Research［J］.2006，58（2）：79-91.

［9］ 王丹，黄承逵，刘明，等.异形柱双偏压构件正截面承载力试验及设计方法研究［J］.建筑结构学报，2001，22（5）：37-41.Wang Dan，Huang Chengkui，Liu Ming，et al.Study of experiment and design method of normal section bearing for special-shaped column with double eccentric compression［J］.Journal of Building Strucures，2001，22（5）：37-41.（in Chinese）

［10］ Mavichak V，Furlong RW.Strength and stiffness of reinforced concrete columns under biaxial bending［R］.Research report7-2F.Center for Highway Research，The University of Texas at Austin，Texas，1976.

A Sim p lified Design M ethod for Uniform ly-reinforced Rectangular Columns Subjected to Axial and Biaxial Bending Forces

MA Zefeng1，2*LU Zhoudao1XU Jianli2CAIZihong2
（1.Research Institute of Structural Engineering and Disaster Reduction，Tongji University，Shanghai200092，China；2.Shanghai Institute of Architectural Design and Research，Shanghai200041，China）

Based on the load contourmethod，a series of section analysis of uniformly-reinforced rectangular RC columnswere performed under the guidance ofmulti-factor and multi-level orthogonal parameter strategy.The polynomial relation between the exponent value of the dimensionlessmoment contour and the axial load ratio was statistically fitted.By introducing the dimensionless quantity˜m in the principal axis direction，the variation relation ofmoment capacity over axial load ratio was decoupled.A simplified design method was proposed and also verified with existing experiment data.Finally，the design procedure was illustrated through an example.The proposed simplified method is of high precision and computational efficiency，and applicable to engineering design.

axial load and biaxial bending，load contourmethod dimensionless，related index

2013－11－05

*联系作者，Email：mazf＠siadr.com.cn