线缺陷光子晶体波导的透射特性研究

赵年顺，孙 剑

（黄山学院 信息工程学院，安徽 黄山 245041）

1 引 言

在过去十几年中，光子晶体[1-3]（PC）已经被证明在光电器件设计领域具有重要的应用价值，例如光波导、激光器、全光开关、滤波器、全光二极管，其中光波导器件[4-6]在全光传光中更是不可或缺。传统的光子晶体波导是通过在光子晶体中移去一些单元以形成导波通道。另一种新型的光子晶体波导是通过多个点缺陷的耦合形成的波导[7,8]，它的应用范围更广。它的物理机制是光能量被束缚在点缺陷中谐振并依次耦合通过各个点缺陷最终传播出去，这种线缺陷波导有着传统波导无法比拟的优点，如可以在原禁带中形成一个准平坦的杂质带，透射谱的范围比传统波导更宽。当引入克尔非线性时，该波导结构还可以被用来制作高效全光开关。[9-11]目前，在线缺陷方面的研究比较多，但研究方向多在光学器件的设计方面，并未对如何获得超平坦、宽频带的线缺波导进行分析。因此，分析影响线缺陷波导透射特性的一些因素将具有重要意义。

本研究采用二维光子晶体结构构建线缺陷波导，通过等间距地改变介质棒半径引入线缺陷，然后运用时域有限差分技术[12]（Finite Difference Time Domain,FDTD，美国R-soft公司研究开发的一种模拟实验软件技术）的软件对该类波导进行数值模拟计算并分析，计算中不断改变介质棒的层数，通过分析数据总结了线缺陷波导的透射谱随介质棒层数的变化规律。此外，改变点缺陷的半径，点缺陷缺陷模在禁带中的位置会发生变化，缺陷间的耦合程度不同，采用数值模拟法分析了点缺陷间的耦合特性，最终找到一种提高器件传播特性的方法。

2 物理模型

光子晶体结构的制备方法有很多，如使用飞秒激光干涉法、激光刻蚀技术等现代工艺均可实现。制作材料可选用传统介质如砷化镓（GaAs）或铝镓砷（AlGaAs）,基本结构如图 1所示。

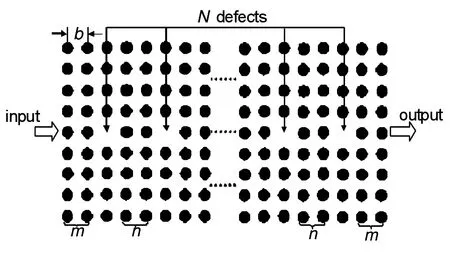
图1 二维光子晶体线缺陷结构

介质棒周期性分布于均匀介质空气（也可选则二氧化硅）中构成四方点阵结构，其中介质棒的折射率为n0=3.4，半径为R=0.2α，α=1μm指的是晶格常数。空气的折射率为n1=1。完整的光子晶体能阻止一定频率范围内的光通过，称为能量禁带。而通过改变介质棒的半径引入点缺陷，在缺陷处会形成一个量子化的束缚态，又称缺陷模。当原本处在能量禁带中的光能量与束缚态的能量一致时，便会发生谐振，使该禁带中的光能通过缺陷传播。当在完整光子晶体中引入一排点缺陷后，便会形成线缺陷通道，处在能量禁带中的电磁波便会依次耦合进点缺陷并最终传播出去。设点缺陷的半径为d，该波导有N个点缺陷，两相邻点缺陷之间介质棒的个数为n,波导两端介质棒的个数为m。改变n、m及r的数值并采用时域有限差分技术来模拟计算线缺陷波导的透射特性，在数值模拟中，选择格点尺寸为α/20，并设边界为完美匹配层。一般地，在光的传播过程中，电场能量被严格控制在缺陷中，光在光子晶体边缘的离散损失很少因此可以被忽略。

采用数值模拟方法计算得到完整光子晶体只存在TM模（磁场平行于介质棒）的能量禁带，第一禁带宽度为0.29-0.42c/a。在完整光子晶体结构中等间距的改变介质棒的半径形成点缺陷，原本处在能量禁带中的电磁波便会耦合进点缺陷并依次耦合到下一点缺陷最终传播出去，因此，所探测到的线缺陷透射谱处在第一禁带范围之内。这种光波传输通道称为线缺陷波导，又称为耦合腔波导（CCW）。

3 透射特性与结构参数的关系

在数值模拟中，首先选择点缺陷的个数N=10，缺陷半径d=0，缺陷间介质棒数n=4，调制波导两端介质棒的个数m并计算结果得线缺陷波导的透射谱如图2所示。

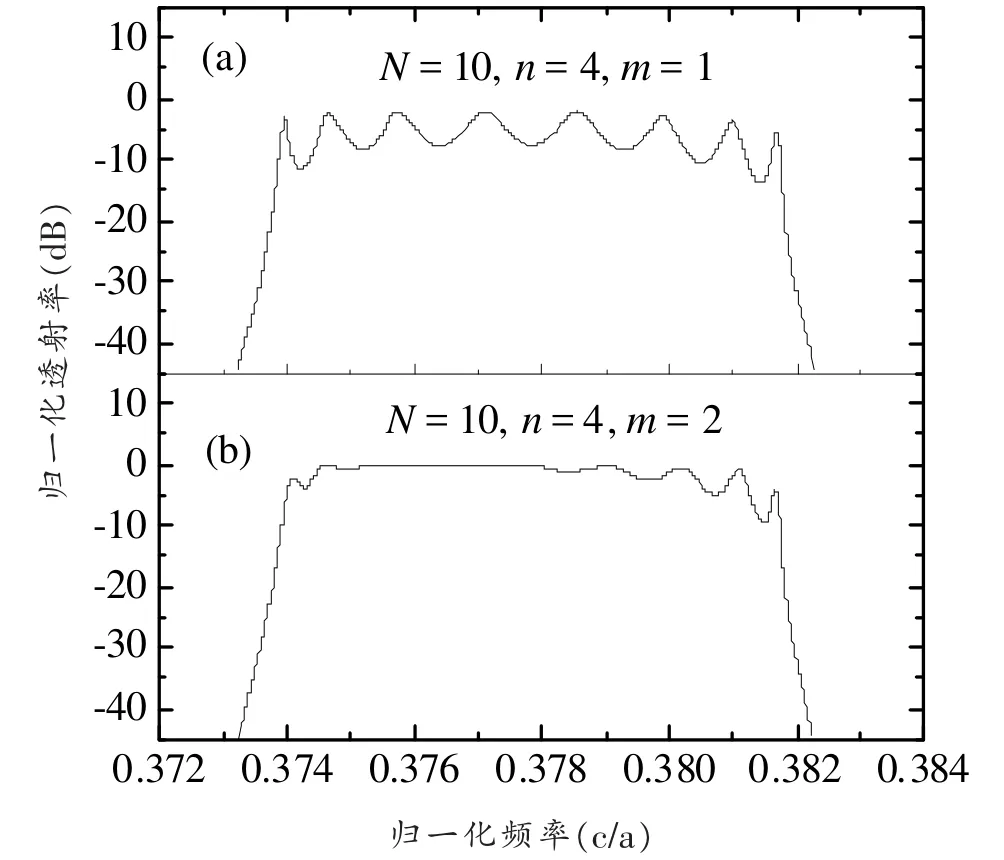
图2 n=4改变m的数值所得二维光子晶体线缺陷透射谱

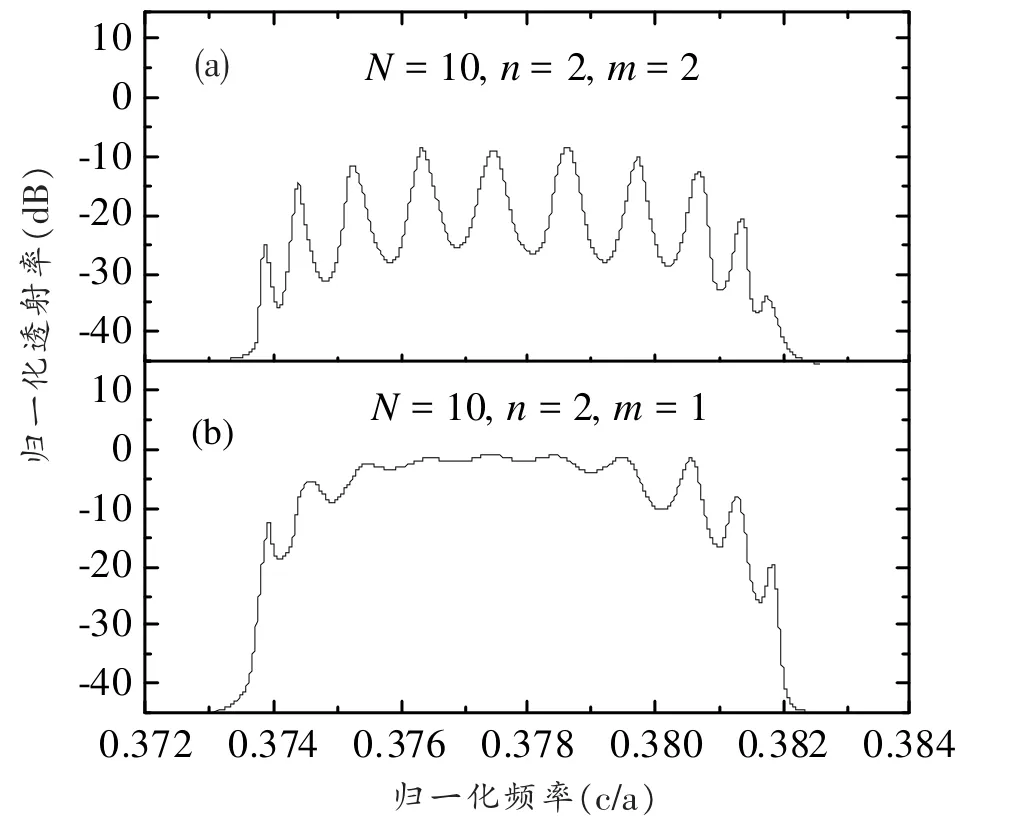
图3 n=2改变m的数值所得二维光子晶体线缺陷透射谱

对于完整的光子晶体，它的第一禁带在0.29-0.42c/a之间，当引入线缺陷时，会在原禁带处产生杂质带，频率在杂质带中的光可通过波导传播，由图2可知，m=1和m=2的两个线缺陷杂质带的幅度均在0.3732-0.3823c/a之间。在图2（a）中可以看到该结构透射谱分离出8个不同中心频率的振荡透射峰，振荡幅度可用对比度表示，约为7dB。与该现象不同的是，在图2（b）中呈现的是一个准平坦的透射峰，振荡幅度非常小。可以看出，该线缺陷波导的透射特性明显优于前者，也就是说m是影响透射特性的一个重要参数。

当改变两缺陷间相邻介质棒数为n=2，调制m的数值再来看透射谱会有怎样的变化。由FDTD法计算得到的透射谱如图3所示。从图中可以看到，对于m=1的线缺陷，它的透射谱波峰比较平坦，虽仍能看到存在有10个共振透射峰，但对比度非常小，而对于m=2的线缺陷，它的透射谱分离比较严重。

对比图2和图3不难发现，m和n都是影响透射特性的重要参数。改变m和n的值可以改变线缺陷波导的透射谱线，特别是当满足m=n/2的关系时，线缺陷波导便会出现一个低对比度、准平坦的杂质带。该结论为设计宽频带的线缺陷波导提供了参考。

4 缺陷半径对透射特性的影响

通过改变点缺陷的尺寸，缺陷模在禁带中的位置会发生移动。图4研究的是单个点缺陷的透射谱，图中分别给出了缺陷半径d=0.0a、d=0.3a、d=0.7a及d=0.9a的透射谱，半径为0.0a和0.7a的两缺陷中心频率在靠近禁带上边缘位置，半径0.3a的缺陷模在靠近禁带低频位置，另一个处在禁带中心位置。

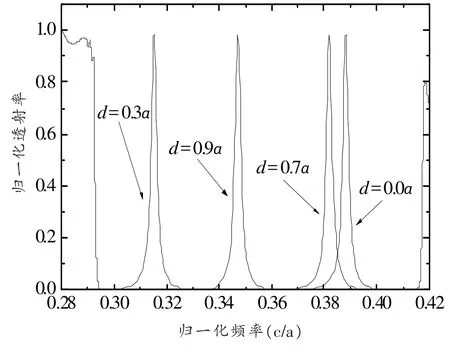
图4 不同缺陷尺寸的二维光子晶体点缺陷透射谱

为找到准平坦杂质带形成的物理机制，取不同的缺陷尺寸然后比较两个点缺陷耦合所得透射谱线的异同，图5是4个不同尺寸缺陷对耦合的透射谱线，由图中(a)和(c)所示，对于缺陷模在禁带高频一侧的点缺陷，两缺陷耦合后所得透射谱的线宽轻微变窄而波峰展宽且变得平坦。与之形成鲜明对比的是，缺陷模处在禁带低频一侧的点缺陷，如d=0.3a，耦合后形成明显的束缚与反束缚杂质带，透射谱也分离成两个独立的单峰形态，透射谱的线宽比单缺陷的线宽大得多。半径d=0.9a的点缺陷，处在禁带相对中间位置，耦合后存在两个振荡共振峰，但振荡幅度不高。所观察现象表明，准平坦的杂质带是由缺陷模处在禁带高频一侧的点缺陷耦合而成。

图5 不同缺陷尺寸的缺陷对耦合所得透射谱

为进一步说明点缺陷频谱与缺陷耦合波导频谱之间的关系，可将两者透射系数的关系表示为

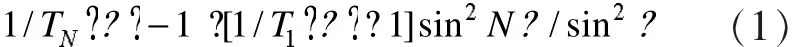
其中TN(ω)线缺陷的透射系数，T1(ω)表示点缺陷的透射系数，N指点缺陷的个数，β指一个周期结构的布洛赫相位。由公式可知，对于一个拥有N个点缺陷的波导，透射系数TN(ω)以π/N为周期，这就解释了线缺陷的杂质带拥有N个谐振峰的原因。而谐振峰的振荡幅度由1/T1(ω)-1决定，即要求透射系数T1(ω)较大，这时杂质带峰间才比较平坦，将得到比较好的透射谱。一般地，透射系数较大的透射谱，它的线宽则相对较窄。若由两个缺陷耦合所得的缺陷模线宽小于单个缺陷模的线宽，则由更多的点缺陷耦合成的波导也将拥有更窄的缺陷模线宽，所得杂质带透射谱线将更加平坦。例如图5中半径为0.0a的两个缺陷耦合所得频谱波峰平坦，线宽变窄，这就意味着这种缺陷耦合的线缺陷波导将拥有超平坦的杂质带。

5 总 结

采用数值模拟技术研究了线缺陷波导的透射特性，发现了影响透射特性的几个重要参数。首先，通过调制线缺陷波导的几何结构可以获得比较平坦的透射谱，这样的透射谱非常有利于信号的传输，此外也总结了调制结构参数的一些原则。其次分析了单个点缺陷的频谱与线缺陷波导透射行为的关系，并通过理论分析总结了这一规律。根据这些原则可以制作超平坦透射峰的线缺陷波导，而基于该波导的光学器件如延迟线、非线性全光开关，通道下载滤波器均能被实现。

[1]Yablonovith E.Inhibited spontaneous emission in solid state physics and electronics[J].Physical Review Letters,1987,58(20)：2059-2062.

[2]章亮，张巍，聂秋华,等.二维光子晶体波导研究进展[J].激光与光电子学进展，2013，50(3)：03008.

[3]曲连杰,杨跃德,黄永箴.光子晶体波导慢光特性研究[J].光学学报,2011,31(1)：180-185.

[4]Ho K M,Chan C T,Soukoulis C M.Existence of a photonic gap in periodic dielectric structures[J].Physical Review Letters,1990,65(10)：3152-3155.

[5]王济洲，熊玉卿，王多书,等．一维光子晶体缺陷模的滤波特性及应用研究[J]．光学学报，2009,29(10)：2915-2919.

[6]冯琛，冯国英，周昊,等.一维光子带隙光子晶体激光腔的特性分析[J].中国激光，2012，39(8)：0802009.

[7]魏琦,程营,刘晓峻.点缺陷阵列对声子晶体波导定向辐射性能的影响[J].物理学报,2011,60(12)：311-315.

[8]Scalora M,Dowling J P,Bowden C M,et al.the photonic band edge optical diode[J].Journal of Applied Physics,1994,76(10)：2023-2026.

[9]王荣,梁斌明,张礼朝.基于二维光子晶体点缺陷可调谐光功率分配器[J].光学学报，2012,32(1)：0123001-1-6.

[10]齐京仁.光子晶体带隙和缺陷的特性[J].光谱实验室，2012,29(5)：3235-3237.

[11]赵寰宇,何存富,吴斌,等.二维正方晶格多点缺陷声子晶体实验研究[J].物理学报,2013,62(13)：301-310.

[12]Noda S.,Chutinan A.,Imada M.Trapping and emission ofphotons by a single defectin a photonic bandgap structure[J].Nature,2000,407(6804)：608-610.