2-维Ablow itz-Ladik方程的调制不稳定性

王红县，张金良

（河南科技大学数学与统计学院，河南 洛阳 471023）

2-维Ablow itz-Ladik方程的调制不稳定性

王红县，张金良

（河南科技大学数学与统计学院，河南 洛阳 471023）

对2-维Ablowitz-Ladik方程的调制不稳定性进行了分析，导出了色散关系；通过理论分析和数值模拟，得到了调制不稳定性区域随耦合系数的增大而减小；对调制不稳定性区域内平面波的演化进行了模拟，验证了谱增益对平面波稳定性的影响。

2-维Ablowitz-Ladik方程；平面波；调制不稳定性；数值模拟

0 引言

由于孤立子在物理、生物、化学、通讯、交通规划等学科中有着广泛应用，所以有关孤立子的研究一直为国内外科学家们所关注。调制不稳定性（MI）与孤立子的形成密切相关，因为孤子被观测到的参数区域总是与调制不稳定性区域相同，因此调制不稳定性往往被认为是孤子形成的一个先兆。在调制不稳定性条件下，光脉冲在传播过程中往往会破裂成碎片［1］。

近年来，众多学者对调制不稳定性现象的研究做出了杰出的工作［2－4］。文献［5］利用离散多尺度方法，导出了Ablowitz-Ladik（AL）方程调制不稳定判据，数值模拟与理论分析结果是一致的；文献［6］对修正复Ablowitz-Ladik方程（MCAL）的线性稳定性做了理论分析，得到调制不稳定判据；文献［7］讨论了用来描述α螺旋蛋白质的摄动非可积Ablowitz-Ladik方程，分析了其平面波的调制不稳定性；文献［8］讨论了两组分三次－五次DNLS的调制不稳定性，研究了三次非线性项和五次非线性项对调制不稳定性的影响；文献［9－10］研究了Ablowitz-Ladik方程的调制不稳定性，导出了调制不稳定性判别条件，用数值模拟方法对理论分析进行了验证。以上主要是对一维方程的调制不稳定进行的研究，对于高维方程调制不稳定性分析的文献还很少见，因此，本文将对2-维离散Ablowitz-Ladik方程的调制不稳定性进行了研究，以期对二维波导中孤子的实验研究做出理论支撑。

本文首先导出2-维Ablowitz-Ladik方程的色散关系，分析耦合系数ε对调制不稳定性区域的影响；其次，利用数值方法，研究增益谱g（Ω）随平面波数d1和d2的变化情况；最后，对调制不稳定性的演化进行模拟，分析增益谱对平面波稳定性的影响。

1 耦合系数对调制不稳定性的影响

考虑2-维Ablowitz-Ladik（AL-NLS）方程：

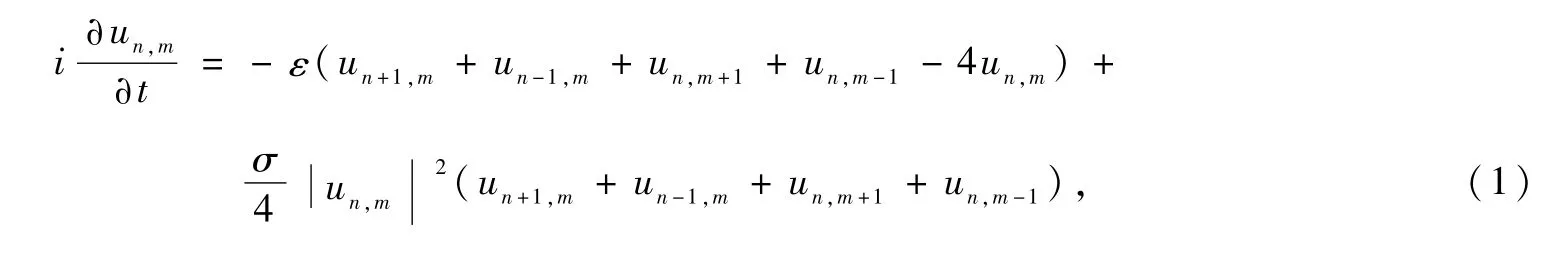
式中，un，m为二维格子空间中的复函数为耦合系数；σ＝±1（当σ＝1时，方程具有散焦效应，当

2 波数对调制不稳定性的影响

当Q1≠Q2时，利用数值模拟来探究波数d1、d2对平面波调制不稳定性的影响。

图1 M I的增益谱随平面波数的变化

取定σ＝－1，Q1、Q2、A的取值如图1，图2为ε变化时，M I的增益谱g（Ω）随平面波数d1和d2的变化。

图1和图2分别表示在散焦和聚焦情形下，对于不同的耦合系数ε，M I的增益谱g（Ω）随平面波数d1和d2的变化。

在聚焦情形下（σ＝－1），调制不稳定性的增益谱g（Ω）随平面波数d1和d2的变化。当ε＜1时，增益谱g（Ω）随着ε的增大而增大。当ε＞1时，增益谱g（Ω）随着ε的增大而减小，并且每个波峰逐渐演化为两个波峰。当ε＞10时，调制不稳定性区域与散焦情形相同。

图2 M I的增益谱随平面波数的变化

3 调制不稳定性演化的数值模拟

为了对2-维AL方程的调制不稳定性有直观的了解，利用四阶龙格－库塔法，对AL方程下所描述的运动进行了数值模拟。假设调制波的形式为：

其中，A ei（d1n＋d2m）为方程（1）的平面波精确解的初始形态；B为调制振幅；Q1和Q2为调制的波数。

图3表示图1a取定d1＝3，d2＝3时，un，m随时间t的演化。在演化过程中取定调制振幅B＝0.01。由图3可以看出：当t＝3时，平面波已出现调制不稳定性；当t＝10时，平面波显示较强的调制不稳定性。

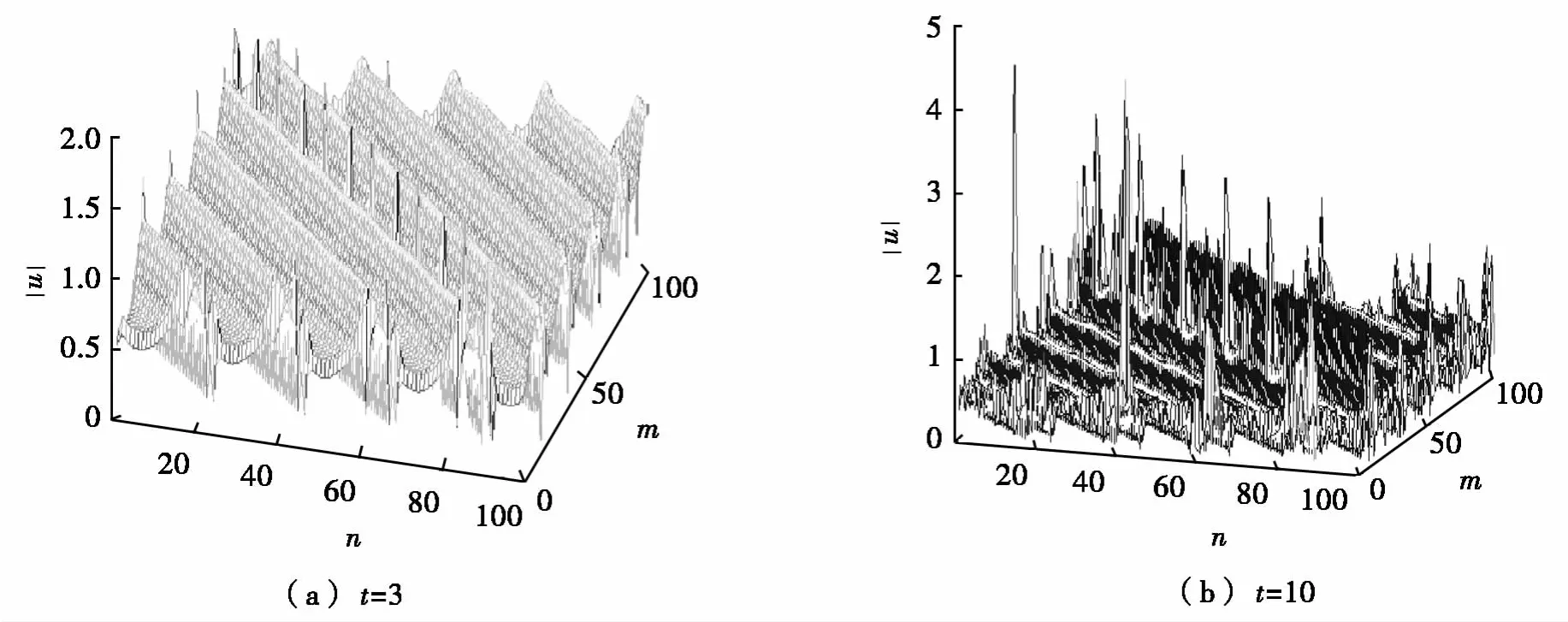
图3 un，m随时间t的演化

4 结论

当扰动波数Q1＝Q2时，在散焦情形下，当时，平面波具有调制不稳定性；当时，平面波不会出现调制不稳定性；在聚焦效应下，当时，平面波具有调制不稳定性，反之，平面波不会出现调制不稳定性。在散焦情形下，当cos d1cos d2＞0时，若有，平面波始终具有调制不稳定性；若有平面波不具有调制不稳定性。

在其他情形下，随着耦合系数ε的增大，平面波在波数d1和d2上调制不稳定区域逐渐缩小。

［1］ Dianov E M，Mamyshev P V，Prokhorov A M，et al.Generation of a Train of Fundamental Solitons at a High Repetition Rate in Optical Fibers［J］.Optics Letters，1989，14（18）：1008－1010.

［2］Alcaraz-Pelegrina J M，Rodríguez-García P.Modulational Instability in Two Cubic-quintic Ginzburg-Landau Equations Coup led with a Cross Phase Modulation Term［J］.Physics Letters A，2010，374（13）：1591－1599.

［3］ 钟先琼，向安平.高阶色散和指数饱和非线性光纤的调制不稳定性［J］.光学技术，2010（2）：274－278.

［4］ Chow K W，Wong K K Y，Lam K.Modulation Instabilities in a System of Four Coup led Nonlinear Schrodinger Equations［J］.Physics Letters A，2008，372（25）：4596－4600.

［5］ Mohamadou A，Fopa F，Kofane T C.Modulational Instability and Spatial Structures of the Ablowitz-Ladik Equation［J］. Optics Communications，2006，266：648－655.

［6］ Tabi C B，Mohamadou A，KofaneT C.Modulation Instability and Pattern Formation in Damped Molecular Systems［J］. Journal of Computional and Theoretical Nanoscinese，2009，6：583－592.

［7］ Ondoua R Y，Tabi C B，Fouda H P E，et al.Discrete Energy Transport in the Perturbed Ablowitz-Ladik Equation for Davydov Model ofα-helix Proteins［J］.The European Physical Journal B，2012，85：318.

［8］ Baizakov B B，Bouketir A，Messikh A，et al.Modulational Instability in Two-component Discrete Media with Cubic-quintic Nonlinearity［J］.Phys Rev E，2009，79：046605.

［9］ Mohamadou A，Tiofack C G L，KofanéT C.Stability Analysis of Plane Wave Solutions of the Generalized Ablowitz-Ladik System［J］.Physica Scripta，2006，74（6）：718.

［10］ Mohamadou A，Fopa F，KofanéT C.Modulational Instability and Spatial Structures of the Ablowitz-Ladik Equation［J］. Optics Communications，2006，266（2）：648－655.

O411.1；O175.7

A

1672－6871（2014）02－0086－05

河南省基础与前沿技术研究基金项目（092300410179，122102210427）；河南科技大学科研创新能力培育基金项目（2011CX011）；河南科技大学博士启动基金项目（09001204）

王红县（1989－），男，河南濮阳人，硕士生；张金良（1966－），男，河南唐河人，教授，博士，硕士生导师，研究方向为非线性数学物理问题.

2013－05－26