基于弹性悬链线理论的辊间输送带垂度特性的研究
庞晓旭,寇子明,李军霞
(1.太原理工大学机械工程学院,山西太原 030024;2.山西省矿山流体控制工程(实验室)技术研究中心,山西太原 030024)
基于弹性悬链线理论的辊间输送带垂度特性的研究
庞晓旭1,2,寇子明1,2,李军霞1,2
(1.太原理工大学机械工程学院,山西太原 030024;2.山西省矿山流体控制工程(实验室)技术研究中心,山西太原 030024)
针对输送机两托辊间垂度采用悬链线理论存在的不足,在分析现有辊间输送带垂度平衡方程的基础上,引入输送带弹性模量,建立了变形相容条件的辊间输送带弹性悬链线参数方程,导出了辊间最大垂度的解析解,并通过实例分析和仿真研究,验证了该参数方程及解析解的正确性。研究结果表明:辊间输送带最大垂度与弹性模量呈非线性倒数关系,与辊间距呈非线性平方关系,与输送带张力也呈非线性,张力越大,垂度越小,并进一步导出了基于弹性悬链线的相对垂度及相对垂度限制下的最小张力。
输送带;辊间垂度;弹性悬链线;弹性模量;有限元法
带式输送机的输送带垂度是影响输送机正常运行的重要参数,垂度过大会造成输送机运行阻力加大,增加输送机的运行成本,也不能达到节能减耗的目的[1]。目前国内对带式输送机垂度的计算主要参考《DTII(A)固定式带式输送机设计手册》,其规定输送带的相对垂度不得超过1%,计算公式为hr= qga cosδ/(8T)[2],对于输送机承载段和回程段,其q和a值不同。由上述公式可以看出,输送带的垂度没有考虑输送带弹性模量对其产生的影响,而输送带是黏弹性的连续体,当张力较大时必须考虑输送带的弹性变形,且上式成立的基础是托辊间输送带的长度要比两托辊间距大得多,而实际上输送带长度和两托辊间距基本一致,因此计算误差较大[3]。
本文在基于悬链线理论的基础上对水平运输两托辊之间输送带的垂度进行进一步研究,引入弹性模量,进而推导出更符合实际的弹性悬链线参数方程并进行仿真研究。
1 经典悬链线方程
缆索悬挂在两个架子之间时,当跨度足够大,对悬挂缆索受力分析时,悬挂的缆索可以看作是像链条一样柔软且无刚度的悬链,依此假设而进行的受力分析称之为“柔索理论”。17世纪伽利略首先研究了悬挂于两支架之间的缆索曲线线形,称之为“悬链线”[4]。该悬链线理论可以真实地反映悬索重力的特性。目前该理论已经广泛应用于悬索架桥等设计研究中。从上述分析可以看出悬链线理论的主要特征是跨度足够大、载荷均匀布置。其经典悬链线方程为余弦双曲线函数Y=αcosh X+γ[4],其中,a,γ为与自变量X无关的常量。
带式输送机是长距离的运输松散物料的设备[5],其钢丝绳芯输送带由橡胶和钢丝绳经硫化后组成[6],其具有黏弹性,在一定理想条件下符合悬链线的理论。依照悬链线的理论假设,则在对输送带的悬链线进行计算时,做如下假设:
(1)输送带是理想的弹性体,不受任何弯矩,只承受轴向张力[7];
(2)输送带张力符合胡克定律;
(3)作用在输送带上的载荷均指向统一方向,且沿输送带长度方向均匀分布;
(4)输送机为水平运输,无过大冲击等异常现象。
图1为输送带两托辊间的输送带受力情况。
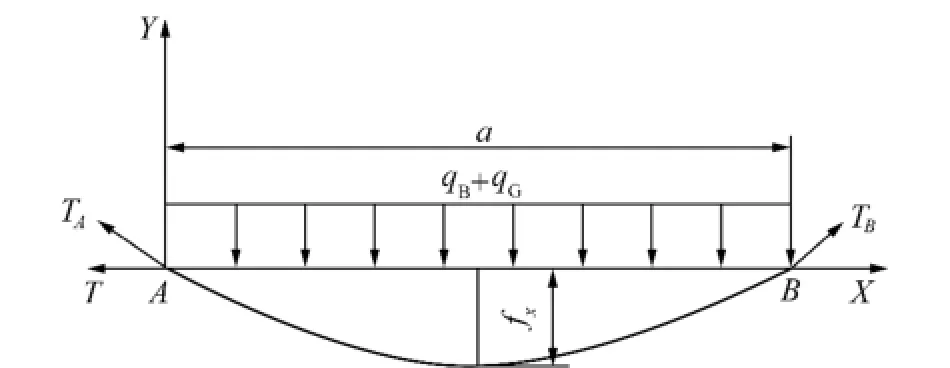
图1 输送带受力情况Fig.1 The force diagram of conveyor belt
以A点为坐标原点建立坐标系(图1),采用悬链线理论进行受力计算,则其悬链线方程为
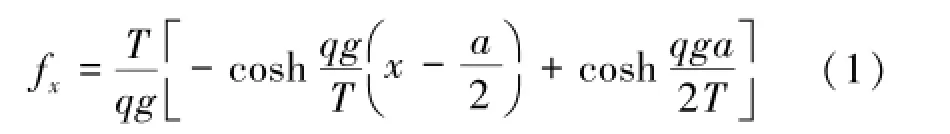
展开得

此结果与《DTII(A)带式输送机设计手册》中关于垂度的公式一致,由此可知采用悬链线进行垂度的计算是正确的。
2 弹性悬链线方程
由于输送带是连续黏弹性体,在输送机有较大的张紧力时不能忽略其弹性模量对输送机垂度的影响,基于此本文在经典悬链线的基础上推导两托辊间输送带的弹性悬链线方程。
假设输送带在变形前是水平的,设其轴线为X轴,A为坐标原点(图1)。选取输送带微元段d s研究(图2)。其力学平衡方程为

式中,T0为输送带张力,N;θ为输送带张力与X轴的夹角,(°)。
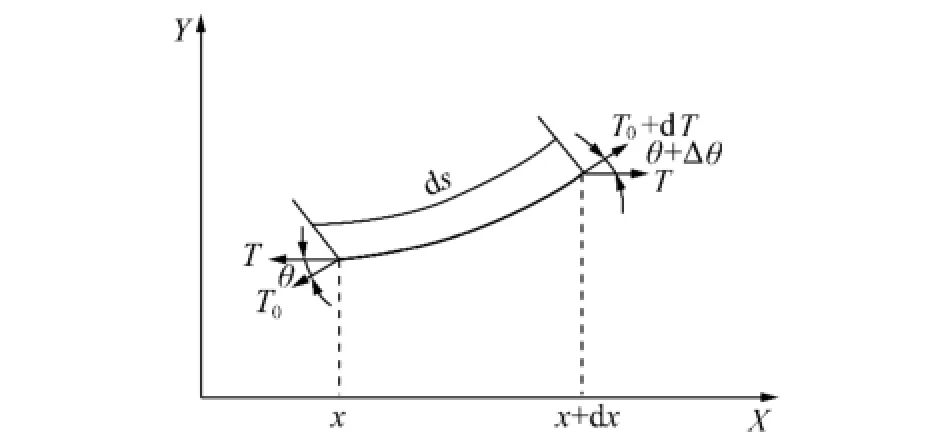
图2 输送带微弧段受力Fig.2 The force diagram ofmicro-arc of belt
由式(4)与式(3)相比可得

整理得
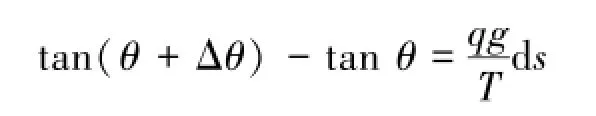
取极限求导得

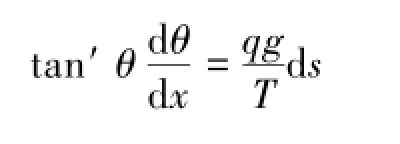
由胡克定律及质量守恒,输送带在受力变形前、后质量不变,则有
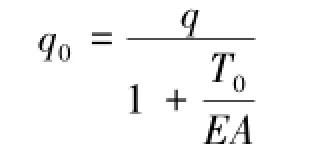
式中,A为输送带横截面面积;E为输送带弹性模量; q0为变形后的总质量。
由T0与T的几何关系,得T0=T 1+y′2,则微元段受力变形后的力平衡方程为

综上可得,两托辊间输送带的弹性悬链线参数方程为
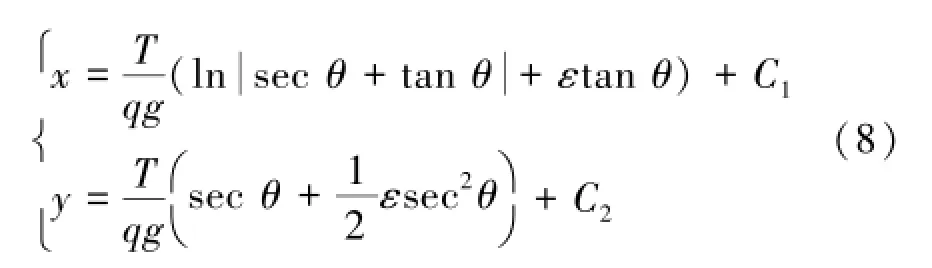
当不考虑ε或ε趋于0时,式(8)化简后即为经典悬链线。其ε的意义在于水平分量的张力与输送带宽度方向上的弹性力之比,即弹性变形。
当输送带位于在两托辊之间时,θ=θA和θ=θo分别为输送带张力与X轴夹角的最大值和最小值,则输送带的最大垂度为

由式(9)可以看出,弹性模量对输送带垂度影响很大,弹性模量越大,垂度越小,弹性模量与垂度呈非线性倒数关系。同经典悬链线一样,托辊间距越大垂度越大,张力越大垂度越小。
3 计算实例对比分析
以下是对某煤矿带式输送机输送带垂度的分析:
(1)带式输送机主要相关参数。

(2)采用经典悬链线方法求得的最大垂度。
(3)采用弹性悬链线方法求得的最大垂度。
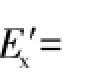
经换算选取E′=0.9 GPa为钢丝绳芯输送带ST1250的弹性模量,代入式(9),得输送带最大垂度为
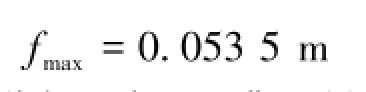
由以上计算分析可知:经典悬链线和弹性悬链线的计算结果存在很大偏差。因此引入弹性模量对输送带进行垂度分析是必须的。
4 仿真结果分析
4.1 仿真建立及仿真结果
对输送带进行ANSYS仿真[13],首先须对输送带材料属性进行定义,其定义的优劣直接决定了仿真的结果[14]。依据以上理论分析,取E′=0.9 GPa为钢丝绳芯输送带ST1250的仿真时弹性模量,泊松比取0.35,并用自由网格划分[15-16]。
对输送带X方向横截面施加UY=0的约束,对输送带整体施加UZ=0的约束。带式输送机输送带受到的力有输送带和物料的重力、运行阻力以及输送带的张力。对水平运输带式输送机输送带实际情况分析后,施加载荷与约束后如图3所示。
根据上述输送带实际参数进行仿真,其仿真结果如图4所示。由图4可知,输送带的最大垂度在两托辊中间点,其垂度为0.057 864 m,此与采用弹性悬链线方法的实例计算结果0.053 5 m基本一致,而与采用经典悬链线方法得到的0.013 4 m存在较大误差。

图3 输送带施加载荷及约束Fig.3 The applied load and constraint graph of conveyor

图4 输送带垂度仿真Fig.4 Sag displacement graph of conveyor belt
以上是针对某一实际参数对输送带的垂度进行分析。而从经典悬链线方程和弹性悬链线方程可以看出,托辊间距、输送带张力以及弹性模量E对托辊间垂度的影响较大。本文将分别对不同间距及不同张力下输送机垂度进行进一步分析,进而确认弹性悬链线方程的正确性。
4.2 辊间距的影响
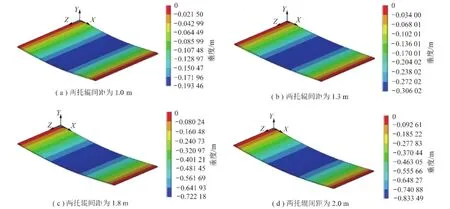
图5 a=1.0,1.3,1.8,2.0m输送带垂度仿真Fig.5 Sag displacement graph of conveyor belt at a=1.0,1.3,1.8,2.0 m
图5为张力为14 210 N时,两托辊间距分别为1.0,1.3,1.8,2.0 m下输送带弹性悬链线方程的垂度仿真。
4.3 张力的影响
图6为托辊间距为1.5 m,输送带张力分别为15 631,18 473,21 315,24 157,28 420 N时输送带弹性悬链线方程下的垂度仿真。
4.4 经典、弹性悬链线与仿真结果比较
(1)由图5可知,输送带垂度分别为0.193 46, 0.306 02,0.722 18,0.833 49 m。由此可见,输送机在张紧力一定条件下,随着托辊间距的增加,输送带最大垂度急剧增加,但是和托辊间距不呈线性平方关系,其总比平方计算结果大一定的数值。
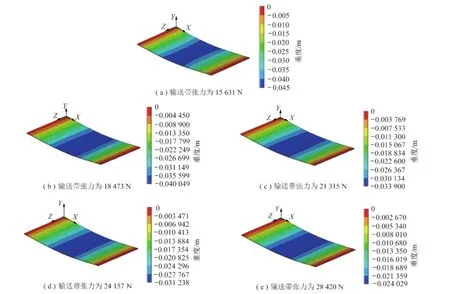
图6 T=15 631,18 473,21 315,24 157,28 420 N时输送带垂度仿真Fig.6 Sag displacement graph of conveyor belt at T=15 631,18 473,21 315,24 157,28 420 N
(2)由图6可知,输送带垂度分别为0.045, 0.040 049,0.033 900,0.031 238,0.024 029 m。输送机在托辊间距一定条件下,随着张力的增加,输送带最大垂度逐渐减小,和张力不呈线性倒数关系,其总比倒数计算值大一定的数值。
(3)由图5和6可知,托辊间距比输送带张力对输送带的垂度影响大,因此在进行输送带设计的时候,应该更注重托辊间距对输送带整体动态的影响。
(4)由图7可知,弹性悬链线的计算结果和仿真结果基本一致,而和经典悬链线的计算结果存在较大的偏差,因此本文所建立的基于弹性悬链线理论的辊间垂度方程是正确的,其更加符合实际工况。
4.5 相对垂度限定的最小张力
《ISO 5048—1989连续搬运设备带承载托辊的带式输送机运行功率和张力的计算》对辊间输送带的相对垂度hr标准[17]规定为

式(10)为两托辊间输送带垂度约束条件下的最小张力,即在托辊间距一定时用于确定黏弹性输送带的最小张力;当张力一定时,也可以确定托辊间距。
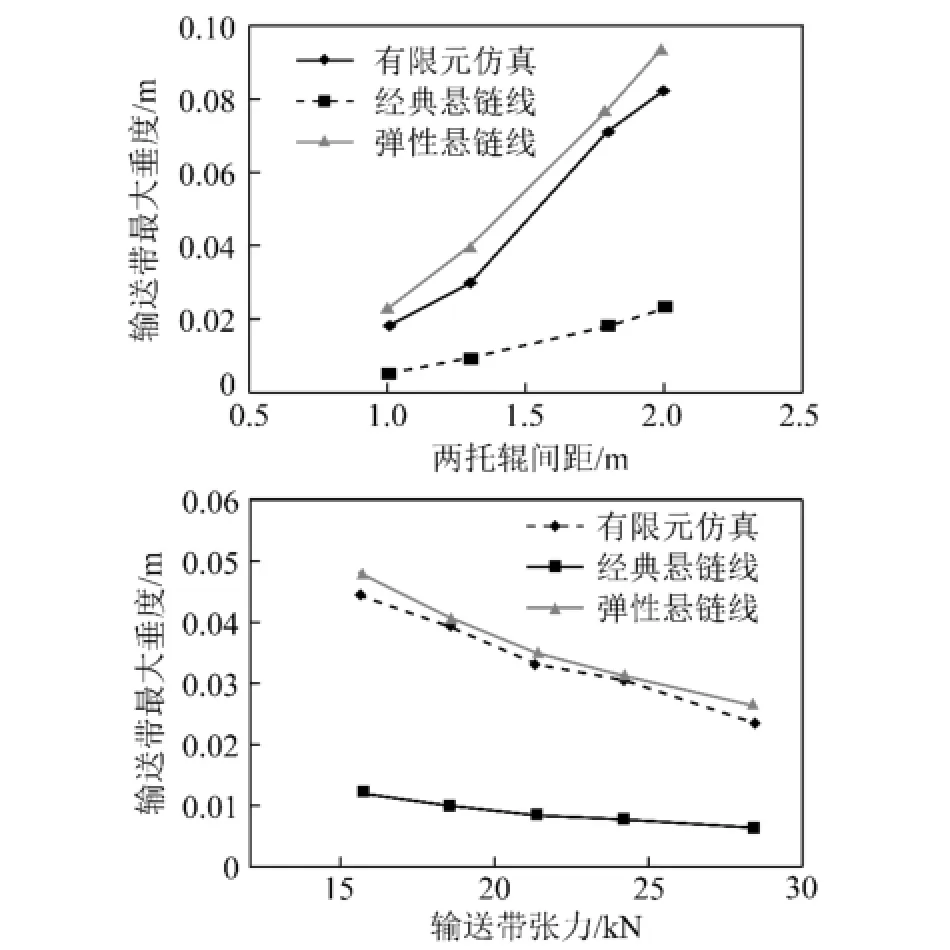
图7 输送带最大垂度计算值与仿真结果比较Fig.7 Comparison ofmaximum sag calculation ofconveyor beltwith the simulation results
5 结 论
(1)基于经典悬链线理论引入参变量弹性模量建立了变形相容条件的辊间输送带弹性悬链线参数方程,完善了输送带悬链线理论。
(2)通过建立局部坐标系的方法,得到了基于弹性悬链线方程的两托辊间输送带最大垂度的解析解,解决了两托辊间输送带最大垂度的精确算法问题。
(3)仿真和实例计算结果表明,采用弹性悬链线参数方程进行输送带的垂度计算结果和仿真结果基本一致,托辊间距对输送带垂度的影响比张力对垂度的影响更加重要,弹性模量与最大垂度呈非线性倒数关系,从而验证了弹性悬链线参数方程的可行性及正确性。
(4)根据相对垂度的要求,重新设定了相对垂度的表达式,并得到了垂度限制条件下的最小张力。
[1] 李光布.带式输送机动力学及设计[M].北京:机械工业出版社, 1998:29-33.
[2] 宋伟刚.通用带式输送机设计[M].北京:机械工业出版社, 2006:92-96.
[3] 陈树峰,蔡士兵.托辊间输送带大变形分析[J].煤矿机械,2004 (4):47-49.
Chen Shufeng,Cai Shibing.Accurate large deformation of the belt between the rollers[J].Coal Mine Machinery,2004(4):47-49.
[4] 郑丽凤.架空索道悬链线研究[D].福州:福建农林大学,2002.
Zheng Lifeng.Theory study of cableway on the catenary method [D].Fuzhou:Fujian Agriculture and Forestry University,2002.
[5] 朱立平,蒋卫良.适用于我国煤矿带式输送机典型机型的研究[J].煤炭学报,2010,35(11):1916-1920.
Zhu Liping,Jiang Weiliang.Study on typical belt conveyor in coalmine of China[J].Journal of China Coal Society,2010,35 (11):1916-1920.
[6] 输送设备制造商协会联合会.散装物料带式输送机[M].北京:机械工业出版社,1985:1-21.
[7] 丁 虎.轴向运动梁横向非线性振动建模、分析和仿真[D].上海:上海大学,2008.
Ding Hu.Transverse vibrations of axiallymoving viscoelastic beams: Modeling,analysis,and simulation[D].Shanghai:Shanghai University,2008.
[8] 宋伟刚,王 丹,左 博.单点驱动带式输送机动力学分析的半解析方法[J].煤炭学报,2012,36(1):217-223.
Song Weigang,Wang Dan,Zuo Bo.Semi-analytical solution to dynamic continuousmodel of belt conveyor with single drive[J].Journal of China Coal Society,2012,36(1):217-223.
[9] Mark Worth A J,Saunders JH.A model of structure optimization for a functionally graded material[J].Mater Lett,1955,22(17):103-107.
[10] 吴 波,廉自生,张 鑫.长距离带式输送机输送带的动态特性仿真[J].煤炭科学技术,2014,42(2):82-84.
Wu Bo,Lian Zisheng,Zhang Xin.Dynamic characteristic simulation for belt of long distance belt conveyor[J].Coal Science and Technology,2014,42(2):82-84.
[11] 李守新.功能梯度材料基础-制备及热机械行为[M].北京:国防工业出版社,2000:130-150.
[12] Clyne TW,Withers P J.An introduction tometalmatrix composites [M].London:Cambridge University Press,1992.
[13] 刘新华,王国法,刘成峰,等.两柱大采高液压支架的整架有限元分析[J].煤炭科学技术,2010,38(8):93-96.
Liu Xinhua,Wang Guofa,Liu Chengfeng,et al.Full set finite element analysis on two-leg high cutting hydraulic powered support [J].Coal Science and Technology,2010,38(8):93-96.
[14] 张元越.基于有限元的输送带模态分析[J].煤矿机械,2012 (2):91-92.
Zhang Yuanyue.Conveyor beltmodal analysis based on FEM[J].Coal Mine Machinery,2012(2):91-92.
[15] 周广林,张红华.基于ANSYS的苏制2×5×2.3型提升机支轮结构改造[J].煤炭学报,2008,33(1):99-102.
Zhou Guanglin,Zhang Honghua.Branch wheel structure reform of Russia-made2×5×2.3 hoistbased on ANSYS[J].Journalof China Coal Society,2008,33(1):99-102.
[16] 龚曙光.ANSYS工程应用实例解析[M].北京:机械工业出版社,2003:32-138.
[17] 宋伟刚.通用带式输送机设计[M].北京:机械工业出版社, 2006:91-92.
Research on the sag characteristics of inter-roll conveyor based on elastic catenary theory
PANG Xiao-xu1,2,KOU Zi-ming1,2,LIJun-xia1,2
(1.College ofMechanical Engineering,Taiyuan University ofTechnology,Taiyuan 030024,China;2.Mine Fluid Control Engineering Research Center(Laboratory)in Shanxi Province,Taiyuan 030024,China)
Aiming at the deficiencies in the catenary theory of the conveyor inter-roller sag,the elasticity modulus of conveyor beltwas introduced for establishing the elastic catenary parameter equation of the inter-roller conveyor belt in consistency condition and the analytical solution to themaximum inter-roller sag was derived based on the analysis of the current inter-roller sag equilibrium equation,and whose correctness was verified by the case analysis and simulation research.According to the research result,themaximum inter-roller sag of the conveyor belt is in non-linear reciprocal relation with its elasticmodulus,in nonlinear quadratic relation with inter-roller gap,and also in nonlinear relation with conveyor belt tension while the greater the tension is,the smaller the sag will be.Meanwhile,theminimum tension under the relative sag and its restriction was further developed on the basis of elastic catenary.
belt conveyor;rolls sag;elastic catenary;elastic modulus;finite elementmethod
TD528
A
0253-9993(2014)07-1379-06
庞晓旭,寇子明,李军霞.基于弹性悬链线理论的辊间输送带垂度特性的研究[J].煤炭学报,2014,39(7):1379-1384.
10.13225/j.cnki.jccs.2014.0065
Pang Xiaoxu,Kou Ziming,Li Junxia.Research on the sag characteristics of inter-roll conveyor based on elastic catenary theory[J].Journal of China Coal Society,2014,39(7):1379-1384.doi:10.13225/j.cnki.jccs.2014.0065
2014-01-16 责任编辑:张晓宁
国家自然科学青年基金资助项目(51105265);新世纪优秀人才支持计划资助项目(NCET-12-1038);山西省高等学校优秀青年学术带头人资助项目
庞晓旭(1983—),男,河南叶县人,博士研究生。E-mail:pxx8308@163.com
——垂度法

