基于信息融合的隔爆开关永磁机构储能电容失效诊断

刘晓明,牟龙华,张 鑫

(同济大学电气工程系,上海 201804)

基于信息融合的隔爆开关永磁机构储能电容失效诊断

刘晓明,牟龙华,张 鑫

(同济大学电气工程系,上海 201804)

针对利用单一判据对隔爆开关永磁机构储能电容进行故障诊断时存在较高的误判率的问题,提出了一种基于信息融合理论的电容失效诊断方法。通过分析储能电容的失效机理,得到其有效的故障特征参数,从而建立了储能电容状态评价的证据体系;为避免经验赋值的主观性,提出了基于模糊熵的最小模糊度优化模型,以此模型求取储能电容诊断模糊系统隶属度函数中的未知参数,并构建基于隶属度的电容状态基本概率分配函数。利用D-S证据合成规则实现多种故障信息的融合,并根据基本概率分配(BPA)决策准则来判断储能电容的状态。根据现场采集的数据,利用这种方法进行了实例分析,得到了其储能电容的当前状态评估结果,分析结果验证了该方法的有效性。

储能电容;失效诊断;D-S证据理论;模糊隶属度;模糊熵

矿用高压隔爆开关是煤矿井下供电系统中的关键设备,其工作性能直接影响着煤矿井下的供电质量与安全生产。真空断路器是高压隔爆开关的关键部件,其操作机构的优劣对断路器的分合闸动态性能起着极为重要的作用。相比传统的弹簧操作机构,利用永磁保持、电子控制的永磁操作机构具有不可比拟的优点,因此近年来成为隔爆开关真空断路器广泛应用的驱动元件。

永磁操作机构本体可靠性较高,机械寿命可达104次,但其控制器尚存电源系统不可靠、电磁干扰等不足,是井下应用中尚未解决的重要问题[1-2]。应用情况表明,永磁机构控制器的电源系统(储能电容器)的运行状态及评估是用户最为关心的方面。若能充分利用好永磁机构的优势又将用户关心的问题解决好,这必将使永磁机构隔爆开关得到更广泛的应用。因此,文献[3]设计了一种具有电容器特性在线监测的控制电路,通过比较永磁机构储能电容的充电时间来实现电容器的状态诊断。然而,故障模式及其特征间有着复杂的对应关系,以及故障诊断过程中存在各种不确定因素的影响,因此,这种单证据诊断方法的精度和可靠性已显不足。

本文对永磁机构储能电容故障特征参数(等效串联电阻(ESR)、电容量(C)、充电时间(t))进行了分析,提出一种将模糊理论与D-S证据理论相结合的故障诊断方法。通常,利用D-S证据理论进行故障信息融合的关键问题是基本概率分配函数(basic probability assignment,BPA)的构建,对此,本文建立了基于模糊熵的最小模糊度优化模型,通过该模型优化可得到隶属度函数的未知参数,进而提出基于模糊隶属度的BPA构建方法,这样避免了经验性赋值的主观性,提高了故障诊断的可信度。最后根据BPA决策规则,并结合实例数据,得到永磁机构储能电容的状态评估结果。

1 故障特征参数分析

储能电容作为永磁机构控制器的电源系统,由交流电源经整流后为其充电。当合(分)闸信号来到时,向合(分)闸线圈瞬时放电,产生很高的脉冲电能,从而使断路器顺利合(分)闸[4-5]。电容储能的多少直接影响合(分)闸线圈中电流的大小,因此它必然对合(分)闸时间产生影响。电容储存的电能应足以进行分—合—分操作,且要求在每次放电后能再次充满。目前,电解电容器由于其成本低、容量大,被广泛用作永磁机构的储能部件。

工作条件下,电解电容的电极发生着缓慢的原电池反应。随着阳极金属氧化膜的不断修复,产生不平整的表面,导致电介质的介电性能及耐压性能降低;增厚的电介质还会引起C,ESR增大;阴极反应产生的氢气会加速电解液的蒸发[6]。同时,作为永磁机构储能装置的电解电容,其充放电过程中变化的电压在通过电介质时会引起能量损耗,再加上漏电流造成的能量损耗,都会导致电容内部温度升高,高温运行会进而加速电解液的散失。随着内部电解液的减少, ESR将增大,C将减小[7-9];ESR的增大将增加电解电容的功率损耗,进而升高电容器的内部温度,加速电容性能的退化。

因此,长期的过电压、高温运行会造成电容电介质的散失,从而引起储能电容的劣化直至失效,这是永磁机构的显著缺陷。

国内外学者通过实验测量分析,得到储能电容基于ESR的寿命标准,即当ESR超过初始值的3～4倍时,电解电容失效。同时,文献[10]表明,当电解电容的C减小20%时也会导致电容失效。因此,除了文献[3]给出的t外,ESR和C都可以作为表征储能电容失效的故障特征参数。

以上故障特征参数值的变化与储能电容内部物理、化学反应密切相关,且均无法直接测量,都需要选择适当的监测信号经计算后间接得到,因此,在不同特征参数所对应的判据下,诊断结果往往存在冲突与矛盾。D-S证据理论作为一种不确定性的推理方法,能有效的解决这种证据冲突和不确定性,通过融合多方面的故障信息以实现对设备的准确诊断[11]。

2 基于信息融合的失效诊断

2.1 基本理论

定义1 对于一个判决问题,其所有可能答案的完备集合用Θ来表示,且Θ中的所有元素两两互斥,则称Θ为辨识框架。

定义2 设Θ为辨识框架,且Θ包含p个子集, Ai表示辨识框架Θ的子集,若有函数m是2Θ→[0, 1]的映射,且m满足：

(1)对于空集Ф,有m(Ф)=0;

(2)对于任意Ai∈2Θ,∑m(Ai)=1。

则称m(Ai)为事件Ai的基本概率分配函数,表示证据支持命题Ai的程度,如果m(Ai)＞0,则Ai称为证据焦元。

定义3 设m1,m2为同一识别框架上的两个证据体的基本概率分配函数,其证据焦元分别为X1, X2,…,Xp和Y1,Y2,…,Yq,则D-S合成法则定义了证据融合后的基本概率分配[12]为

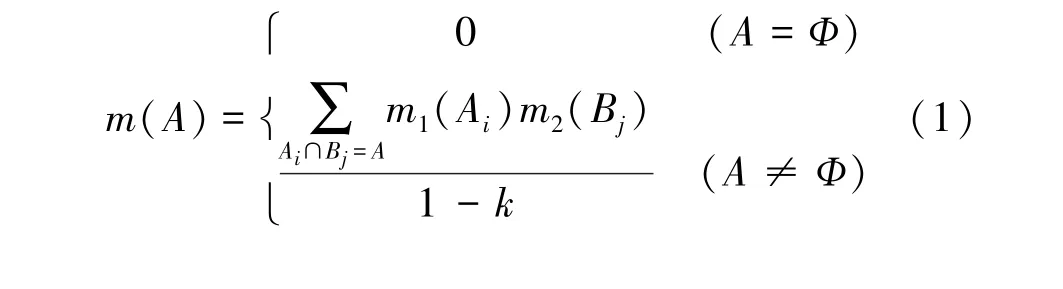
作为一种信息融合技术,D-S证据理论就是在同一识别框架下,用不同的方法对同一问题单独进行相应的处理,每种处理结果称为单一证据体;通过合成规则将来自2个以上的单一证据体的基本概率分配融合为一个新的基本概率分配,并以融合后的概率分配作为决策依据[13-14]。

2.2 故障信息融合模型

选取ESR,C和t这3项指标来描述永磁机构储能电容的运行状态。设m1,m2,m3分别为ESR,C,t的基本概率分配函数;A1,A2,A3,A4分别代表储能电容器良好、一般、预警和失效4个状态,它们构成辨识框架Θ。

2.3 基于模糊隶属度的基本概率分配

多信息融合的关键是如何根据现有的数据构造出基本概率分配函数[14]。基本概率分配函数的值不是概率,而是根据设备检测所得的数据构造出来,或根据专家经验给出。由于模糊数学中隶属度函数能够表征研究对象某项指标属于某种或者具有某种特性的程度,是描述差异的中间过渡与不确定性的有效理论[15],因此,文中利用模糊隶属度来确定各证据指标的基本概率分配。

隶属度函数的确定目前还没有一套成熟有效的方法,大多数还依靠经验与实验,常见的隶属度函数有三角形、梯(半梯)形、高斯和S型等,隶属度取值范围通常为0～1,其中模糊度最大的位置为0．5[16-17]。本文选择最常用的三角形和梯形隶属度函数来构造基本概率分配,如图1所示。

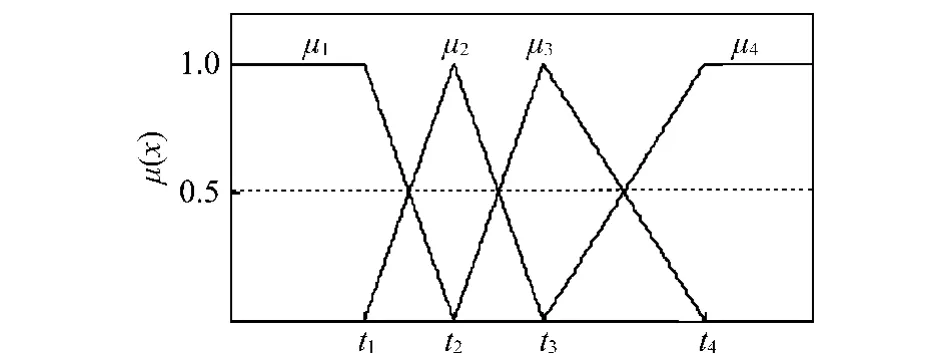
图1 半梯形和三角形隶属度函数Fig．1 Membership function diagram of half trapezium and triangle

理想的隶属度函数应该在反映模糊概念的模糊特性的同时,又尽可能清晰地描述出证据指标所表达的客观内容,然而,建立这样一个恰如其分的隶属度函数不是件容易的事。从模糊集的模糊性度量角度可知,只要是不恒为1或0的隶属函数均可反映出模糊性,而反映事物客观性的清晰程度则可用模糊集的模糊度来度量,模糊度越小的模糊集,其表达问题本质的准确性就越大。因此,利用最小化模糊度的原则计算隶属度函数的相关参数,能够使其表述得更为客观准确。

2.3.1 基于模糊熵的隶属度函数优化模型

“熵”的概念最早起源于物理学,用于度量一个热力学系统的无序程度。信息论把它作为随机变量不确定性程度的一种度量,而在模糊理论里,熵被用来测量模糊集或模糊系统信息的模糊程度。模糊熵与信息熵有很大的区别,前者是基于隶属度函数,用来描述一种模糊不确定性,后者则是基于概率函数,用来描述一种随机不确定性[18]。因此,文中选择模糊熵作为模糊度的度量方式,熵值越大,模糊集的模糊度越大,熵值越小,模糊集的模糊度就越小。

假设一模糊集X={x1,x2,…,xN}的隶属度函数为μ(x),则其模糊熵的表达式为

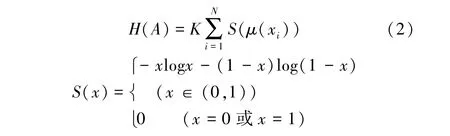
式(2)中,通常取常数K为1/N,取log函数的底为2,则经整理得

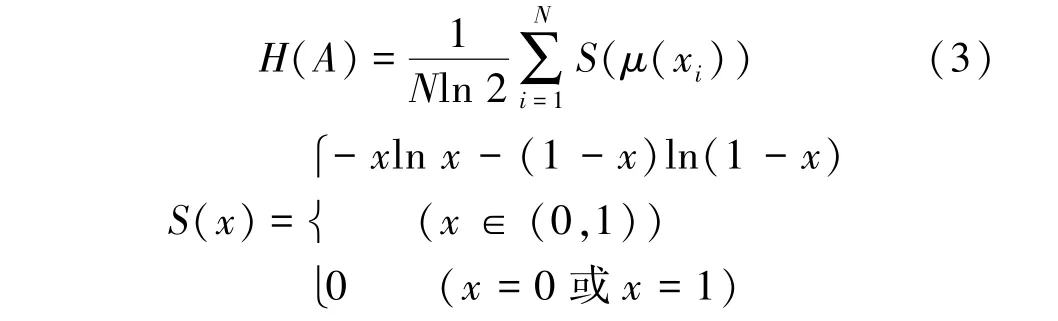
对于本文储能电容状态诊断的模糊系统M= {A1,A2,A3,A4},设其对应的隶属度函数为μ1,μ2,μ3, μ4,如图1所示。根据最小模糊度原则,在模糊熵表达式(3)的基础上建立如下隶属度参数优化模型：

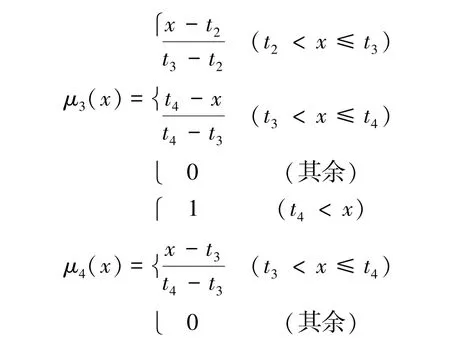
式中,N表示模糊系统中所有样本的个数;Nj表示论域Aj中的样本个数;xi表示模糊系统中第i个样本; xij表示论域Aj中的第i个样本。

与模糊熵的表达式(3)对比可知,优化模型中加号前的部分对应整个模糊系统的模糊熵,这部分在优化过程中能使得整个模糊系统的模糊熵尽可能小;而加号后的部分为增加的约束项,由于1是最理想的隶属度,最小化1-μj(xji)能够在减小整个系统模糊度的情况下同时使各个单独的隶属度函数在各自的论域中尽可能的理想。因此,本文建立的优化模型不但降低了系统整体的模糊度,而且使得每个样本尽量接近它实际所属的论域,这样优化得到的参数使隶属度函数的表述更为客观准确。

2.3.2 基本概率分配函数

基于上述优化得到的模糊隶属度,各证据体的基本概率分配mi(Aj)以及证据体的不确定性描述mi(Θ)分别由式(5),(6)[19]得到

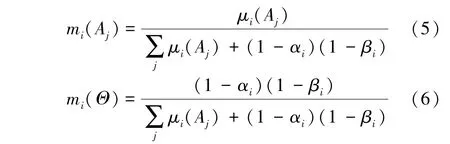
其中,αi为第i个证据体对各命题的隶属度的最大值与次大值的差,该值反映了最大隶属度的突出程度; βi为除去最大值,第i个证据体对其余命题的隶属度的方差,该值反映除最大隶属度外,其余隶属度的集中程度。则有

式中,μi(Am)为第i个证据体对第m个命题的隶属度为最大值;ωi为第i个证据体对各命题的隶属度中除去最大值,对其余命题的隶属度的均值。

2.4 BPA决策准则

在基于证据推理的故障决策方法中,利用组合后的BPA对设备的状态做出评估,需要一定的判定依据。根据如下准则[20],当同时满足这3条时,可确定出诊断结论为命题Am。

准则1表明诊断结论应具有最大的BPA;准则2表明诊断结论的BPA与其他BPA之差要大于某一门限ε;准则3表明证据的不确定度m(Θ)要小于某一门限λ;其中ε,λ根据实际情况取定。

3 实例分析

以某公司生产的PJG9L-630/10(6)系列矿用隔爆型高压真空配电装置为例,其真空断路器永磁操作机构控制器中有2个储能电容(C1,C2),容量均为15 000 μF,分别为合、分闸线圈供电,电气原理如图2所示。

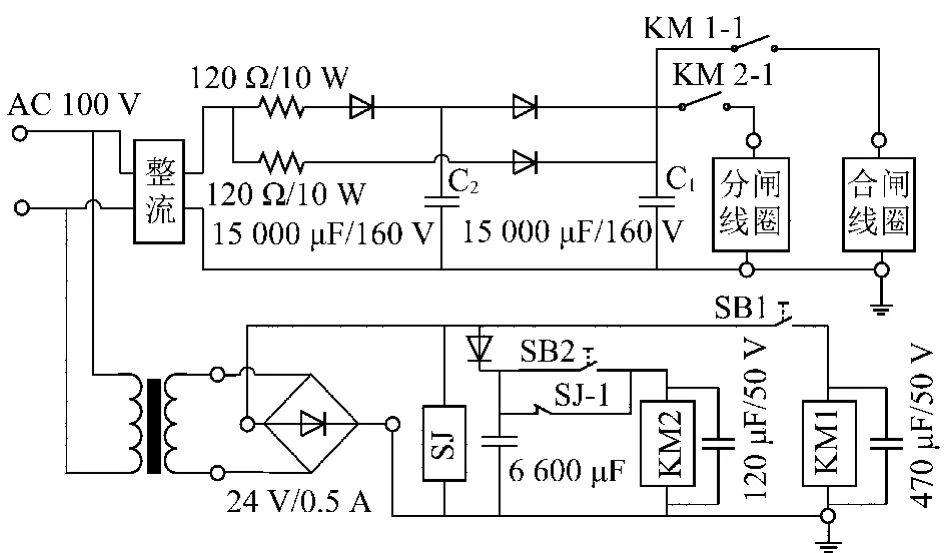
图2 永磁操作机构电气原理Fig．2 Electrical principle diagram of permanent magnetic actuator

在运行现场长期采集储能电容的特征参数值,取其部分作为优化模型的输入样本,见表1,其中ESR和C的值是将现场监测的电容电压与电容电流信号经相关的算法处理后得到的,t则利用充电过程中采样时间间隔与采样点数的乘积来计算。根据多次试验结果和现场运行状况经验已对各特征参数值进行了状态分类,从表1中数据可知,单一证据体的各状态模式(A1,A2,A3,A4)下的数据具有一定的模糊性。

表1 储能电容特征参数样本Table 1 Samples of the storage-capacitor fault features

首先利用Matlab2012b编程实现式(3)所建立的隶属度函数优化模型,根据表1提供的数据,对ESR, C和t的隶属度函数分别求解前述优化问题,最后,对应t1,t2,t3,t4,得到3组参数值分别为tESR=[50, 55．3,70．1,90],tC=[1．45,1．38,1．35,1．33],tt= [3．95,3．82,3．36,3．18],从而得到ESR,C和t的隶属度函数如图3所示。

图3 ESR,C,t的模糊隶属度函数Fig．3 Fuzzy membership function of ESR,C and t

随机抽取储能电容的一组运行状态指标：RESR= 51．3 mΩ,C=13 648 μF,t=3．4 s,根据图3得到这3个证据体对各个命题的隶属度,见表2。将求得的隶属度代入式(5)～(10)中,构造如表3所示的基本概率分配。

表2 各命题的模糊隶属度Table 2 Fuzzy membership degree of each proposition

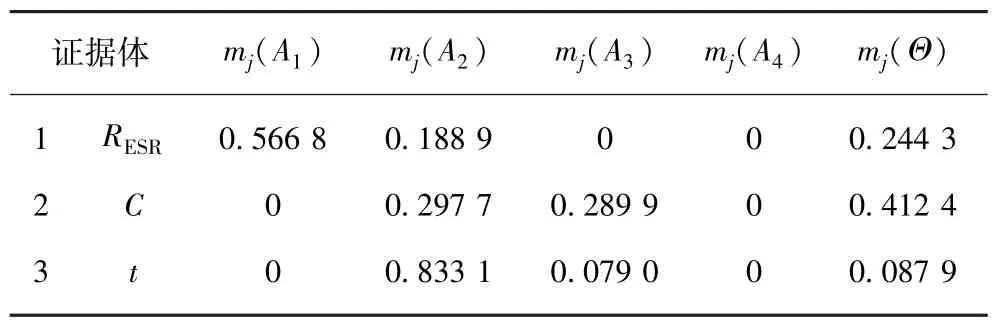
表3 各证据的基本概率分配Table 3 Basic probability assignment function of each evidence

根据证据合成法则(式(5),(6)),计算得到最后的融合结果见表4。

表4 D-S融合结果Table 4 Results of the D-S combination

结合决策准则(ε取0．3;λ取0．2),从表3,4中可以看出,3个子证据体单独作用时,无法得出诊断结果,而由3个子证据融合后的结果可以判断储能电容当前的状态等级为正常;同时可看出,当仅有2个证据体融合时,诊断结果仍有可能存在冲突,如表4中证据1&2的融合结果,其ε明显小于设定值,相比之下,3个证据体的融合结果中m(A2)明显增大而m(Θ)明显减小,即诊断结果的可信度提高,不确定性降低。这表明,多元信息的融合结果具有更好的峰值性和可分性,从而更加全面准确地反映设备当前状态。

4 结 语

基于D-S证据理论的信息融合技术是解决多证据支持下储能电容失效诊断的一种有效方法,该方法能充分利用多元信息,消除多证据间的矛盾与冲突。

本文建立的基于模糊熵的最小模糊度优化模型,以及由此构建的基于模糊隶属度的BPA,避免了经验性赋值的主观性,提高了故障诊断的可信度。较单一故障特征的诊断,全面融合后所得到的决策大大增加了储能电容失效诊断的准确性,有效解决了永磁机构电源系统的可靠性问题,这对确保隔爆开关准确动作以及矿井供电的安全可靠具有十分重要的意义。

[1] 曹文思,郭 恒,巩鲁洪,等．真空断路器永磁操作机构控制器保护电路元件参数优化设计[J]．电力自动化设备,2011, 31(11)：83-88．

Cao Wensi,Guo Heng,Gong Luhong,et al．Parameter optimization of protection circuit for operation controller of permanent magnetic actuator with vacuum circuit breaker[J]．Electric Power Automation Equipment,2011,31(11)：83-88．

[2] 季明忠,李 波．永磁机构真空断路器的应用[J]．煤矿机械, 2009,30(5)：189-191．

Ji Mingzhong,Li Bo．On institutional vacuum circuit breakers permanent magnet crane mine application[J]．Coal Mine Machinery, 2009,30(5)：189-191．

[3] 朱佩龙．具有电容器特性在线检测功能的控制电路设计[J]．高压电器,2003,39(5)：41-43．

Zhu Peilong．A control circuit design with on-line monitoring function of capacitor behavior[J]．High Voltage Apparatus,2003, 39(5)：41-43．

[4] 高 鹏．真空断路器的可靠性研究[D]．大连：大连理工大学, 2013．

Gao Peng．Research on the reliability of vacuum circuit breaker [D]．Dalian：Dalian University of Technology,2013．

[5] 董恩源,刘 罡,邹启涛,等．长行程断路器操动用新型磁力机构[J]．高电压技术,2010,36(3)：816-820．

Dong Enyuan,Liu Gang,Zou Qitao,et al．New type magnetic force actuator(MFA)for long stroke circuit breaker[J]．High Voltage Engineering,2010,36(3)：816-820．

[6] 王新龙,车剑飞．铝电解电容器中气体析出过程的研究[J]．电子元件与材料,2001,20(4)：21-23．

Wang Xinlong,Che Jianfei．Investigation on gas evolution of aluminum electrolytic capacitors[J]．Electronic Components&Materials, 2001,20(4)：21-23．

[7] 陈永真,李 锦．电容器手册[M]．北京：科学出版社,2008．

Chen Yongzhen,Li Jin．Capacitor handbook[M]．Beijing：Science Press,2008．

[8] Vogelsberger M A,Wiesinger T,Ertl H．Life-cycle monitoring and voltage-managing unit for DC-link electrolytic capacitors in PWM converters[J]．IEEE Transactions on Power Electronics,2011, 26(2)：493-503．

[9] Amaral A M R,Cardoso A J M．On-line fault detection of aluminum electrolytic capacitors,in step-down DC-DC converters,using input current and output voltage ripple[J]．IEEE Transactions on Power Electronics,2012,5(3)：315-322．

[10] Abdennadher K,Venet P,Rojat G,et al．A real time predictive maintenance system of aluminum electrolytic capacitors used in uninterrupted power supplies[A]．Industry Applications Society Annual Meeting[C]．2008：1-6．

[11] 何 友,王国宏,陆大金,等．多传感器信息融合及应用[M]．北京：电子工业出版社,2007．

He You,Wang Guohong,Lu Dajin,et al．Multi sensor information fusion and its application[M]．Beijing：Publishing House of Electronics Industry,2007．

[12] 张 鑫,牟龙华．基于信息融合的矿山电网复合保护的研究[J]．煤炭学报,2012,37(11)：1947-1952．

ZhangXin,MuLonghua．Researchoncompoundprotection for mine power network based on information fusion[J]．Journal of China Coal Society,2012,37(11)：1947-1952．

[13] 朱大奇,刘永安．故障诊断的信息融合方法[J]．控制与决策, 2007,22(12)：1321-1328．

Zhu Daqi,Liu Yongan．Information fusion method for fault diagnosis [J]．Control and Decision,2007,22(12)：1321-1328．

[14] 王晓亮,董海鹰,任 伟．基于信息融合的750 kV电网二次设备状态评估[J]．电力系统及其自动化学报,2013,25(1)：40-46．

Wang Xiaoliang,Dong Haiying,Ren Wei．State evaluation of secondary device in 750 kV power grid based on information fusion [J]．Proceedings of the CSU-EPSA,2013,25(1)：40-46．

[15] 谢季坚,刘承平．模糊数学方法及其应用[M]．武汉：华中科技大学出版社,2013．

Xie Jijian,Liu Chengping．Fuzzy mathematics method and its application[M]．Wuhan：Huazhong University of Science&Technology Press,2013．

[16] 肖建于,童敏明,朱昌杰,等．基于广义三角模糊数的基本概率赋值构造方法[J]．仪器仪表学报,2012,33(2)：429-433．

Xiao Jianyu,Tong Minming,Zhu Changjie,et al．Basic probability assignment construction method based on generalized triangular fuzzy number[J]．Chinese Journal of Scientific Instrument,2012, 33(2)：429-433．

[17] 肖建于,童敏明,姜春露．基于模糊证据理论的煤层底板突水量预测[J]．煤炭学报,2012,37(S1)：131-137．

Xiao Jianyu,Tong Minming,Jiang Chunlu．Prediction of water inrush quantity from coal floor based on fuzzy evidence theory[J]．Journal of China Coal Society,2012,37(S1)：131-137．

[18] 王 毅,雷英杰．一种直觉模糊熵的构造方法[J]．控制与决策,2007,22(12)：1390-1394．

Wang Yi,Lei Yingjie．A technique for constructing intuitionistic fuzzy entropy[J]．Control and Decision,2007,22(12)：1390-1394．

[19] 齐 贺,赵智忠,李振华,等．基于多传感器振动信号融合的真空断路器故障诊断[J]．高压电器,2013,49(2)：43-48．

Qi He,Zhao Zhizhong,Li Zhenhua,et al．Fault diagnosis of vacuum circuit breaker based on multi-sensor for vibration signals of fusion [J]．High Voltage Apparatus,2013,49(2)：43-48．

[20] 徐晓滨,文成林,王迎昌．基于模糊故障特征信息的随机集度量信息融合诊断方法[J]．电子与信息学报,2009,31(7)：1635-1640．

Xu Xiaobin,Wen Chenglin,Wang Yingchang．Information fusion algorithm of fault diagnosis based on random set metrics of fuzzy fault features[J]．Journal of Electronics&Information Technology, 2009,31(7)：1635-1640．

Failure diagnosis for storage-capacitor in permanent magnetic actuator of flameproof switchgear based on information fusion

LIU Xiao-ming,MU Long-hua,ZHANG Xin

(Department of Electrical Engineering,Tongji University,Shanghai 201804,China)

When the faults in energy-storage capacitor in flameproof switchgears are diagnosed with single evidence,the diagnostic system has a higher misdiagnosis．To overcome this problem,this paper proposes a capacitor failure diagnosis method based on information fusion theory．Firstly,through analyzing the failure mechanism of storage-capacitor,the feature parameters of capacitor were extracted,and the evidence source for state assessment was then obtained．Secondly,the basic probability assignment for capacitor state was determined according to fuzzy membership functions to avoid the subjectivity of membership assigned with expert experiences,and the membership function parameters were established by a minimum fuzzy optimization model．Finally,the different evidences were integrated by D-S combination rule,and according to BPA decision rule,the condition of the energy storage capacitor in practical operation can be assessed．By using the method proposed and the operation data,the current state of the energy-storage capacitors were obtained,and the evaluation study results demonstrate its effectiveness．

storage-capacitor;failure analysis;D-S evidence theory;fuzzy membership;fuzzy entropy

TD611

A

0253-9993(2014)10-2121-07

2013-09-05 责任编辑：许书阁

国家自然科学基金资助项目(51207110);中国博士后科学基金面上资助项目(2013M531210)

刘晓明(1987—),女,山东烟台人,硕士研究生。E-mail：jiujiu9999@126．com。通讯作者：牟龙华(1963—),男,教授,博士生导师。E-mail：lhmu@tongji．edu．cn

刘晓明,牟龙华,张 鑫．基于信息融合的隔爆开关永磁机构储能电容失效诊断[J]．煤炭学报,2014,39(10)：2121-2127．

10．13225/j．cnki．jccs．2013．1279

Liu Xiaoming,Mu Longhua,Zhang Xin．Failure diagnosis for storage-capacitor in permanent magnetic actuator of flameproof switchgear based on information fusion[J]．Journal of China Coal Society,2014,39(10)：2121-2127．doi：10．13225/j．cnki．jccs．2013．1279