时间域质心频移法估算品质因子Q*

2014-06-07 05:59:50余连勇范廷恩胡光义曹思远王宗俊

西南石油大学学报(自然科学版) 2014年4期

关键词：子波波谱质心

余连勇，范廷恩，胡光义，曹思远，王宗俊

1.中海油研究总院，北京东城 100027 2.中国石油大学（北京）CNPC物探重点实验室，北京昌平 102249

时间域质心频移法估算品质因子Q*

余连勇1，范廷恩1，胡光义1，曹思远2，王宗俊1

1.中海油研究总院，北京东城 100027 2.中国石油大学（北京）CNPC物探重点实验室，北京昌平 102249

品质因子Q是表征地下介质对地震波吸收衰减强弱的参量，是储层预测和油气检测的重要参量。质心法是估算Q值的常用方法，精度和稳定性均较高，但该方法需要计算地震子波谱的质心和带宽，其精度依赖于波谱的提取质量。为避免地震子波谱的问题，提出时间域质心频移法，实现了在时间域估算品质因子Q，其核心是根据子波波形信息在时间域直接估算质心频率和带宽。对于常相位子波，其频谱的质心频率即包络峰值处的瞬时频率；对于Gauss谱子波，其带宽可由包络宽度换算得到（两者乘积为一常量）。当地震子波近似为常相位及Gauss谱时，可在时间域估算质心和带宽，按质心法公式估算Q值，规避了地震子波谱的提取。VSP下行波模型测试及实际资料应用表明，时间域质心频移法是可行可信的。

时间域；质心频移法；品质因子；瞬时频率；带宽

余连勇，范廷恩，胡光义，等．时间域质心频移法估算品质因子Q[J]．西南石油大学学报：自然科学版，2014，36（4）：55–62．

Yu Lianyong,Fan Ting´en,Hu Guangyi,et al．Estimating Quality Factor Q with Time-domain Centroid Frequency Shift Method[J]．Journal of Southwest Petroleum University：Science&Technology Edition，2014，36（4）：55–62．

引言

地震波在地下介质中传播时，能量会发生衰减，造成的因素主要分为两类：非固有衰减和固有衰减。其中，非固有衰减包括几何扩散、反射透射损失、层间颗粒散射等，这种衰减一般认为与频率无关；固有衰减则是地层的吸收作用，频率越高，吸收越严重，同时由于速度频散原因，地震子波的相位发生改变。固有衰减造成地震波主频降低、带宽减小，严重影响了中深层地震资料的成像能力。品质因子Q是表征地层对地震波吸收衰减强弱的常用参量，Q值越小，衰减作用越强。反Q补偿是提高资料分辨率的一种有效手段，需要提取准确的地下Q场。另外，当地层含气时，Q值将变小，呈现出较为明显的异常。因此，Q值的准确估算对于高精度解释、储层预测及油藏描述等具有重要的意义[1]。

常规的品质因子估算方法[2-3]分两大类：时间域和频率域。时间域方法有上升时间法[4]、解析信号法[5]等，可以利用时间信号直接计算，但受资料品质等因素影响较大，而且只能利用局部一小段信息。频率域方法有谱比法（LSR）、质心频移法（CFS）[6-9]、峰值频率法[10-13]等，一般认为频率域方法比较稳定，可靠性高[14-20]。质心法是目前应用较多的Q值估算方法，其利用了频谱的统计属性（质心和带宽），通过两者的解析组合来反演品质因子，具有较好的鲁棒性。武银婷等[21]对质心法进行了测试，认为该方法比频谱比法、振幅衰减法能更加准确识别薄层界面；张大伟等[22]通过模型对比、资料测试等分析认为，质心法的估算结果比谱比法更精确、更可信；赵宁等[23]从数学近似的角度推导了更为严密的属性组合法，与质心法类似，都是基于子波谱的统计属性组合式估算Q值，该方法规避了传统质心法对震源谱的Gauss函数假设，更利于误差控制及理论分析。但频域方法面临的问题是需要提取较为准确的地震子波谱，Q值估算精度很大程度上依赖于波谱的提取效果。

为了避免地震子波谱的提取，提出时间域质心频移法，在时间域信号上直接估算地震子波谱的质心和带宽，再根据质心频移公式估算品质因子Q。最后，利用VSP下行波场的模型记录，测试该方法的可信性。

1 基本原理

Barnes A E[24]指出，对于一个常相位子波a(t)，其包络（由Hilbert变换得到）峰值处的瞬时频率 fs等于其振幅谱A(f)的质心频率 fc

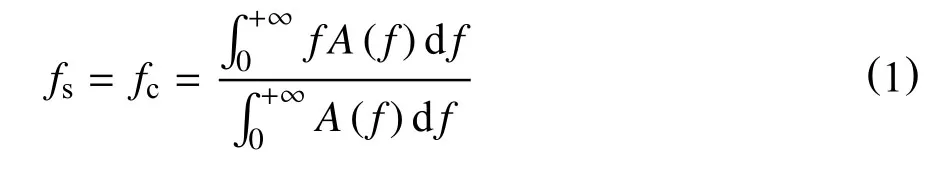
式中：fs—包络峰值处的瞬时频率，Hz；fc—谱的质心频率，Hz。

给定一子波g(t)，其振幅谱记为Gauss谱G(f)

式中：σf—谱的半径（即带宽的一半），Hz。

事实上，Gauss谱具有较好的数学特性，根据Fourier反变换，g(t)的包络亦是一个Gauss函数，定义其中心为

其半宽度为

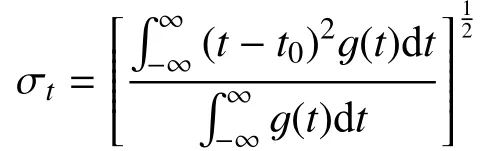
则有如下关系

记地震波传播过程中的初始子波谱为S(f)，衰减子波谱为R(f)，若不考虑相位频散因素，按Futterman模型，则有

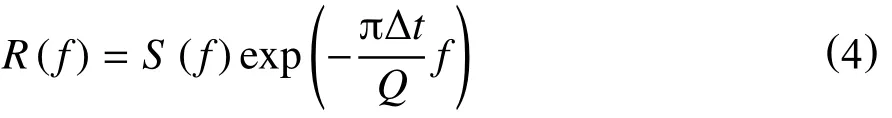
质心频移法利用如下解析式进行Q值反演

式中：

fc1—初始子波谱S(f)的质心频率，Hz；fc2—衰减子波谱R(f)的质心频率，Hz；Δt—子波传播时差，s；Q—传播介质的品质因子，无因次。

对于近似Gauss谱的常相位子波，可以直接在时间域估算其包络峰值处的瞬时频率和包络宽度，联立式（1）、式（3）和式（5），得到Q值估算式

式中：

fs1，σt1—初始子波包络峰值处瞬时频率和半径，Hz；fs2—衰减子波包络峰值处瞬时频率，Hz。

式（6）即为时间域质心频移式。

2 模型测试

2.1 单子波测试

对式（1）和式（3）进行单子波测试，选取的子波谱有Gauss谱和Ricker谱。图1是Gauss谱子波，主频f0为50 Hz，谱半径σf取15 Hz，左图为时间域子波（蓝线为波形，红线为包络），右图为振幅谱（蓝线为振幅谱，“∗”号为质心频率，红色实线间距表示波谱的带宽）。根据时间域复信号，利用式（1）估算出质心频率为50.02 Hz，谱半径为14.94 Hz，与理论值较为接近。图2是Ricker谱子波，主频取40 Hz，图中各曲线说明同图1。根据频率域振幅谱，可计算得到该谱的质心频率为45.13 Hz，谱半径为19.04 Hz；根据时间域复信号，可计算得到质心频率为45.11 Hz，谱半径为18.21 Hz，两组数值较为接近，相对误差在4.50%以内。

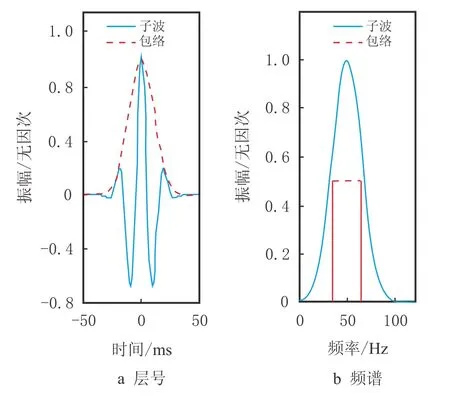
图1 Gauss谱子波Fig.1 Gauss function wavelet

为不失一般性，这里进行了多组不同主频Ricker谱（常相位值随机给定）的测试，分别从频率域和时间域估算质心和谱半径，估算结果见表1。估算结果显示，时间域估算的质心频率与真实值之间的误差在0.15%以内，谱半径误差在4.50%以内。测试结果表明，对于近似Gauss谱的常相位子波，时间域估算的质心频率和谱半径具有一定的可信度。

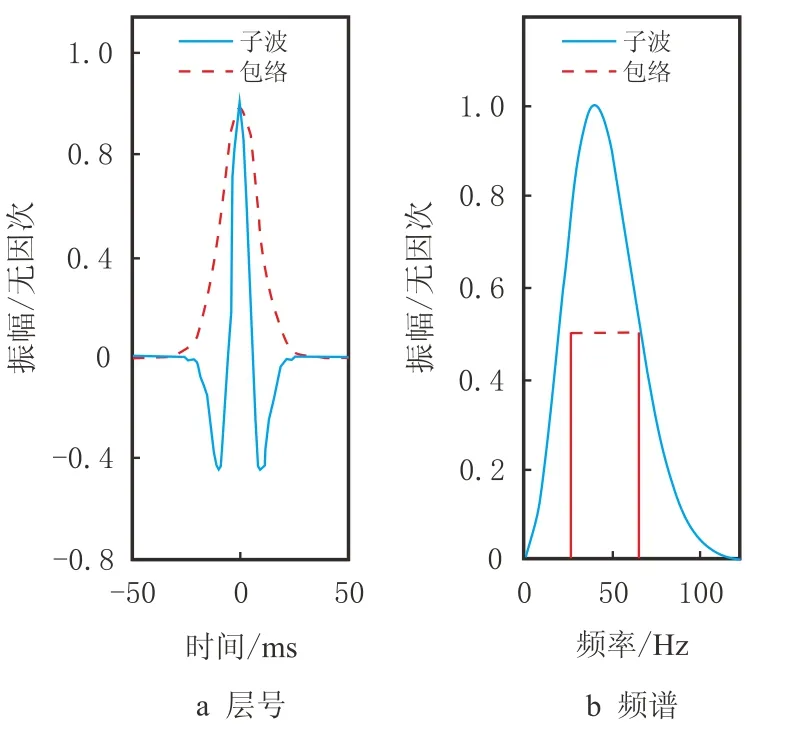
图2 Ricker谱子波Fig.2 Ricker wavelet

表1 不同主频的Ricker子波质心频率和谱半径Tab.1_Centroid frequency and spectral radius of Ricker wavelets with different dominant frequencies

2.2 单层模型测试

设计一单层均匀介质，层速度为2 000 m/s，层厚为100 m，单层旅行时为0.05 s，品质因子为50。初始子波为50 Hz主频的Ricker子波（记为子波1），见图3中蓝色实线，蓝色虚线为其包络；经介质衰减后的子波（记为子波2）见图3中红色实线，红色虚线为其包络。根据时间域质心式可反演得Q值为46.56，接近于真实值50，相对误差在10%以内。如果采用频率域质心法，则反演得Q值为50.92，精度更高。对比两种方法发现，时间域求得的质心差为1.748 0Hz，谱半径为22.763 5 Hz，频率域质心差为1.748 8Hz，谱半径为23.809 7 Hz。试算结果可见，时间域质心式的精度稍低于常规质心法，误差主要来源于谱半径的估算，这是由Ricker谱与Gauss谱差异造成的。式（3）显示Gauss谱时频窗面积（即4σt·σf）为(2π)−1，达到了理论上的最小值（即时频分辨率的极限），常见波谱的时频窗面积一般都大于该值，造成谱半径估算误差。但应该肯定的是，时间域质心法反演的地层Q值，具有一定的可信度。

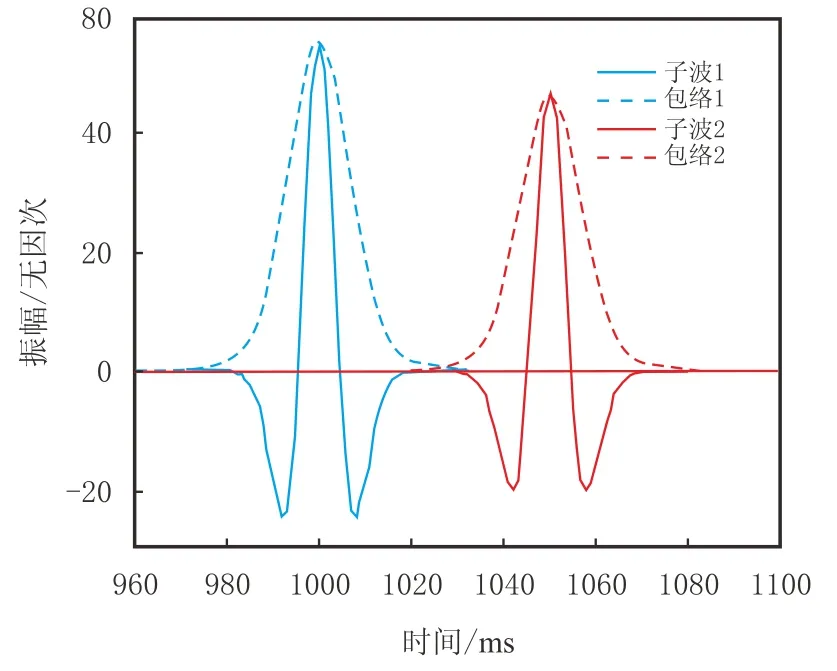
图3 衰减正演记录Fig.3 Attenuation of wavelet

2.3 下行波场测试

设计了一个5层水平介质模型，地层参数见表2。地表初始子波选50 Hz主频的Ricker子波，按式（4）在地层中衰减，检波间距为10 m，得到图4所示的零偏VSP下行波场。根据该下行波场，利用式（4）对相邻道进行Q值反演，由于初始子波为Ricker子波，估算谱半径σf时将式（3）中的(2π)−1改为0.166 5（该值根据Ricker子波的时频窗面积给定）。图5是Q值反演结果，蓝线为真实值，红线为反演值。反演结果较好地反映了地层的Q值走向，在浅层，Q值较准确，随着传播深度的增加，Q值渐渐偏离真实值。图6是相对误差曲线，相对误差在10%以内。如果初始子波时频窗面积未知，仍然按照式（3）估算谱半径，那么反演结果的相对误差将进一步扩大，在8%～12%，但对地层Q值的相对趋势走向影响不大。

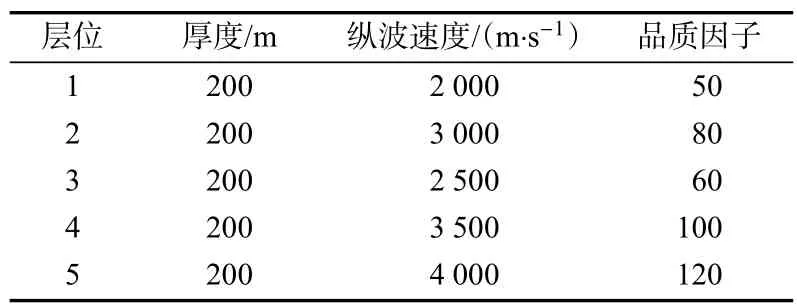
表2 地层参数表Tab.2_Stratum parameters

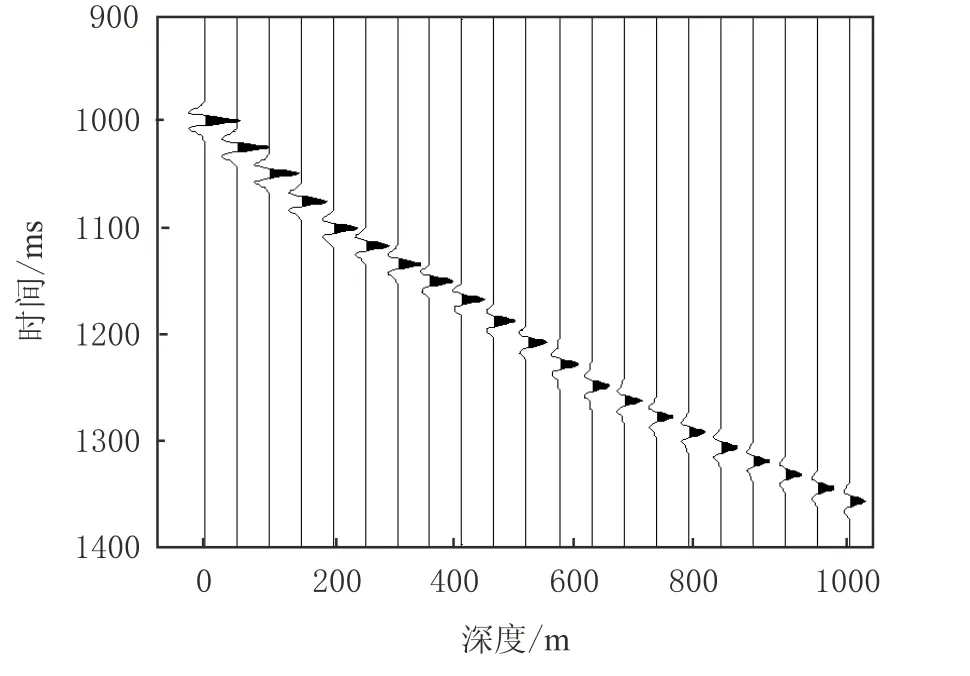
图4 正演下行波场Fig.4 Attenuation of wavelet

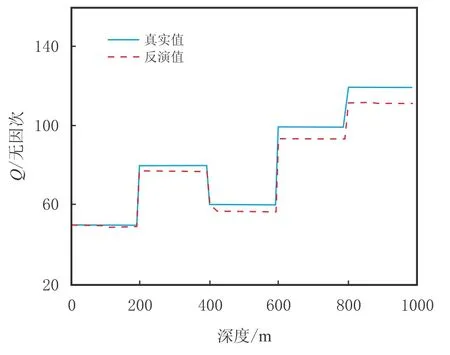
图5 Q值曲线Fig.5 Curve of Q value

图6 相对误差Fig.6 The relative error

3 实际资料处理

图7 VSP下行波记录Fig.7 VSP data

图7是海上一VSP下行波资料，共80道记录，起始深度290 m，最深890 m，前40道检距为10 m，后40道检距为5 m，1 ms采样。利用该下行初至波场，在时间域提取各道初至波的质心频率和谱半径，分别见图8a和图8b，由于实际资料处理中质心和谱半径曲线难免出现振荡现象，这里对局部振荡进行了拟合平滑处理。图9是最终反演的层介质参数，图9a是层速度曲线，分布在2 000～3 200 m/s；图9b是频率域质心法（即常规方法）估算的Q值曲线，分布在50～250；图9c是时间域质心法估算的Q值曲线，分布在50～200。对比频率域和时间域质心法，两者提取的Q值存在一定的差异，图9d为两者的相对差值百分比（以图9b的Q值为标准），相对误差分布在0～25%，这与时间域质心法本身存在一定的理论误差以及质心、谱半径实际估算误差有关；但同时，两条Q值曲线的走向趋势基本保持一致，较好地反映了地层Q值的相对变化，证实了时间域质心法在实际生产中的实用性。对比速度和Q值曲线发现，300～700 m的Q值与速度曲线呈较好的正相关；700～900 m的Q值走向与速度走向不一致，仔细分析原始下行波场纪录以及采用其他Q值估算方法（如谱比法等）后，认为该段Q值趋势是合理的，与速度的不一致可能与该段岩性较为特殊有关。

图8 各深度初至波质心及谱半径Fig.8 Centroid frequency and spectral radius of seismic wavelets in different depths

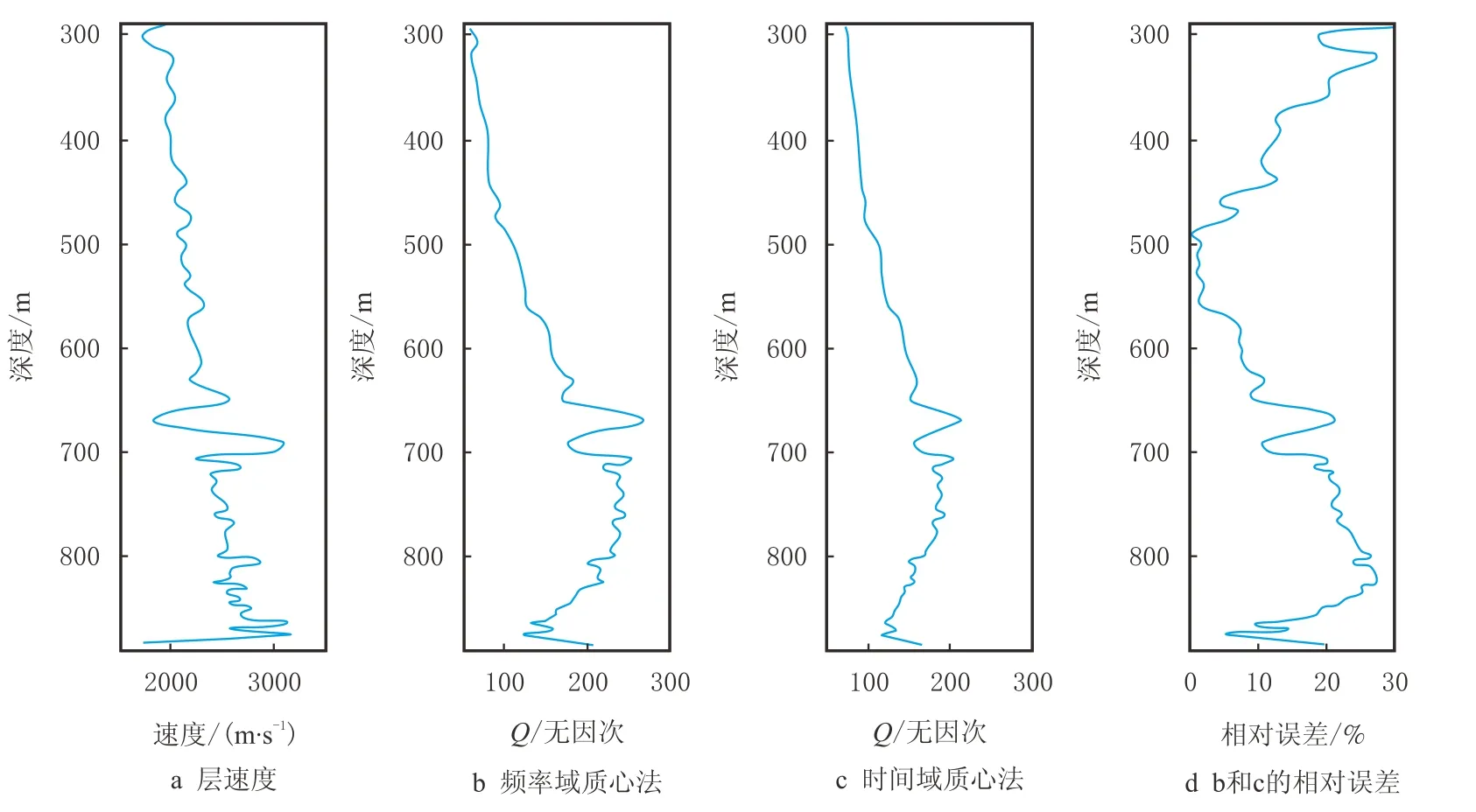
图9 Q值反演结果Fig.9 Q value inversion

图9显示的Q值对应的双程旅行时段约为300～900 ms，利用时间域质心法估算的该段Q值对过井剖面进行反Q补偿，深层Q取恒值120。图10为井旁道补偿前（图10a）、后（图10b）的记录及其对应的时频谱，目的层为1 000～2 000 ms。从补偿前记录的时频谱上可以看到，该海上资料的浅层分辨率较高，高频可达120 Hz，随着深度的增加，主频逐渐降低，带宽变窄，能量降低。记录经补偿后，中深层的主频和带宽增加，分辨率提高，尤其是800～1 400 ms的记录，同时浅中深层的能量分布较为均衡，一致性增强。

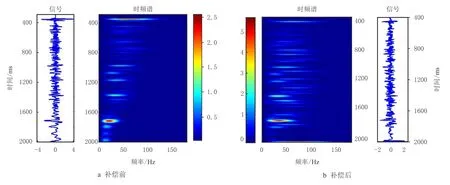
图10 井旁道补偿前、后的记录及其时频谱Fig.10 Signal and its time-frequency spectrum before and after inverse Q filtering

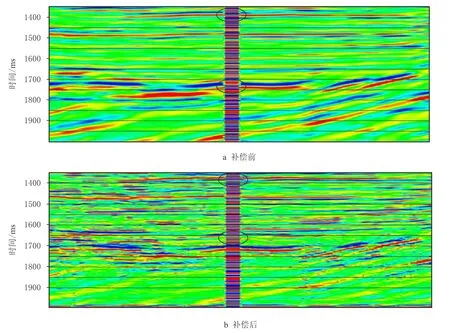
图11 补偿前、后记录的井震匹配Fig.11 Well-seismic matching before and after Q compensation

图11是补偿前（图11a）、后（图11b）的过井剖面对比（1 300～2 000 ms），剖面中嵌入了井上VSP走廊叠加道进行井震对比。可以看到，补偿前剖面的分辨率较低，井震匹配度低；补偿后剖面的分辨率提高，各层能量得到合理抬升，相位得到校正，井井震匹配度增强。对比1 710 ms处的同相轴（见黑框），补偿前井旁道与走廊叠加道极性相反，补偿后两者的一致性增强，横向连续性得到改善。类似的对比还出现在1 380 ms处（见黑框），补偿后的井震匹配度得到显著改善，从侧面验证了Q值估算的合理性和可靠性。

4 结论

（1）时间域质心法规避了初至波谱的提取问题，根据子波包络提取峰值处的瞬时频率和包络宽度，再换算成质心法需要的质心频率和谱半径，实现时间域估算Q值的目的。

（2）与常规质心法相比，时间域质心法可能更依赖于地震子波谱的假设条件（主要是时频窗面积这一因素），这是该方法的不足之处。一般地，地震子波在传播过程中其时频窗面积是变化的，将影响谱半径的准确估计，但对整体Q值趋势走向影响较小。在实际资料的处理过程中，质心频率的估算是很重要的环节，有限的波动将对Q值估算造成较大的影响。

[1]马昭军，刘洋.地震波衰减反演研究综述[J].地球物理学进展，2005，20（4）：1074–1082. Ma Zhaojun，Liu Yang.A summary of research on seismic attenuation[J].Progress in Geophys.，2005，20（4）：1074–1082.

[2]宫同举，孙成禹，彭洪超，等.几种提取品质因子方法的对比分析[J].勘探地球物理进展，2009，32（4）：252–256. Gong Tongju，Sun Chengyu，Peng Hongchao，et al.Comparison of several computational methods of quality factor[J].Progress in Exploration Geophysics，2009，32（4）：252–256.

[3]云美厚，聂岩，李运肖，等.地层品质因子的几种定义及相互关系[J].石油地球物理勘探，2013，48（5）：816–823. Yun Meihou，Nie Yan，Li Yunxiao，et al.Definition and mutual relationship of several quality factors[J].Oil Geophysical Prospecting，2013，48（5）：816–823.

[4]Kjartansson E.Constant Q-wave propagation and attenuation[J].J.Geophys.Res.，1979，84：4737–4748.

[5]Engelhard L.Determination of seismic-wave attenuation by complex trace analysis[J].Geophysical Journal International，1996，125（2）：608–622.

[6]Quan Y L，Harris J M.Seismic attenuation tomography using the frequency shift method[J].Geophysics，1997，62（3）：895–905.

[7]Tu Ning，Lu Wenkai.Improve Q estimates with spectrum correction based on seismic wavelet estimation[J].Applied Geophysics，2010，7（3）：217–228.

[8]James R.Integrated estimation of interval-attenuation profiles[J].Geophysics，2006，71（4）：19–23.

[9]Rainer T.The determination of the seismic quality factor Q from VSP data：A comparison of different computational methods[J].Geophysical Prospecting，1991，39（1）：1–27.

[10]Zhang Changjun，Ulrych T J.Estimation of quality factors from CMP records[J].Geophysics，2002，67（5）：1542–1547.

[11]高静怀，杨森林.利用零偏移VSP资料估计介质品质因子方法研究[J].地球物理学报，2007，50（4）：1198–1209. Gao Jinghuai，Yang Senlin.On the method of quality factors estimation from zero–offset VSP data[J].Chinese Journal of Geophysics，2007，50（4）：1198–1209.

[12]高静怀，杨森林，王大兴.利用VSP资料直达波的包络峰值处瞬时频率提取介质品质因子[J].地球物理学报，2008，51（3）：853–861. Gao Jinghuai，Yang Senlin，Wang Daxing.Quality factor extraction using instantaneous frequency at envelope peak of direct waves of VSP data[J].Chinese Journal of Geophysics，2008，51（3）：853–861.

[13]朱定，陈国俊，蔡成国.利用VSP直达波资料反演粘弹介质的相速度及品质因子[J].勘探地球物理进展，2004，27（5）：337–342. Zhu Ding，Chen Guojun，Cai Chengguo.Inversion of phase velocity and quality factor from direct waves in vertical seismic profile data[J].Progress in Exploration Geophysics，2004，27（5）：337–342.

[14]刘国昌，陈小宏，杜婧，等.基于整形正则化和S变换的Q值估计方法[J].石油地球物理勘探，2011，46（3）：417–422. Liu Guochang，Chen Xiaohong，Du Jing，et al.Seismic Q estimation using S-transform with regularized inversion[J].Oil Geophysical Prospecting，2011，46（3）：417–422.

[15]Reine C，Van der Baan M，Roger C.The robustness of seismic attenuation measurements using fixed and variable–window time-frequency transforms[J].Geophysics，2009，74（2）：WA123–WA135.

[16]Sams M，Goldberg D.The validity of the Q estimationfrom borehole data using spectral ratios[J].Geophysics，1990，55（1）：97–101.

[17]Dasgupta R，Roger A，Clark.Estimation the Q from surface seismic reflection data[J].Geophysics，1998，63（6）：2120–2128.

[18]Wang Y H.A stable and efficient approach of inverse Q filtering[J].Geophysics，2002，67（2）：657–663.

[19]李宏兵，赵文智，曹宏，等.小波尺度域含气储层地震波衰减特征[J].地球物理学报，2004，47（5）：893–899. Li Hongbing，Zhao Wenzhi，Cao Hong，et al.Characteristics of seismic attenuation of gas reservoirs in wavelet domain[J].Chinese Journal of Geophysics，2004，47（5）：893–899.

[20]Hongbing Li.Measures of scale based on the wavelet scalogram with applications to seismic attenuation[J]. Geophysics，2006，71（5）：V111–V118.

[21]武银婷，朱光明，刘伊克，等.零偏 VSP反演 Q值CFS方法及影响因素研究[J].地球物理学进展，2010，25（6）：1897–1904. Wu Yinting，Zhu Guangming，Liu Yike，et al.Study on CFS method in Q inversion using zero-offset VSP data[J]. Progress in Geophysics，2010，25（6）：1897–1904.

[22]张大伟，孙赞东，王学军，等.利用零井源距VSP资料进行品质因子反演[J].石油地球物理勘探，2011，46（增刊1）：47–52. Zhang Dawei，Sun Zandong，Wang Xuejun，et al.Q-factor inversion and calculation using zero-offset VSP data[J].Oil Geophysical Prospecting，2011，46（S1）：47–52.

[23]赵宁，曹思远，胡言防，等.频域统计性属性组合提取品质因子Q[J].石油地球物理勘探，2013，48（4）：545–552. Zhao Ning，Cao Siyuan，Hu Yanfang，et al.Seismic Q estimation by combinations of frequency statistics attributes[J].Oil Geophysical Prospecting，2013，48（4）：545–552.

[24]Barnes A E.Instantaneous spectral bandwidth and dominant frequency with applications to seismic reflection data[J].Geophysics，1993，58（3）：419–428.

编辑：杜增利

编辑部网址：http：//zk.swpuxb.com

Estimating Quality Factor Q with Time-domain Centroid Frequency Shift Method

Yu Lianyong1,Fan Ting´en1,Hu Guangyi1,Cao Siyuan2,Wang Zongjun1
1.CNOOC Research Institute，Dongcheng，Beijing，100027，China 2.CNPC Key Laboratory of Geophysical Exploration，China University of Petroleum（Beijing），Changping，Beijing 102249，China

The quality factor Q is the parameter that characterizes seismic wave energy attenuation caused by underground medium，and it is a key parameter in reservoir predication and hydrocarbon detection.Centroid frequency method is a common method to evaluate quality factor，which has high precision and stability.But this method needs calculation of the centroid frequency and bandwidth of spectrum，which mainly relies on the quality of seismic spectrum.To avoid extraction of wavelet spectrum，time-domain centroid frequency shift method（TCFS for short）is put forward.This method estimates the quality factor by calculating the centroid frequency and bandwidth of seismic wavelet in time domain.Centroid frequency of spectrum of constant-phase wavelet is the instantaneous frequency of its envelope at the peak，and Gauss window bandwidth can be calculated by converting the envelope width（the product of them is constant）.When seismic wavelet approximates to constant phase and Gauss window，we can calculate the centroid frequency and bandwidth in the time domain，and evaluate the quality factor according to the centroid formula，which avoids the extraction of seismic wavelet spectrum.The test of VSP down-wave model shows that the time-domain centroid frequency shift method is feasible and credible.

time domain；centroid frequency shift；quality factor；instantaneous frequency；band width

http：//www.cnki.net/kcms/doi/10.11885/j.issn.1674-5086.2014.03.19.03.html