通过集体备课确立圆锥曲线二轮复习思路

■张恋

通过集体备课确立圆锥曲线二轮复习思路

■张恋

今天的集体备课，我们研讨的主题是：通过对前一阶段学生圆锥曲线学习的学情分析，针对学生出现的问题，讨论一下下一阶段各层次班级圆锥曲线二轮复习的教学方案。

一、高考对圆锥曲线的要求

从圆锥曲线练习卷来分析，这份试卷的选题主要以圆锥曲线的基础题和中档题为主，内容覆盖了高考对圆锥曲线考查的两个方面：

1.客观题重点考查圆锥曲线的定义及应用；圆锥曲线的标准方程；圆锥曲线的基本量（a、b、c、e、p等），还有离心率等问题。

2.解答题考查的是：求圆锥曲线的方程和轨迹方程；圆锥曲线的的几何性质；直线与圆锥曲线的位置关系；范围、最值问题。

二、学情调查情况及反馈

每位老师通过批改学生试卷，对各班学生解题出现的问题进行收集，由詹老师、高老师和我将学生出错较多的试题及解答的错误，挑选出比较典型的错误以及个别大题解法作了一个对比，由何老师制作成表格，现在通过投影呈现部分学生的试卷，来进行反馈和反思。

例如，第14题的主要问题表现在，一是学生求轨迹方程时方法选择不当，二是学生对双曲线的定义把握不准确。

14.求与圆（x+2）2+y2=2外切，并且过定点B（2，0）的动圆圆心M的轨迹方程。

例如第17题主要问题表现在，一是学生不知道条件“为锐角”如何转换，二是转化为余弦定理，计算量较大，三是没有注意Δ>0的限制。

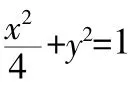
（2）设过定点M（0，2）的直线l与椭圆交于不同的两点A，B，且∠AOB为锐角（其中O为原点），求直线l的斜率k的取值范围。

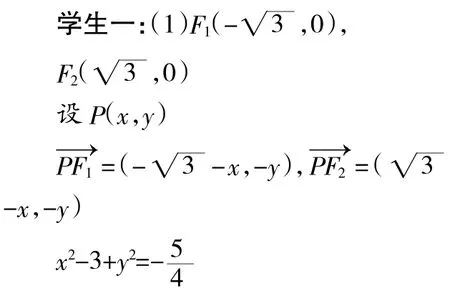
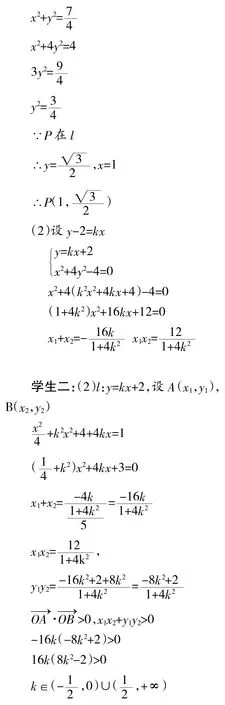
我们几位老师一起总结了一下学生在学习圆锥曲线主要反映出来的问题，有如下几点：

1.对基础知识的理解不扎实，不会应用，其根本原因是学生数学思想欠缺。在基础知识方面，同学们大多都停留在对公式、定理及推理的表面了解和熟悉上；例如解答题第14题不会灵活运用双曲线的定义解题，计算繁琐；用了定义的同学又是一知半解，不注意定义中强调的“差的绝对值”，而忽略了范围。

2.对圆锥曲线与平面向量的结合，不会将条件转化为坐标关系。例如第15（2）、17（2）题，从而造成方法选择不当，思维混乱。

3.对求离心率e取值范围的问题，不会将a、b、c之间的等量关系与不等式关系联系起来，例如第8、第11题。这说明学生在方程与不等式的数学思想、等价转化的数学思想等能力不强。

4.不仔细分析题目，对直线方程的选取没有优化，容易忘记对斜率不存在情况的讨论，以及对△不进行判断，就直接出现韦达定理的结果。

5.解析几何对学生来说最大的困难在于运算量大。学生往往能形成思路，但解题过程当中也会因为运算问题常常被卡住，算不出正确结果来。这体现出学生的基本运算训练没有落实，以及学生对算法、算理的理解和储备不够。

三、后阶段复习的策略与建议

针对以上问题，我认为文理各层次班级，在二轮复习圆锥曲线中的侧重点应有不同，普通班不能完全采取放弃的策略，不重视对解析几何的复习；中间层次的班级也不应放弃一些在能力范围内的题，争取大题中的第2问能动笔；火箭班中的绝大部分同学应力争解析几何大题得10分以上。所以，结合我们这次的学情调查暴露出来的问题，对后一阶段的复习，可采用以下几点建议。

1.进一步强化概念，提高学生应用定义解题的意识。

2.强化数形结合。例如用待定系数法求圆锥曲线方程时，可以数形结合——先定型，再定量。

3.加强基本方法，典型题型的训练。设而不求、整体代换、点差法这些基本方法必须熟练掌握，直线与曲线位置关系、定点、定值、范围等问题必须熟练解题套路。审题时多收集信息，综观全局，权衡利弊，再决定解题策略。

4.突破运算关。直线与圆锥曲线的综合问题一直是高考的热点，解答的关键是坐标化，难点是代数运算和推理，以及参数的处理。而运算能力差是学生普遍存在的问题，课堂上老师要示范计算过程，给足时间让学生自己算，在运算过程中，力求避繁就简。平时教学中，教师要培养学生运算的求简意识，突出解析几何设而不求的运算本色，充分发挥圆锥曲线的定义和利用平面几何知识化难为易、化繁为简的作用。

5.提高学生等价转化的能力。实现复杂问题简单化、陌生问题熟悉化。例如教给学生一些常用的解答策略：①没有图形，不妨画个图形，以便直观思考；②“设——列——验”是求轨迹的通法；③消元转化为一元二次函数（方程），判别式、韦达定理、中点、弦长公式等要把握好；④多感悟“设——列——解”，设什么？可以设坐标、方程、角、斜率、截距。列的前提是找关系，解就是转化、化简、变形，向目标靠拢；⑤紧扣题意，联系图形，数形结合。

6.指导学生对问题进行较深入的思考和横向联系。解析几何可与集合、简易逻辑、函数、方程、数列、三角、平面几何、平面向量、不等式、导数等知识点融合；特别是与新增内容的综合，如线性规划与平面几何的综合，圆锥曲线与向量、导数的综合问题，利用参数方程与极坐标解决圆锥曲线综合问题等。

7.进一步强调表达的规范，解题步骤书写合理（如在求直线方程中，一定要代入原方程进行检验）。

8.根据各班的实际情况有针对性地设立专题，如定义、性质的应用，范围、最值问题，定点、定值问题，存在性问题等。

解析几何题不但能体现考试说明中对运算能力的要求，还能很好地体现个性品质要求：考生要以平和的心态参加考试，合理支配考试时间，以实事求是的科学态度解答试题，树立战胜困难的信心，体现锲而不舍的精神。

（作者单位：武汉市育才高级中学）

责任编辑 王爱民