师范院校学生“导数”内容知识和教学内容知识理解情况的调研

郭玉峰，刘 佳

（1．北京师范大学 数学科学学院，北京 100875；2．北京市通州区运河中学，北京 101100）

师范院校学生“导数”内容知识和教学内容知识理解情况的调研

郭玉峰1，刘 佳2

（1．北京师范大学 数学科学学院，北京 100875；2．北京市通州区运河中学，北京 101100）

借用SOLO分类原理将导数内容知识和教学内容知识的理解分为4个层次水平，通过改编和自编的测试问卷对92名师范院校的师范生进行测试，结果表明：大部分学生处于1-水平和2-水平，在导数内容知识方面缺乏深层次理解，有关导数的存在性、曲线的切线、导数的几何意义、导函数等的理解存在问题，举反例的能力不强；导数内容知识的理解和导数教学内容知识的理解存在显著线性相关；导数教学内容知识的理解存在年级差异．据此建议：增强师范生对数学核心内容本质的理解和把握；加强教育实习、教育见习的指导，提高学科教学知识的理解．

师范生；学科知识；学科教学知识；导数

1 引 言

教师专业发展问题是近年来国内、外研究的热点．按照《国家十二五教育发展规划纲要》的要求，中国将继续推进师范生教育，重视教师教育，建立健全教师专业能力发展的长效机制，提高教师的综合素质．关于如何帮助教师提高专业能力？数学家杨乐院士指出：“要帮助年轻的、经验不多的教师提高他们水平的话，我觉得还是让他们的数学知识能够更加深入一些，数学的修养和水平应该更高一些，这实际上不仅是我个人的看法，也是整个数学界的看法．”[1]这反映了数学家对教师数学学科知识上的要求和期望．

目前师范院校部分学生对未来如何教好中小学数学存在一些误区．如，认为不需要具备多么高深的高等数学的知识就可以教学中学数学，不能有意识地将高等数学知识的学习和中学数学教学联系起来；认为数学学得好一定能教好中小学数学，不太重视师范院校开设的教育类课程，甚至视为形同虚设，“这些话我都懂，还需要开设这样一门课吗”？认为数学就是讲演绎、讲证明，数学就是习题和证明，在数学学科教学知识的积累和储备不够等．为了客观反映师范院校学生数学内容知识和教学内容知识的理解情况，研究者以微积分中的“导数”为载体进行了调研．

以“导数”知识为载体进行考查，基于两点考虑．第一，微积分在数学中处于重要地位．导数是微积分的核心概念，蕴含变化率思想，导数是研究初等函数的一个重要工具并发挥积极的作用．这部分内容不仅在中学数学课程中处于重要地位，在高等数学中也处于基础地位；第二，高中数学课程改革的一个方面是将高等数学的部分内容下放到中学课程中，其中包含了“函数极限、微积分、空间向量等众多知识点”，而导数是微积分的重要内容．

文[2]的研究表明，高中数学教师“导数”的学科知识和学科教学知识存在差异；随年龄、阅历的增长，教师的“导数”知识并非随年龄增长呈上升趋势，而是在30~40岁之间有所下降，但教学知识却随着年龄的增长而逐渐丰富．作为培养未来教师的师范院校数学专业的学生对“导数”内容知识和教学内容知识的理解情况如何？对导数内容知识和教学内容知识理解的相关性如何？是否存在年级差异？这是文章研究的主要问题．

这里的学科知识是“所教学科内容的专门知识”[3]，具体指导数的概念、意义、原理、法则、计算以及导数应用等知识．学科教学知识是“教师将自己所理解的学科知识转化成有益于学生理解的知识”[3]，具体指如何以利于学生理解的方式呈现导数的相关内容知识，以及如何理解和帮助不同学生在导数学习中的误区和困难．关于“理解”的考查，主要借鉴SOLO（Structure Of the Observed Learning Outcome首字母的缩写，意为“观测到学习成果的结构”）分类原理[4]，根据学习者的反应确定相应层次水平．

2 研究框架与方法

2.1 研究框架和研究方法

根据普通高中数学课程标准导数部分的内容[5]，以及大学一年级数学分析[6]的导数内容，确立从导数基本概念、导数意义、导函数、导数应用4个维度考察导数内容知识，为研究导数内容知识与教学内容知识的相关性，以这4个维度的知识点为载体，进一步考察导数教学内容知识．

借用SOLO分类原理，根据问卷作答情况，将导数内容知识和教学内容知识各维度的理解情况分别划分为由低到高4个理解水平（0-水平、1-水平、2-水平、3-水平）：

0-水平：得分属于满分的[0%, 25%)范围内．处于该水平的导数内容知识的理解表现为不能给出题目的解答，也不能给出解答思路；处于该水平的导数教学内容知识的理解表现为不能给出合理、有效的纠正措施和教学设计．

1-水平：得分属于满分的[25%, 50%)范围内．处于该水平的导数内容知识的理解表现为对所给题目有一点认识，但不深刻；处于该水平的导数教学内容知识的理解表现为知道正确答案是什么，但不知如何给学生讲解．

2-水平：得分属于满分的[50%, 75%)范围内．处于该水平的导数内容知识的理解表现为能够给出部分解答或思路，但不太全面；处于该水平的导数教学内容知识的理解表现为知道如何纠正错误答案，但给出的教学设计还有待改善．

3-水平：得分属于满分的[75%, 100%]范围内，处于该水平的导数内容知识的理解表现为能正确、完整地给出解答或思路；处于该水平的导数教学内容知识的理解表现为不仅知道如何纠正学生的错误解答，并能给出好的教学设计．

研究采用问卷测试和访谈相结合的方法．研究之初，为确定导数内容知识的考查维度，对相关专业研究生进行了小范围访谈．研究过程中，每一次测试并阅卷后，选出大约10%的测试对象进行访谈，目的是了解被测者的答题思路和真实想法，包括被测者对问卷感到困难的部分，个人的学习情况，选择教师职业的原因等．整个访谈过程做详细笔录．

2.2 测试问卷的编制

测试问卷分两部分，第一部分是导数内容知识的考察，主要参考Thomas W Judson和Toshiyuki Nishimori相关研究测试题[7]，国内秦德生考查学生导数内容理解水平的相关测试题[8]，以及大学、中学相应教材[5，9]．共12道测试题，各题目考察目的如下：

维度一（导数基本概念）：

题目7：对导数基本概念的了解和理解；

题目4：对导数存在性的理解；

题目3：对函数可导和不可导的理解以及举反例的能力．

维度二（导数意义）：

题目9：对导数物理含义的理解；

题目1：对导数几何意义的了解和理解；

题目11：利用导数几何意义解释现实问题．

维度三（导函数）：

题目2：根据导函数的性质推断原函数的性质；

题目6：用导函数解决物理运动规律问题；

题目8：对导函数和原函数图像关系的理解．

维度四（导数应用）：

题目5：利用导数求解和判断函数的极值点；

题目10：利用导函数解决函数的单调区间和极值；

题目12：利用导数求解生活中的优化问题．

第二部分是导数教学内容知识的考察，主要参考国外研究者V. ISAAC[8]的相关研究．共6道开放性问题，各题目考察目的如下：

维度一（导数基本概念）：

题目2.(1)：根据导数基本概念，分析学生解答；

题目2.(2)：分析学生错误解答的原因；

题目2.(3)：教学导数基本概念的能力．

维度二（导数意义）：

题目4.(1)、题6.(1)：根据导数几何意义和曲线的切线概念，判断学生的解答；

题目4.(2)：分析学生错误解答的原因；

题目4.(3)、题目6.(2)：如何纠正学生的错误解答，并对此知识点进行教学设计．

维度三（导函数）：

题目1.(1)、题目5.(1)：判断学生计算导函数的结果或判断导函数的图像正确与否；

题目1.(2)、题目5.(2)：分析学生错误解答的原因；

题目1.(3)、题目5.(3)：教学导函数的能力；

维度四（导数应用）：

题目3.(1)：根据导数为0的点与极值点之间的关系，判断学生的解答；

题目3.(2)：分析学生错误解答的原因；

题目3.(3)：如何纠正学生的错误解答，并进行教学设计．

2.3 测试对象及问卷的信度分析

考虑到数学教学内容知识的考查，样本选取了某师范院校大三、大四数学师范生．共发放问卷102份，回收100份，有效问卷92份，有效率92%．测试时间为2011年6月和8月，测试由研究者亲自执行，避免被测者在答题过程中的交流和讨论，测试时间80分钟．

采用克朗巴哈（Cronbach）α信度系数法进行信度分析．利用SPSS17.0统计软件进行处理，得到问卷的克朗巴哈α系数为0.834 0，基于标准化的α系数为0.827 8，表明本测试问卷具有良好的稳定性和内部一致性[10]．

3 研究结果

根据研究框架和方法，将学生问卷的不同得分对应不同理解水平，得到如下结果：

3.1 有关导数内容知识和教学内容知识的理解情况

导数内容知识各维度的理解情况如图1．

图1表明，大部分调研学生在导数基本概念、导数意义、导函数以及导数应用这4个维度处于1-水平和2-水平．横向比较发现：4个维度处于3-水平的人数百分比分别是16.3%、19.57%、13.04%以及16.3%．

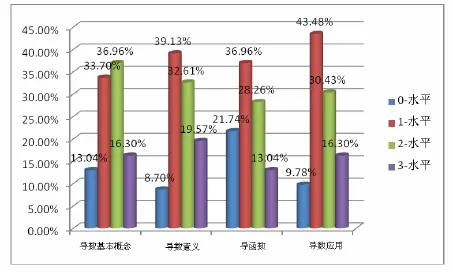
图1 关于导数内容知识各维度的理解水平分布

导数教学内容知识各维度的理解情况如图2．

同样，大部分调研学生导数教学内容知识处于1-水平和2-水平．与导数内容知识的理解情况相比，处于0-水平的人数较少，处于3-水平的人数相对较多．

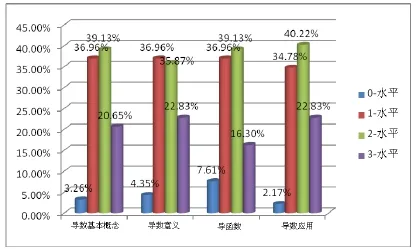
图2 关于导数教学内容知识各维度的理解水平分布

3.2 导数内容知识和教学内容知识理解的相关性分析

为定量描述导数内容知识与教学内容知识理解情况的相关性，分别计算4个维度的相关性．以导数基本概念为例，将所有学生在此维度的得分设为x，教学内容知识相应维度得分设为y，由此得到92对样本值(x1,y1), (x2,y2), …, (x92,y92)，计算其相关系数：

其中

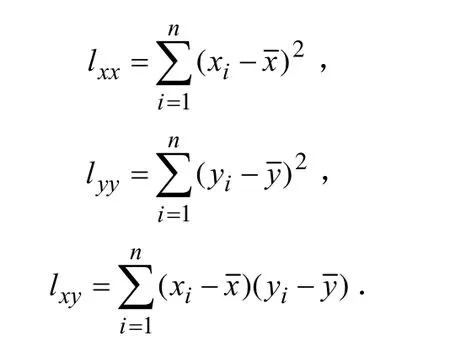
利用excel软件计算两者相关系数为0.35．同理，其它维度相关系数如表1．

表1 导数内容知识与教学内容知识对应4个维度间的相关系数

进行相关系数显著性检验，样本n=92，自由度为n-2=90，取α=0.05，查相关系数临界值表[10]，临界值在n-2=90时的值为0.205 0．由上表相关系数r分别为0.35、0.25、0.33、0.29均大于临界值，说明在α=0.05水平上r是显著的．以上说明，导数内容知识与教学内容知识的理解存在显著线性相关．

3.3 有关导数内容知识和教学内容知识理解情况的年级差异

利用T检验说明调研学生关于导数内容知识和教学内容理解的年级差异．T检验结果如表2：（小括号内数字代表统计临界值，小括号外数字代表检验统计量t．）

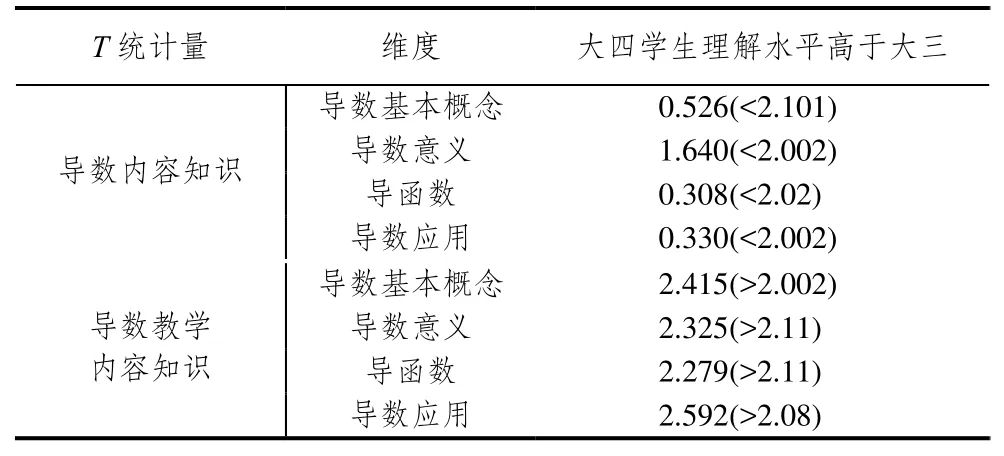
表2 检验统计量T值表

检验统计量t大于临界值，表示存在显著性差异，检验统计量t小于临界值，表示不存在显著性差异．可见，关于导数内容知识的理解，大三、大四调研学生不存在显著性差异；关于导数教学内容知识的理解，大四调研学生理解情况好于大三．

4 研究结果的讨论与分析

从以上数据，可以得到如下主要结论：

4.1 部分调研学生在导数内容知识方面缺乏深层次理解且举反例能力欠缺

数据结果表明，调研学生对导数内容知识的理解大部分（约70%）处于中等水平（即1-水平、2-水平），他们仅能给出部分解答，解答还不全面．具体表现为：了解导数基本概念，但不能举反例判断导数的存在性；知道导数的物理意义和几何意义，但还不能利用其正确求解曲线的切线方程，也不能解释物理现象；知道导函数和原函数图像或性质之间的关系，但不能利用导函数的性质求解物理问题；能利用函数的导数求解极值问题和单调区间，但不能准确解答最优化的应用问题．从横向数据比较发现，导数基本概念、导数意义、导函数及导数应用处于较高水平（2-水平、3-水平）的人数百分比分别是53.26%、52.18%、41.3%以及46.73%．可见，调研学生掌握较好的是导数基本概念，出现问题较多的是导函数有关内容．

进一步访谈发现，调研学生对导数内容知识的深入理解还不够．如部分学生尽管知道导数基本概念，但理解还只限于表面，缺乏深层次的理解．导数内容知识考察的题目4是一道选择题，考察在分段函数的分界点是否存在导数，以及对左右导数的理解．原题如下：设

A. 左、右导数都存在．

B. 左导数存在，但右导数不存在．

C. 左导数不存在，但右导数存在．

D. 左、右导数都不存在．

与文[2] 75%的教师答题错误的调研结果相比，这次调研表明，师范生仍有近约一半答错，错误率仍然较高．可见，部分师范生仍需要进一步深入理解导数概念，对左右导数的概念，以及函数在某一点的导数存在与单侧导数的关系需进一步学习，包括举反例的能力需进一步加强．

部分调研学生对曲线的切线定义、导数的几何意义理解不深刻．有关“导数意义”考察的题目1，“设函数，请问y轴是f(x)在原点的切线吗？说明为什么”，此题考察对导数几何意义的理解，涉及曲线的切线的概念．学生初中阶段学习了直线和圆相切，圆的切线即“直线与圆只有一个公共点，我们就称这条直线是该圆的切线”[11]．在高中，人教版课本中，切线概念有了更广泛的定义，“当点B沿曲线趋近于点A时，割线AB绕点A转动，它的最终位置为直线AD，这条直线AD叫做曲线在点A的切线”[12]，教材给出的图示中，曲线位于切线同侧．有些调研学生未能正确解答该题，一个原因受先前知识的影响，对曲线的切线理解不清导致．以下是部分学生的访谈：

生2：“y 轴不是f(x)=x3在原点的切线．如果是切线，那么曲线应该在切线同侧，并且只有一个公共点，因此原点只不过是一个拐点．”

生3：“我认为y 轴应该是f(x)=x3在原点的切线．因为只有一个公共点．”

实际上，根据曲线的切线定义，“在曲线y=f(x)上一点P(x0,y0)（y0=f(x0)）处的切线，是割线PQ，当Q(x,y)沿曲线趋近于P时的极限位置”，函数在某点处不可导，对应曲线在该点处仍有可能存在切线．根据定义，y轴是该函数f(x)在原点的切线．生1显然认为必须导数存在才有对应切线，这也是很多调研学生出错的主要原因．生2混淆了拐点和切点的概念，误以为曲线必在切线的同一侧，且曲线只能和切线有一个交点（生3也认同这一点）．生2、生3受初、高中切线定义的影响，没有认识到只有二次曲线与直线相切时才只有一个公共点．由于对曲线的切线概念理解不清，对函数在某点处的导数就是曲线在该点处切线的斜率这一导数的几何意义认识不深刻，导致调研学生对此问题的错误解答．

“导函数”考查结果表明，这是调研学生掌握最薄弱的地方．考查导函数的性质的题目2，要求根据导函数的周期性推断原函数的周期性．判断“若f′(x)为周期函数，则f (x)亦是周期函数”这个命题的正误，并给出理由．此题大部分调研学生未能给出正确判断，或是给出正确判断却未能给出正确理由．事实上，这个命题是错误的，可以列举出许多反例，比如“f′(x)=cos x+1是周期函数，但f(x)=sinx +x不是周期函数”．这反映部分调研学生在导函数性质的理解上存在缺陷，不能很好掌握导函数与原函数的关系，举反例的能力需进一步加强．

有关“导数应用”的考察，一方面是利用导数求解函数相关的问题，另一方面是利用导数求解生活中的优化问题．测试结果表明，调研学生可以较好理解具有一定生活背景的题目，但是对于处理利用导数求解函数题目，比如利用导数求解复杂函数的单调区间和极值问题，“求函数f(x)=xlnx-x的单调区间和极值？”等存在一些问题．

4.2 导数内容知识的理解影响到导数教学内容知识的理解

数据结果表明，导数内容知识和教学内容知识的理解存在显著线性相关．有关导数教学内容知识的考察，尽管处于0-水平的人数较少，但仍有约35%的调研学生处于1-水平，他们不知道如何给学生讲解．进一步分析调研结果，发现导数内容知识的理解影响到教学内容知识的理解．

如考察“导函数”教学内容知识的题目5，“设f′(x)是函数f(x)的导函数，f′(x)的图像如右图所示，则f(x)的图像最有可能的选项是左边哪一个（ ）．

这个题目，你的一位学生给出的答案是选项B．

（1）你认为该学生的解答正确吗？

（2）你认为该学生在解答这个问题时是如何思考的？你觉得学生出现以上思考的原因是什么？

（3）你将如何纠正学生的错误想法？”

回答此问题，首先要根据导函数的图像特征判断原函数图像的走势，考虑区间段(-∞,0)，(0,1)，(1,2)，(2,+∞)．导函数图像在(-∞,0)位于x轴上方，判断原函数在此区间段单调递增，排除B、D；导函数图像在(0,1)位于x轴下方，判断原函数在此区间段单调递减，排除A，答案应该是C．可见，答对此题的关键是清楚原函数与导函数的关系，这里学科知识理解的正确与否直接影响到该题的解答．

与上面问题相关的“导函数”内容知识考察的题目8，“下图给出了运动物体的位移、速度和加速度，作为时间t的函数图像，请指出1号、2号、3号哪个图像是位移、速度或加速度．1号图像代表____．2号图像代表____．3号图像代表____”

解答此题的关键是：根据速度是位移关于时间的导数，加速度是速度关于时间的导数．通过逐一排除法，可判断3是位移，2是速度，1是加速度．这里也考察了原函数与导函数的关系，只有清楚判断原函数图像和导函数图像的关系，才能正确解答这两个问题．调研数据显示，后一题得分低的学生在前一题的得分也很低．

又如，“导数意义”教学内容知识考查的题目6，要求分析学生认识上的错误，“某学生认为，‘瞬时速度是无限小的一段时间内的平均速度’，你认为该学生的理解对吗？该生给出这种认识的原因是什么？如果你是老师，你将如何向学生解释导数的基本概念？”回答此问题，关键对导数与瞬时速度的关系，什么是瞬时速度等内容知识有正确、深刻理解．与此对应的“导数意义”内容知识考察的题目9，“一辆法拉利赛车在笔直的马路上行驶，已知路程S是时间t的函数S =4t2+t-1．（1）试求从t=20到t=20+b之间赛车的平均速度？（2）求当b=0.001、0.01、0.1时赛车的平均速度？（3）求赛车在t=20时的瞬时速度？”数据结果表明，题目9（3）出错的学生，在题目6中也答错．

4.3 不同年级学生导数教学内容知识的理解存在差异

T检验结果表明，关于导数内容知识的理解，大三、大四师范生不存在显著性差异；关于导数教学内容知识的理解，大四学生的理解情况好于大三学生．进一步访谈了解到，大四免费师范生曾参加过教育实习、教育实践活动，教育实习中他们经常对任教学生的情况进行分析，对学生错误原因以及改进建议进行思考和讨论．大三师范生未参加过教育实习，即使部分学生有校外家教的经验，但毕竟面对的群体单一、教育实践活动相对匮乏，对分析学生错误原因以及提出纠正学生错误的建议都存在明显的不足和困难．可见教学经验和教学实践活动有助于免费师范生提高数学教学内容知识的理解．

正如数学家杨乐院士所提，提高教师的教学内容知识，首要的是提高他们的数学素养和数学水平．研究表明，师范院校学生在“导数”内容知识的理解方面存在一些问题，在“导数”教学内容知识的理解方面还需进一步增加实践经验，提高分析问题和解决问题的能力．据此，提出几点建议：

（1）增强师范生对数学核心内容本质的理解和把握．

研究发现，部分师范生对导数概念、导数意义的理解存在表面性，不能真正理解其本质；不能清楚认识导函数与原函数的关系；举反例的能力不强．如，学生能够求简单函数的极限、导数，但对导数概念的本质理解模糊甚至不清，对某些基本概念认识不清，如“函数在一点处可导”与“函数在一点处连续”等，还有学生将曲线“过某点的切线”和“在某点的切线”混为一谈．这与文[2] 65名高中数学教师的调研结果有一致之处，如对导数定义深层理解欠缺、对左右导数的概念理解不全面等．

对数学内容本质的认识不清，既会影响到后续数学内容的学习，也可能影响到后来中学数学的教学．中学数学教学，首要的是有良好的数学素养和数学专业水平，也即深入理解数学的学科知识．调研表明，数学学科知识和数学学科教学知识显著相关，遗憾的是，部分师范生对“导数”内容知识的理解仍然存在很多问题，不能很好地理解导数概念的本质和意义，不能清楚认识导函数和原函数的关系，这不能不使人担忧其后的中学数学教学工作．

这种情况的出现，有学生自身的原因，也有师范院校教学中的一些问题．如访谈中发现，部分学生认为当一名中学数学教师无需太高深的数学知识基础，对数学内容知识和教学内容知识的相关性认识不深刻，这种观点导致学习热情不高，学习态度不端正，影响了学习效果．其次，由于高校扩招导致学生整体素质下降，学生已有的数学基础知识不牢固，对数学内容的本质理解不到位，数学素养和数学功底存在的一些问题等也影响到高等数学的进一步学习．就高等师范院校教学而言，主要在于不能将初等数学和高等数学有机结合．调查访谈发现，部分师范生在学习大学微积分导数知识时，认为这只是高中课程导数内容的重复，忽略了对导数本质的进一步理解．

为此，师范院校应加强学生对数学核心内容本质的理解和把握．教师应加强对某些重要、基本概念的深入浅出的讲解，应通过适当的教学途径和方法、以学生易于理解的方式进行教学．高等数学概念教学同样需要形象、直观，需要讲清楚来龙去脉，讲清楚概念与概念间的关联，只有这样，才能使学生把握内容的本质，真正理解内容．

（2）通过教育实践、教育见习等增强师范生的学科教学知识．

调研表明，师范生的“导数”教学内容知识存在年级差异，主要分歧在于是否参加过教育实践，大四师范生的教育实习等经历提高了他们的学科教学知识．因此，教学实习、实践工作对师范生后来的中学数学教学工作非常重要，师范院校应重视教育实习、实践工作的指导．

目前，师范院校师范生的课程设置主要包括3类：通史教育课程、专业教育课程和教师教育课程．教师教育课程直接面向免费师范生未来的教学工作，但往往因为师范生缺乏教学实践经验，对相关课程不能很好领会和学习．只有在经历了教育实习，遇到教学实践中的问题时，师范生才能体会已经学过的课程设置的重要性．为此，高等师范院校应重视教育实习、实践工作的指导，考虑教育实习与教师教育课程合理安排，使学生体会学有所用，激发学习热情，提高学习动力．针对教育实习时间短、形式化、不重视、不规范等一些问题，师范院校可以考虑不同年级进行不同内容的教育见习、教育实习工作，如大学一年级进行“了解性见习”，大学二年级、三年级进行“参与式见习”，大学四年级进行“教育实习”，在实践中感悟学习的乐趣和重要性，改善目前师范生存在的一些现实问题．

总之，“导数”是高中学生已经接触，大学一年级继续深入的内容．调研发现，师范生仍有一部分不能很好理解相关内容，包括相应教学内容．为此，注重学科知识的深入理解，以促进学科教学知识的理解；注重教育实习、实践活动，以促进学科教学知识的理解，相应带动学科知识的学习，这应是解决目前部分师范生学习目的不明确、学习热情不高、学习动力不足的举措之一．

[1] 杨乐．谈谈数学的应用与中学数学教育[J]．课程·教材·教法，2010，（3）：3-9．

[2] 徐芳芳．高中数学教师的学科知识与学科教学知识研究——以导数知识为例[J]．数学教育学报，2011，20（3）：71-75．

[3] Shulman L S. Those Who Understand：Knowledge Growth in Teaching [J]. Educational Researcher, 1986, 15(2): 4-14.

[4] Biggs J, Collis K. Evaluating the Quality of Learning: the Solo Taxonomy [M]. New York: Academic Press, 1982.

[5] 中华人民共和国教育部．普通高中数学课程标准（实验）[M]．北京：人民教育出版社，2003．

[6] 邝荣雨．微积分学讲义（第一册）[M]．北京：北京师范大学出版社，2005．

[7] Thomas W Judson, Toshiyuki Nishimori. Concepts and Skills in High School Calculus: An Examination of a Special Case in Japan and the United States [J]. Journal for Research in Mathematics Education, 2005, 36(1): 24-43.

[8] 秦德生．学生对导数的理解水平及其发展规律研究[D]．东北师范大学，2007．

[9] 中学数学教材实验研究组．普通高中课程标准实验教科书（数学选修2-2B版）[M]．北京：人民教育出版社，2007．

[10] 薛薇．SPSS统计分析方法及应用[M]．北京：电子工业出版社，2010．

[11] 课程教材研究所中学数学课程教材研究开发中心．义务教育课程标准实验教科书（数学九年级上册）[M]．北京：人民教育出版社，2007．

[12] 中学数学教材实验研究组．普通高中课程标准实验教科书（数学选修2-2B版）[M]．北京：人民教育出版社，2007．

Study on the Derivative Content Knowledge and Pedagogical Content Knowledge

GUO Yu-feng1, LIU Jia2
(1. Beijing Normal University, Beijing 100875, China; 2. Yunhe Middle School, Beijing 101100, China)

Based on SOLO Taxonomy, students’ understanding of derivative content knowledge and pedagogical content knowledge can be divided into four hierarchical divisions. The results from researcher-developed student questionnaires indicate that most tuition-free student teachers are in stage-1 or stage-2; the results indicate that derivative content knowledge is significantly correlated to pedagogical content knowledge; and the understating of pedagogical content knowledge for undergraduate four-year tuition-free student teachers are better than that of the three-year tuition-free student teachers. Accordingly, tuition-free student teachers should improve their own understanding, for normal schools should strengthen the guidance of the education practice.

tuition-free student teachers; content knowledge; pedagogical content knowledge; derivative

G420

：A

：1004–9894（2014）01–0057–06

[责任编校：周学智]

2013–10–06

北京市教育科学“十二五”规划重点课题——“四基”之数学基本活动经验研究：量化与课堂实践（ABA12020）

郭玉峰（1972—），女，副教授，博士，全国数学教育研究会理事，主要从事数学课程及学生数学学习研究．