数学专业本科生自我导向学习能力的现状调查与分析

丁亚元，王 敏，陈克胜

（1．安徽广播电视大学 教育科学学院，安徽 合肥 230022；2．安徽大学 数学科学学院，安徽 合肥 230601；3．安徽师范大学 数学计算机科学学院，安徽 芜湖 241000）

数学专业本科生自我导向学习能力的现状调查与分析

丁亚元1，王 敏2，陈克胜3

（1．安徽广播电视大学 教育科学学院，安徽 合肥 230022；2．安徽大学 数学科学学院，安徽 合肥 230601；3．安徽师范大学 数学计算机科学学院，安徽 芜湖 241000）

对数学专业本科生自我导向学习准备度量表进行修订，探讨数学本科生自我导向学习的现状．结果表明：数学本科生自我导向学习准备度量表具有5因素结构，该量表具有良好的信效度；数学本科生自我导向学习准备度处于中等偏上的水平；在不同因素上存在显著的性别、年级差异．在数学专业教学中，应加强数学本科生自我导向学习策略的辅导；注重数学本科生大学适应性教育；开展各种数学实践活动，提高学生创造性解决问题的能力．

数学专业；本科生；自我导向学习；现状调查；分析

1 引 言

随着高等教育由精英化向大众化发展，高校的招生规模有了较大的增长，随之而来的是生源质量下降，学生差异扩大，教学起点难以确定等负面影响．而对大学数学本科专业而言，不仅存在上述问题，还存在着专业内部的问题，如课程内容抽象性强、逻辑性高、推理严密，课程体系结构不尽合理，教学方法和手段陈旧，忽视学生应用意识和创新能力的培养等，这些问题造成了大学数学专业本科生学习困难的现象．有调查显示，数学本科生学习现状不容乐观，学习的突出特点是“被动应付”，课前能做到自主学习的学生比例较小，多数学生缺乏独立思考[1]．大学生自主学习能力的培养，不仅是大学生在校期间学好知识的需要，也是人的可持续发展的需要．在终身学习的背景下，教师不可能、也没有必要把知识全部教给学生，而帮助学生掌握学习的方法、特别是掌握终身学习的方法才是教师的明智选择[2]．

自我导向学习（Self-Directed Learning）是一类特殊的自主学习方式，其概念来源于成人教育领域，最早由塔福（Tough, A. M.）[3]提出，20世纪60年代在世界教育领域内迅速发展并得到广泛使用．所谓自我导向学习，是在学习者的独立性、自觉性和批判性思维的指导下，自觉确立学习目标，拟订学习计划，寻找学习资源，从事学习活动，评价学习结果的过程[4]．Guglielmino L. M. 认为自我导向的学习是一种人格特质，即学习者的态度、价值观与能力；高度自我导向学习者具备主动性、独立性、对学习的坚持性、对自我的学习负责、好奇心、有自信心、喜爱学习、目标导向等特性[5]．自我导向学习具有自主性、灵活性和普遍性、终生性等特点[6]，其要义在于让学生成为“有责任感的学习者”，使学生能够独立从事高效学习、提升学习品质；同时，在学习过程中促成学生人格的成长，并形成相应的社会生活能力．近年来，国内外研究者开始尝试将自我导向学习的研究延伸到基础教育和高等教育领域，并关注其对青少年学业及人格发展的意义．

基于自我导向学习对学生学习和发展的重要意义，以大学数学与应用数学专业本科生为研究对象，通过对现有自我导向学习准备度量表的修订，探讨数学本科生自我导向学习的结构与特征，以期进一步探索数学本科生自主学习的方法与途径．

2 研究方法

2.1 研究目的

探讨数学本科生自我导向学习准备度的结构与差异性特点，采用定量分析的方法，主要从以下两个方面进行研究：数学专业本科生自我导向学习准备度的因素分析，以及数学本科生自我导向学习能力的发展水平与差异性特点．

2.2 测量工具

测量工具为自我导向学习准备度量表．Guglielmino首先于1977年开发了“自我导向学习准备度量表”（Self-Directed Learning Reading Scale，简称SDLRS），用来测量学习者进行自我导向学习的能力[5]，该量表包含58个题项，8个因素．1995年，台湾学者邓运林对Guglielmino的SDLRS进行翻译和修订，修订后的量表包含55个题项，8个因素，各因素分别为：秉持学习机会的开放性8题，效率学习者8题，主动且独立学习7题，对自我学习负责6题，热爱学习6题，创造性6题，看待未来采取正向、乐观8题，掌握基本研读技巧和解决问题的能力6题[7]．该版量表采用李科特5点计分法，测得的总分就是自我导向学习准备度，总分越高表示学生的自我导向学习能力越高，在台湾地区被广泛使用．

研究者先对邓运林版SDLRS中各题项的语句措辞进行修改，使其适合于大陆地区的语言表达习惯．之后，将修改过的邓运林版SDLRS对10名数学本科生进行了初测，找出学生认为表述不清或不易理解的题项，再次进行修改，以此作为数学本科生自我导向学习量表修订的基础（见附录）．

2.3 研究对象

采用分层随机抽样法确定样本．首先，选取安徽省A、B、C三所本科高校的数学与应用数学专业08、09、10、11四个年级的学生为调查对象，其中，A为非师范类211重点大学，B为师范类省属重点大学，C为师范类省属普通本科院校．共发放问卷360份，回收341份，回收率94.7%；剔除无效问卷11份，最终得到有效问卷330份，有效率96.8%．其中男生136人（41.2%），女生194人（58.8%）；大一学生91人（27.6%），大二学生88人（26.7%），大三学生81人（24.5%），大四学生70人（21.2%）．

2.4 数据处理与分析

首先对自我导向学习准备度量表进行项目分析、探索性因素分析和信度、效度检测，然后对数学本科生自我导向学习能力的发展水平与特征进行差异性检验．利用Excel与SPSS19.0进行数据的录入、整理与分析．

3 研究结果

3.1 量表修订

3.1.1 项目分析

求出所有施测量表55个题项的临界比，采用高分组和低分组均值比较（分割点为27%，决断值t≥3，p＜0.05），删除不当题项，剩余53个题项．

3.1.2 探索性因素分析

检验结果表明，受试样本的KMO值为0.82，Bartlett球形检验统计量为5 611.025（df =1 378，p=0.000），说明数据适合做主成分因素分析．

采用主成分分析，抽取了16个特征值大于l的公共因素，累计解释总方差为62.064%．结合碎石图发现，提取3~6个公共因素较为适宜．借助方差极大旋转法，同时根据以下标准删除不适合的题项：① 删除在两个或两个以上公因素上具有相近载荷的题项；② 删除因素载荷小于0.35，共同度小于0.20的题项；③ 某个公因素下只有1个题项．经过数次探索，发现5个因素更利于解释，最终得到数学本科生自我导向学习准备度的5因素结构，共计40个题项，累计贡献率为41.048%．

3.1.3 因素确定及命名

根据修正后量表各因素所包含的具体题项内容重新对因素进行矫正，将5个因素分别命名为终身学习、独立学习、问题解决、积极学习和热爱学习．其中终身学习是指学习者具备终身学习数学的愿望，喜欢展望未来，对新事物充满好奇心；独立学习是指学习者具备独立学习数学的能力，并能对自己的数学学习负责任；问题解决指不仅有解决数学问题的能力，更能创造性地解决问题；积极学习指学习者能够积极主动地参与数学学习活动并能产生积极的结果，可以接受别人的评论或自我评论；热爱学习指学习者对数学学习有强烈的渴望，并享受学习的成果．各因素分析指标详见表1．3.1.4 信度和效度分析

修订后的总量表和5个因素的克隆巴赫系数分别为0.887、0.824、0.783、0.729、0.707、0.716，由此可以看出量表的内部一致性颇佳，信度较高；5个因素与总量表的相关系数分别为0.770**、0.803**、0.658**、0.571**、0.706**，各相关系数均达到中高度显著相关，说明量表具有较好的内容效度．

表1 数学本科生自我导向学习准备度的因素分析

3.2 数学本科生自我导向学习准备度的现状

数学本科生自我导向学习准备度量表的各项平均得分情况见表2．

表2 数学本科生自我导向学习准备度的描述统计

由表2可知，数学本科生自我导向学习准备度总量表和各因素的平均分都在3~4分之间，说明数学本科生自我导向学习准备度处于中等偏上的水平．对各因素具体描述如下．

3.2.1 终身学习

终身学习因素的平均得分为3.91分，是5个因素中最高的，各题得分在3.64~4.29之间．如第7题“如果我对所学的数学内容感兴趣，我一定会坚持不懈的”4.29分，37题“我非常渴望学习新的数学知识”3.64分，46题“不管我的年龄多大，我都可以学习新的数学知识”4.00分，48题“我喜欢展望未来”3.91分．整体而言，数学本科生对终身学习的认可度较高，终身学习意识较强，能够对新事物持有比较积极、乐观的态度，这将有利于学生适应知识飞速更新的时代，不断完善与发展自己的数学知识和能力．

3.2.2 独立学习

独立学习因素的平均得分为3.47分，各题得分在3.05~3.68之间，均超过了理论中值3．如第10题“任何我需要知道的数学知识，我都能自己去学习”3.36分，18题“我很清楚自己要学习什么”3.45分，25题“我知道自己的学习进度与情形”3.62分，26题“我能对自己的数学学习负责任”3.68分，28题“在学习的时候，我会参与决定自己学什么以及怎样学”3.57分．相对而言，第8题“无论是课堂听讲还是自学，我的数学学习都很有效”在该因素中得分最低，为3.05分，仅有30.91%的学生认为自己的学习有效或比较有效．由上述结果可以看出数学本科生具有一定的独立学习意识和能力，基本上能对自己的学习负责任，但是学习的有效性有待进一步提高．

3.2.3 问题解决

问题解决因素的平均得分为3.05分，是5个因素中最低的，各题得分在2.57~3.35之间，大都在中值附近．如第36题“我能够想到许多不同的方法来解决同一个问题”3.03分，50题“我有能力解决数学难题”3.35分，51题“我擅长提出解决数学问题的新方法”3.03分，55题“我喜欢对困难问题打破沙锅问到底”3.32分，这些说明学生的数学问题解决能力一般，特别是创造性的解决问题的能力比较薄弱．在该因素中，得分最低的为15题“大家一起讨论问题时，我常成为团体的领导者”，仅为2.57分，有54.85%的学生认为自己从未或基本上没有成为团体的领导者，只有17.58%的学生认为自己是领导者，这说明大部分学生不具备高水平的问题解决能力，也缺乏带领、指导和组织团队解决问题的才能，而这些能力不论是在今后的学习还是工作中都是非常重要的，需要引起重视并逐步加以培养．

3.2.4 积极学习

积极学习因素包含的各题项都为反向计分题，均经反向计分处理，因素总体平均得分为3.26分，略高于理论中值，各题得分在2.93~3.66之间．如第5题“我不喜欢别人指出我的错误”3.66分，20题“我的数学学习总是很被动”3.46分，22题“每当遇到困惑的数学问题时，我就避开它”3.35分，29题“如果我的数学学的不好，那也不是我的错”3.34分，49题“我不喜欢学习困难的事情”3.11分，可以看出数学本科生大都能够积极主动地参与学习活动，愿意接受别人的批评或自我评论．但是也有两题的得分低于3分，即第2题“如果一道数学题考试不会考，我就不用去学它”2.93分，说明在平时的学习中还存在一些功利意识和投机思想，这是应该摈弃的；23题“即使我有很好的想法，我却难以去实现它”2.96分，反映出学生想做却做不好，未能取得积极的结果．

3.2.5 热爱学习

热爱学习因素的平均分为3.62分，各题得分在3.25~4.34之间，如第1题“每当我完成数学学习任务时，我就感到很高兴”4.34分，31题“学习数学是一件很有乐趣的事”3.35分，32题“我想学习的东西实在太多，真希望每天有更多的时间可用”3.65分，33题“我喜欢学习数学”3.32分．可以看出，数学本科生大都比较热爱学习，并能够从学习中感受到快乐、享受到乐趣，对学习怀有积极的情感．

3.3 数学本科生自我导向学习准备度的性别差异

对男、女数学本科生在自我导向学习准备度上的差异情况进行t检验，结果见表3．

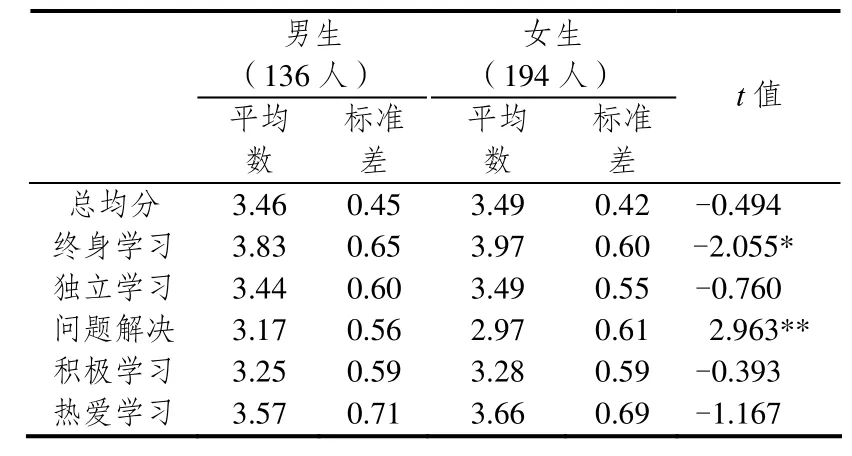
表3 数学本科生自我导向学习准备度的性别差异

由表3可知，数本女生在终身学习方面要显著好于数本男生，而数本男生在问题解决方面要显著好于数本女生．

3.4 数学本科生自我导向学习准备度的年级差异

对4个年级数学本科生在自我导向学习准备度上的差异进行单因素方差分析，结果见表4．

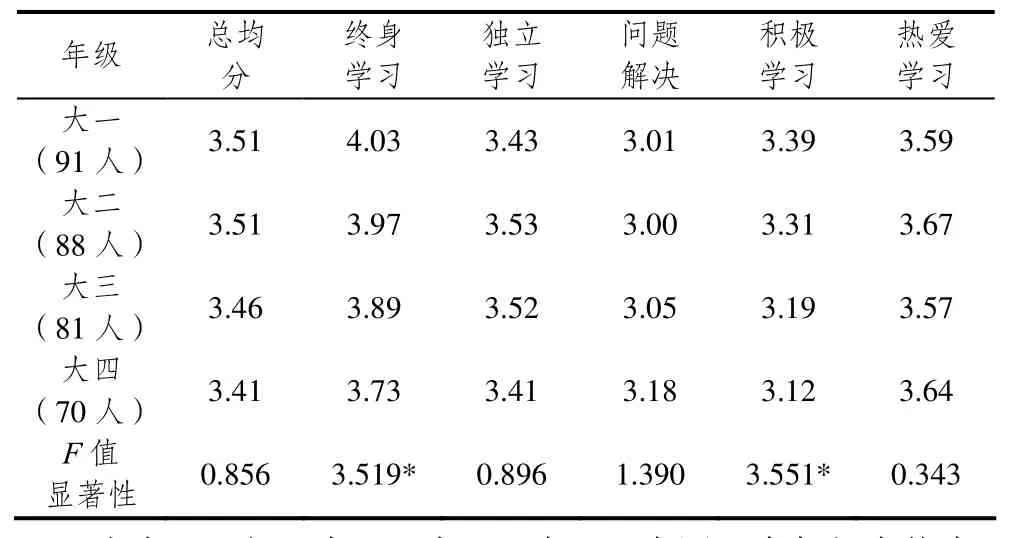
表4 不同年级数学本科生自我导向学习准备度的单因素方差分析

由表4可知，大一、大二、大三、大四4个年级在终身学习和积极学习上存在显著差异．之后的LSD多重比较表明，在终生学习因素上，大一、大二学生得分显著高于大四学生；在积极学习因素上，大一学生得分高于大三、大四学生，大二学生得分显著高于大四学生．

4 分析与讨论

4.1 数学本科生自我导向学习准备度量表的修订情况

研究的修订结果表明，数学本科生自我导向学习准备度量表并未形成Guglielmino版和邓运林修订版的8因素结构，与大陆普通高校大学生的8因素结构和中学生的6因素结构也不同[8，9]，但与大陆的教育硕士生和以护理专业学生为对象修订的自我导向学习准备度量表的5因素结构有不少相似之处[10，11]，这可能是由于自我导向学习准备度具有跨文化差异，也可能是在数学本科生人群上具有独特的结构．从信效度分析的结果来看，数学本科生自我导向学习准备度量表具有良好的信效度，用此量表来检测数学本科生自我导向学习的品质是可靠的．

4.2 数学本科生自我导向学习准备度的性别差异

研究发现，数本女生在终身学习方面要好于男生，而男生在问题解决方面要好于女生．之所以出现这样的性别差异，可能是由于自我导向学习准备度作为学习者的一种意识和能力指标，更多地反映了男女学生的性格倾向以及在长期的数学学习中所形成的对待学习的态度、情感和价值观．女生做事耐心、细致、有毅力，对待学习可以做到持之以恒、坚持不懈，所以女生的终身学习得分高于男生．相比较而言，男生思维较为灵活和开放，喜欢创造，敢于挑战困难问题，解题思路发散，擅长用非常规的方法思考问题，这些都可能导致男生在创造性问题解决方面要好于女生．

4.3 数学本科生自我导向学习准备度的年级差异

研究结果表明，在终生学习因素上，大一、大二学生得分高于大四学生；在积极学习因素上，大一学生得分高于大三、大四学生，大二学生得分高于大四学生．产生这些差异的原因可能是大一数本新生刚入校园时，对大学的学习和生活充满好奇和憧憬，对今后的学习满怀动力和激情．当适应期度过之后，随着年级的增加，学生的课外活动逐渐增多，情感问题的出现，就业危机感的产生，开始逐步困扰着学生，在一定程度上影响了他们的学习．另一方面，由于数学专业各门课程都非常抽象，随着年级的增长学业难度不断增加，课业任务也比其他专业繁重，因此学生会逐渐感受到大学数学学习的单调与枯燥，这些都可能导致数学专业本科生学习的积极性和终身学习数学的意愿随着年级的增加而递减．

5 思考与建议

5.1 加强数学本科生自我导向学习策略的辅导

通过对数学本科生自我导向学习能力现状的调查，发现数学本科生学习有效性水平不高，而要想进行有效的大学数学学习，没有有效的学习策略是不行的．因此，在数学本科生的教学中，应加强自我导向学习策略的辅导，包括制定计划策略、阅读策略和批判性思考策略[6]．针对数学专业学生的制定计划策略，是指能够准确判断自己的学习需要并制定适当的学习目标，选择合适的大学数学学习方法，运用时间管理策略有效利用时间，经常反思自己的学习效果并能及时调整自己的学习目标和学习方法．数学阅读策略包括数学地把握阅读环节，破除语文式阅读习惯，主动思考，力求做出一些个人猜测、估计，养成主动式阅读习惯，并做好阅读笔记[12]．批判性思考策略包括理解数学批判性思考的价值，激励学生积极进行批判性思考，敢于对数学学习内容提出质疑，用新视角重新审视权威和经典，促进元认知训练，指导学生对数学学习过程进行自我监控与反思，不断提高批判性思考的勇气和能力．通过这些策略的传授与指导，使学生养成良好的学习习惯，逐渐实现自我导向学习，提高大学数学学习的效果、效率和效益，提升学习品质．

5.2 注重数学本科生大学适应性教育

研究发现，数学本科生自我导向学习准备度在终生学习因素和积极学习因素上存在显著的年级差异，表现为随着年级的增长，终身学习得分和积极学习得分都逐渐降低．为了改变这种现象，教师在加强学生学习策略辅导的同时，还需要做好数学本科生的大学适应性教育，使学生从入学开始就能够逐步根据环境和学习的需要，努力调整自我，在整个4年的大学学习中保持积极性和主动性．具体措施可以采取“本科生导师培养模式”和开设“数学与应用数学专业导论课”[13，14]等形式，使学生对大学的学习和生活有一个基本了解，增加学生对数学专业的认同感，及早做好大学生涯规划．同时还要告诫学生，数学专业课程都是很抽象的，大学4年的数学学习是有难度的，需要很大的毅力和耐力，要做好持续艰苦学习的心理准备，努力克服学习倦怠和消极情绪，不能中途退缩．适应性教育并不仅仅限于大一，应该贯穿于整个大学数学学习的全过程，以帮助学生不断调整自我，适应大学数学的学习，保持旺盛的精力和学习动力，达到与数学本科学习环境相平衡的状态，最终实现终身学习与持续发展．

5.3 开展各种数学实践活动提高学生创造性解决问题的能力

针对数学本科生问题解决能力一般，特别是创造性解决问题能力较弱的现状，可以通过开展各种数学实践活动的方法来解决．数学实践活动的形式多样，主要包括研究性学习、数学建模、数学实验、学生助教、助研活动等形式[14~17]．研究性学习是创造性思维形成的有效途径，可以提高学生的创新意识和解决问题的能力；学生助教、助研活动可以为学生创造更多的参与教学、科研等工作的机会，提供发挥学生创造性的平台，促进学生创新兴趣和能力的培养；数学建模有助于提高学生的想象力和洞察力，培养学生的直觉思维和发散思维，并有助于提升学生的动手能力和自我评价能力；在数学实验中由于计算机的引入和数学软件包的应用，使学生摆脱了繁重而乏味的数学演算和数值计算，有更多的时间去做创造性工作，有助于培养学生用计算机技术和数学知识解决实际问题的能力．

[1] 杨明升，何晓敏，宁连华．大学数学专业本科生数学学习现状的调查研究[J]．数学教育学报，2010，19（6）：56-59．

[2] 王淑桢．培养大学生自主学习能力 适应终身学习需要[J]．黑龙江高教研究，2004，（4）：148-150．

[3] Tough A M. The Assistance Obtained by Adult Self-teachers [J]. Adult Education, 1966, (17): 30-37.

[4] 高存艳．成人教育哲学流派的自我导向学习观[J]．继续教育研究，2003，（6）：42-44．

[5] Guglielmino L M. Development of the Self-directed Learning Readiness of Adult Scale [D]. Unpublished Thesis. Georgia: Department Education, University of Georgia, 1977.

[6] 张典兵．成人自我导向学习：理念与策略[J]．继续教育研究，2007，（5）：173-175．

[7] 林雨洁．职前教师自我导向学习准备度与国小自然科探究教学实作表现之相关研究[D]．屏东：国立屏东教育大学数理教育研究所，2010．

[8] 王菊兰．中澳大学生自我导向学习能力之比较[J]．比较教育研究，2008，（7）：66-70．

[9] 黄水，陈文锋，傅小兰．中学生自我导向学习准备度量表的结构和效度[J]．心理科学，2007，30（1）：148-150．

[10] 张宏，徐富明，安连义．中小学教师在职攻读教育硕士专业学位的自我导向学习的调查研究[J]．教育学报，2006，2（1）：84-90．

[11] 李彦章，杨曦，李敏．自我导向学习量表信度和效度的检测及试用[J]．护理研究，2008，22（4）：930-932．

[12] 厉小康．数学阅读能力的培养研究[J]．数学教育学报，2004，13（2）：89-92．

[13] 喻华杰，宁连华．大学数学本科人才培养教学特区的实践与探索[J]．数学教育学报，2011，20（3）：93-96．

[14] 陈秀，张霞，牛欣．应用型本科高校数学与应用数学专业建设的探索与实践[J]．大学数学，2012，28（1）：5-9．

[15] 李三平，李传峰．研究性学习在中学数学教学中的体现与应用探析[J]．数学教育学报，2004，13（3）：76-78．

[16] 付军，朱宏，王宪昌．在数学建模教学中培养学生创新能力的实践与思考[J]．数学教育学报，2007，16（4）：93-95．

[17] 张晓磊，郭华光．试论数学实验的数学教育功能[J]．数学教育学报，2003，12（2）：38-41．

附录——数学专业本科生自我导向学习倾向性量表（施测使用）

同学们，感谢您抽出宝贵的时间，协助我们完成此次问卷调查．本问卷只作为科学研究之用，并不是评价您学习的好坏，答案之间也无对错之分，请放心答题！

年级：_____性别：_____

下面是您在学习时可能出现的一些做法或想法，请您根据自己的实际情况从A、B、C、D、E五个选项中选择一个适合自己的答案．如果某句话的内容完全符合您的情况，您就选A；如果比较符合您的情况，您就选B；以此类推．通常看到问题后第一次呈现在您脑海中的答案，一般而言是最贴切的，请真实地填写您的个人情形，我们对您的合作表示最真诚的致谢！

A.完全符合 B.比较符合 C.有点符合 D.基本不符合 E.完全不符合

1、每当我完成数学学习任务时，我就感到很高兴．( )

2、如果一道数学题考试不会考，我就不用去学它．( )

3、我对学习数学的兴趣不像别人那么大．( )

4、我认为看数学书是枯燥无味的．( )

5、我不喜欢别人指出我的错误．( )

6、我喜欢与别人交流思想探讨问题．( )

7、如果我对所学的数学内容感兴趣，我一定会坚持不懈的．( )

8、无论是课堂听讲还是自学，我的数学学习都很有效．( )

9、只要我决定学习，不论多忙，我都会抽空去学．( )

10、任何我需要知道的数学知识，我都能自己去学习．( )

11、我知道从哪里去获得数学学习资料．( )

12、我会去做自己认为应该做的事情．( )

13、我知道该在什么时候、在什么学习内容上花更多功夫．( )

14、使用我认为有效的学习方法，比尝试新的方法更好．( )

15、大家一起讨论问题时，我常成为团体的领导者．( )

16、我比一般人更能发现我需要学习的东西．( )

17、我希望老师在上课时，都能明白地告诉大家应该做什么．( )

18、我很清楚自己要学习什么．( )

19、当我想要探讨某些事情的时候，我就会去做．( )

20、我的数学学习总是很被动．( )

21、我常常看不懂书上写些什么．( )

22、每当遇到困惑的数学问题时，我就避开它．( )

23、即使我有很好的想法，我却难以去实现它．( )

24、我在学习数学时不为困难的问题所阻挡．( )

25、我知道自己的学习进度与情形．( )

26、我能对自己的数学学习负责任．( )

27、只要是我想学的东西，我总能找到合适的方法来学习它．( )

28、在学习的时候，我会参与决定自己学什么以及怎样学．( )

29、如果我的数学学的不好，那也不是我的错．( )

30、我最赞赏那些好学不倦的人．( )

31、学习数学是一件很有乐趣的事．( )

32、我想学习的东西实在太多，真希望每天有更多的时间可用．( )

33、我喜欢学习数学．( )

34、我经常想要学习．( )

35、整天不停地学习令人厌烦．( )

36、我能够想到许多不同的方法来解决同一个问题．( )

37、我非常渴望学习新的数学知识．( )

38、即使不能肯定结果会如何，我仍然喜欢尝试新事物．( )

39、我不喜欢思考没有正确答案的东西．( )

40、我对很多事物都充满好奇心．( )

41、我擅长用异于常规的方法解决数学问题．( )

42、每年我都要自行学习许多东西．( )

43、我想学习更多的知识，使自己不断成长．( )

44、我学的越多，就觉得世界越精彩．( )

45、只有不断学习的人才能成为领导者，因为他的知识与时俱进．( )

46、不管我的年龄多大，我都可以学习新的数学知识．( )

47、我乐意活到老、学到老．( )

48、我喜欢展望未来．( )

49、我不喜欢学习困难的事情．( )

50、我有能力解决数学难题．( )

51、我擅长提出解决数学问题的新方法．( )

52、对我而言掌握数学学习方法是十分重要的．( )

53、我很容易掌握基本的数学学习技巧．( )

54、我尝试将所学的知识与自己的计划联系起来．( )

55、我喜欢对困难问题打破沙锅问到底．( )

[责任编校：周学智]

Investigation and Analysis on Self-directed Learning Ability of Mathematics-major Undergraduates

DING Ya-yuan1, WANG Min2, CHEN Ke-sheng3

(1. Education Science College, Anhui Radio & TV University, Anhui Hefei 230022, China; 2. Mathematics Science College, Anhui University, Anhui Hefei 230601, China; 3. Department of Computer and Mathematics, Anhui Normal University, Anhui Wuhu 241000, China)

Investigated mathematics undergraduates’ self-directed learning situation through revising the self-directed learning reading scale. The results showed that: Mathematics undergraduates’ self-directed learning reading scale had 5 factors of structure, the scale had good reliability and validity; mathematics undergraduates’ self-directed learning reading was in the mid to upper level; there were gender, grade differences in different factors. In mathematics teaching, we should strengthen mathematics undergraduate’ self-directed learning strategies training; pay attention to mathematics undergraduate’ adaptability education; launch the practice of mathematics, improve students’ ability to solve problems creatively.

mathematics major; undergraduate; self-directed learning; investigation; analysis

G420

：A

：1004–9894（2014）01–0051–06

2013–10–05

2012年度安徽省教育科学规划课题——高中数学课程中数学文化及其典型案例研究（JG12016）；安徽电大青年教师科研基金项目——远程学习者在线学习力研究（qn13-18）

丁亚元（1981—），女，安徽合肥人，讲师，硕士，主要从事数学教学论和远程开放教育研究．