实货制下铁路枢纽货运站业务调整模型

刘勇，朱晓宁

（北京交通大学交通运输学院，北京 100044）

*交通运输专栏*

实货制下铁路枢纽货运站业务调整模型

刘勇，朱晓宁

（北京交通大学交通运输学院，北京 100044）

根据实货制铁路货运的基本要求，对铁路枢纽货运站进行业务调整优化。首先，明确铁路决策部门与货运客户之间的主从决策关系，建立铁路枢纽内货运站业务调整双层规划模型。上层模型以最小化枢纽货物周转量和业务分散度为目标，下层模型以客户集运成本最小化为目标。接着通过构造上、下层决策变量间的反应函数，设计了求解模型的启发式算法。最后，采用算例对模型和算法进行可行性验证。结果显示，调整后货运站业务分散度降低72.5%，枢纽货物周转量降低40.2%，而客户运输费用只增加8.4%。

铁路货物运输；枢纽货运站；业务调整；双层规划；启发式算法

铁路总公司于2013年实行“实货制”改革，借助网络平台，通过对托运货物的“身份验证”，简化货主托运手续来保障货运业务办理方式的网络化、信息化，在一定程度上改善了货运环境。现阶段，虽然货主能及时要到车皮，并将货物装车，但由于货运业务分散且相互重叠，使货物在类别、性质上不统一进而造成车流无法满足编组开行条件，使得货物在货运站滞积。因此，有必要优化枢纽内既有货运站的业务布局和功能定位，缩减中转集结时间。

目前国内外对铁路枢纽货运组织的优化研究多从车流组织［1］和编组计划［2］两方面进行，且取得了丰硕的成果，对货运站点的优化研究主要集中在货运集中化［3］和货运站空间布局方面［4］，而对枢纽货运站业务的分工研究多以定性分析［5－6］和布局优化［7］为主，定量化研究多见于对枢纽客运站的业务调整［8－9］，缺乏对既有货运站的货运业务类别分工进行深入的定量化研究。

本文考虑货物从货源地装车到货运站装车的运输作业过程，运用定量分析的方法对铁路枢纽内货运站各站点业务进行重新调整，完善货运站业务布局分工和功能定位，将车流集结转变为货流集结，缩短货物在车站的集结、中转时间，提高运输组织效率。

1 业务调整双层规划模型

1.1 模型建立思路

本文采用双层规划思路建立基于货主和铁路部门的数学规划模型。其中上层模型以铁路部门为中心，实现枢纽区域短途集疏运成本最低；下层模型以货主为中心，实现个体货运成本的最小化。

货运站业务调整的实质是实现货运站业务集约化和专业化分工，基于此，文中引入货运业务分散度和作业相似度概念。货运业务分散度指的是铁路枢纽内各种货运业务的分散程度，以枢纽内各货运站所承担货运业务种类之和表示，业务分散度越小，表示货运站货运业务办理集中程度越高。作业相似度指的是不同货物种类之间最佳作业设备及作业性质之间的契合程度，作用有二：一是作为货运站专业化过程的约束条件，二是表征因作业性质不契合而产生的额外转运装卸成本。作业相似度越高，越能提高货运站作业设备的利用率，提高货运站作业效率。因此，上层规划模型的一个目标为最小化枢纽内业务分散度，此外，将作业相似度作为业务调整的一个约束条件考虑在内。

1.2 模型参数定义

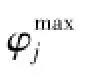
xjk为上层模型决策变量，若货运站j办理品类k的货运业务，则有xjk＝1，否则xjk＝0；yijk为下层模型决策变量。

1.3 上层规划模型

枢纽货运站业务调整以货运站空间布局优化为前提，满足以下几点假设：

（1）货运站位置确定，且其间距离已知；

（2）客户货源地可到达枢纽内任意货运站；

（3）枢纽内货运站作业能力、作业设备性质固定且已知；

铁路的公共服务属性决定了在注重企业本身运营效益的同时还要考虑社会效益，就业务调整而言，一是要确定货运站开展的货运作业种类；二是要合理调配各个货运站的业务类型，使其既满足区域货运需求，又能减少对枢纽内公路交通的影响，降低枢纽内短途公路集疏运成本，这是第一目标。在一定时期内，公路运输费率是一定的，因此可以用公路运输货物周转量来代替枢纽内短途公路运输成本。此外，为提高枢纽内货运业务的集中化水平，另一目标是降低枢纽业务分散度。本文用权重系数法将多目标转化为单目标。上层目标函数为

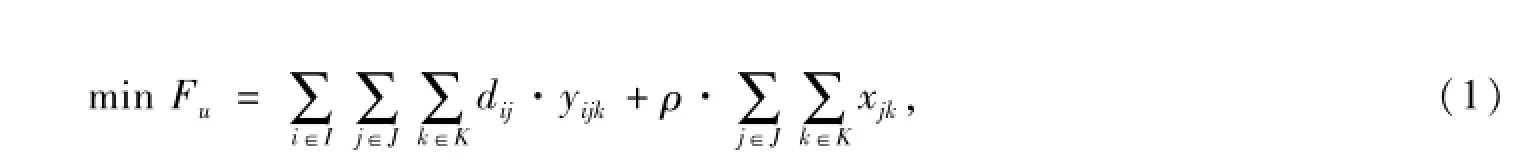
枢纽货运站业务调整过程主要受到货运站作业能力、业务分布空间距离以及作业相似度等约束。

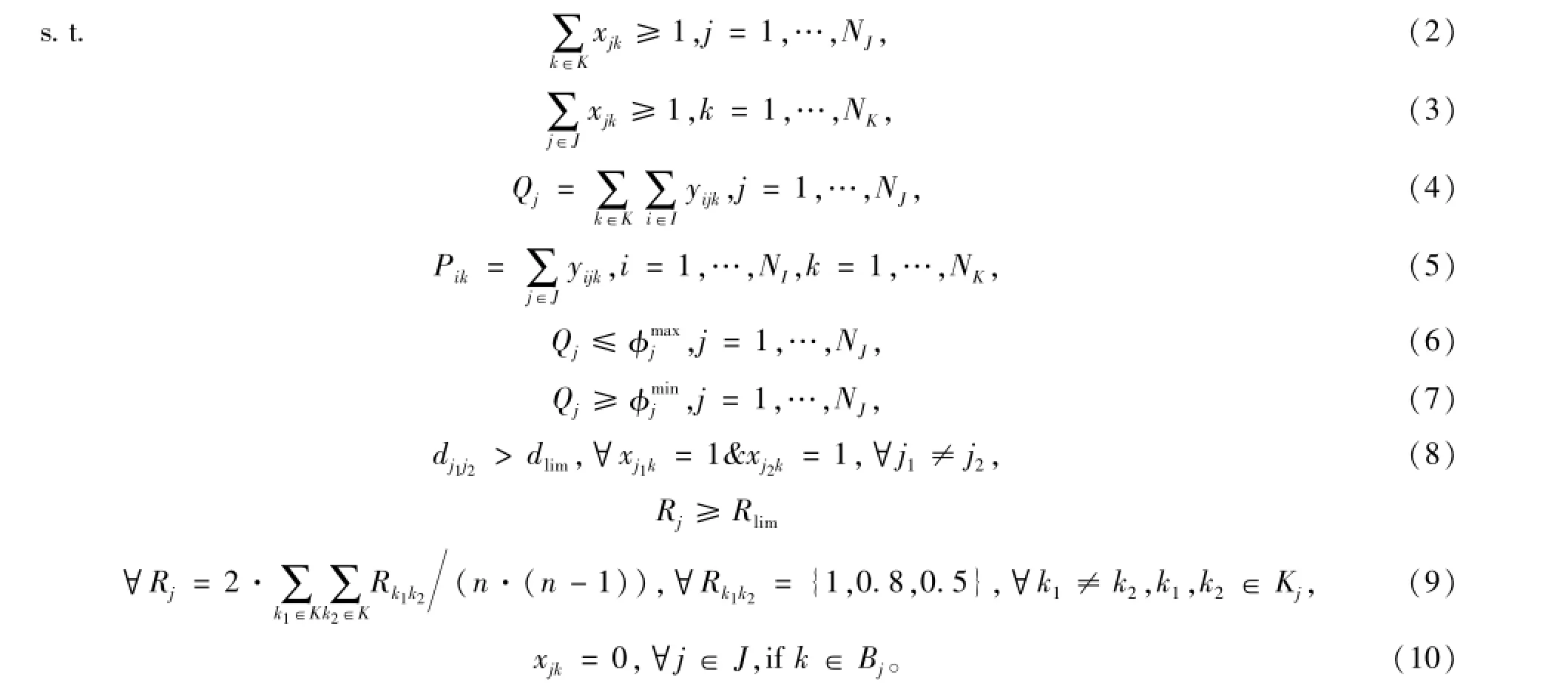
其中，式（2）为货运站业务种类约束；式（3）体现枢纽内货物品类的全覆盖，即枢纽内每个货物品类的业务至少有一个货运站承担；式（4）表示货运站j承担的货运量；式（5）表示客户i产生的货类k的运输需求量，由枢纽内货运站共同承担；式（6）、（7）为货运站j的货运量约束，既不能超出货运站作业能力，也不能少于保持货运站存在的最少货运量；式（8）表示办理同一种货物品类的货运站之间的距离约束，要求办理同一货类业务的货运站之间的距离不能太近；式（9）为货运站办理的货类业务之间的作业相似度约束，不能少于货运站的最低作业相似度；式（10）表示货运站的限制货类作业约束。

1.4 下层规划模型

客户作为参与运输过程的独立个体，总是从自身利益角度做出对其最有利的决策，因此，在下层模型中假定：

（1）客户总是优先选择距离货源地距离最近的货运站运输；

（2）客户运输计划根据货运站业务调整方案及时调整；

（3）客户同批次同类别货物可以选择不同货运站服务；

同时，客户作为运输过程的发起者，主要考虑运输成本和途中作业成本，下层规划模型以实现公路运输费用和转运装卸费用最小化为目标。模型为

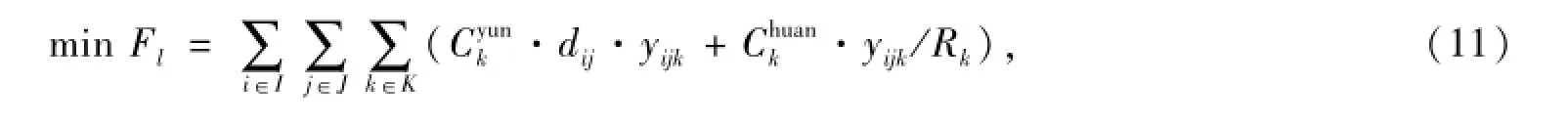
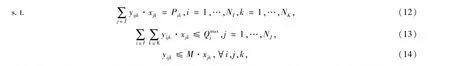
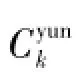
2 算法求解

双层规划问题是一种非凸非光滑的优化问题，即使是线性双层规划问题也已被证明为NP-hard问题，因此，可采用启发式算法对模型进行求解。目前，国内外求解双层规划的方法有Kuhn-Tucker方法、罚函数法以及反应函数法等［10］。本文采用的是反应函数法［11］，通过建立上、下层模型之间的约束关系对模型进行反复求解从而得到模型的近似最优解。分析模型可知，上层模型中业务布局方案xjk以下层模型反馈的货运量yijk分配结果为调整依据，而下层模型的货运量分配是以各个货运站的业务分工为前提的，式（14）反映了在既有货运站空间布局的前提下，枢纽货运站的业务布局方案xjk与货运站货运量yijk之间的相互耦合关系。对下层规划问题而言，xjk（0，1）是已知的，若xjk＝1，那么yijk≤M，由于M为一足够大正整数，此时约束（14）自然成立；若xjk＝0，则yijk＝0，此时约束（14）也成立，可以看出，在上层规划中xjk确定后，下层规划约束（14）可以去掉。为了构造反应函数的具体形式，引入松弛变量γijk（γijk≥0），则式（14）转化为

给定决策变量xjk的一组解，可以利用单纯性法求得下层模型中的yijk，利用式（15）得到松弛变量γijk，记为γ′ijk，即得到γijk对xjk的反应函数为

将式（16）代入上层模型目标函数式（1）中，则上层规划问题可转化为混合整数规划问题，可用分支定界法进行求解，得到上层最优解后将其代入下层规划模型，求出下层最优解，重复以上思路，直至求得双层规划模型的最优解或近似解。具体算法步骤如下。

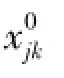
此算法虽然无法严格证明其收敛性，在实际操作中可通过多次取不同初值进行试算，若每次结果相近，可说明算法对于本规划模型是收敛的。

3 算例分析

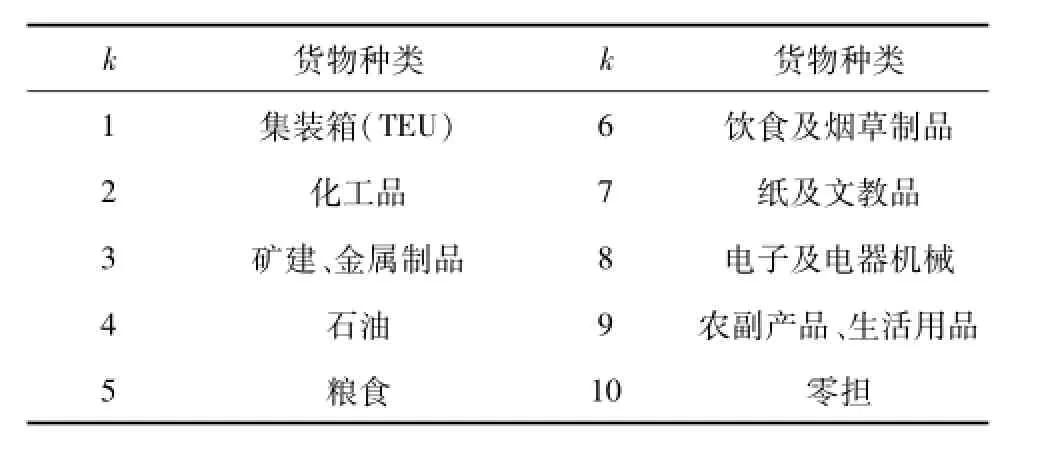
表1 货物分类表Table 1 Classification table of goods

3.1 算例描述

选取某城市铁路枢纽对模型和算法的可行性、有效性进行验证。根据枢纽范围内交通运输实际情况，按照货运量大小以及地理位置对客户进行归并，最后确定参与计算的客户有7家，枢纽内参与业务调整的货运站为4个，参与调整的货物有10类。货物分类表如表1所示，表2是枢纽一年内客户对各品类货物的运输需求量，表3为枢纽客户到货运站的距离以及货运站之间的距离。公路运输运价率以及铁路装卸费率根据《铁路货物装卸作业计费办法（2005）》相关规定和汽车货物运输规则查定，如表4所示。根据实践情况和模型求解结果，ρ＝（0.7×107）／（0.3×102）。

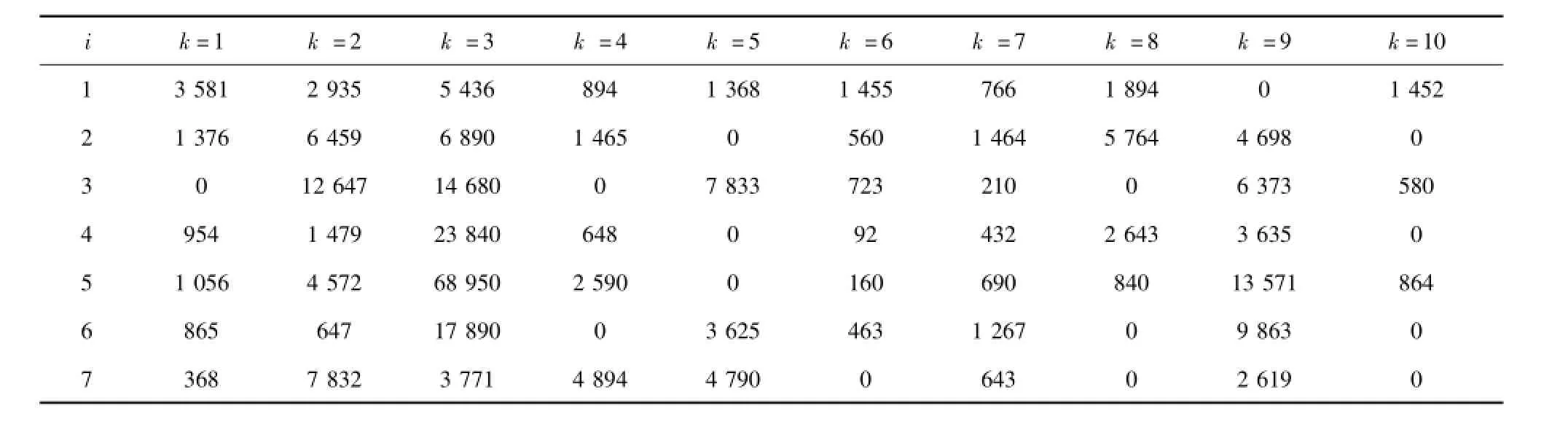
表2 客户对各品类货物的运输需求量PikTable 2 Freight volume demand of all goods categories of freight clients

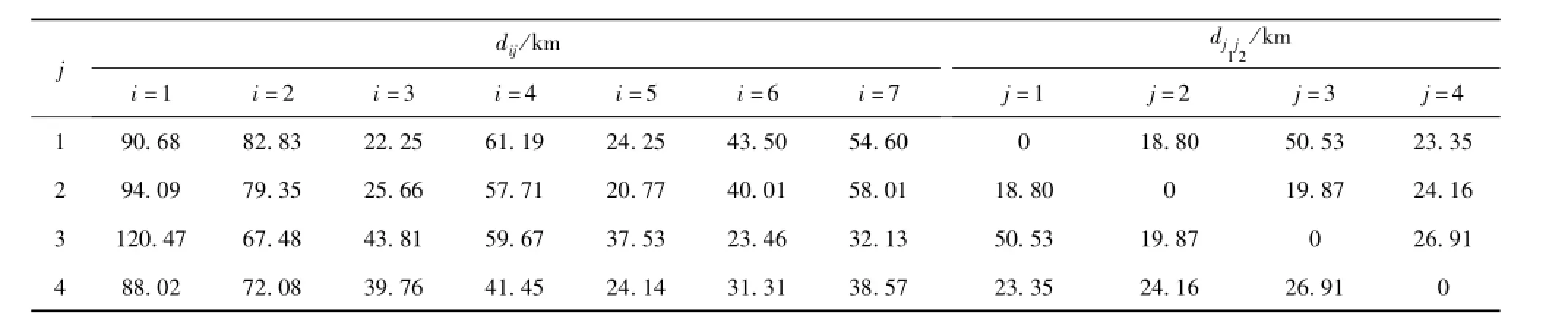
表3 枢纽内客户到货运站的距离dij和货运站之间的距离dj1j2Table 3 Distance of clients to stations andstations to stations in a freighthub

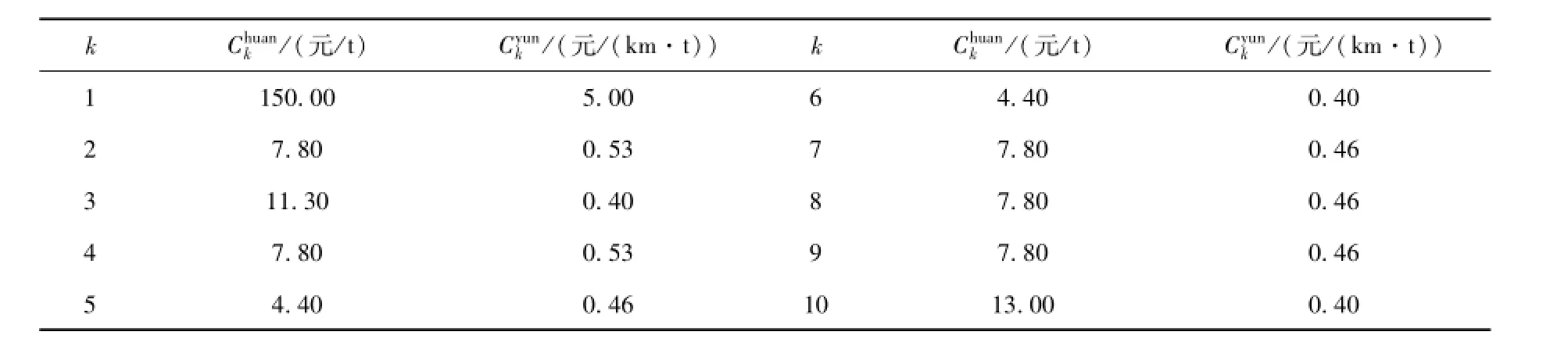
表4 各类货物中转装卸费率以及公路运输运价率Table 4 Unit fare of transfer androadtransportation of all kinds of goods

根据货物性质以及枢纽内货运站的作业性质特点，将各类货物分为三大类，定义集合A，B，C，已知有A＝｛5，6，7，8，9，10｝，B＝｛1，3｝，C＝｛2，4｝，对于货类k1，k2，（1）若k1，k2∈A｜B｜C，则有Rk1k2＝1；（2）若k1∈A＆k2∈B，则有Rk1k2＝0．8；（3）若k1∈A｜B＆k2∈C，则有Rk1k2＝0．5。根据枢纽内物流发展规划和货运站专业化作业要求，规定调整后的货运站作业相似度不能小于Rlim＝0.7。

3.2 计算结果及分析

3.2.1 初始方案

表5 初始货运量分配方案Table 5 Initial distribution scheme of freight vol，

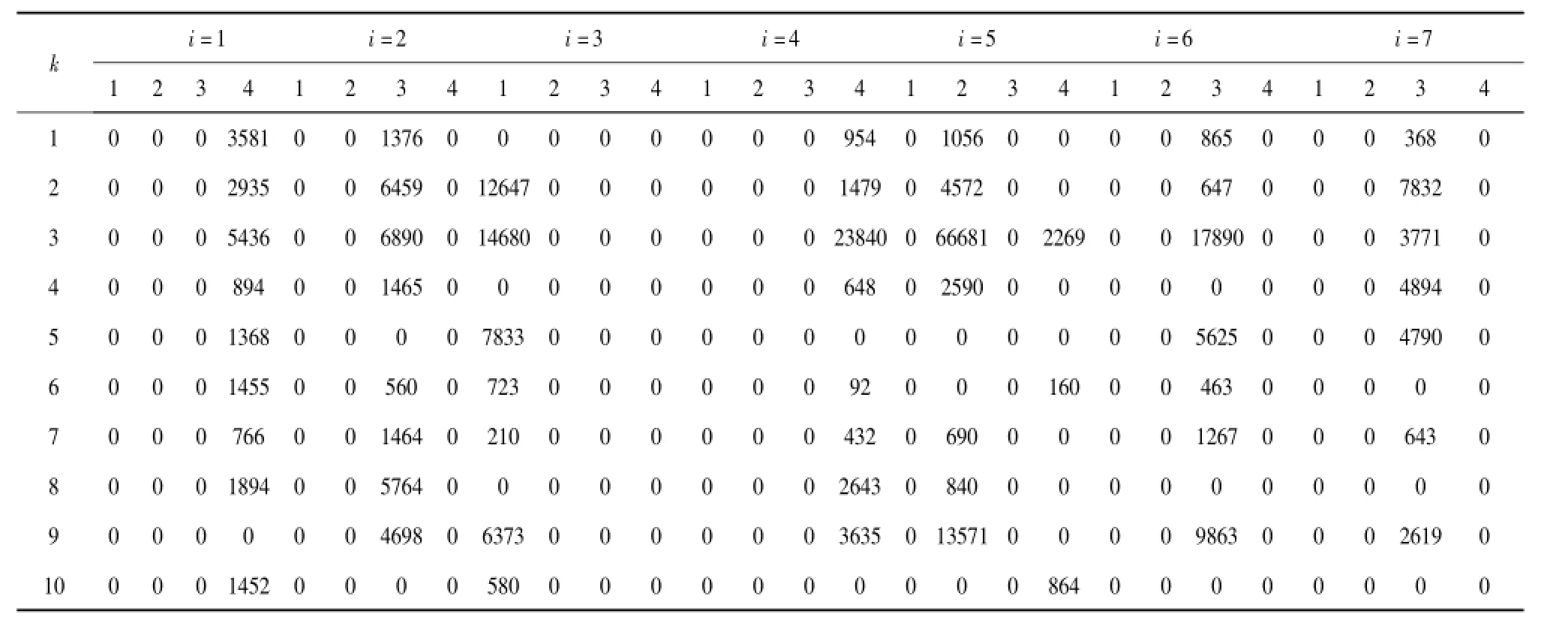
表5 初始货运量分配方案Table 5 Initial distribution scheme of freight vol，

i＝1 i＝2 i＝3 i＝4 i＝5 i＝6 i＝7 k 1 2 3 4 1 2 3 4 1 2 3 4 1 2 3 4 1 2 3 4 1 2 3 4 1 2 3 4 1 0 0 0 3581 0 0 1376 0 0 0 0 0 0 0 0 954 0 1056 0 0 0 0 865 0 0 0 368 0 2 0 0 0 2935 0 0 6459 0 12647 0 0 0 0 0 0 1479 0 4572 0 0 0 0 647 0 0 0 7832 0 3 0 0 0 5436 0 0 6890 0 14680 0 0 0 0 0 0 23840 0 66681 0 2269 0 0 17890 0 0 0 3771 0 4 0 0 0 894 0 0 1465 0 0 0 0 0 0 0 0 648 0 2590 0 0 0 0 0 0 0 0 4894 0 5 0 0 0 1368 0 0 0 0 7833 0 0 0 0 0 0 0 0 0 0 0 0 0 5625 0 0 0 4790 0 6 0 0 0 1455 0 0 560 0 723 0 0 0 0 0 0 92 0 0 0 160 0 0 463 0 0 0 0 0 7 0 0 0 766 0 0 1464 0 210 0 0 0 0 0 0 432 0 690 0 0 0 0 1267 0 0 0 643 0 8 0 0 0 1894 0 0 5764 0 0 0 0 0 0 0 0 2643 0 840 0 0 0 0 0 0 0 0 0 0 9 0 0 0 0 0 0 4698 0 6373 0 0 0 0 0 0 3635 0 13571 0 0 0 0 9863 0 0 0 2619 0 10 0 0 0 1452 0 0 0 0 580 0 0 0 0 0 0 0 0 0 0 864 0 0 0 0 0 0 0 0

初始方案中业务分散度为40，上层规划模型目标函数值为41 947 440 km·t，下层规划模型目标函数值为10 345 120元。

3.2.2 优化方案

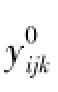
表6 货运站业务调整方案xjkTable 6 Optimizedbusiness scheme in a freight hub

表7 货运量优化分配方案Table 7 Optimized distribution scheme of freight volume

表7 货运量优化分配方案Table 7 Optimized distribution scheme of freight volume

i＝1 i＝2 i＝3 i＝4 i＝5 i＝6 i＝7 k 1 2 3 4 1 2 3 4 1 2 3 4 1 2 3 4 1 2 3 4 1 2 3 4 1 2 3 4 1 0 0 0 3581 0 0 0 1376 0 0 0 0 0 0 0 954 0 0 0 1056 0 0 0 865 0 0 0 368 2 0 2935 0 0 0 6459 0 0 0 12647 0 0 0 1479 0 0 0 4572 0 0 0 647 0 0 0 7832 0 0 3 0 0 0 5436 0 0 0 689014680 0 0 0 0 0 0 23840 44977 0 0 23973 0 0 0 17890 0 0 0 3771

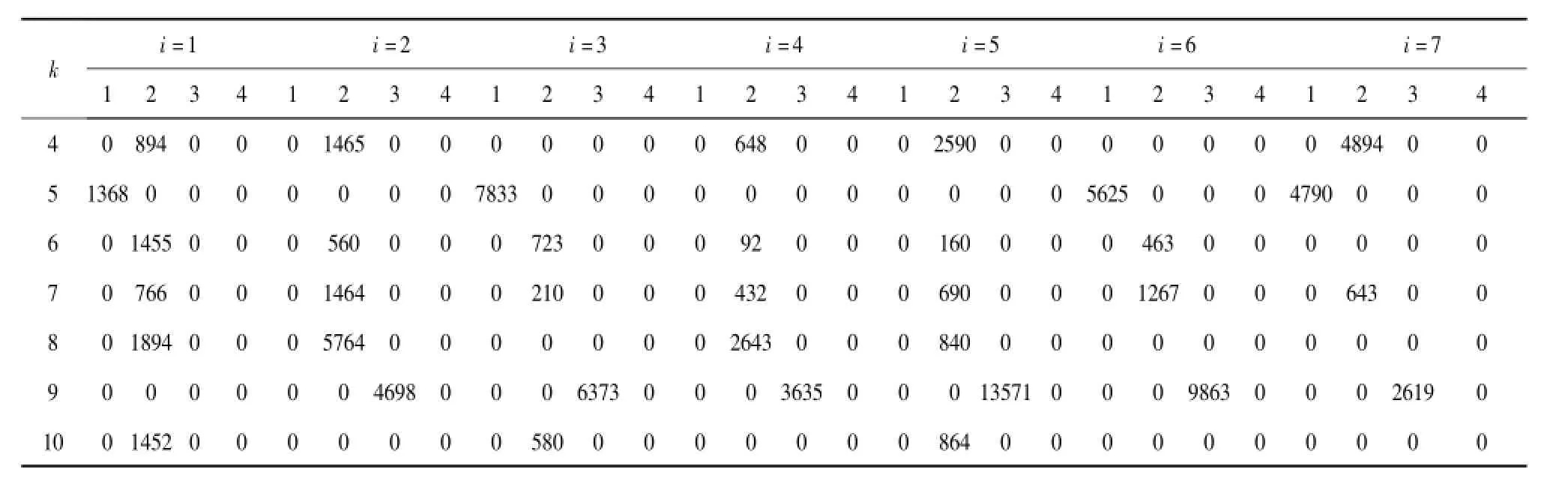
续表7

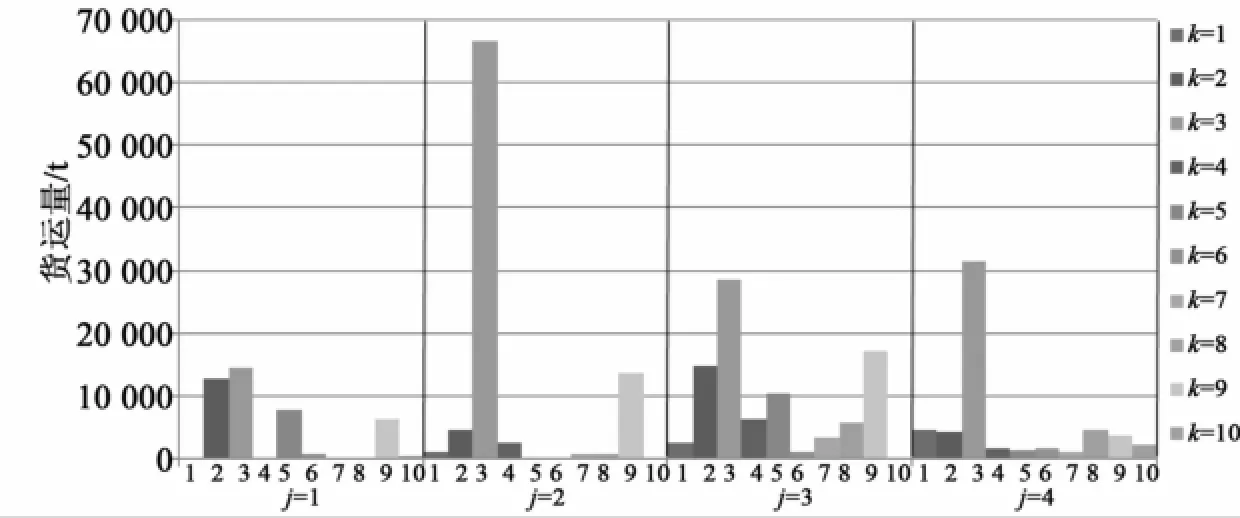
图1 初始方案货运站j承担货类k的货运量Fig.1 Freight volume of goods category of freight station of the initial scheme

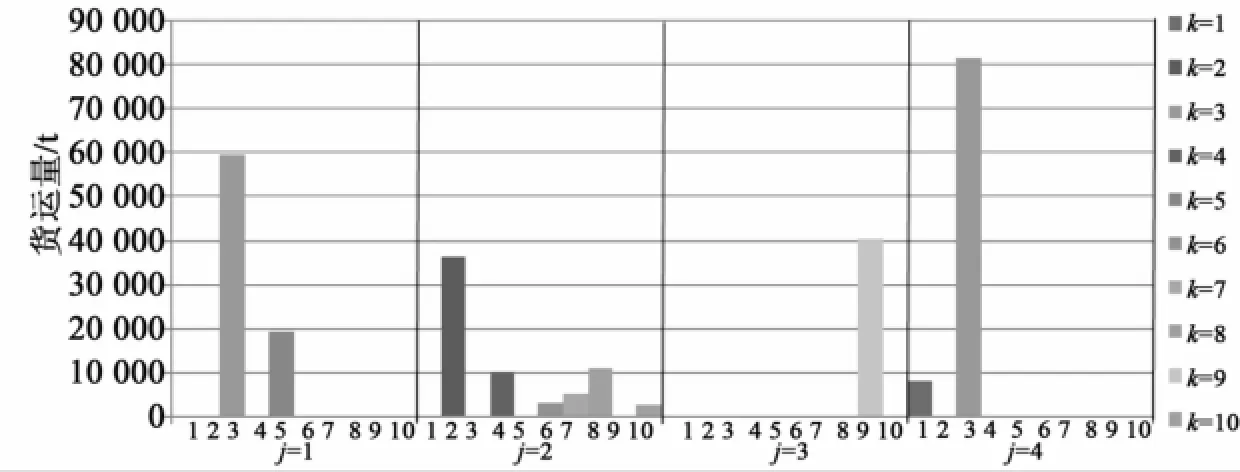
图2 优化方案货运站j承担货类k的货运量Fig.2 Freight volume of goods category of freight station of the optimal scheme

由表6可知，优化后业务分散度为11，调整后的货运站均满足作业相似度要求，上层规划模型目标函数值为25 076 720 km·t，下层规划模型目标函数值为11 297 020元。

对比优化调整前后结果，优化方案比初始方案业务分散度降低72.5%，枢纽内货运站作业集约化、专业化程度大为提高；枢纽内货物周转量的减少带来铁路运输费用的减少，达40.2%；货主总运输费用（公路运输和转运装卸）增加8.4%。总的来说运输费用是减少的，由此可知，文中提出的业务调整方案是优化的。此外，由图1、2可知，业务调整前，枢纽内所有货运站均为综合货运站；调整后，货流流向更为集中，货运站1、3、4调整为专业货运站，货运站2仍为综合货运站，但办理的业务种类由7类调整为6类。具体为：货类3业务调整为只由货运站1和4办理，货类5全部在货运站1办理，货类1只由货运站4办理，货运站2办理货类2、4、6、7、8、10的全部货运作业，货运站3只办理货类9的货运业务。

以上调整方案是基于一定时期内枢纽区域历史货运量分析的结果，而货运量是动态且不断发展的，因此，所提出的调整方案只是一个初步的调整结果，但为将来集约化和专业化的推进提供了有利的前提条件。随着枢纽内货运站业务专业化程度的提高，将会进一步加快枢纽货流流向的集中，反过来又促进货运站的专业化改革。

4 结语

枢纽货运站业务调整为保障实货制的顺利开展提供了一种新的解决思路。引入业务分散度和作业相似度概念，对货运站集约化、专业化进行定量描述，同时作为业务调整的约束条件，实现了货运站作业成本的差异性表征。建立了基于铁路部门和货运客户之间的主从决策双层规划模型，并运用反应函数设计了启发式算法对模型进行求解，确定调整后的货运站业务方案。算例验证了模型和算法的有效性、可行性，优化后的货运站集约化、专业化程度得到提升。今后进一步的研究方向为实现货运站业务分工调整与车流组织协同优化，以及对因运输时间减少而产生的经济效益的定量化描述，构建基于全程物流模式下的货运站业务调整模型。

［1］LIN BL，WANG ZM，JI LJ，et al.Optimizing the freight train connection service network of a large-scale rail system［J］. Transportation Research Part B：Methodological，2012，46（5）：649－667.

［2］黎浩东，何世伟，宋瑞，等.列车编组计划和技术站布局的综合优化［J］.北京交通大学学报，2010，34（6）：30－34.

［3］JEONG S J，LEE C G，BOOKBINDER JH.The European freight railway systemas a hub-and-spoke network［J］.Transportation Research Part A：Policy and Practice，2007，41（6）：523－536.

［4］SPYCHALSKI JC，SWAN P F.US rail freight performance under downsized regulation［J］.Utilities Policy，2004，12（3）：165－179.

［5］王浩.北京铁路枢纽主要客运站分工研究［J］.铁道标准设计，2012（3）：20－23.

［6］陈富强.太原铁路枢纽客运系统分工及布局研究［J］.铁道标准设计，2012（6）：32－35.

［7］徐瑞华，杜世敏，陈百磊.城市铁路枢纽布局的调整优化研究［J］.同济大学学报：自然科学版，2005，33（5）：631－635.

［8］毛保华.枢纽地区铁路客运站布局与分工优化［J］.铁道学报，1992，14（1）：47－55.

［9］赵军，李愈，任其亮，等.铁路枢纽内客运站分工的优化模型及算法［J］.西南交通大学学报，2011，46（1）：148－153.

［10］钟磊钢，李云岗，张翠华.基于价格弹性的双层规划二级分销网络模型［J］.计算机集成制造系统，2006，12（10）：1596－1599.

［11］孙会君，高自友.考虑路线安排的物流配送中心选址双层规划模型及求解算法［J］.中国公路学报，2003，16（2）：115－119.

Goods real name based business reorganization model for railway freight hub

LIU Yong，ZHU Xiao-ning
（School of Traffic and Transportation，Beijing Jiaotong University，Beijing 100044，China）

We optimize business reorganization for railway freighthub basedon the basic requirement of goods realname system．We initially determine the subordinate hierarchical decision-making relationship between railway decision-making departments and its c lients，and then constructa bi-levelp rogramming model for business reorganization of railway freight hub．The ob jec tive of the upper model is to minimize the total freight turnover volume andbusiness dispersion rate in a freight hub．The goalof the lowermodel is to minimize c lient freight cost．We then devise a heuristic algorithmto solve the modelby construc ting a reaction func tion between the upper and the lower decision variab les．We eventually design an example to verify the feasibility of themodelandthe algorithm．Results show thatbusiness dispersion rate of a reorganizedfreight station dec reases by 72．5%，and 40．2%for freight turnover volume，but client freight costonly inc reases by 8．4%．

railway freight transportation；railway freight hub；business reorganization；bi-level programming；heuristic algorithm

U294.1

A

1002-4026（2014）05-0046-08

10.3976／j.issn.1002－4026.2014.05.009

2014-05-08

国家自然科学基金重大项目（71390332）；高等学校博士学科点专项科研基金项目（20130009110001）

刘勇（1990－），男，硕士研究生，研究方向为交通运输规划与管理。Email：13120875＠bjtu.edu.cn