应用EDM法和ACA算法快速计算电大开缝导体RCS

姚雨帆， 孙玉发， 王仲根， 盛 涛

（安徽大学 电子信息工程学院，安徽 合肥 230039）

在目标电磁散射特性的常规分析中，缝隙作为弱散射源，往往被学者们忽视。但随着隐身技术的发展，缝隙对雷达散射截面（RCS）的影响愈加明显［1］。近年来，与计算规则目标RCS相比，研究人员更侧重于对开缝导体电磁散射特性的研究。对于缝隙形状比较简单的目标，当宽度远远小于照射平面波波长时，文献［2］根据Babinet原理推导出较精确的经验公式。对于内部结构复杂且带有电小尺寸缝隙的电大物体，可以采用时域有限差分法［3］、多层快速多极子算法［4］等电磁场数值计算方法，也可以运用各种数值解法与高频近似法相结合的混合算法求解，保证计算的精度和速度，比如物理光学法与矩量法（MOM）结合［5］、周期矩量法与矩量法结合［6］等。此外，文献［7－8］分别介绍了实验测试法和半实测法处理缝隙电磁散射问题，都取得了不错的效果。本文采用等效偶极子（EDM）法加速阻抗矩阵元素填充，并与自适应交叉近似（ACA）算法相结合压缩远场的阻抗矩阵，最终实现电大开缝导体目标RCS的快速计算。

1 理论分析

1.1 等效偶极子法

任意三维理想导体目标在入射平面波Ei照射下，表面S将产生等效电流J，进而产生散射场Es。根据理想导体表面总切向电场为0的边界条件，可得如下方程：

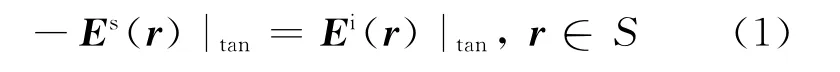
等效电流J可用RWG矢量基函数展开，即

采用伽略金法，权函数选取fm（r），可将（1）式转化为矩阵方程［9］：

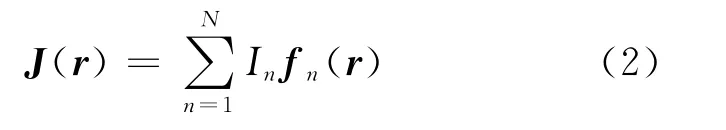
其中，Z为阻抗矩阵；I为待求电流；V为激励矢量。

MoM填充Z的方法如文献［10］所述，计算过程中会涉及大量的双重积分，当未知数较多时，该方法非常耗时。文献［11］提出一种快速填充阻抗矩阵元素的新方法——等效偶极子法。如图1所示，ln、lm分别代表2个三角单元对T±n、T±m的公共边，当场源之间的距离大于某一阈值时，每个三角单元对可等效为一个电偶极子，第n个三角单元对的等效偶极矩表达式如下：

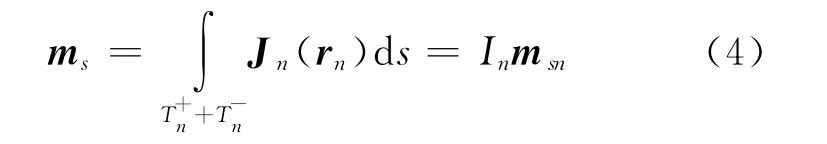
其中，In为电流系数；分别为三角形T＋n、T－n质心的位置矢量。第n个等效偶极子在rn处产生的散射电场［12］可表示为：

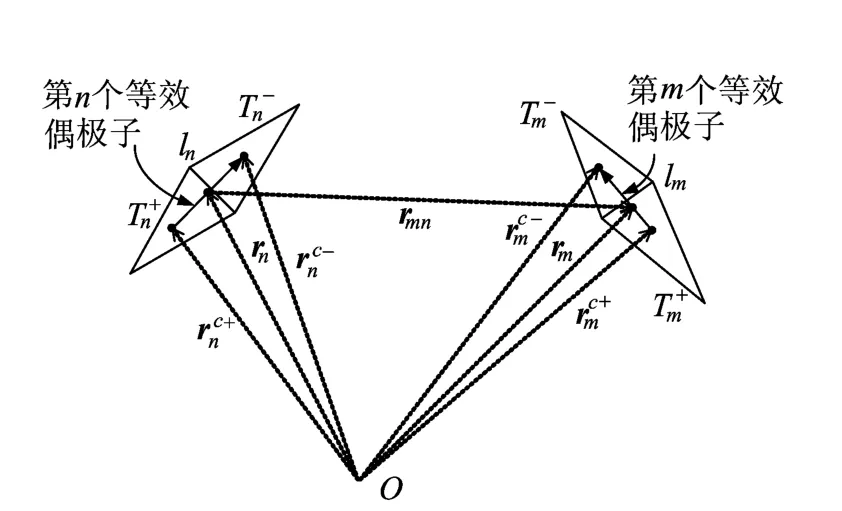
图1 偶极子模型

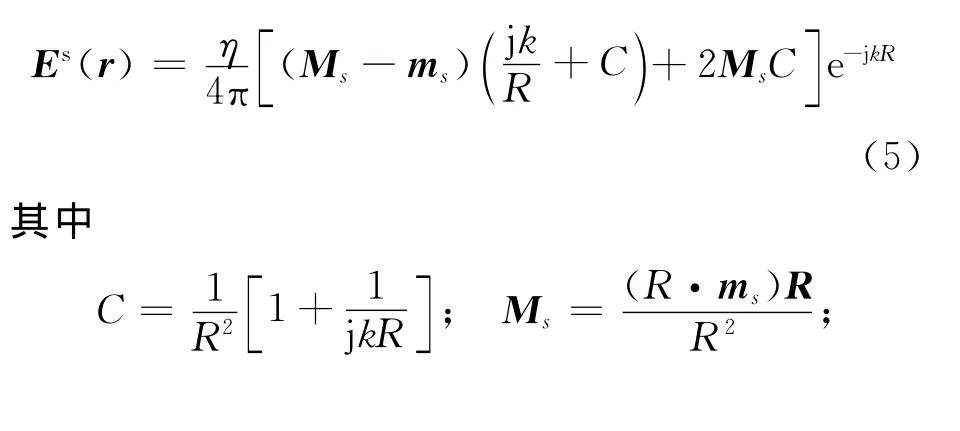
R＝rm－rn为距离矢量；R＝｜R｜；η和k为自由空间的波阻抗和波数。

将（5）式代入（1）式，用权函数fm（r）作用于（1）式两边，并从Es（r）中提出电流系数In可得：

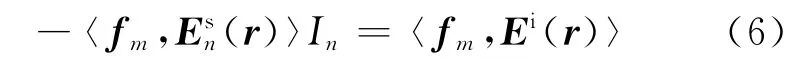
阻抗矩阵元素表达式可由（6）式整理得：

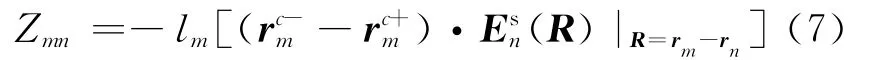
给定频率和入射角，通过（7）式计算出Zmn后代入（3）式求出电流系数In，进而雷达散射截面可由（8）式计算：

其中，u＝uxsinθcosφ＋uysinθsinφ＋uzcosθ，为入射波单位矢量。

数值试验表明当场源距离R＞0.15λ时可运用EDM法加速填充阻抗矩阵元素，不满足此条件，则采用MoM填充。从（7）式可知EDM法的阻抗矩阵元素表达式中没有耗时的积分运算，这正是EDM法显著提高计算效率的主要原因。

1.2 自适应交叉近似算法

自适应交叉近似（ACA）算法具有纯数学理论特性，用于快速计算阻抗矩阵［13］。其原理是将阻抗矩阵分解成尺寸大小不同的子矩阵，通过自适应的方法确定每个子矩阵的秩，尽可能地提取到每个矩阵最小的秩值，从而减少矩阵填充元素，提高计算效率。ACA算法的理论概述如下。

用m×n矩阵Zm×n代表矩量法中远场组的阻抗矩阵。该算法通过2个元素较少的矩阵相乘来构造近似矩阵，并用来近似Zm×n，即

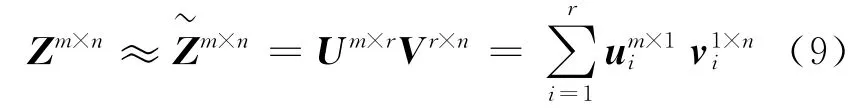
其中，r为矩阵Zm×n的秩；Um×r和Vr×n均是秩为r的满秩矩阵。

误差矩阵Rm×n满足（10）式终止迭代：

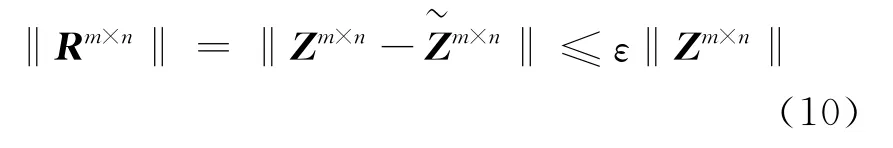
其中，ε为误差迭代门限；‖·‖是矩阵的Frobenus范数。

在实际计算中，秩r≪min（m，n），阻抗矩阵元素由m×n个下降到（m＋n）×r个，运算量明显降低，填充时间大大减少。对近场组，采用MoM结合EDM法加速填充Zm×n。远场作用区域，用ACA算法结合EDM法加速填充抽取行列阻抗矩阵元素。

2 数值结果分析

为了验证本文方法的有效性，分别计算了单缝平板、单缝长方体、三缝隙长方体的双站RCS。所有算 例 均 在 Pentium（R）Dual－Core E6500 2.93 GHz 3.46GB RAM计算机上计算的，编译环境为VC＋＋6.0。算例中入射角度θi＝0°，φi＝0°，垂直于缝隙入射，散射角度θs＝0°～360°，φs＝0°，缝隙尺寸为0.1m×1.0m。采用自重启的最小广义余量迭代法GMRES（m）求解矩阵方程，重启数m＝30，ACA、GMRES（m）误差迭代门限均为0.001。

算例1 计算1.0m×1.5m的单缝理想导体平板的双站RCS。缝隙位于导体平板表面中央，入射频率为1GHz，用三角单元进行剖分，单元数为3 020个，未知量数为4 425，共分割成49个非空组。采用 MoM、EDM 法、EDM－ACA方法计算的单缝导体平板双站RCS如图2所示。由图2可见，3种方法计算结果吻合良好。

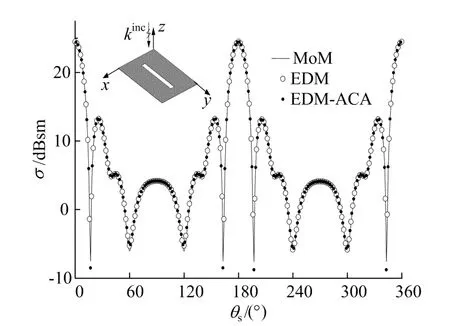
图2 单缝平板的双站RCS

算例2 计算尺寸为2.0m×2.5m×1.0m的单缝理想导体长方体的双站RCS。缝隙位于长方体表面中央，入射频率为350MHz，用三角单元进行剖分，单元数为5 554个，未知变量数为8 331个，共分割成49个非空组。3种方法计算的单缝导体长方体双站RCS曲线如图3所示。由图3可见，3种方法计算结果较为吻合。

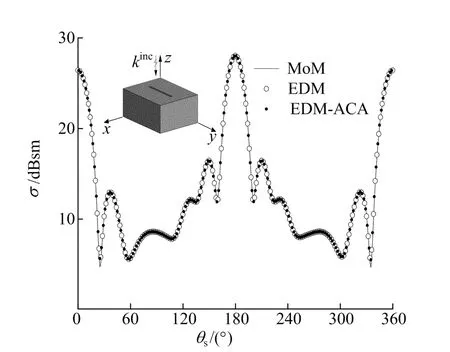
图3 单缝长方体的双站RCS

算例3 计算一个边长为2.0m×2.5m×1.0m的三缝隙理想导体长方体的双站RCS，入射频率为450MHz，采用三角单元剖分长方体，共有10 804个单元，16 206个未知变量，目标被分割成36个非空组。本文方法计算的双站RCS如图4所示，从图4中可以看出，EDM－ACA方法与商业软件FEKO计算结果吻合较好，验证了本文方法在分析复杂开缝导体时也具有较高精度，可移植性好。

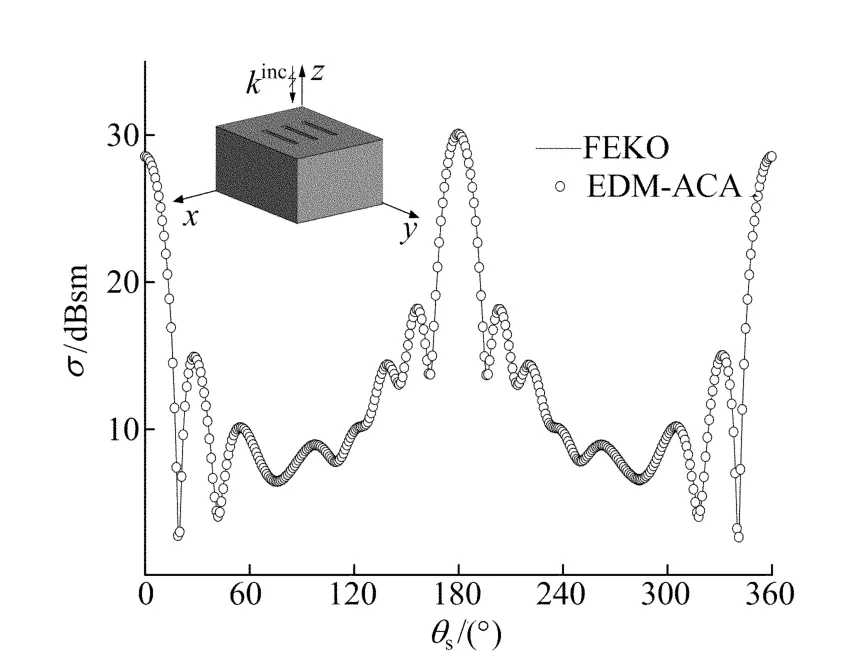
图4 3缝隙长方体的双站RCS

3种算例所消耗的内存、时间见表1所列，从表1可以看出，在同等精度条件下，EDM－ACA方法在节省内存和时间上更具有优势。

表1 3种算例的内存消耗、CPU时间比较

3 结束语

本文将EDM法与ACA算法相结合计算电大开缝导体的RCS。对于近场作用区域采用EDM结合MoM加速填充阻抗矩阵，远场作用区域阻抗矩阵用ACA算法进行压缩，并对抽取的行列阻抗矩阵元素用EDM法加速填充。数值计算结果验证了本文方法的精确性和高效性。此方法还可以推广到其他复杂开缝目标RCS的快速分析中。

［1］阮颖铮.雷达截面与隐身技术［M］.北京：国防工业出版社，1998：1－67.

［2］Senior T，Volakis J.Scattering by gaps and cracks［J］.IEEE Transactions on Antennas and Propagation，1989，37（6）：744－750.

［3］李元新，龙云亮.基于FDTD的微带缝隙漏波天线分析［J］.通信学报，2006，27（1）：81－84.

［4］Song J M，Chew W C.Fast multipole method solution of three dimensional integral equation［C］／／Antennas and Propagation Society International Symposium，Vol 3，1995：1528－1531.

［5］杨立民，张 厚，杨晓荣，等.含有折线型缝隙金属平板散射分析［J］.微波学报，2005，21（Z1）：57－61.

［6］Collins P J，Skinner J P.A hybrid moment method solution for TEz scattering from large planar slot arrays［J］.IEEE Transactions on Antennas and Propagation，2002，50（2）：145－156.

［7］黄沛霖，刘战合.飞行器表面缝隙电磁散射特性研究［J］.航空学报，2008，29（3）：675－680.

［8］刘战合，姬金祖，黄霈霖.用于不连续特征电磁散射计算的新方 法 ［J］.系 统 工 程 与 电 子 技 术，2009，31（8）：1801－1804.

［9］Harrington R F.Field computation by moment methods［M］.New York：McMillan，1968：1－58.

［10］Rao S M，Wilton D R，Glisson A W.Electromagnetic scattering by surfaces of arbitrary shape［J］.IEEE Transactions on Antennas and Propagation，1982，30 （3）：409－418.

［11］Yuan Jiade，Gu Changqing，Han Guodong.Efficient generation of method of moments matrices using equivalent dipole－moment method［J］.IEEE Antennas and Wireless Propagation Letters，2009，8（1）：716－719.

［12］Makarov S N.Antenna and EM modeling with MATLAB［M］.New York：Wiley，2002：30－33.

［13］胡怀宏，孙玉发.一种快速计算阻抗矩阵的有效方法［J］.合肥工业大学学报：自然科学版，2011，34（4）：617－619.