单声道超声流量计不同声道布置形式的流场适应性
郑丹丹,张朋勇,张 涛,赵 丹
(1. 天津市过程检测与控制重点实验室,天津 300072;2. 天津大学电气与自动化工程学院,天津 300072)
单声道超声流量计不同声道布置形式的流场适应性
郑丹丹1,2,张朋勇1,2,张 涛1,2,赵 丹1,2
(1. 天津市过程检测与控制重点实验室,天津 300072;2. 天津大学电气与自动化工程学院,天津 300072)
流量计安装条件对其测量性能的影响是流量测量领域的一个重要问题.基于实流实验与数值仿真相结合方法,对单声道超声流量计的 5种声道布置形式进行研究,对其在 3种典型的阻流件(单弯头、双弯头、渐缩管与单弯头组合)下游的测量性能进行数值仿真,提出了流场敏感误差和流场敏感因子 2个评价指标来表征超声流量计的流场适应性.结果表明:三角形声道布置方式对这 3种非理想流场均有较好的适应性;超声流量计对流场的敏感程度与其声道反射次数没有必然联系,关键是合理布置声道位置.
单声道超声流量计;数值仿真;声道布置;非理想流场
超声流量计近 10年发展迅速,与传统流量计相比,具有无可动部件、管道中无阻挡件、无压力损失、测量范围宽、重复性高等优点,其中最为突出的优点是可用于大管径流量测量,且具有较高的测量精度.但在实际应用过程中,流量计的安装条件直接对其测量性能造成影响.工程现场情况错综复杂,上游弯头、脉动流等都是无法避免的,造成管道中除了沿轴线的流动外,还存在横向流或旋涡流等,这些都是对测量不利的因素.特别对于目前工程中常用的机械结构、测量模型相对简单的单声道超声流量计来说,复杂流场对其测量精度影响更为严重.
国内外学者通过实流实验、数值仿真和理论分析方法[1-2],对单声道超声流量计的流场适应性开展了研究.1990年,Halttunen[3]通过实流实验与数值仿真相结合,对沿径向布置的单声道超声流量计在单弯头和异面双弯头下游的测量性能进行研究,结果表明:在单弯头、双弯头下游 5倍管径(5D)处均会产生约8%的测量误差,随着流量计逐渐远离弯头,测量误差逐渐减小,但即使到了下游 25D处,仍有约 1%的误差;还指出,流量计与弯头相对安装位置不同,测量误差也不同.2000年,Daniel公司基于理论分析方法,对沿径向布置的单声道超声流量计在充分发展理想管流、非对称流以及旋涡流中的测量性能进行分析,指出对于充分发展流动,可以基于流体力学经典湍流速度分布公式进行雷诺数(Re)修正,使测量精度在 1%以内;而对于非对称流和旋涡流,由于无法进行 Re修正,造成测量误差达到 5%以上[4].目前对于充分发展流动,许多学者提出了不同的 Re修正公式[5-8],以提高单声道超声流量计的测量精度.而对于复杂流动,由于不同管件、阻流件下游流场各异,难于用数学模型描述,因此采用数学修正方法提高流量计测量精度十分困难.国内外普遍采用的方法是对声道布置形式进行优化,以提高超声流量计复杂流场的适应性.2001年,美国国家标准与技术研究院(NIST)对单声道超声流量计分别采用直射式和多次反射式的声道布置形式进行比较,指出直射式对横向流动较敏感,而反射式可一定程度上消除横向流动干扰,但对旋涡流较敏感[9].国内学者王明吉等[10-11]基于数值仿真方法,对直射式和多次反射式单声道超声流量计在单弯头和双弯头下游的流场适应性进行研究,指出对于单弯头下游流场,采用多次反射式测量精度较高;而对于双弯头下游流场,直射式声道布置形式更优.此外,清华大学贺胜和彭黎辉等[12]基于计算流体力学仿真,对方形管道中的反射式超声流量计的声道位置进行了优化,取得了良好效果.
综合国内外学者对单声道超声流量计复杂流场的研究成果,笔者基于实流实验与数值仿真相结合方法,对直射式、一次反射、二次反射、三次反射、四次反射共 5种声道布置形式的单声道超声流量计进行系统比较,分别讨论其在单弯头、双弯头以及渐缩管+单弯头3种复杂安装条件下的测量性能,提出表征流量计流场敏感性指标,最终推荐一种较优的单声道布置方案以提高超声流量计的流场适应性.
1 数值仿真方法验证
主要采用数值仿真方法对不同声道布置形式进行对比研究,为了验证仿真方法的可行性,前期开展了实流实验.
1.1 实流实验
实流实验是在天津市过程检测与控制重点实验室的水流量标准装置上完成的,实验管径 100,mm,装置精度 0.1%.将超声流量计置于单弯头下游不同位置,以考察其测量误差.超声流量计选用 GE公司的 AF878管段式超声流量计(如图 1所示),口径DN100.该样机采用时差法进行测量,包含 2对传感器,每对传感器所发射的超声信号在管道内壁上经过一次反射,被对应的传感器接收,形成一条“一次反射”声道,也称“V”型声道.2对探头共形成 2条“V”型声道,均经过管道轴心,且 2条“V”型声道所在平面互相垂直(如图2所示).2条声道的声路角均为45°,声道1的旋转角为45°,声道2的旋转角为-45°(或 315°),流量计与单弯头的相对安装位置如图3所示.

图1 AF878超声流量计Fig.1 Ultrasonic flowmeter AF878

图2 AF878声道布置Fig.2 Acoustic path arrangement of AF878

图3 实流实验管道安装Fig.3 Layout of flow experimental setup
实验共测试了单弯头下游4个位置,均以管道直径D作为最小基本单位.每个位置测试8个流量点,测量结果如图4所示.
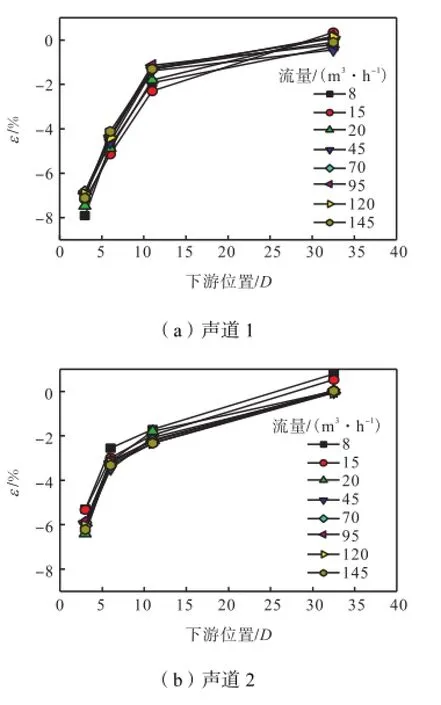
图4 单弯头下游各位置流量测量误差Fig.4 Measurement errors of each position downstream of single elbow
图4分别给出了利用声道1和声道2进行测量时,超声流量计测量误差随安装位置的变化曲线.ε表示超声流量计的测量误差,其计算式为

式中:Q为超声流量计测量值;sQ为标准表流量值.
1.2 仿真方法
基于 Fluent仿真软件对上述实流实验进行数值仿真,仿真模型如图5所示.单弯头的弯径比为1.5,弯头上游直管段长 24.5D,下游直管段长 50D.管壁粗糙度为 1,mm.采用六面体网格对模型进行剖分,湍流模型选用RSM模型,残差收敛精度为10-6.

图5 单弯头仿真模型Fig.5 Simulation model of single elbow
超声流量计的测量原理是通过测量时差来反映各声道上的线平均流速,进而基于 Re修正得到面平均流速,从而获得流量.由于Fluent仿真方法无法引入声波传播时间,因此对于各声道线平均流速的计算采用对声道上各弦线节点速度进行线积分的方法.假设声道中任意一条弦线AB如图6所示,与x、y、z轴向正方向夹角分别为α β γ、 、 ,则 AB上的流速线积分为

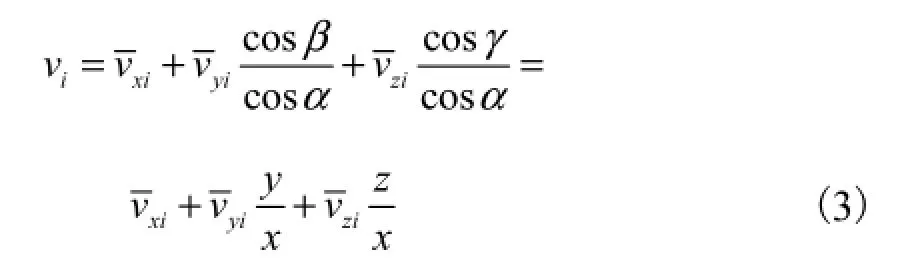

式中n为声道上包含弦线数量,如一次反射式包含2条弦线,n=2.
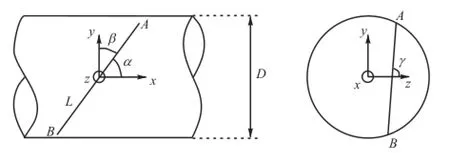
图6 弦线位置示意Fig.6 Schematic of segment position
1.3 仿真与实流对比
基于上述仿真方法,对实流实验工况进行数值仿真,结果如图7所示.图7中:E表示实流实验,S表示仿真.例如,E-32.5D表示单弯头下游 32.5D处实流实验获得的测量误差.
由对比可知:仿真测量误差和实验测量误差拥有相同变化规律,即随超声流量计安装远离弯头,测量误差逐渐偏负,且误差绝对值逐渐增大;声道 1的仿真结果与实验结果相差较小,两者最大相差约为1%;声道2的仿真结果与实验相差稍大,最大相差约2%.

图7 仿真与实流实验测量误差对比Fig.7 Comparison of measurement errors between numerical simulation and experiments
造成这一偏差的原因主要是几何建模和参数设置不可能与实流实验完全一致.此外,数值仿真方法本身也存在一定的系统误差.但从整体对比结果看,利用仿真方法能够有效复现测量误差的变化规律,因此基于仿真方法研究不同声道布置形式时单声道超声流量计的流场适应性是可行的.
2 不同声道布置形式流场适应性对比
2.1 对比内容
基于 Fluent数值仿真方法,对 5种声道布置形式的单声道超声流量计在 3种典型工况下的测量性能进行对比研究.
图 8所示为不同声道布置形式,分别为直射式(径向型)、一次反射(V型)、二次反射(三角形)、三次反射(正方形)和四次反射(五角星形)式.其中,定义声路角为各声道弦线与管道轴线 x方向的夹角,5种声道布置形式的声路角均为45°.由于反射式声道布置形式由多段弦线组成,因此定义旋转角为最靠近上游弦线与 Oxz平面的夹角,V型布置旋转角为135°,其他4种声道布置旋转角均为0°.
为了说明各声道布置形式与阻流件的相对安装位置,图9给出了径向型超声流量计与3种阻流件的安装示意,阻流件分别为单弯头、同一平面双弯头以及渐缩管+单弯头.其余 4种流量计的安装方向与径向型相同.
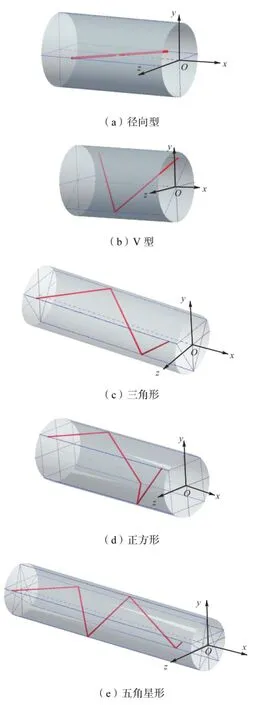
图8 5种声道布置形式Fig.8 Five types of acoustic path arrangements

图9 流量计与阻流件安装位置示意Fig.9 Relative installation position of flowmeter and pipe fittings
2.2 评价指标
为比较不同声道布置形式对复杂流场的适应性,提出了2个评价指标.
测量误差(见式(1))是评判流量计测量性能好坏的重要指标.当流量计置于复杂流场中,其测量误差势必会发生变化.为比较不同声道布置形式超声流量计的流场适应能力,针对每种声道布置形式,选择阻流件下游各位置处测量误差绝对值最大值作为该
2) 流场敏感因子Sens
较好的流场适应性还应体现在,当流量计安装于阻流件下游的不同位置时,其仪表系数K稳定,不随安装位置的改变而波动,即流量计对阻流件下游流态变化不敏感.若满足这一条件,按照仪表出厂时充分发展管流下的测量结果进行仪表系数修正后,流量计处于该阻流件下游的任何位置仍能保证较高精度.K的计算式为

流场敏感因子计算式为

式中maxK 、minK 分别表示阻流件下游不同位置处仪表系数的最大值和最小值.
流场敏感因子是评价流量计在阻流件下游对其流场的适应能力.Sens越小,表示流量计对该流场流态变化越不敏感,即对该阻流件的流场适应能力越强.
2.3 流场适应性对比分析
以下将分别对 3种阻流件下游 5种不同声道布置形式的超声流量计进行研究,通过对比文中提出的2个评价指标,优选出流场适应性较好的声道布置形式.
本文第1.3节的实流实验与仿真结果(见图7)均表明,超声流量计测量误差基本不随流量变化而变化,呈较稳定的趋势.因此,在这部分研究中选取一个典型流量点 45,m3/h进行数值仿真研究,重点讨论超声流量计在阻流件下游 5个位置 2D、5D、10D、20D和 30D处的流场适应性.流量计与阻流件安装相对位置如图9所示.
1) 单弯头
图 10、图 11分别为不同声道布置形式测量误差、仪表系数随下游位置变化曲线.表 1为单弯头情况时流场敏感误差计算结果,表2为流场敏感因子计算结果,5种声道布置形式如图8所示.

图10 测量误差变化曲线Fig.10 Change curves of measurement error

图11 仪表系数变化曲线Fig.11 Change curves of meter factor
测量误差和仪表系数的变化反映的都是超声流量计的测量性能,两者是相辅相成的.当 0ε< 时,K>1;当ε>0时,K<1.因此,通过对图10和图11分析可以得到:除了三角形声道形式外,其余 4种声道布置的超声流量计测量误差(或仪表系数)均随下游安装位置变化较大.越靠近单弯头,测量误差越大.其中,径向型、V型和正方形在下游2D处误差达到 10%以上(见表 1).五角星形测量性能稍好,但也达到了 7%.只有三角形超声流量计的测量误差随下游安装位置变化较平缓,且测量误差较小,各位置均在2%以内.
进一步分析前述提出的表征流量计流场适应性的 2个评价指标.如表 1、表 2所示,三角形声道布置形式不仅流场敏感误差最小,而且其流场敏感因子也最小.综合 2个评价指标,采用三角形声道布置形式的超声流量计流场适应性最好,径向型声道布置形式的流场适应性最差.
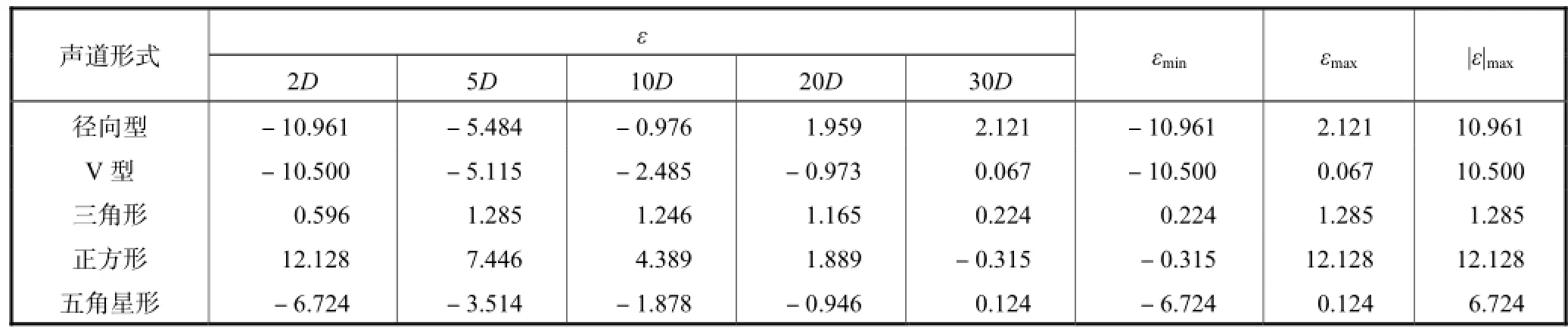
表1 单弯头情况时流场敏感误差Tab.1 Flow-sensitive errors of single elbow %

表2 单弯头情况时流场敏感因子Tab.2 Flow-sensitive factors of single elbow
此外,从比较结果来看,超声流量计的流场适应性与声道反射次数没有必然联系,不一定反射次数越多,声道越长,其流场适应性越好.为验证这一结论,对其他2种阻流件工况开展了相同的研究工作.
2) 双弯头
表3为双弯头情况时流场敏感误差计算结果,表4为流场敏感因子计算结果.

表3 双弯头情况时流场敏感误差Tab.3 Flow-sensitive errors of double elbows %

表4 双弯头情况时流场敏感因子Tab.4 Flow-sensitive factors of double elbows
从比较结果看,双弯头情况时三角形声道布置优势明显,流场敏感误差和流场敏感因子均为5种声道布置中最小.与单弯头相比,三角形布置方案对双弯头下游流场更不敏感,测量性能更佳.综合 2个指标看,径向型和正方形声道布置对双弯头下游流场的适应性最差.
3) 渐缩管+单弯头
表 5为渐缩管+单弯头情况时流场敏感误差计算结果,表6为流场敏感因子计算结果.

表5 渐缩管+单弯头情况时流场敏感误差Tab.5 Flow-sensitive errors of reducer and single elbow %

表6 渐缩管+单弯头情况时流场敏感因子Tab.6 Flow-sensitive factors of reducer and single elbow
从比较结果看,渐缩管+单弯头情况时三角形声道布置对流场的适应性仍旧最好;而 V型和正方形声道布置的流场适应性最差.同时,也再次验证了声道反射次数与提高超声流量计流场适应性没有必然联系.
3 结 语
采用计算流体动力学仿真方法对单声道超声流量计流场适应性进行了研究,对比分析了径向型、V型、三角形、正方形和五角星形 5种声道布置形式的超声流量计在单弯头、双弯头、渐缩管+单弯头 3种阻流件下游的测量性能,提出了评价超声流量计流场适应性的 2个指标,即流场敏感误差和流场敏感因子.分析表明:在管道内经过二次反射的三角形超声流量计对多种复杂流场均有较好的适应性,即在能保证一定测量精度的前提下,三角形超声流量计所需的前直管段可以更短,适用范围更宽;超声流量计对各种流场的敏感程度与其声道反射次数没有必然联系,合理布置声道位置才是提高流量计流场适应性的关键.
[1] Barton N A,Boam D. In-Service Performance of Ultrasonic Flowmeters—Application and Validation of CFD Modeling Methods[R]. London:National Measurement System Directorate,2002.
[2] Zanker K J. The effects of Reynolds number,wallroughness, and profile asymmetry on single-and multipath ultrasonic meters [C]// North Sea Flow Measurement Workshop. Oslo,Norway,1999:25-28.
[3] Halttunen J. Installation effects on ultrasonic and electromagnetic flowmeters:A model-based approach [J]. Flow Measurement and Instrumentation,1990,1(10):287-292.
[4] Zanker K J. Installation effects on single and multi-path ultrasonic meters [C]// FLOMEKO 2000,10th Conference on Flow Measurement. Salvador,Brazil,2000:4-8.
[5] Lynnworth L C,Liu Yi. Ultrasonic flowmeters: Halfcentury progress report,1955-2005[J]. Ultrasonics,2006,44(12):1371-1378.
[6] Luscher B,Staubli T,Tresch T,et al. Optimizing the acoustic discharge measurement for rectangular conduits[C]// 7th International Conference on Hydraulic Efficiency Measurements. Milano,Italy,2008:3-6.
[7] Moore P I,Brown G J,Stimpson B P. Ultrasonic transit-time flowmeters modeled with theoretical velocity profiles:Methodology[J]. Measurement Science and Technology,2000,11:1802-1811.
[8] 李跃忠,李昌禧. 高精度超声流量传感器建模[J]. 传感器技术,2005,24(11):24-26.
Li Yuezhong,Li Changxi. Modeling of high accuracy ultrasonic flow sensor [J]. Journal of Transducer Technology,2005,24(11):24-26(in Chinese).
[9] Yeh T T,Espina P I. Special ultrasonic flowmeters for in-situ diagnosis of swirl and cross flow [C]// Proceedings of ASME Fluids Engineering Division Summer Meeting. New Orleans,USA,2001:29.
[10] 王明吉,周 围. 单声道超声流量计在单弯管流场中的适应性研究[J]. 工业计量,2007,17(6):1-4.
Wang Mingji,Zhou Wei. Study on adaptability of single acoustic path ultrasonic flowmeter in single bending pipe flow field [J]. Industrial Measurement,2007,17(6):1-4 (in Chinese).
[11] 王明吉,周 围. 单声道超声流量计在双弯管流场中的适应性研究[J]. 计量技术,2007(10):6-8.
Wang Mingji,Zhou Wei. Study on adaptability of single acoustic path ultrasonic flowmeter in double elbows pipe flow field [J]. Measurement Technology,2007(10):6-8 (in Chinese).
[12] 贺 胜,彭黎辉,仲里敏. 基于CFD的超声波流量计最优声道位置研究[J]. 仪器仪表学报,2009,30 (4):852-856.
He Sheng,Peng Lihui,Zhong Limin. Computational fluid dynamics based sound path optimization for ultrasonic flowmeter [J]. Chinese Journal of Scientific Instrument,2009,30(4):852-856(in Chinese).
(责任编辑:田 军)
Flow Adaptabilities of Single-Beam Ultrasonic Flowmeters with Different Acoustic Path Arrangements
Zheng Dandan1,2,Zhang Pengyong1,2,Zhang Tao1,2,Zhao Dan1,2
(1. Tianjin Key Laboratory of Process Measurement and Control,Tianjin 300072,China;2. School of Electrical Engineering and Automation,Tianjin University,Tianjin 300072,China)
Installation effects of flowmeters on their performances have been recognized as a major problem in flow measurements. Single-beam ultrasonic flowmeters with five different types of acoustic path arrangements were investigated based on experiments and numerical simulations in this paper. Measurement performances of these flowmeters downstream of three typical installation conditions,single elbow,double elbows and reducer and single elbow,were mainly numerical simulated and discussed. In order to compare flow adaptabilities of the five types of flowmeters for three non-ideal flow fields,two evaluation parameters were proposed:flow-sensitive error and flowsensitive factor. Results show that the best flow adaptability can be obtained from the triangle type of ultrasonic flowmeter under complex installation conditions. Besides,instead of increasing the number of sound path reflections,the key factor to improve the non-ideal flow adaptability of single-beam ultrasonic flowmeter is to arrange the acoustic path appropriately.
single-beam ultrasonic flowmeter;numerical simulation;acoustic path arrangement;non-ideal flow field
TP212.9
A
0493-2137(2014)08-0703-08
10.11784/tdxbz201211026
2012-11-14;
2012-12-15.
国家自然科学基金青年基金资助项目(61101227);天津市应用基础与前沿技术研究计划资助项目(13JCQNJC03300).
郑丹丹(1981— ),女,博士,副教授.
郑丹丹,zhengdandan@tju.edu.cn.

