基于模糊多属性群决策的经纱张力检测及控制方案优选

倪敏娜，李 萍，李 艳

（1.东华大学 机械工程学院，上海 201620；2.陕西职业技术学院 管理系，陕西 西安 710100）

基于模糊多属性群决策的经纱张力检测及控制方案优选

倪敏娜1，李 萍2，李 艳1

（1.东华大学 机械工程学院，上海 201620；2.陕西职业技术学院 管理系，陕西 西安 710100）

针对剑杆织机经纱张力检测及控制方案设计的评价要求，提出工程方案评价的模糊多属性群决策问题.考虑了个体专家在方案属性中的不同重要程度，将专家个体意见与群体相似度结合，计算专家意见的综合重要程度.通过专家意见集结，得到群体意见决策矩阵.利用模糊逼近理想解（TOPSIS）决策法和三角模糊数计算各方案与正负理想方案的距离以及各方案与理想点的相对接近度，确定经纱张力检测及控制最优方案.决策结果验证了该方法的可行性和有效性.

模糊多属性群决策；经纱张力检测及控制；方案优选；综合权重

经纱张力是织物织造过程中的重要参数，对织机成布质量有至关重要的影响.在织造过程中，随着四大机构运动的不断重复进行，经纱张力受到诸多因素的影响，在回转周期的不同时刻发生不同的变化.经纱张力检测及控制是织机控制系统的重点和难点问题，其方案决策与优选具有积极的理论意义和实用价值［1］.模糊多属性群决策理论与方法是求解工程方案决策与优选的有效途径［2］，其通过模糊语言描述备选方案及其属性建立群决策矩阵，并利用模糊决策理论求解决策问题.模糊多属性群决策的处理方法如模糊逼近理想解（TOPSIS）法、模糊层次分析（AHP）法、模糊德尔菲（Delphi）法及其综合应用等［3-4］，是解决多属性群决策问题的热门方法.群决策理论与方法被广泛应用于供应商评价、企业绩效评价、社会经济决策等领域［5］，但很少用于生产及工程决策，尤其是工程设计方案的评价与优选.为此，本文采用基于TOPSIS的模糊多属性群决策方法，解决经纱张力检测及控制方案的评价和优选问题，拟将为工程设计方案评价提供理论支持.

1 经纱张力检测及控制系统的设计方案及其评价因素

经纱张力检测及控制系统设计因素较多，包括硬件设备、设计参数以及控制策略、程序设计等，而控制系统的评价则从功能、性能和成本等因素出发，给出评价准则.

1.1 控制系统的工程设计方案

经纱张力检测及控制方案具体内容如表1所示.其中，控制方案由系统硬件（试验电路设计方案）和系统软件（控制策略、算法和参数计算）组成［1，6］.

表1 经纱张力检测及控制系统组成Table 1 Schemes composition of warp tension measurement and control system

1.2 评价设计方案的主要因素

在工程应用中评定经纱张力检测及控制的主要指标应具有实时性和快速性好、精确度和灵敏度高、抗干扰能力强等，具体如下所述.

（1）实时性和快速性.检测机构应快速检测经纱运动中的动态张力，信号处理电路实时放大和转换张力信号，控制算法应快速响应和实时处理，电机及其驱动器应及时响应软件指令等.

（2）精确度和灵敏度.如经纱动态张力检测元件及信号转换元件的精确度、电路参数灵敏度及其误差范围、硬件元器件对误差信号的灵敏度、控制算法的精确度以及系统输出控制的准确度等.

（3）抗干扰及补偿能力.织机在运行过程中，各机构运动、经轴直径、织造中纬密以及目标张力的变化都会影响经纱张力变化，造成稀密路.在织机开停车时，造成织物停车痕.系统设计应分析影响经纱张力的扰动因素，通过设计控制模块或算法，及时补偿张力扰动，提高张力的响应和精度，降低超调量.

此外，经纱张力检测与控制还包括其他评价因素，如系统稳定性、可靠性、开发及运行成本等，因涉及后期加工调试等诸多因素，在设计方案筛选阶段无法预估，故本文暂不做考虑.

由以上分析可知，经纱张力检测与控制的评价因素包括定量指标和定性指标.如在快速性和实时性评价因素中，定量指标包括放大倍数、运行时间、误差系数等数值指标，这些指标的数值单位也不同；定性指标包括主控电路的实时处理能力和控制算法优化程度等，一般通过语言值如“好”“较好”“一般”等评价.

由多种评价因素组成的决策问题可能存在某些指标相互矛盾的情况，如系统快速响应和稳定时间、精确度与稳定性之间等，采用传统决策方法很难得到最优化处理.另外，在表1所示的备选方案组成中，因设计师的客观条件和主观经验所限可能存在不完整信息.模糊多属性群决策能有效处理这些模糊和不明确信息，并获得满意解.

2 TOPSIS和模糊多属性群决策方法

2.1 模糊多属性群决策问题描述

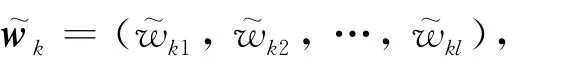
2.2 专家群对方案属性-权重信息的集结

根据专家在各方案下对不同属性的取值，得到各方案决策矩阵如式（1）所示.

其中：为专家c k对方案x i中属性u j的模糊评价值，用三角模糊数表示，其定义为

其中：aL，aM和aU分别表示三角模糊数a～（x）的下界、中值和上界.

将各方案的属性评价信息与权重信息集结，得到加权决策矩阵如式（2）所示.

2.3 专家综合重要程度确定

本文在考虑专家个人主观意见的同时，引入专家意见相似度的概念，即既尊重专家的个体权威，也考虑专家个体在专家群体中的重要程度，将专家个人意见的主观性和专家群意见相似度的客观性相结合，给出专家意见的综合重要程度（权重）.为考虑不同专家在不同方案同一属性下的评价值的相似度，将决策矩阵转换为属性矩阵如式（3）所示.

其中：为属性u j下专家c k对方案x i的模糊评价值，即属性矩阵为同一属性u j下各专家对各方案的评价值.

（1）由三角模糊数相似度定义，可得在相同主观评价属性uj∈U下，任意两个专家个体ck和c z对同一方案x i的评价值用三角模糊数表示为

其评价值相似度可表示为

专家个体ck和c z对所有方案在属性u j下的相似度表示为

（2）计算专家ck在全部方案同一属性u j下的评价值在专家群体中的平均相似度

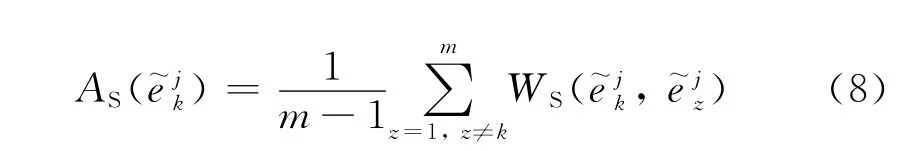
（3）计算专家ck在全部方案的同一属性u j下的评价值在专家群体中的相对相似度

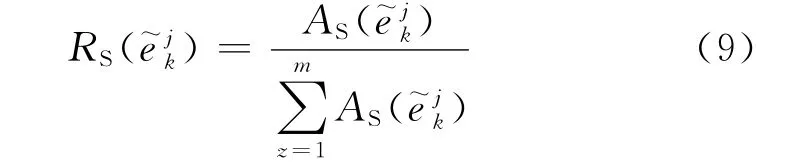
（4）综合专家个体权威以及专家个体意见与专家群体意见的相似度，得到专家ck在属性u j下综合重要程度（专家综合权重）为

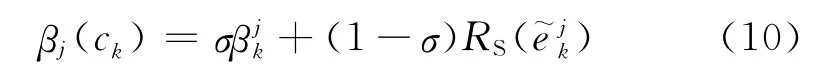
其中：σ为主客观权重因子，一般取0.5.

2.4 专家意见的集结

对若干专家个体关于方案在主观评价属性下的评价值进行集结，并在集结过程中考虑专家个体在专家群体中的综合重要程度.

根据模糊集理论的扩展原理，专家群的规范化综合模糊决策矩阵为

其中：为专家群关于方案x i在属性u j下的评价值，表示为

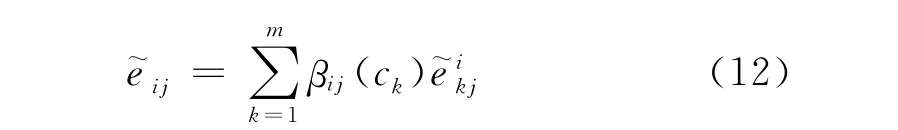
由式（12）可获得专家群体对各方案的属性评价值集合.

2.5 利用TOPSIS方法求多属性决策问题

在专家群综合模糊决策矩阵确定之后，采用TOPSIS［6］方法求解多属性决策问题，并获得最优方案.

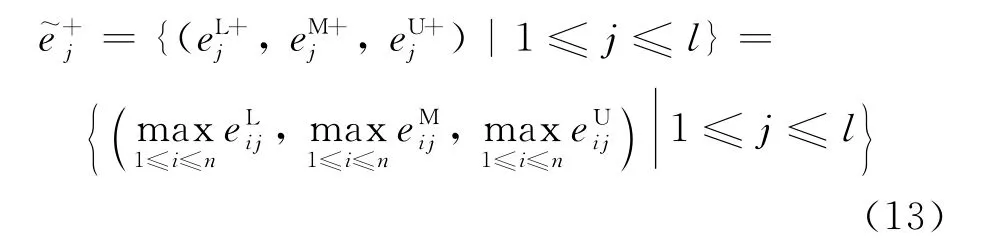
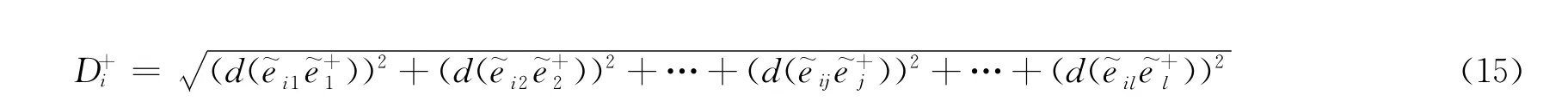
（2）计算各方案与正负理想解的距离.利用三角模糊数的距离式，可得方案x i与正理想解（方案）的距离为

其中：

方案x i与负理想解（方案）的距离计算式与上述类似，不再赘述.

（3）计算各方案与正负理想解的相对接近度.最优方案不但要尽量接近正理想方案，而且要尽量远离负理想方案.方案xi与理想方案的相对接近度L（xi）由式（17）表示.相对接近度越大，相应的方案越优.

（4）根据取值大小选择多属性决策问题的最优方案.将各方案按相对接近度L（x i）由大到小排列，取值最大的方案即为多属性决策问题的最优方案.

3 纱线张力检测及控制方案评价

某型号高速刚性剑杆织机，织机设计车速为750 r／min，引纬率为1 300 m／min，筘幅为460 cm，多臂机开口，16色选纬装置，要求针对表2所示的3种经纱张力检测及控制方案进行评价并选出最佳方案.具体设计包括张力检测及处理、电机驱动方式、主轴转速检测、控制策略与算法、张力补偿、可靠性设计.

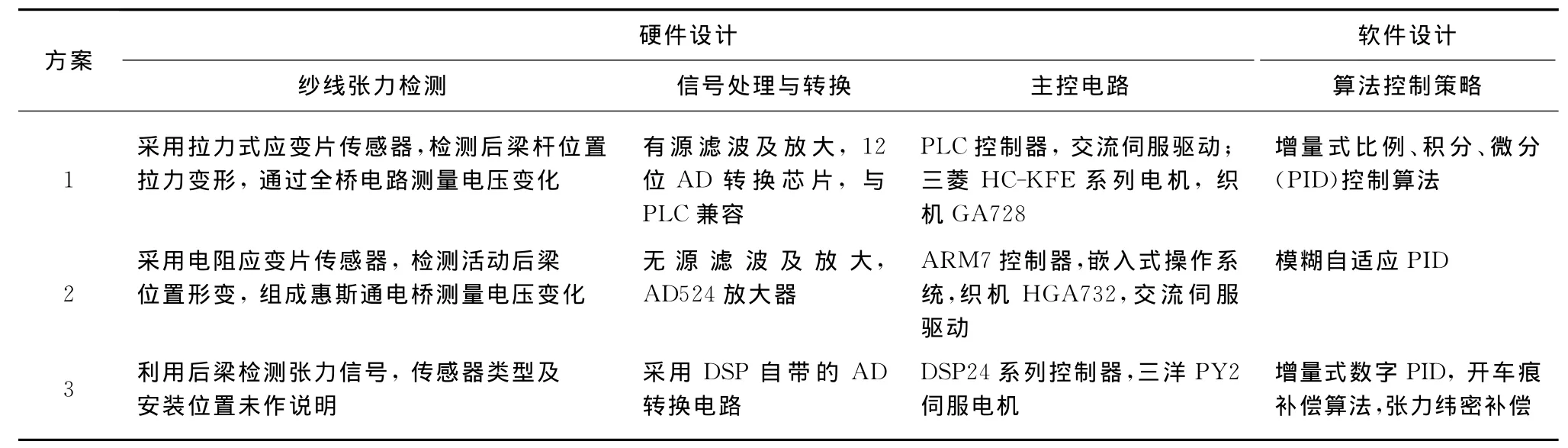
表2 3种纱线张力检测及控制系统设计方案Table 2 Design schemes of three warp tension measurement and control systems

根据前述3种高速剑杆织机电子送经卷取控制系统方案评价要求，由3位相关专业技术专家c1，c2，c3组成决策群体，制定了3种功能型评价指标，包括实时性与快速性u1、精确度与灵敏度u2、干扰补偿能力u3.对各评价属性的定性和定量指标，由决策群采用统一语言值处理.设定专家个体的评价权重相同，即βj＝（1／3，1／3，1／3）.使用相同粒度的语言评价集，其语言短语与三角模糊数的对应关系如表3所示.

表3 语言短语与三角模糊数的对应关系Table 3 Correspondences between language phrases and triangle fuzzy data

（1）根据表2中方案分析，专家c1，c2，c3给出的属性权重向量和方案决策矩阵分别为

（2）将各方案的属性评价信息与权重信息集结，得到决策矩阵为

（3）计算专家综合重要程度.由式（3）～（6）计算3位专家同一属性u1下的评价值在专家群体中的平均相似度，再根据式（7）计算3位专家在专家群体中的相对相似度.利用式（8）得到各专家在各属性下的综合权重为

（4）对专家意见进行集结.根据式（11）和（12），得到综合模糊评价矩阵为

（5）根据式（13）和（14），得到正负理想矩阵为

（6）根据式（15）和（16），计算各方案与正负理想矩阵的距离为

（7）根据式 （17），计算各方案关于理想解的相对接近度为

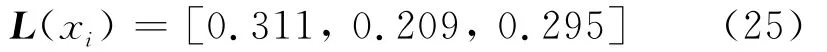
（8）根据相对接近度大小，得出优选方案.由各方案关于理想解的相对接近度可看出，方案1最优，方案3次之，方案2最差.更具体地，由式（22）所表示的模糊综合矩阵，其物理意义为各方案的属性评价集，从数值上看，方案2在各属性上得分相对较低，方案1和3在属性1和2上差异不大，而在属性3上差值较大，因此，方案1相对更优.

4 结 语

本文提出一种模糊多属性群决策方法用于纱线张力检测及控制系统方案的评价与优选.决策方法利用意见相似度概念获得决策者的客观权重，在考虑决策者的主观意见及其在群体中重要度的基础上，计算了决策者的综合权重.进一步获得备选方案的模糊综合决策矩阵，利用模糊决策方法和TOPSIS方法求解模糊综合决策矩阵，并获得各备选方案的评价值，最后得到优选方案.通过评价结果分析，验证了本文方法可以为工程设计方案评价提供理论依据和数学支持，具有一定的应用价值.

［1］周其洪.新型高速织机的关键控制技术研究［D］.上海：上海大学机电工程与自动化学院，2008：205-209.

［2］ERAH B，OKAN D，TUBA K，et al.Use of consistency index，expert prioritization and direct numerical inputs for generic fuzzy-AHP modeling：A process model for shipping asset management［J］.Expert Systems with Applications，2012，39（2）：1911-1923.

［3］刘源，王丙祥，李琳.基于TOPSIS的模糊群体多属性决策方法［J］.数学的实践与认识，2012，42（11）：107-113.

［4］JOSHI R，BANWET D K，SHANKAR R.A Delphi-AHPTOPSIS based benchmarking framework for performance improvement of a cold chain［J］.Expert Systems with Applications，2011，38（8）：10170-10182.

［5］施广军.剑杆织机纱线张力电子检测与控制技术研究［D］.上海：东华大学机械工程学院，2012：356-380.

［6］VAHDANI B，MOUSAVI S M，MOGHADDAM R T.Group decision making based on novel fuzzy modified TOPSIS method［J］.Applied Mathematical Modelling，2011，35（9）：4257-4269.

Schemes Selection of Warp Tension Measurement and Control Based on Fuzzy Multiple-Attribute Group Decision Making

NIMin-na1，LIPing2，LIYan1

（1.College of Mechanical Engineering，Donghua University，Shanghai 201620，China；2.Management Department，Shaanxi Vocational ＆Technical College，Xi'an Shaanxi 710100，China）

The schemes evaluation problems are proposed for warp tension measurement and control schemes in rapier looms.A fuzzy multiple-attribute group decision making method is proposed for the design schemes evaluation.Firstly，important degrees of every attributes from each expert are considered.The individual opinions of each expert are integrated with the similarity of the decision group.And the comprehensive weights of each expert are calculated.Secondly，with the aggregation of experts'opinions，the group attribute-weights matrixes are obtained.Then the TOPSIS（technique for order preference by similarity to an ideal solution）and triangular fuzzy numbers are used to sequence the schemes，and the optimal scheme is decided for warp tension measurement and control system，the decision results illustrate the feasibility and effectiveness of the developed method.

fuzzy multiple-attribute group decision making；warp tension measurement and control；schemes selection；comprehensive weights

C 934；TP 23

A

2012-12-31

倪敏娜（1977—），女，浙江余姚人，讲师，硕士，研究方向为设计管理.E-mail：nimn＠dhu.edu.cn

李 艳（联系人），女，副教授，E-mail：liyanly＠dhu.edu.cn

1671-0444（2014）03-0282-06